基于减法平均算法的无人机航迹规划-附代码
基于减法平均算法的无人机航迹规划
文章目录
- 基于减法平均算法的无人机航迹规划
- 1.减法平均搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用减法平均算法来优化无人机航迹规划。
1.减法平均搜索算法
减法平均算法原理请参考:https://blog.csdn.net/u011835903/article/details/130542885
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得减法平均搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用减法平均算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,减法平均算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于减法平均算法的无人机航迹规划-附代码
基于减法平均算法的无人机航迹规划 文章目录 基于减法平均算法的无人机航迹规划1.减法平均搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用减法平均算法来优化无人机航迹规划。 …...

C语言--每日五道选择题--Day4
第一题 1、如果 x2014 ,下面函数的返回值是( ) int fun(unsigned int x) {int n 0;while(x 1){n;x x | (x 1);}return n; } A: 20 B: 21 C: 23 D: 25 答案及解析 C 这个函数的作用是对整型中0的个数进行统计 x x | (x1) 的作用是每次…...

OpenCV图片验证码识别与滑块验证码识别
目录 图片验证码识别: 一、百度OCR文字识别云服务 二、维普网获取图片验证码 三、维普网opencvocr识别验证码 四、维普网selenium登录并获取数据 滑块验证码: 五、猎聘网获取滑块验证码 六、猎聘网opencv计算滑动距离 七、猎聘网selenium模拟滑…...
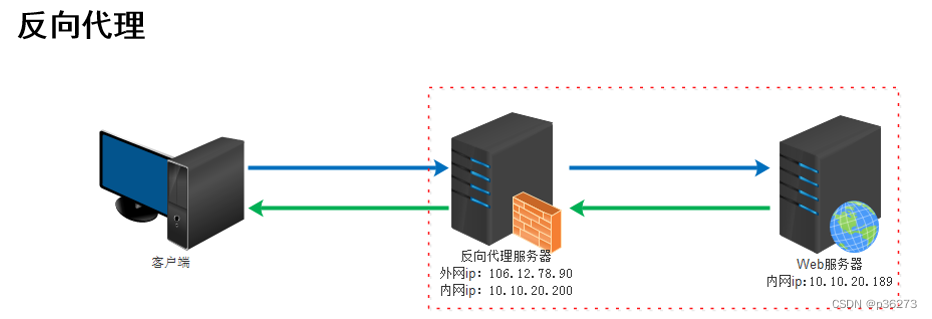
网络安全深入学习第八课——代理与端口转发
文章目录 一、什么是代理二、正向代理三、反向代理四、正向和反向代理模拟复现 一、什么是代理 代理服务器英文全称是Proxy Server,其功能就是代理网络用户去取得网络信息。 形象的说:它是网络信息的中转站。在一般情况下,我们使用网络浏览…...

11月7日,每日信息差
今天是2023年11月07日,以下是为您准备的17条信息差 第一、五粮液否认内部讨论提价传闻 第二、雷军证实小米14销量已超百万台 第三、支付宝生活号全面开放UGC入口。据了解,今年以来,支付宝生活号陆续上线了创作者中心、热点榜单等多个内容产…...

sql异常Encountered unexpected token BINARY
1.出现错误 2023-11-06 10:48:19.604 [http-nio-8091-exec-3] WARN c.b.m.e.p.i.PaginationInnerInterceptor - [autoCountSql,343] - [e322891e-de87-4d98-8456-f6448d3c165e] - optimize this sql to a count sql has exception, sql:"selects.id,s.command,s.catego…...

P1131 [ZJOI2007] 时态同步
Portal. 先找出树上以 S S S 为起点最长的一条链,然后让其他链的长度都和该链对齐即可。 维护每个结点 x x x 的子树最长链 d max ( x ) d_{\max}(x) dmax(x),则每次 DFS 求出最长链之后调整对齐的代价为 d max ( x ) − ( d max ( s o …...
)
springboot(ssm 旅游管理系统 旅游规划平台 Java(codeLW)
springboot(ssm 旅游管理系统 旅游规划平台 Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0ÿ…...

C++ 构造函数不能是虚函数的原因
构造函数不能被声明为虚函数的主要原因涉及到对象的创建和初始化过程以及虚函数的工作机制。下面详细解释为什么构造函数不能是虚函数: 1.构造函数的调用顺序: 构造函数用于创建对象,并且对象的构造是在派生类构造函数之前完成的。当你创建…...
【LearnOpenGL基础入门——2】搭建第一个OpenGL窗口
目录 一.配置GLFW 二.配置GLAD 三.第一个OpenGL窗口 3.1 GLFW设置 3.2 GLAD设置 3.3 视口 3.4 输入 3.5渲染 在我们画出出色的效果之前,首先要做的就是创建一个OpenGL上下文(Context)和一个用于显示的窗口。然而,这些操作在每个系统上都是不一样…...
第三章:人工智能深度学习教程-人工智能与机器学习与深度学习之间的区别
人工智能基本上是通过一组规则(算法)将人类智能融入机器的机制。人工智能是两个词的组合:“人工”是指由人类或非自然物体制造的东西,“智能”是指相应地理解或思考的能力。另一个定义可能是“人工智能基本上是训练机器࿰…...
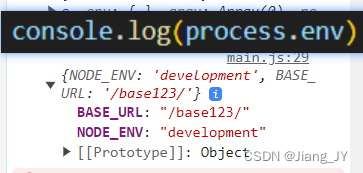
vue中 process.env 对象为空对象问题
问题:今天在处理vue项目环境问题的时候,发现直接打印 process 对象和打印 process.env 时 env 对象输出结果是不一样的,如下图所示: 在网上搜索了一番后发现还是有挺多朋友对此感到疑惑的,询问了同事,同…...

uniapp小程序v-for提示“不支持循环数据”
问题描述: 在uniapp小程序项目中使用多层for循环时,小程序端提示:uniapp v-for 暂不支持循环数据,以至于获取不到循环的数据。 <view v-for"(item,index) in list" :key"item.id"> <view v-for"child i…...

CROS错误 403 preflight 预检
预检 403 响应 Response for preflight 403 forbidden 如上图,配置了请求接口一直报错,前端看了没有什么问题,不知道哪里报错了,那么可能是后端没有设置跨域。(或者是设置了,但是可能需要换一种方式&#…...

nginx参数调优能提升多少性能
前言 nginx安装后一般都会进行参数优化,网上找找也有很多相关文章,但是这些参数优化对Nginx性能会有多大影响?为此我做个简单的实验测试下这些参数能提升多少性能。 声明一下,测试流程比较简单,后端服务也很简单&…...
用友U8 Cloud 反序列化RCE漏洞复现
0x01 产品简介 用友U8 Cloud是用友推出的新一代云ERP,主要聚焦成长型、创新型企业,提供企业级云ERP整体解决方案。 0x02 漏洞概述 用友U8 Cloud存在多处(FileManageServlet和LoginVideoServlet)反序列化漏洞,系统未将…...

acwing算法基础之数据结构--STL简介
目录 1 基础知识2 模板3 使用示例3.1 vector3.2 pair3.3 string3.4 queue 1 基础知识 无。 2 模板 vector, 变长数组,倍增的思想size() 返回元素个数empty() 返回是否为空clear() 清空front()/back() 使用时,必须判断向量类容器非空push_back()/po…...
【Python深入学习】- 书籍推荐|数据结构和算法介绍|内建集合数据类型
🌈个人主页: Aileen_0v0 🔥系列专栏:PYTHON学习系列专栏 💫"没有罗马,那就自己创造罗马~" 若把编写代码比作行军打仗,那么要想称霸沙场,不能仅靠手中的利刃,还需深谙兵法。Python是一把利刃&…...

物联网对接协议
物联网对接协议有很多种,以下是几种常见的物联网对接协议: Modbus:是一种强大的通信标准,广泛应用于工业自动化和SCADA系统,以便将仪表、传感器和执行器的信号发送回主控制器。 Modbus具有广泛的通信协议,…...
腾讯待办关停,导出的数据怎么恢复到手机上面?
相信有不少腾讯待办的用户都发现了其“业务关停通知”,确实如此,由于业务调整,腾讯待办将于2023年的12月20日全面停止运营并下架,这就表示以后我们无法继续使用它了。在腾讯待办关停之前,绝大多数用户需要做的就是及时…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
