基于指数分布算法的无人机航迹规划-附代码
基于指数分布算法的无人机航迹规划
文章目录
- 基于指数分布算法的无人机航迹规划
- 1.指数分布搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用指数分布算法来优化无人机航迹规划。
1.指数分布搜索算法
指数分布算法原理请参考:https://blog.csdn.net/u011835903/article/details/131025569
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得指数分布搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用指数分布算法对航迹评价函数式(7)进行优化。优化结果如下:


从结果来看,指数分布算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于指数分布算法的无人机航迹规划-附代码
基于指数分布算法的无人机航迹规划 文章目录 基于指数分布算法的无人机航迹规划1.指数分布搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用指数分布算法来优化无人机航迹规划。 …...

vite基础学习笔记:13.Dialog 对话框 (用户注册与登录)
说明:自学做的笔记和记录,如有错误请指正 1. Dialog 对话框组件 目标效果:点击“登录/注册”,弹框 (1)创建全局组件,在官网中查询代码粘贴 (2) 注册和使用全局组件 &a…...

RedisTemplate 使用 pipeline 时需要注意的问题
RedisTemplate 使用 pipeline 时需要注意的问题 RedisTemplate 使用 pipeline 进行批量 set 时,需要把 key 和 value 都转为字节 1. 直接使用 getBytes() 转为字节,在读取数据时,会抛出以下序列化异常 //错误代码 protected void process(…...

uniapp 下载文件到手机
下载后端传递过来的文件 let thil this uni.showLoading({title: 下载中,mask:true }) uni.downloadFile({url: 接口地址, //仅为示例,并非真实的资源header: {"Authorization": token},responseType: blob,success: (res) > {if (res.statusCode 2…...

使用Drupal管理小型项目?试试Docker快速部署Drupal结合内网穿透实现远程访问
🎬 鸽芷咕:个人主页 🔥个人专栏:《Linux深造日志》《C干货基地》 ⛺️生活的理想,就是为了理想的生活! 文章目录 前言1. Docker安装Drupal2. 本地局域网访问3 . Linux 安装cpolar4. 配置Drupal公网访问地址5. 公网远程访问Drupal…...
BSP-STM32移植FreeRTOS
在stm32裸机工程中的Middlewares目录添加freeRtos源码 在裸机工程中的main中调用freertos接口...
【Spring】Spring IOCDI(万字详解)
文章目录 1. Spring是什么?2. 认识IOC2.1 传统程序开发1. Main.java2. Car.java3. Framework.java4. Bottom.java5. Tire.java 2.2 分析传统开发2.3 IOC程序开发1. Main.java2. Car.java3. Framework.java4. Bottom.java5. Tire.java 2.4 分析IOC开发2.5 IOC容器优点…...

ts 使用泛型来做类型映射
使用泛型来做类型映射,将对象(或数组)中类型转换为另一个类型 首先,定义一个类型Student // 定义一个类型Studentinterface Student {name: string,age: number}1、把Student的所有属性都变为可空的 type Nullable<T> {[p in keyof T]: T[p] || …...

Compose - 使用 Paging
一、添加依赖 查看官方最新版本 val paging_version "3.2.1" implementation("androidx.paging:paging-runtime:$paging_version") implementation("androidx.paging:paging-compose:$paging_version") 二、定义数据源 PagingSource 是对其它…...

数据结构与算法-(11)---有序表(OrderedList)
🌈个人主页: Aileen_0v0 🔥系列专栏:PYTHON学习系列专栏 💫"没有罗马,那就自己创造罗马~" 目录 知识回顾及总结 有序表的引入 编辑 实现有序表 1.有序表-类的构造方法 2.有序表-search方法的实现 3.有序表-add方法的实现…...

佳易王会员管理系统软件如何下载,基本功能有哪些
一、佳易王会员管理软件大众版 部分功能简介: 1、会员信息登记 :可以直接使用手机号登记,也可以使用实体卡片,推荐用手机号即可。 2、会员卡类型 :可以自由设置卡的类型,比如:充值卡、计次卡、…...

docker搭建mysql环境
1. 基础环境 名称描述CentOS 7.6Linux操作系统版本docker 20.10.5docker版本mysql 8.0.29mysql镜像版本 2. 下载安装 使用docker命令下载mysql镜像 [rootzhouwei ~]# docker pull mysql:8.0.29查看docker仓库是否已经下载了mysql镜像 [rootzhouwei ~]# docker images将mys…...

优思学院|推行精益六西格玛困难重重?7大原因分析助你避坑
六西格玛,是一种让企业在绩效管理的舞台上跳得更高更远的方法。它不仅仅是一套原则和技术,更是一种对完美的执着追求。 在这个舞台上,企业的流程管理得以严格、集中,质量得以高效提升。优思学院总结出六西格玛的核心是࿱…...

四川思维跳动商务信息咨询有限公司可信吗?
在今天的数字化时代,抖音带货已成为一种全新的商业模式。许多公司都在通过这种形式进行产品推广和销售,其中,四川思维跳动商务信息咨询有限公司以其专业的服务和良好的信誉,在抖音带货领域赢得了广泛赞誉。 四川思维跳动商务信息…...

高防CDN与高防服务器:谁更胜一筹?
在当今数字化世界中,网络安全对于保护网站和应用程序至关重要。在这一背景下,高防CDN和高防服务器是两种流行的解决方案,用于应对不同类型的网络攻击。本文将分析高防CDN是否能够替代高防服务器,以及它们各自的优势和限制。 高防C…...

2.Netty简单应用
引入Maven依赖 <dependency> <groupId>io.netty</groupId> <artifactId>netty-all</artifactId><version>4.1.49.Final</version> </dependency>服务端的管道处理器 public class NettyServerHandler extends ChannelInbou…...

80个10倍提升Excel技能的ChatGPT提示
你是否厌倦了在使用Excel时感觉像个新手?你是否想将你的技能提升到更高的水平,成为真正的Excel大师?嗯,如果你正在使用ChatGPT,那么成为Excel专家简直易如反掌。 你只需要了解一些最有用的Excel提示,就能在…...

jenkins结合k8s部署动态slave
1、完成k8s连接 在完成jenkins的部署后现安装kubernets的插件 如果jenkins 是部署在k8s集群中只需要填写一下 如果是非本集群的部署则需要填写证书等 cat ./config echo ‘certificate-authority-data-value’ | base64 -d > ./ca.crt echo ‘client-certificate-data’ |…...
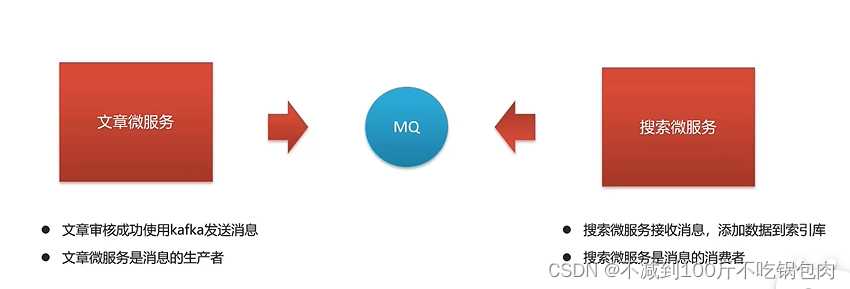
搜索引擎Elasticsearch基础与实践
倒排索引 将文档中的内容分词,然后形成词条。记录每条词条与数据的唯一表示如id的对应关系,形成的产物就是倒排索引,如下图: ElasticSearch数据的存储和搜索原理 这里的索引库相当于mysql中的database。一个文档(do…...

vue项目electron打包
1.设置国内镜像 npm config edit 命令行输入后会弹出npm的配置文档,需要文档末尾加入 electron_mirrorhttps://npm.taobao.org/mirrors/electron/ electron-builder-binaries_mirrorhttps://npm.taobao.org/mirrors/electron-builder-binaries/ 2.全局安装electron …...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
