数据结构——B树
文章目录
- B树
- 1. 概念
- 2. B树插入分析
- 3.插入过程
- 4. B树插入实现
- 5.B树验证
- 6. B树性能分析
- 7.B+树&B*树
- 8. 小结
- 9. B树的运用
- MyISAM
- InnoDB
- 10. 总结
B树
可以用于查询的数据结构非常的多,比如说二插搜索树、平衡树、哈希表、位图、布隆过滤器,但如果需要存储一些数据量极大的数据,上述的数据结构就很不适用了,内存是不一定放的下的,比如用平衡树搜索一个贼大的文件。
因为数据量非常大,一次性无法加载到内存中,那么就可以在平衡树中保存数据项需要查找的部分,以及指向该数据在磁盘中的地址的指针。
虽然在上诉方法在内存中存放的是数据的地址,真实的数据是在磁盘上,解决了内存占用的问题。但是也有一定的缺陷:
- 当数据量比较大的时候,比如使用的是红黑树,虽然时间复杂度是 O ( l o g n ) O(logn) O(logn),但数据量比较大的时候,树的高度是比较高的。
- 当数据量特别大时,树中的节点可能无法一次性加载到内存中,这就需要增加磁盘的I/O次数
解决办法:就是减少I/O的次数,降低树的高度,引入多叉平衡树(B树)
1. 概念
B树是一棵M阶(M>2)的B树,是一棵平衡的M路平衡搜索树,可以是空树或者满足一下性
质:
- 根节点至少有两个孩子
- 每个非根节点至少有 M / 2 − 1 M/2-1 M/2−1(上取整)个关键字,至多有 M − 1 M-1 M−1个关键字,并且以升序排列
例如:当M=3的时候,至少有3/2=1.5,向上取整等于2,2-1=1个关键字,最多是2个关键字 - 每个非根节点至少有 M / 2 M/2 M/2(上取整)个孩子,至多有M个孩子
例如:当M=3的时候,至少有3/2=1.5,向上取整等于2个孩子。最多有3个孩子。 - key[i]和key[i+1]之间的孩子节点的值介于key[i]、key[i+1]之间
- 所有的叶子节点都在同一层
2. B树插入分析
为了简单起见,假设M = 3. 即三叉树,每个节点中存储两个数据,两个数据可以将区间分割成三个部分,因此节点应该有三个孩子,为了后续实现简单期间,节点的结构如下:

注意:孩子永远比数据多一个。
插入过程当中,有可能需要分裂,分裂的
前提是:
假设,当前是要组成一个M路查找树,关键字数必须<=M-1**(这里关键字数**>M-1**就要进行节点拆分)**规则是:
把中间的元素,提取出来,放到父亲节点上,左边的单独构成一个节点,右边的单独构成一个节点。
假设用 53 , 139 , 75 , 49 , 145 , 36 , 101 {53,139,75,49,145,36,101} 53,139,75,49,145,36,101构造B树的过程如下:
- 先插入53和139

-
再插入75,插入75后按照插入排序的思想对元素进行排序

-
因为该节点的元素已经满了,就需要进行分裂
节点分裂的步骤:
- 找到节点数据域的中间位置
- 给一个新节点,将中间位置的数据移动到新创建的节点中
- 将中间位置的那个数据移动到父节点中
- 将节点的关系连接好

-
插入49和145
- 找到该元素的插入位置的位置
- 按照插入排序的思想将节点插入到该节点的合适位置
- 再检测是否满足B数的性质
- 满足插入结束,不满足对节点进行分裂

-
插入36
插入后违法了B树的性质,需要进行分裂

对cur节点进行分裂:
- 找到中间位置
- 将中间位置右侧元素移动到新节点中
- 将中间位置元素49移动到父节点parent中
- 将新节点的父节点修改成parent

-
插入数字101
- 在B树中找到该节点的插入位置
- 按照插入排序思想将该节点插入到指定位置
- 检测插入后的节点元素个数是否小于M
- 如果小于M插入完成,等于M则需要对该节点进行分裂


分裂完后,发现根节点也需要进行分裂,根节点分裂需要进行特殊处理,因为它会增加树的高度。

3.插入过程
-
如果树为空,直接插入新节点中,该节点为树的根节点
-
树非空,找待插入元素在树中的插入位置(注意:找到的插入节点位置一定在叶子节点中)
-
检测是否找到插入位置(假设树中的key唯一,即该元素已经存在时则不插入)
-
按照插入排序的思想将该元素插入到找到的节点中
-
检测该节点是否满足B-树的性质:即该节点中的元素个数是否等于M,如果小于则满足
-
如果插入后节点不满足B树的性质,需要对该节点进行分裂:
- 申请新节点
- 找到该节点的中间位置
- 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
- 将中间位置元素以及新节点往该节点的双亲节点中插入,即继续4
-
如果向上已经分裂到根节点的位置,插入结束
4. B树插入实现
B树的节点定义
// M叉树
private static final int M = 3;
static class BTreeNode {// 节点关键字int[] keys;// 孩子BTreeNode[] subs;// 关键字个数int keySize;// 父节点BTreeNode parent;public BTreeNode() {keys = new int[M];// 多给一个方便分裂subs = new BTreeNode[M+1];}
}定义一个类方便查找指定节点
public class Pair<K,V> {K key;V val;public Pair(K key, V val) {this.key = key;this.val = val;}
}
插入代码
/*** B树*/
public class BTree {// B树根节点BTreeNode root;public boolean insert(int key) {if (root == null) {root = new BTreeNode();root.keys[0] = key;root.keySize++;return true;}// 查找关键字是否已经存在Pair<BTreeNode,Integer> cur = find(key);if (cur.val != -1) {// 说明key已经存在,插入失败return false;}// 开始插入(插入排序)BTreeNode parent = cur.key;int i = 0;for (i = parent.keySize-1; i >= 0; i--) {if (parent.keys[i] >= key) {parent.keys[i+1] = parent.keys[i];} else {break;}}parent.keys[i+1] = key;parent.keySize++;// 判断是否需要分裂if (parent.keySize >= M) {split(parent);}return true;}/*** 对cur节点进行分裂* @param cur*/private void split(BTreeNode cur) {BTreeNode newNode = new BTreeNode();BTreeNode parent= cur.parent;// 中间位置int mid = cur.keySize>>1;// 把mid往后的元素移动到新节点int j = 0;int i = mid+1;for (; i < cur.keySize; i++) {newNode.keys[j] = cur.keys[i];// 子节点引用newNode.subs[j] = cur.subs[i];// 修改子节点的parent引用if (newNode.subs[j] != null) {newNode.subs[j].parent = newNode;}newNode.keySize++;j++;}// 多拷贝一次最后的子节点newNode.subs[j] = cur.subs[i];if (newNode.subs[j] != null) {newNode.subs[j].parent = newNode;}//更新分裂节点关键字个数,-1指的是mid位置的节点要向上提cur.keySize = cur.keySize-mid-1;// 处理根节点分裂情况!if (cur == root) {root = new BTreeNode();root.keys[0] = cur.keys[mid];root.keySize++;root.subs[0] = cur;root.subs[1] = newNode;cur.parent = root;newNode.parent = root;return;}// 更新新节点的父亲节点newNode.parent = parent;// 将mid位置的元素向上提int midVal = cur.keys[mid];i = parent.keySize-1;for (; i >= 0; i--) {if (parent.keys[i] >= midVal) {parent.keys[i+1] = parent.keys[i];parent.subs[i+2] = parent.subs[i+1];} else {break;}}parent.keys[i+1] = midVal;parent.keySize++;// 将当前父节点的孩子节点设置为newNodeparent.subs[i+2] = newNode;// 如果个数超过M递归分裂if (parent.keySize >= M) {split(parent);}}/*** 在B树中查找关键字是否已经存在* 找到返回节点和起下标,否则返回其父节点和-1* @param key* @return*/private Pair<BTreeNode, Integer> find(int key) {BTreeNode cur = root;BTreeNode parent = root;int index = 0;while (cur != null) {while (index < cur.keySize) {if (cur.keys[index] == key) {return new Pair<>(cur,index);} else if (cur.keys[index] < key) {index++;} else {break;}}parent = cur;// 向子节点找cur = cur.subs[index];index = 0;}return new Pair<>(parent,-1);}
}
5.B树验证
对B树进行中序遍历,只要打印出来的数据是有序说明插入正确
/*** 验证B树* @param root*/private void inorder(BTreeNode root){if(root == null)return;for(int i = 0; i < root.keySize; ++i){inorder(root.subs[i]);System.out.println(root.keys[i]);}inorder(root.subs[root.keySize]);}
6. B树性能分析
对于一棵节点为N度的B树,查找和插入需要 l o g M − 1 N log_{M-1}N logM−1N~ l o g M / 2 N log_{M/2}N logM/2N次比较。对于度为M的B树,每一个节点的子节点个数为 M / 2 M/2 M/2~ ( M − 1 ) (M-1) (M−1)之间,因此树的高度应该要在 l o g M − 1 N log_{M-1}N logM−1N和 l o g M / 2 N log_{M/2}N logM/2N之间,在定位到该节点后,再采用二分查找的方式可以很快的定位到该元素。
B树的效率是很高的对于 N = 62 ∗ 1000000000 N=62*1000000000 N=62∗1000000000个节点,如果M为1024,则 l o g M / 2 N < = 4 log_{M/2}N<=4 logM/2N<=4,既在620亿个元素中,如果这棵树的度为1024,则需要小于4次即可定位到该节点,然后利用二分查找,可以快速定位到该元素,大大减少了读取磁盘的次数。
总结:
- B树实际上是一棵M叉平衡树
- 非根节点的关键字数量[M/2-1,M-1],因为每次满了之后,会拷走一半
- 非根节点的孩子数量[M/2,M]
- 所有的叶子节点都在同一层,所以B树是天然平衡的
- M越大效率越高,但M越大也会有空间浪费的问题,节点分裂会拷走一半就会存在空间浪费的问题
7.B+树&B*树
B+树是B树的变形,也是一种多路搜索树:
其定义基本与B树相同,除了:
- B+树非叶子节点的子树指针与关键字个数相同,而B树的孩子数量比关键字多一个
- B+树非叶子节点的子树指针指向的子树都属于它的右子树,也就是大于当前节点
- 为所有叶子节点增加一个链指针,也就是叶子节点是一个链表
- B+数的叶子节点存储了数据,而非叶子节点只是存储了关键字。

对于B+树来说,如果要查找数据,那么一定得遍历整个树的高度,因为数据在叶子节点,但B树的每个节点都存储了数据,就不一定要遍历到叶子节点。
B+树的分裂:当一个结点满时,分配一个新的结点,
并将原结点中1/2的数据
复制到新结点,最后在父结点中增加新结点的指针,B+树的分裂只影响原结点和父
结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树
B*树是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

B树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了),如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
8. 小结
- B树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键
字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中; - B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引,B+树总是到叶子结点才命中;
- B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3;
9. B树的运用
B-树最常见的应用就是用来做索引。索引通俗的说就是为了方便用户快速找到所寻之物,比如:书籍目录可以让读
者快速找到相关信息,hao123网页导航网站,为了让用户能够快速的找到有价值的分类网站,本质上就是互联网
页面中的索引结构。
MySQL官方对索引的定义为:索引(index)是帮助MySQL高效获取数据的数据结构,简单来说:索引就是数据结
构。
注意:索引是基于表的,而不是基于数据库的。
MyISAM
MyISAM引擎是MySQL5.5.8版本之前默认的存储引擎,不支持事物,支持全文检索,使用B+Tree作为索引结构,
叶节点的data域存放的是数据记录的地址,其结构如下:

上图是以以Col1为主键,MyISAM的示意图,可以看出MyISAM的索引文件仅仅保存数据记录的地址**。在MyISAM中,主索引和辅助索引(Secondary key)在结构上没有任何区别,只是主索引要求key是唯一的,而辅助索引的key**可以重复。如果想在Col2上建立一个辅助索引,则此索引的结构如下图所示 :

同样也是一棵B+Tree,data域保存数据记录的地址。因此,MyISAM中索引检索的算法为首先按照B+Tree搜索算
法搜索索引,如果指定的Key存在,则取出其data域的值,然后以data域的值为地址,读取相应数据记录。
MyISAM的索引方式也叫做**“非聚集索引”**的
InnoDB
InnoDB存储引擎支持事务,其设计目标主要面向在线事务处理的应用,从MySQL数据库5.5.8版本开始,InnoDB存储引擎是默认的存储引擎。InnoDB支持B+树索引、全文索引、哈希索引。但InnoDB使用B+Tree作为索引结构
时,具体实现方式却与MyISAM截然不同。
第一个区别是InnoDB的数据文件本身就是索引文件。MyISAM索引文件和数据文件是分离的,索引文件仅保存数据记录的地址。而InnoDB索引,表数据文件本身就是按B+Tree组织的一个索引结构,这棵树的叶节点data域保
存了完整的数据记录。这个索引的key是数据表的主键,因此InnoDB表数据文件本身就是主索引。

上图是InnoDB主索引(同时也是数据文件)的示意图,可以看到叶节点包含了完整的数据记录,这种索引叫做聚集索引。因为InnoDB的数据文件本身要按主键聚集,所以InnoDB要求表必须有主键(MyISAM可以没有),如果没有显式指定,则MySQL系统会自动选择一个可以唯一标识数据记录的列作为主键,如果不存在这种列,则MySQL自动为InnoDB表生成一个隐含字段作为主键,这个字段长度为6个字节,类型为长整形。
第二个区别是InnoDB的辅助索引data域存储相应记录主键的值而不是地址,所有辅助索引都引用主键作为data
域。
**聚集索引这种实现方式使得按主键的搜索十分高效,但是辅助索引搜索需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录 **
10. 总结
-
像链表,顺序表这样的是否可以?
时间复杂度太高,不行
-
AVL树&红黑树是否可以?
数据量大时树的高度较高,增加了I/O次数 -
哈希表是否可以?
哈希表存在哈希冲突哈希只能支持 是或者不是。比如: where id =? 或者 where id =? 做不到范围查找: where id >10 -
为什么使用B+树,不适用B树?
- 节点点不存储data,这样一个节点就可以存储更多的key。可以使得树更矮,所以I/O操作次数更少。
- 叶子节点相连,更便于进行范围查找
聚簇索引和非聚簇索引的区别
- 聚簇索引将数据行存储在与索引相同的 B+ 树结构中,而非聚簇索引是将索引和主键 ID 存储在 B+ 树结构中;
- 数量限制不同:一张表只能有一个聚簇索引,但可以有多个非聚簇索引;
- 范围查询不同:聚簇索引中的数据行与索引行是一一对应的,因此聚簇索引通常比非聚簇索引更适合范围查询,而非聚簇索引需要进行两次查找:首先查找索引,然后查找数据行
- 非聚簇索引最大的缺点。 当查到索引对应的指针或主键后,可能还需要根据指针或主键再到数据文件或表中查询,首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录
- 在Innodb下主键索引是聚集索引,在Myisam下主键索引是非聚集索引
- MyISAM 不提供事务支持。InnoDB 提供事务支持,实现了 SQL 标准定义了四个隔离级别。
- MyISAM 不支持外键,而 InnoDB 支持。
相关文章:

数据结构——B树
文章目录 B树1. 概念2. B树插入分析3.插入过程4. B树插入实现5.B树验证6. B树性能分析7.B树&B*树8. 小结9. B树的运用MyISAMInnoDB 10. 总结 B树 可以用于查询的数据结构非常的多,比如说二插搜索树、平衡树、哈希表、位图、布隆过滤器,但如果需要存…...

java--String
1.String创建对象封装字符串数据的方式 ①方式一:java程序中的所有字符串文字(例如"abc")都为此类的对象 ②方式二:调用String类的构造器初始化字符串对象。 2.String提供的操作字符串数据的常用方法...

ls命令区别
ls -lh:显示详细信息,其中其中文件大小是显示Kb或Mb。 ls -l:也会显示文件大小,只是显示的是字节。...

经典OJ题:随机链表的复制
目录 题目: 本题的解图关键在于画图与看图! 思路分析: 方法一:暴力求解法。 方法二:插入法 方法解析: 步骤一、插入 步骤二、 处理每一个copy的randdom指针⭐————重点 步骤三、拆卸节点 代码…...
HTML的初步学习
HTML HTML 描述网页的骨架, 标签化的语言. HTML 的执行是浏览器的工作,浏览器会解析 html 的内容,根据里面的代码,往页面上放东西,浏览器的工作归根结底,还是以汇编的形式在CPU上执行. 浏览器对于html语法格式的检查没有很严格,即使你写的代码有一些不合规范之处,浏览器也会尽可…...

小赢科技荣登“2023中国互联网成长型前二十家企业”,旗下小赢卡贷表现突出
近日,中国互联网协会和厦门市人民政府联合在厦门举办了中国互联网企业综合实力指数(2023)发布会暨百家企业论坛。在这次评选活动中,深圳小赢信息技术有限责任公司(以下简称:小赢科技)凭借其行业领先的技术创新、企业成长及社会责任等方面的卓越表现,被评选为“2023年中国互联网…...

@Cacheable 、 @CachePut 、@CacheEvict 注解
在 Application 类上添加注解 EnableCaching EnableCaching public class Application {public static void main(String[] args) {SpringApplication.run(Application.class, args);}}Cacheable 注解 能够让方法的返回值被缓存起来,后续的请求可以直接从缓存中获取结果。 示…...
【ChatGPT】人工智能的下一个前沿
🎊专栏【ChatGPT】 🌺每日一句:慢慢变好,我是,你也是 ⭐欢迎并且感谢大家指出我的问题 文章目录 一、引言 二、ChatGPT的工作原理 三、ChatGPT的主要特点 四、ChatGPT的应用场景 五、结论与展望 一、引言 随着人工智能技…...
chrome 一些详细信息查找的地方
可以获得chrome 信息的列表 缓存 #缓存位置# 浏览器事件...

小程序游戏对接广告收益微信小游戏抖音游戏软件
小程序游戏对接广告是一种常见的游戏开发模式,开发者可以通过在游戏中嵌入广告来获取收益。以下是一些与小程序游戏对接广告收益相关的关键信息: 小程序游戏广告平台选择: 选择适合你的小程序游戏的广告平台非常重要。不同的平台提供不同类型…...

将MSSQL字段类型由text改为ntext
-- 修改数据字段类型DECLARE DATATYPE nvarchar(128) SET DATATYPE (SELECT DATA_TYPE FROM INFORMATION_SCHEMA.COLUMNS WHERE TABLE_NAME your-table-name AND COLUMN_NAME your-column-name) IF DATATYPE text BEGIN-- 注意 text和ntext互转要先转为中间类型ALTER TABL…...

python怎么表示复数
Python是一种强大的编程语言,支持许多数据类型,其中包括复数。本文将介绍Python中如何表示复数。 一、什么是复数 复数是由实部和虚部组成的数,可以表示为abj,其中a是实部,b是虚部,j是虚数单位。 二、Py…...
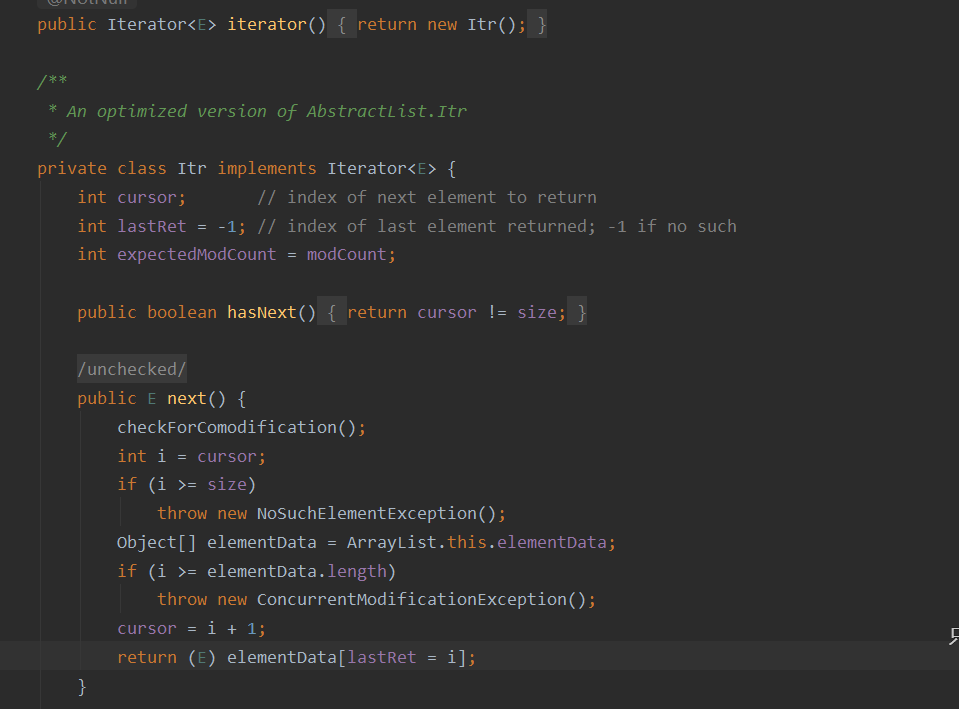
Java设计模式之迭代器模式
定义 提供一个对象来顺序访问聚合对象中的一系列数据,而不暴露聚合对象的内部表示。 结构 迭代器模式主要包含以下角色: 抽象聚合角色:定义存储、添加、删除聚合元素以及创建迭代器对象的接口。具体聚合角色:实现抽象聚合类&a…...

Qt 继承QAbstractListModel实现自定义ListModel
1.简介 QAbstractListModel是Qt框架中的一个抽象类,用于实现数据模型,用于在Qt的视图组件中展示和编辑列表数据。与QAbstractTableModel类似,它也是一个抽象类,提供了一些基本的接口和默认实现,可以方便地创建自定义的…...

TensorFlow2.0教程2-全连接神经网络以及深度学习技巧
文章目录 基础MLP网络1.回归任务2.分类任务mlp及深度学习常见技巧1.基础模型2.权重初始化3.激活函数4.优化器5.批正则化6.dropout基础MLP网络 1.回归任务 import tensorflow as tf import tensorflow.keras as keras import tensorflow.keras.layers as layers# 导入数据 (x_t…...

【OpenCV】Mat矩阵解析 Mat类赋值,单/双/三通道 Mat赋值
文章目录 1 Mat (int rows, int cols, int type)2 Mat 的其他矩阵3 Mat 的常用属性方法4 成员变量5 Mat赋值5.1 Mat(int rows, int cols, int type, const Scalar& s)5.2 数组赋值 或直接赋值5.2.1 3*3 单通道 img5.2.2 3*3 双通道 img5.2.3 3*3 三通道 imgOpenCV Mat类详解…...

微服务之Nacos注册管理
文章目录 一、Nacos安装步骤1.安装地址2.安装版本3.目录说明4.端口配置5.启动 二、Nacos服务注册1.Nacos依赖2.客户端修改配置文件3.启动效果图4.总结 三、Nacos服务集群属性1.服务跨集群调用问题2.服务集群属性3.总结 四、Nacos根据集群负载均衡1.修改配置文件2.设置集群服务类…...
Spring boot集成sentinel限流服务
Sentinel集成文档 Sentinel控制台 Sentinel本身不支持持久化,项目通过下载源码改造后,将规则配置持久化进nacos中,sentinel重启后,配置不会丢失。 架构图: 改造步骤: 接着我们就要改造Sentinel的源码。…...

软件测试|测试方法论—边界值
边界值分析法是一种很实用的黑盒测试用例方法,它具有很强的发现故障的能力。边界值分析法也是作为对等价类划分法的补充,测试用例来自等价类的边界。 这个方法其实是在测试实践当中发现,Bug 往往出现在定义域或值域的边界上,而不…...

OceanBase 笔记
目录 1. OceanBase 笔记1.1. 命令行 1. OceanBase 笔记 1.1. 命令行 # -usysoraclet#obcluster # -u用户名租户名#集群名...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
