刷题笔记day15-二叉树层序遍历
层序遍历
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/import ("container/list"
)func levelOrder(root *TreeNode) [][]int {// 思路1:此处肯定要使用队列result := [][]int{}if root == nil {return result}stack := list.New()stack.PushBack(root)for stack.Len() > 0 {stackLength := stack.Len()// 遍历每一层的所有节点newLis := []int{}for i := 0; i < stackLength; i++ {top := stack.Remove(stack.Front())node := top.(*TreeNode)newLis = append(newLis, node.Val)if node.Left != nil {stack.PushBack(node.Left)}if node.Right != nil {stack.PushBack(node.Right)}}result = append(result, newLis)}return result
}107. 二叉树的层序遍历 II
这个题的意思是从底到上进行层次遍历。我就直接将上一题的从上到下的遍历结果,做一次翻转既可。
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/func levelOrderBottom(root *TreeNode) [][]int {// 思路:相当于是之前从顶往下的结果,反转一下// 这次使用自定义的队列吧,就不使用 container/list 了var (result [][]int)if root == nil {return result}var que []*TreeNodeque = append(que, root)for len(que) > 0 {length := len(que)partResult := []int{}for i := 0; i < length; i++ {front := que[0]que = que[1:]partResult = append(partResult, front.Val)if front.Left != nil {que = append(que, front.Left)}if front.Right != nil {que = append(que, front.Right)}}result = append(result, partResult)}// 反转结果var newResult [][]intfor i := len(result) - 1; i >= 0; i-- {newResult = append(newResult, result[i])}return newResult
}199. 二叉树的右视图
目的:
思路:还是层次遍历,判断每一层 index 是否是最后一个。如果是,则将结果追加到result中。
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
import "container/list"func rightSideView(root *TreeNode) []int {// 我的思路是,层次遍历,每次访问一层的最右边的点。var result []intif root == nil {return result}que := list.New()que.PushBack(root)for que.Len() > 0 {length := que.Len()for i := 0; i < length; i++ {front := que.Remove(que.Front())node := front.(*TreeNode)// 每层最后一个放入result中。if i == length - 1 {result = append(result, node.Val)}if node.Left != nil {que.PushBack(node.Left)}if node.Right != nil {que.PushBack(node.Right)}}}return result
}
637. 二叉树的层平均值
还是层次遍历的思路,计算每一层的平均值。
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
import "container/list"func averageOfLevels(root *TreeNode) []float64 {// 思路:还是层次遍历,计算每一层的平均值。var result []float64if root == nil {return result}que := list.New()que.PushBack(root)for que.Len() > 0 {sum := 0length := que.Len()for i := 0; i < length; i++ {front := que.Remove(que.Front())node := front.(*TreeNode)sum += node.Valif node.Left != nil {que.PushBack(node.Left)}if node.Right != nil {que.PushBack(node.Right)}}result = append(result, float64(sum) / float64(length))}return result
}
429. N 叉树的层序遍历
换汤不换药
/*** Definition for a Node.* type Node struct {* Val int* Children []*Node* }*/import "container/list"func levelOrder(root *Node) [][]int {// 思路大差不差,依旧是层次遍历var result [][]intif root == nil {return result}que := list.New()que.PushBack(root)for que.Len() > 0 {length := que.Len()var partResult []intfor i := 0; i < length; i++ {front := que.Remove(que.Front())node := front.(*Node)partResult = append(partResult, node.Val)for _, item := range node.Children {que.PushBack(item)}}result = append(result, partResult)}return result
}
515.在每个树⾏中找最⼤值
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func largestValues(root *TreeNode) []int {var result []intif root == nil {return result}que := list.New()que.PushBack(root)for que.Len() > 0 {length := que.Len()maxValue := que.Front().Value.(*TreeNode).Valfor i := 0; i < length; i++ {front := que.Remove(que.Front())node := front.(*TreeNode)// 每层最后一个放入result中。if node.Val > maxValue {maxValue = node.Val}if node.Left != nil {que.PushBack(node.Left)}if node.Right != nil {que.PushBack(node.Right)}}result = append(result, maxValue)}return result
}
226.翻转二叉树
不可以使用 中序遍历,因为左边的调整完后,返回到根节点后,左边的换到右边,这是又开始调整“左边的”了,相当与右边的没动。
可是使用前序遍历、后序遍历。
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func invertTree(root *TreeNode) *TreeNode {// 思路:利用递归遍历,进行调整// 不可以使用 中序遍历,因为左边的调整完后,返回到根节点后,左边的换到右边,这是又开始调整“左边的”了,相当与右边的没动。// 三部曲:参数和返回值、单层逻辑、终止条件// 前序遍历:根左右if root == nil {return nil}root.Left, root.Right = root.Right, root.LeftinvertTree(root.Left)invertTree(root.Right)return root
}
相关文章:

刷题笔记day15-二叉树层序遍历
层序遍历 /*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/import ("container/list" )func levelOrder(root *TreeNode) [][]int {// 思路1:此处肯定要使用队列result : …...

前端 JS 经典:ES6 和 CommonJs 用法
1. 概念 都是 JavaScript 模块化规范,ES6 适用于浏览器端和 Node.js,CommonJs 适用于 Node.js。 2. 导出 // ES6 export function demo(n1, n2) {return n1 n2; }// CommonJS module.exports {demo: function (n1, n2) {return n1 n2;}, }; 3. 引入 …...

MacOS升级后命令行出现xcrun: error: invalid active developer path报错信息
在Mac上用g编译cpp文件时,出现以下(类似于工具环境问题的)报错: 解决方案:重新安装最新版的MacOS Command Line Tools xcode-select --install重新尝试编译: 编译成功(忽略这个warning&…...

【Qt】QPalette
2023年11月10日,周五上午 Palette意为“调色板”。 QPalette是Qt中用于管理控件调色板(颜色方案)的类。它允许你为Qt应用程序中的控件设置不同的颜色,以满足视觉设计需求。 QPalette可以管理各种控件的颜色属性,如前…...

专门为Web应用程序提供安全保护的设备-WAF
互联网网站面临着多种威胁,包括网络钓鱼和人为的恶意攻击等。这些威胁可能会导致数据泄露、系统崩溃等严重后果。 因此,我们需要采取更多有效的措施来保护网站的安全。其中WAF(Web application firewall,Web应用防火墙࿰…...

Android Camera App启动流程解析
前言:做了7年的camera app开发,给自己一个总结,算是对camera的一次告白吧。Camera被大家誉为手机的眼睛,是现在各大手机厂商的卖点,也是各大厂商重点发力的地方。Camera的重要性我就不在这里赘述了,让我们进…...

[工业自动化-8]:西门子S7-15xxx编程 - PLC主站 - CPU模块
目录 前言: 一、概述 二、CPU操作和显示 三、安装 四、CPU的选择 前言: 一、概述 西门子S7-1500系列是一系列高性能工业自动化控制器,广泛应用于制造业、自动化生产、物流等领域。这个系列的控制器是设计用来满足高性能、高效能要求的复…...
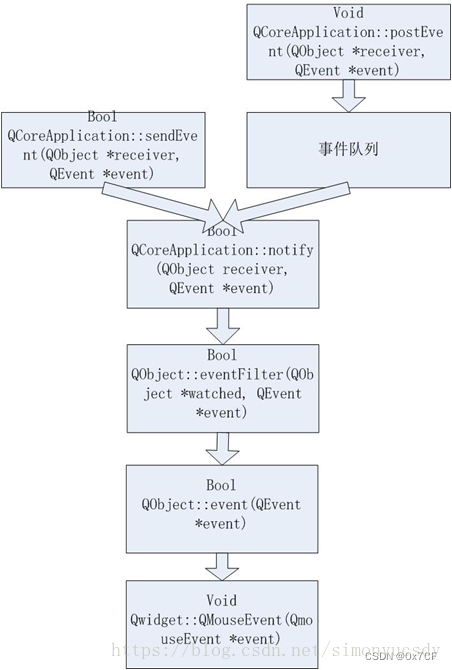
QT事件循环和事件队列的理解
Qt的事件循环机制_qt事件循环流程-CSDN博客 QT-事件循环机制_qt线程事件循环-CSDN博客 一、事件处理流程如图所示: 1.QCoreApplication::postEvent(QObject *receiver,QEvent *event): QCoreApplication::postEvent()函数用于将事件异步地发送到目标对…...

【Android】画面卡顿优化列表流畅度一
卡顿渲染耗时如图: 卡顿表现有如下几个方面: 网络图片渲染耗时大上下滑动反应慢,甚至画面不动新增一页数据加载渲染时耗时比较大,上下滑动几乎没有反应,画面停止没有交互响应 背景 实际上这套数据加载逻辑已经运行…...

SNP应邀参加2023中国企业数字化转型峰会暨赛意用户大会
创新驱动科技,数智驱动未来。如今,我国产业数字化进程提速升级,数字产业化规模持续壮大。数据显示,2022年,我国数字经济规模达50.2万亿元,总量稳居世界第二。数字经济已经成为推动传统产业转型升级、促进高…...
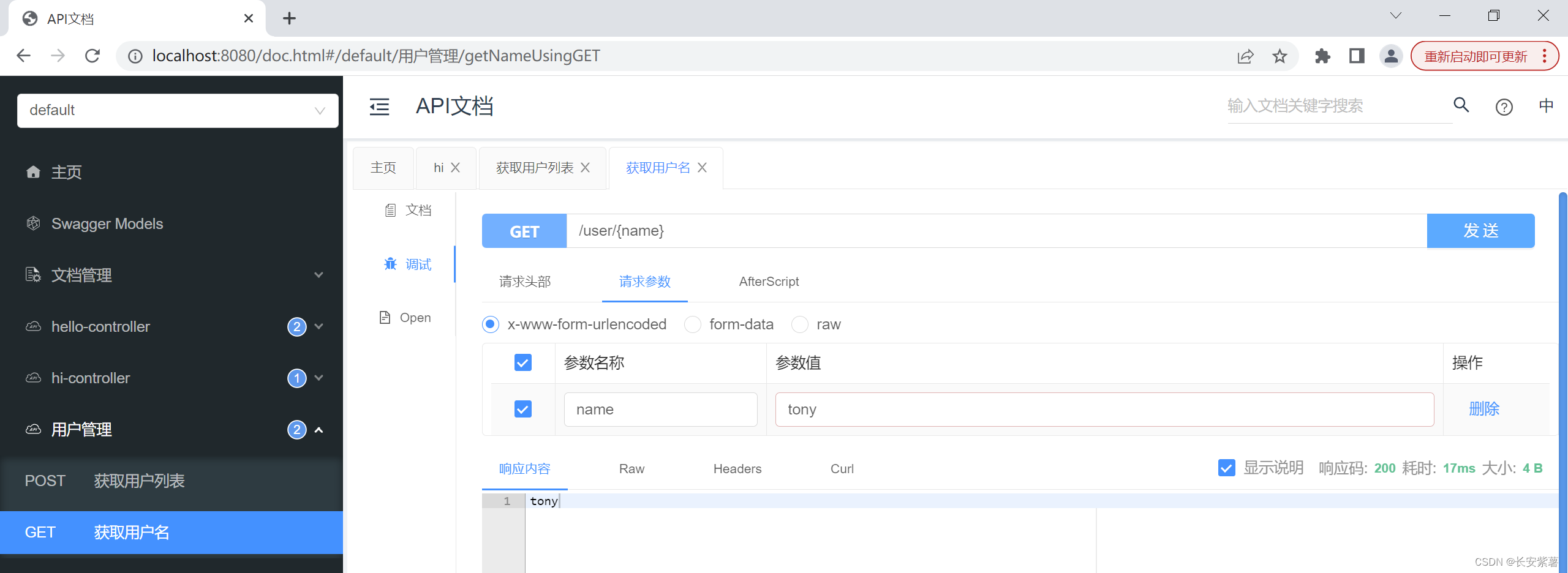
黑豹程序员-架构师学习路线图-百科:Knife4j API接口文档管理
文章目录 由来:接口文档第一代:Swagger第二代:Knife4j界面 由来:接口文档 古老编程是一个语言前后端通吃,ASP、JSP、PHP都是如此。 但随着项目规模变大,项目团队也开始壮大,岗位职责开始细分&a…...

PHP安全问题:远程溢出、DoS、safe_mode绕过漏洞
一、Web 服务器安全 PHP 其实不过是 Web服务器的一个模块功能,所以首先要保证 Web服务器的安全。当 然 Web服务器要安全又必须是先保证系统安全,这样就扯远了, 无穷无尽。PHP可以和各种 Web 服务器结合,这里也只讨论 Apache。非常建议以 chroot 方式安装启动 Apache,这样…...

2023云计算发展
未来的云计算世界将是一个充满着无限可能和创意的世界。在这个世界中,人们可以通过云计算技术实现更加便捷、安全、高效的日常生活,同时可以探索更加广阔、神奇的世界。 智能家居将成为云计算的新宠。未来,人们可以通过语音、手势、传感器等…...
泛型,异常)
javaSE学习笔记(六)泛型,异常
五、泛型 泛型的由来:通过Object转型问题引入--为了解决安全隐患 早期的Object类型可以接收任意的对象类型,但是在实际的使用中,会有类型转换异常的问题 泛型作用 提高安全性(将运行期的错误转换到编译期) 省去强转的麻烦,取…...
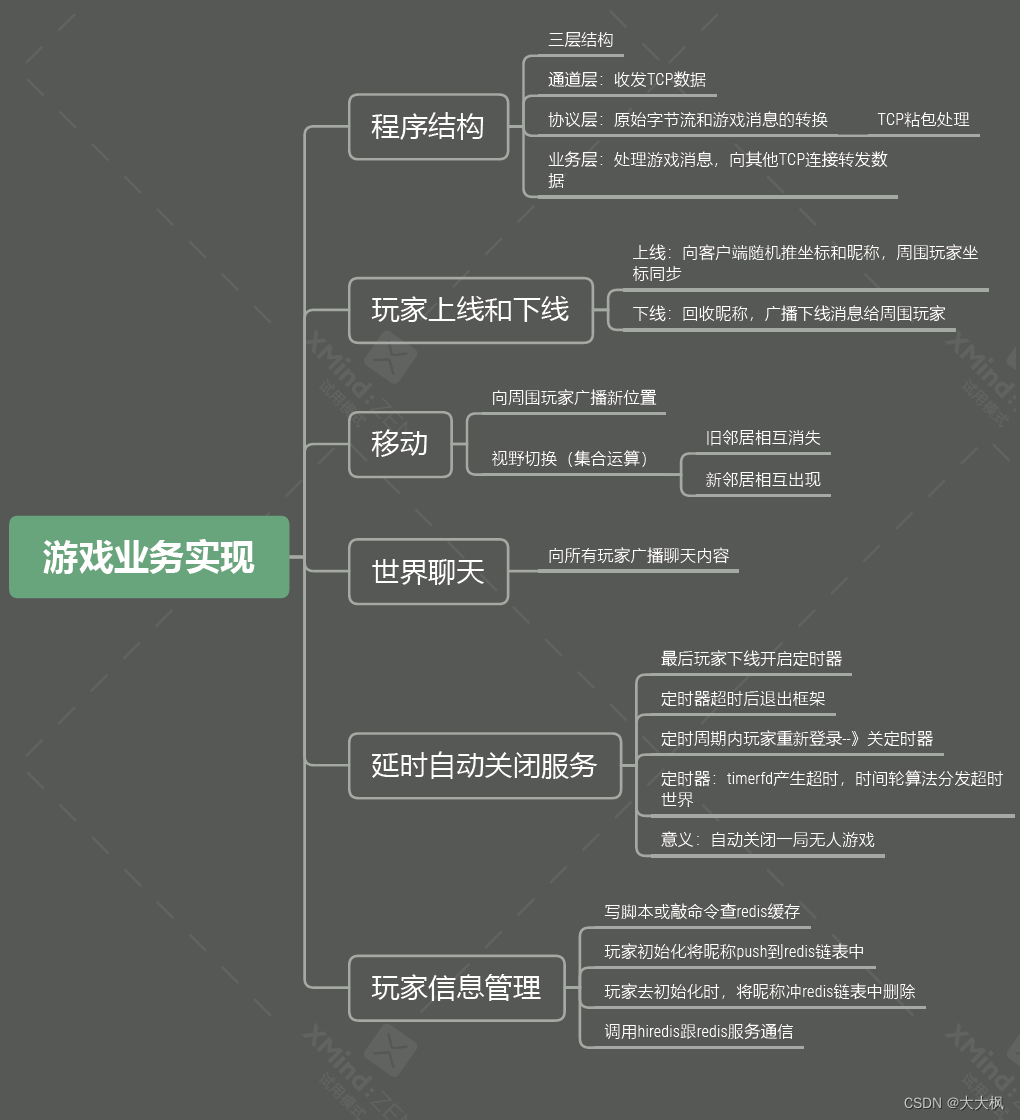
C/C++轻量级并发TCP服务器框架Zinx-游戏服务器开发006:基于redis查找玩家姓名+游戏业务实现总结
文章目录 1 Redis的安装与API的使用1.1 安装目录及环境变量1.2 设置远程客户端连接和守护进程1.3 启动redis1.4 Hiredis API的使用1.5 我的动态库和头文件 2 Redis的使用2.1 初始化时候2.2 结束的时候 3 测试4 Makefile5 游戏业务总结 1 Redis的安装与API的使用 1.1 安装目录及…...

数字政府!3DCAT实时云渲染助推上海湾区数字孪生平台
数字孪生,是一种利用物理模型、传感器数据、运行历史等信息,在虚拟空间中构建实体对象或系统的精确映射,从而实现对其全生命周期的仿真、优化和管理的技术。数字孪生可以应用于各个领域,如工业制造、智慧城市、医疗健康、教育培训…...

react之Component存在的2个问题
问题 只要执行setState(),即使不改变状态数据,组件也会重新render()只当前组件重新render(),就会自动重新render子组件 原因 Component中的shouldComponentUpdate()总是返回true 思路 只有当组件的state或props数据发生改变时才重新rend…...
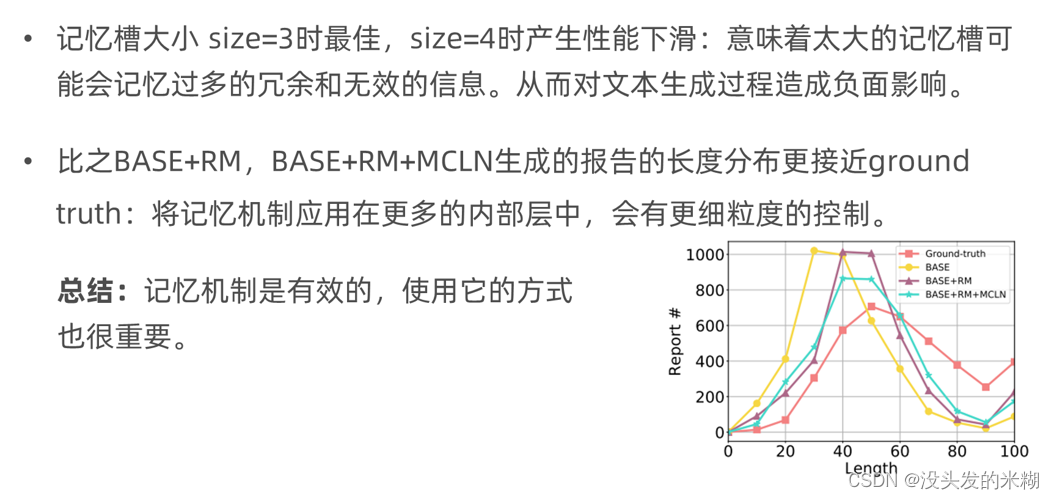
【论文阅读】Generating Radiology Reports via Memory-driven Transformer (EMNLP 2020)
资料链接 论文原文:https://arxiv.org/pdf/2010.16056v2.pdf 代码链接(含数据集):https://github.com/cuhksz-nlp/R2Gen/ 背景与动机 这篇文章的标题是“Generating Radiology Reports via Memory-driven Transformer”…...
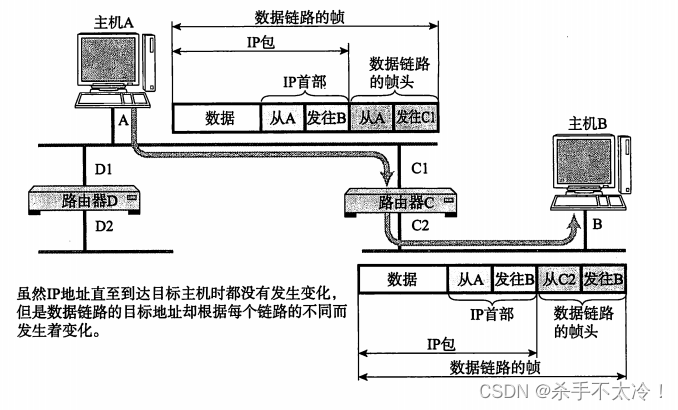
IP协议相关技术
文章目录 IP协议相关技术仅凭IP无法完成通信DNSARP IP协议相关技术 仅凭IP无法完成通信 人们在上网的时候其实很少直接输入某个具体的IP地址。 在访问Web站点和发送、接收电子邮件时,我们通常会直接输入Web网站的地址或电子邮件地址等那些由应用层提供的地址&…...
Visual Studio2022安装教程【图文详解】(大一小白)编译软件
工欲善其事,必先利其器。想要学好编程,首先要把手中的工具利用好,今天小编教一下大家如何下载安装并使用史上最强大的编译器--Visual Studio🍗 一.Visual Studio下载及安装 https://visualstudio.microsoft.com/ 打开文件 点击.ex…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
