XOR Construction

思路:
通过题目可以得出结论
b1^b2=a1
b2^b3=a2
.......
bn-1^bn=an-1
所以就可以得出
(b1^b2)^(b2^b3)=a1^a2
b1^b3=a1^a2
有因为当确定一个数的时候就可以通过异或得到其他所有的数,且题目所求的是一个n-1的全排列
那么求出a的前缀异或和arr之后就得到bi=b1^arri
实际上实在寻找一个 b1 使得异或出来的所有值越小越好,所以拆位,假设所有数字的第 i位为 1 的个数大于为 0 的个数,那我们最好异或上一个 2^i,这样可以使大部分数字变小。
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
#include<unordered_map>
#include<map>
#include<bitset>
#include<cstring>
#include <unordered_set>
//#include<priority_queue>
#include<queue>
#include<deque>
#include<set>
#include<stdlib.h>
#define dbug cout<<"*****hear*****"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"//交互题一定要关!!!!!!!!!
#define lowbit(x) (x&-x)
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;ll INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// int get_len(int x1,int y1,int x2,int y2)
// {
// return (x2-x1)*(x2-x1) + (y2-y1)*(y2-y1);
// }
const ll N = 2e5+ 10;const ll mod1 =998244353;const ll mod2 =1e9+7;
// const ll hash_num = 3e9+9;
ll n,m,ca;
ll arr[N],brr[N],crr[N],drr[N];
//ll h[N],ne[N],e[N],w[N],book[N],idx;
//ll idx;// void add(ll a, ll b , ll c)
// {
// e[idx] = b, w[idx] = c,ne[idx] = h[a], h[a] =idx ++ ;
// }void solve()
{cin >> n;arr[0]=0;rep(i,1,n-1){cin >> arr[i];arr[i] ^= arr[i-1];}ll ans=0;rep(i,0,20){ll sum1=0;ll sum2=0;rep(j,0,n-1){if(arr[j]>>i&1)sum1++;else{sum2++;}}if(sum1>sum2)ans|=1<<i;}rep(i,0,n-1)arr[i]^=ans;rep(i,0,n-1)cout << arr[i]<<' ';
}int main()
{IOS;ll _;_=1;//scanf("%lld",&_);//cin>>_;ca=1;while(_--){solve(); ca++;} return 0;
}
相关文章:

XOR Construction
思路: 通过题目可以得出结论 b1^b2a1 b2^b3a2 ....... bn-1^bnan-1 所以就可以得出 (b1^b2)^(b2^b3)a1^a2 b1^b3a1^a2 有因为当确定一个数的时候就可以通过异或得到其他所有的数,且题目所求的是一个n-1的全排列 那么求出a的前缀异或和arr之后…...
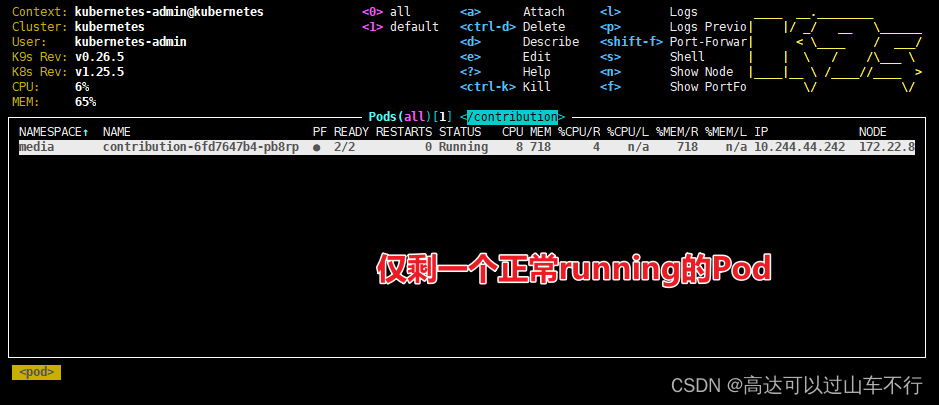
K8S容器持续Terminating无法正常关闭(sider-car容器异常,微服务容器正常)
问题 K8S上出现大量持续terminating的Pod,无法通过常规命令删除。需要编写脚本批量强制删除持续temminating的Pod:contribution-xxxxxxx。 解决 获取terminating状态的pod名称的命令: # 获取media命名空间下,名称带contributi…...

Spring 循环依赖
文章目录 内容总结循环依赖 内容总结 循环依赖 循环依赖只存在于 Spring 中, 是因为 Spring 创建 Bean 的流程中, 依赖注入阶段, 会先从单例池中找, 没有再从定义池中找, 针对定义池中找到的候选项会通过 getBean 创建其单例并缓存到单例池, 此机制导致了存在循环依赖的问题.…...

MySQL 8.0.13升级到8.0.35记录 .NET
1、修改表结构的字符集 utf8 修改成 utf8mb4 utf8_general_ci 修改成 utf8mb4_0900_ai_ci 注:所有地方都要替换。 否则会报错误提示:Character set utf8mb3 is not supported 下面是.NET环境升级遇到的问题 2、MySQL Connector Net 8.0.13 在程…...

flink udtaf 常年不能用
[FLINK-32807] when i use emitUpdateWithRetract of udtagg,bug error - ASF JIRA flink1.18发布的时候 他都显示未解决 但是文档上一直有udtaf...

路由汇总的四要点
1.是基于链路级的还是进程级的? RIP和eigrp都是基于接口的链路级汇总,而OSPF是基于进程的 2.汇总路由什么时候消失? 最后一条明细路由消失的时候,汇总路由消失。 3.汇总之后,汇总路由被通告,本地是否会产生一条指向NULL接口的…...
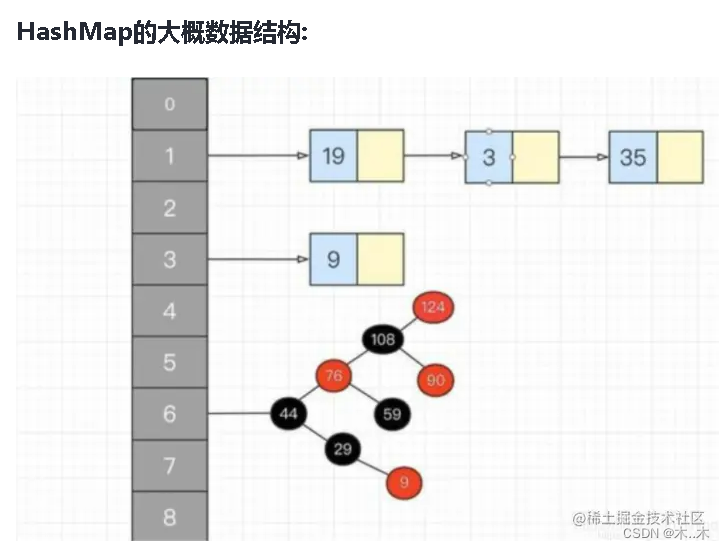
HashMap存值、取值及哈希碰撞原理分析
HashMap中的put()和get()的实现原理: map.put(k,v)实现原理 首先将k,v封装到Node对象当中(节点)。 然后它的底层会调用K的hashCode()方法得出hash值。 通过哈希表函数/哈希算法,将hash值转换成数组的下标,下标位置上…...

【SVN】
SVN 1 svn使用1.1 主干合并到分支1.2 分支合并到主干1.3 分支建立1.4 创建分支1.5 切换分支1.6 合并分支1.7 删除分支 2 概念理解 1 svn使用 1.1 主干合并到分支 首先,在本地trunk中先update一下,有冲突的解决冲突,保证trunk和repository已…...

编程语言,脚本语言
脚本语言上手快,快速实现一个小应用如python;编程语言重型,需复杂的设计和较长时间的开发,如java、c...
探索双十一:从技术角度剖析电商狂欢节
每年的11月11日,全球最大的在线购物狂欢节“双十一”在中国掀起了一场规模空前的消费风暴。以阿里巴巴为代表的电商平台和众多品牌商家,不仅为消费者提供了数以亿计的优惠商品,同时也将这一活动打造成了一个科技与商业完美结合的标志事件。本…...
Ubuntu LTS 坚持 10 年更新不动摇
Linux 内核开发者 Jonathan Corbet 此前在欧洲开源峰会上宣布,LTS 内核的支持时间将从六年缩短至两年,原因在于缺乏使用和缺乏支持。稳定版内核维护者 Greg Kroah-Hartman 也表示 “没人用 LTS 内核”。 近日,Ubuntu 开发商 Canonical 发表博…...

Python将多个相同格式的变量存储到列表中
在日常写代码过程中往往会遇到多个相同格式名称的变量需要存储到一个list。 怎么优雅地写出来呢 首先定义变量,然后使用列表推导式存储到列表中 # 定义变量 a_1, a_2 , # 列表推导式完成 a_list [globals()[fa_{i}] for i in range(1, 3)]...

前端字符串转数组对象实现方式-开发bug总结6
问题描述: 后台管理系统,这次投产完线上出现了个问题!element-ui组件下拉选项框打开全部都是无数据,而且控制台报错,但是新添加的数据是正常显示的。对比了原因之后发现,新的数据前端传给后端的格式&#…...
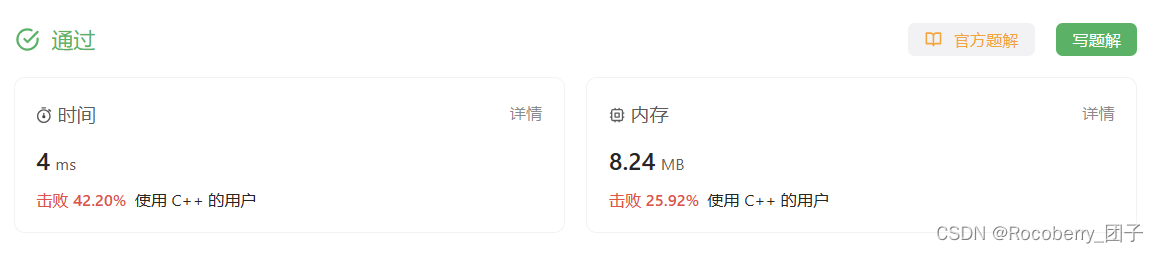
99 颜色分类
颜色分类 题解1 双指针题解2 单指针 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在…...

计算机视觉与深度学习 | 基于GPS/BDS多星座加权图因子优化的行人智能手机导航
===================================================== github:https://github.com/MichaelBeechan CSDN:https://blog.csdn.net/u011344545 ===================================================== 基于GPS/BDS多星座加权图因子优化的行人智能手机导航 1、引言2、相关工…...
低代码平台,业务开发的“银弹”
目录 一、为什么需要低代码平台 二、低代码平台的搭建能力 三、低代码其他能力 四、写在最后 随着互联网和信息技术的快速发展,各行各业都在积极拥抱数字化转型。在这个过程中,软件开发成为企业实现数字化转型的关键环节。然而,传统的软件开发…...
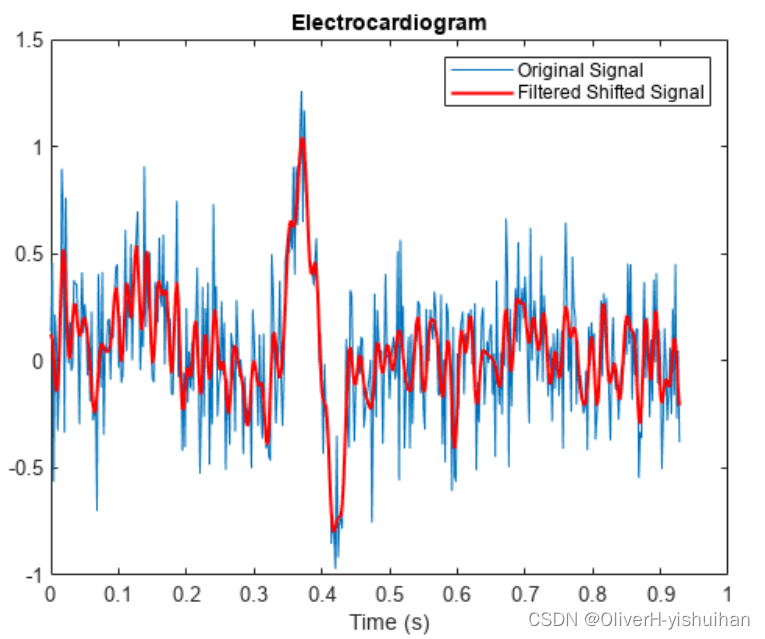
补偿 FIR 滤波器引入的延迟
补偿 FIR 滤波器引入的延迟 对信号进行滤波会引入延迟。这意味着相对于输入,输出信号在时间上有所偏移。此示例向您说明如何抵消这种影响。 有限冲激响应滤波器经常将所有频率分量延迟相同的时间量。这样,我们就很容易通过对信号进行时移处理来针对延迟…...
图数据库Neo4j详解
文章目录 第一章 图和Neo4j1.1 图数据库概念1.1.1 图论起源1.1.2 节点-关系及图1.1.3 图数据库1.1.4 图数据库分类1.1.4 图数据库应用场景1.1.5 与关系型数据库对比1.1.6 图数据库优势 1.2 Neo4j介绍1.2.1 Neo4j是什么1.2.2 Neo4j特点1.2.3 Neo4j的优势1.2.4 Neo4j的限制1.2.5 …...

系列一、Shiro概述
一、概述 Shiro是一款主流的Java安全框架,不依赖任何容器,可以运行在JavaSE 和 JavaEE项目中,它的主要作用是对访问系统的用户进行身份认证、授权、会话管理、加密等操作。 一句话:Shiro是一个用来解决安全管理的系统框架&#x…...

SpringCloudAlibaba——Sentinel
Sentinel也就是我们之前的Hystrix,而且比Hystrix功能更加的强大。Sentinel是分布式系统的流量防卫兵,以流量为切入点,从流量控制、流量路由、熔断降级等多个维度保护服务的稳定性。 Sentinel采用的是懒加载,这个接口被访问一次&a…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
