【数据结构】树的基本性质(计算树的总结点数与叶结点数)
树的基本性质
- ⭐️计算树的总结点与叶结点数
- 💫性质1
- 💫性质2
- 💫例题1
- 💫例题2
⭐️计算树的总结点与叶结点数
💫性质1
性质1 树中的结点数等于所有结点的度数之和加1
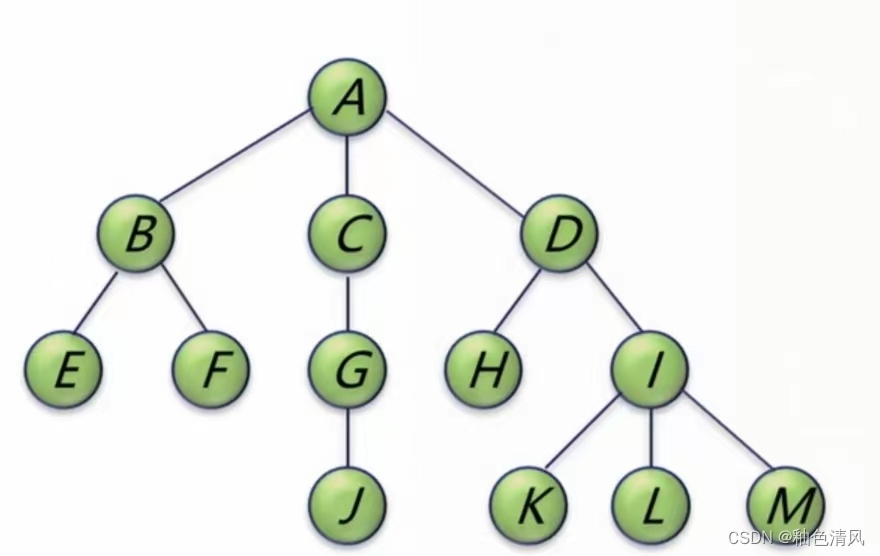
例如上面这棵树,A的孩子为B、C、D,A的度数为3;B的孩子为E、F,B的度数为2;C的孩子为G,C的度数为1;D的孩子为H、I,D的度数为2…
结点数=A的度数+B的度数+C的度数+D的度数+…+J的度数+K的度数+L的度数+M的度数+1
=(B+C+D)+(E+F)+G+(H+I)+…+0+0+0+0+1
也就是结点数等于每个结点的孩子树之和(度之和)再加1,这个1就是根节点。
总结点数:n=13;
树的度:m=3;
n0(度为0的结点数)=7;
n1(度为1的结点数)=2;
n2(度为2的结点数) =2;
n3(度为3的结点数)=2;
n = 7 ∗ 0 + 2 ∗ 1 + 2 ∗ 2 + 2 ∗ 3 + 1 n=7*0+2*1+2*2+2*3+1 n=7∗0+2∗1+2∗2+2∗3+1
💫性质2
性质2 结点表示个数:n为总结点个数, n i {n_i} ni为度为i(0≤i≤m)的结点个数,则 n = n 0 + n 1 + . . . + n m {n=n_0+n_1+...+n_m} n=n0+n1+...+nm

对于上面这棵树
总结点树 n=13;
这树的度数m=3;
n 0 {n_0} n0=7;
n 1 {n_1} n1=2;
n 2 {n_2} n2=2;
n 3 {n_3} n3=2;
n = n 0 + n 1 + n 2 + n 3 n={n_0+n_1+n_2+n_3} n=n0+n1+n2+n3
对于上面两种计算树的结点的方法,我认为一个是从一个结点本身出发,计算它自己本身;另一种是从它的孩子出发,计算之和 ,但由于这样树的根节点没有被纪录,所以不要忘了加1。
💫例题1
一颗树度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数为()
A.41 B.82 C.113 D.122
分析:
从两种角度出发:
从结点自身:
总结点 n = 20 + 10 + 1 + 10 + n 0 n=20+10+1+10+n_0 n=20+10+1+10+n0
从结点的孩子:
总结点 n = 20 ∗ 4 + 10 ∗ 3 + 1 ∗ 2 + 10 ∗ 1 + 1 n=20*4+10*3+1*2+10*1+1 n=20∗4+10∗3+1∗2+10∗1+1
联立上面两式,可以解得 n 0 = 82 n_0=82 n0=82
💫例题2
已知一棵树度为m的树中有 n 1 n_1 n1个度为1的结点, n 2 n_2 n2个度为2的结点,…, n m n_m nm个度为m的结点,问该树中有多少个叶子结点?
设总结点n
则 n = n 1 + n 2 + . . . + n m + n 0 n=n_1+n_2+...+n_m+n_0 n=n1+n2+...+nm+n0
且 n = 1 ∗ n 1 + 2 ∗ n 2 + 3 ∗ n 3 + . . . + m ∗ n m + 1 n=1*n_1+2*n_2+3*n3+...+m*n_m+1 n=1∗n1+2∗n2+3∗n3+...+m∗nm+1
联立解得, n 0 = n 2 + 2 n 3 + 3 n 4 + . . . + ( m − 1 ) n m + 1 n_0=n_2+2n_3+3n_4+...+(m-1)n_m+1 n0=n2+2n3+3n4+...+(m−1)nm+1
相关文章:

【数据结构】树的基本性质(计算树的总结点数与叶结点数)
树的基本性质 ⭐️计算树的总结点与叶结点数💫性质1💫性质2💫例题1💫例题2 ⭐️计算树的总结点与叶结点数 💫性质1 性质1 树中的结点数等于所有结点的度数之和加1 例如上面这棵树,A的孩子为B、C、D&…...
android手机平板拓展电脑屏幕
有这么两个软件 spacedesk_driver_Win_10_64_v1065_BETA.msi 安装在电脑上 spacedeskv0.91.1_chinese.apk 安装在android设备上 同一个局域网投屏就好了。 局域网无限投屏是很吃带宽的。 建议usb共享网络,不占用带宽、延迟低。 下载地址: https:/…...

接口测试的流程
接口通俗的理解就是不同部分之间的连接通道,可以是程序之内的,也可以是不同程序之间的。一般公司都会要求做接口测试,因为这是测试前移和测试左移的一种方式,会极大的解决bug的成本。 接口测试流程 接口测试的流程一般包括&…...

HMAC 详解:在 Golang 中实现消息认证码
目录 什么是 HMAC HMAC 的主要用途 HMAC 的工作原理 Golang 中的 crypto/hmac 包 如何选择合适的哈希函数和密钥长度 小结 什么是 HMAC HMAC(Hash-based Message Authentication Code)是一种基于 Hash 函数和密钥的消息认证码,由 H.Kr…...
阻塞队列和定时器的使用
阻塞队列 谈到队列,大家就能想到队列的先进先出原则,但有些特殊的队列,虽然也是先进先出的,但是带有阻塞功能,我们把这种队列叫做阻塞队列. ★如果队列为空,执行出队操作就会阻塞,阻塞到另外一个线程往队列里添加元素(队列不为空)为止. ★如果队列满了,执行入队操作时,也会阻…...
JavaScript脚本操作CSS
脚本化CSS就是使用JavaScript脚本操作CSS,配合HTML5、Ajax、jQuery等技术,可以设计出细腻、逼真的页面特效和交互行为,提升用户体验,如网页对象的显示/隐藏、定位、变形、运动等动态样式。 1、CSS脚本化基础 CSS样式有两种形式&…...

Rust4.1 Managing Growing Projects with Packages, Crates, and Modules
Rust学习笔记 Rust编程语言入门教程课程笔记 参考教材: The Rust Programming Language (by Steve Klabnik and Carol Nichols, with contributions from the Rust Community) Lecture 7: Managing Growing Projects with Packages, Crates, and Modules src/main.rs // s…...

RPA在财务预测和分析中的应用
在现代企业管理中,财务数据分析是决策制定和战略规划的关键环节。大数据的兴起带来财务数据的复杂性和数量不断增加,企业为此消耗了大量人力和物力。随着当今数字化、智能化时代的到来,越来越多企业引进RPA技术来提高工作效率,实现…...

无人机航拍技术基础入门,无人机拍摄的方法与技巧
一、教程描述 买了无人机,可是我不敢飞怎么办?禁飞区越来越多,到底哪儿才能飞?我的无人机跟你一样,为什么我拍不出大片?厂家的说明书看不进去,有没有一套无人机的课程,可以快速上手…...
)
PTA 哈密尔回路(建图搜索)
题目 著名的“汉密尔顿(Hamilton)回路问题”是要找一个能遍历图中所有顶点的简单回路(即每个顶点只访问 1 次)。本题就要求你判断任一给定的回路是否汉密尔顿回路。 输入格式: 首先第一行给出两个正整数:…...

如何利用产品帮助中心提升用户体验
在当今竞争激烈的市场中,提供优秀的用户体验是吸引和保留客户的关键。而一个高效和易于使用的产品帮助中心,正成为越来越多企业用以提升用户体验的重要工具。产品帮助中心是一个集中的信息库,为用户提供关于产品功能、故障排除、常见问题解答…...
【Python大数据笔记_day05_Hive基础操作】
一.SQL,Hive和MapReduce的关系 用户在hive上编写sql语句,hive把sql语句转化为MapReduce程序去执行 二.Hive架构映射流程 用户接口: 包括CLI、JDBC/ODBC、WebGUI,CLI(command line interface)为shell命令行;Hive中的Thrift服务器允许外部客户端…...

css呼吸效果实现
实现一个图片有规律的大小变化,呈现呼吸效果,怎么用CSS实现这个呼吸效果呢 一.实现 CSS实现动态效果可以使用动画( animation)来属性实现,放大缩小效果可以用transform: scale来实现,在这基础上有了动画,就可以设置一个…...

机器视觉opencv答题卡识别系统 计算机竞赛
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 答题卡识别系统 - opencv python 图像识别 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🥇学长这里给一个题目综合评分(每项满分5分…...

2024年的后端和Web开发趋势
目录 1 2 3 4 5 1 不断变化的数字创新格局可能让人感觉像是一场无情的竞赛。作为开发人员,你的痛苦是真实的——交付尖端产品、保持竞争力、跟上不断变化的用户期望,综合起来你的压力可能是压倒性的。 但是,如果我们告诉你有一个指南针…...
对比了10+网盘资源搜索工具,我最终选择了这款爆赞的阿里云盘、百度网盘、夸克网盘资源一站式搜索工具
盘友圈(https://panyq.com)是一个综合性的网盘搜索站,与其他网盘搜索工具相比,它具有多个独特的优点,使其成为用户们首选的平台。 首先,盘友圈汇集了阿里云盘、百度网盘和夸克网盘等主流网盘资源ÿ…...
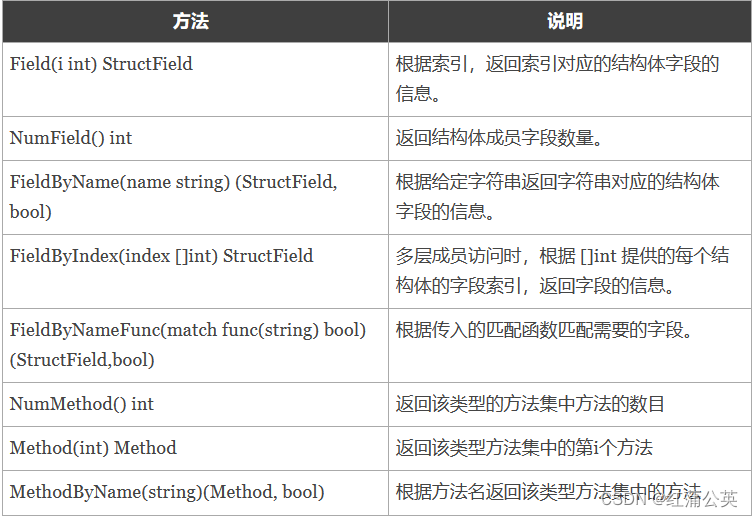
GoLong的学习之路(二十)进阶,语法之反射(reflect包)
这个是为了接上之前的语法篇的。按照我的学习计划,这里此时应该有一个小项目来做一个统合。但是吧,突然觉得,似乎也没必要。能学go的大部分肯定都是有其他语言的基础的。 接下来说反射 文章目录 反射介绍reflect包TypeOftype name和type kin…...

关于表单校验,:rules=“loginRules“
在写好validator相关的方法后,rule测试没有生效 <el-form ref"loginForm" :model"loginForm" :rules"loginRules" class"login-form" <el-form-item prop"username"> <el-input ref"usernam…...

统一消息分发中心设计
背景 我们核心业务中订单完成时,需要完成后续的连带业务,扣件库存库存、增加积分、通知商家等。 如下图的架构: 这样设计出来导致我们的核心业务和其他业务耦合,每次新增连带业务或者去掉连带业务都需要修改核心业务。 一方面&…...
前端项目导入vue和element
1.安装nodejs 下载链接https://cdn.npmmirror.com/binaries/node/v18.18.0/node-v18.18.0-x64.msi 进入cmd 命令行模式 管理员身份运行 输入 (node -v)能看到版本号 npm config set prefix "C:\Program Files\nodejs" 默认路径 npm config…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
