【数据结构】树与二叉树(六):二叉树的链式存储
文章目录
- 5.1 树的基本概念
- 5.1.1 树的定义
- 5.1.2 森林的定义
- 5.1.3 树的术语
- 5.1.4 树的表示
- 5.2 二叉树
- 5.2.1 二叉树
- 5.2.2 二叉树顺序存储
- 5.2.3 二叉树链接存储
- 特点
- C语言实现
5.1 树的基本概念
5.1.1 树的定义
- 一棵树是结点的有限集合T:
- 若T非空,则:
- 有一个特别标出的结点,称作该树的根,记为root(T);
- 其余结点分成若干个不相交的非空集合T1, T2, …, Tm (m>0),其中T1, T2, …, Tm又都是树,称作root(T)的子树。
- T 空时为空树,记作root(T)=NULL。
- 若T非空,则:
5.1.2 森林的定义
5.1.3 树的术语
- 父亲(parent)、儿子(child)、兄弟(sibling)、后裔(descendant)、祖先(ancestor)
- 度(degree)、叶子节点(leaf node)、分支节点(internal node)
- 结点的层数
- 路径、路径长度、结点的深度、树的深度
参照前文:【数据结构】树与二叉树(一):树(森林)的基本概念:父亲、儿子、兄弟、后裔、祖先、度、叶子结点、分支结点、结点的层数、路径、路径长度、结点的深度、树的深度
5.1.4 树的表示
- 【数据结构】树与二叉树(二):树的表示C语言:树形表示法、嵌套集合表示法、嵌套括号表示法 、凹入表示法
5.2 二叉树
5.2.1 二叉树
1. 定义
二叉树是一种常见的树状数据结构,它由结点的有限集合组成。一个二叉树要么是空集,被称为空二叉树,要么由一个根结点和两棵不相交的子树组成,分别称为左子树和右子树。每个结点最多有两个子结点,分别称为左子结点和右子结点。
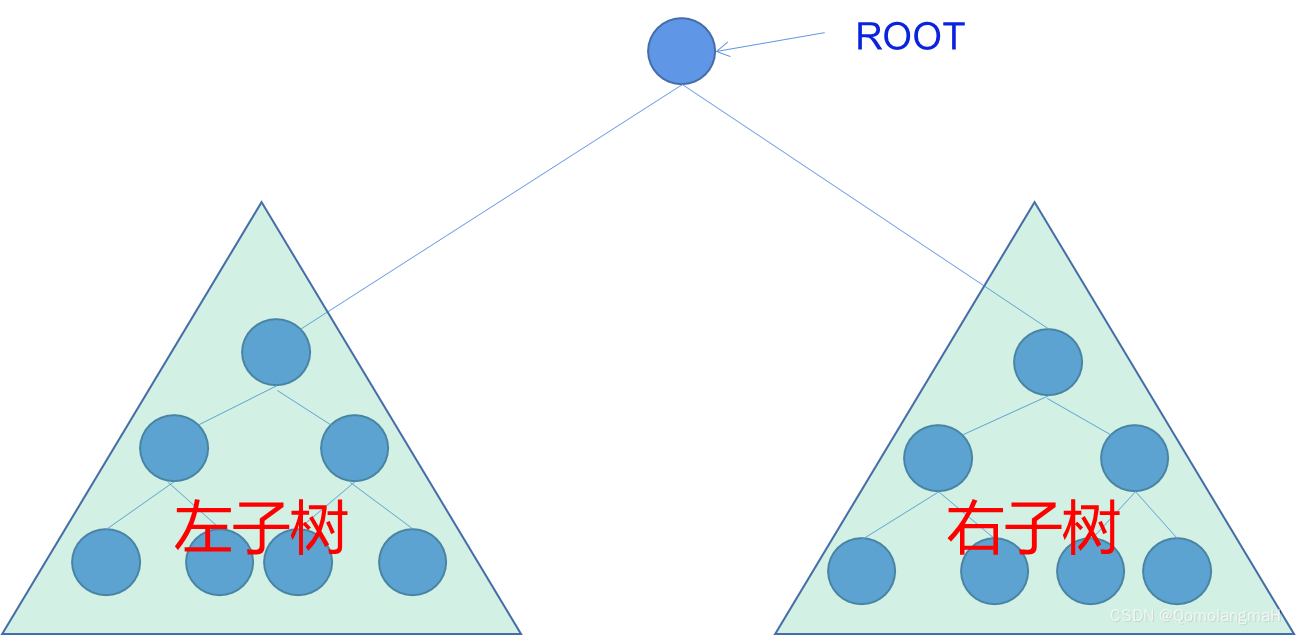
2. 特点
二叉树的特点是每个结点最多有两个子结点,并且子结点的位置是有序的,即左子结点在前,右子结点在后。这种有序性使得二叉树在搜索、排序等算法中有广泛的应用。
-
在二叉树中,根结点是整个树的起始点,通过根结点可以访问到整个树的其他结点。每个结点都可以看作是一个独立的二叉树,它的左子树和右子树也是二叉树。
-
二叉树可以是空树,也可以是只有根结点的树,或者是由多个结点组成的树。每个结点可以包含一个数据元素,以及指向左子结点和右子结点的指针。
-
二叉树的形状可以各不相同,它可以是平衡的或者不平衡的,具体取决于结点的分布情况。在二叉树中,每个结点的左子树和右子树都是二叉树,因此可以通过递归的方式来处理二叉树的操作。
3. 性质
引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。
引理5.2:高度为k的二叉树中至多有 2 k + 1 − 1 2^{k+1}-1 2k+1−1个结点,其中 k ≥ 0 k \geq 0 k≥0。
引理5.3:设T是由n个结点构成的二叉树,其中叶结点个数为 n 0 n_0 n0,度数为2的结点个数为 n 2 n_2 n2,则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1。
- 详细证明过程见前文:【数据结构】树与二叉树(三):二叉树的定义、特点、性质及相关证明
4. 满二叉树
5. 完全二叉树
- 满二叉树、完全二叉树性质及证明:【数据结构】树与二叉树(四):满二叉树、完全二叉树及其性质
5.2.2 二叉树顺序存储
二叉树的顺序存储是指将二叉树中所有结点按层次顺序存放在一块地址连续的存储空间中,详见:
【数据结构】树与二叉树(五):二叉树的顺序存储(初始化,插入结点,获取父节点、左右子节点等)
顺序存储方式的优点是节省了存储空间,同时访问结点也非常快速,因为可以通过数组索引直接访问结点,而不需要进行指针的跳转。然而,顺序存储方式也有一些限制:
-
空间浪费:对于非完全二叉树,顺序存储方式可能会浪费大量存储空间。因为顺序存储方式需要使用连续的存储空间来存储所有结点,而非完全二叉树中存在许多空缺的位置,这些位置将被浪费掉。
-
动态性差:顺序存储方式需要提前确定二叉树的最大结点个数,对于结点数不确定或者动态变化的情况下,顺序存储方式不太适用。如果二叉树的结点数超过了预先分配的存储空间,就需要重新分配更大的存储空间并进行数据迁移,这会增加额外的开销。
-
插入和删除操作复杂:对于顺序存储方式,插入和删除操作比较复杂。当需要插入或删除一个结点时,需要进行数据的移动和调整,以保持完全二叉树的性质。这会导致较高的时间复杂度和额外的操作开销。
因此,对于非完全二叉树或者需要频繁进行插入和删除操作的情况,链式存储方式更为灵活和高效。
5.2.3 二叉树链接存储
二叉树的链接存储系指二叉树诸结点被随机存放在内存空间中,结点之间的关系用指针说明。在链式存储中,每个二叉树结点都包含三个域:数据域(Data)、左指针域(Left)和右指针域(Right),用于存储结点的信息和指向子结点的指针。具体结点的结构如下所示:
struct BinaryTreeNode {DataType Data; // 数据域,存放结点的信息BinaryTreeNode* Left; // 左指针域,指向左子结点BinaryTreeNode* Right; // 右指针域,指向右子结点
};
在二叉树的链接存储中,存在一个指向根结点的指针,通常称为根指针。根指针用于访问整个二叉树。如果二叉树为空,根指针将被设置为NULL(即空指针)。
叶结点是没有子结点的结点,因此叶结点的左指针域和右指针域都会存放NULL,表示没有左子结点和右子结点。
在包含n个结点的二叉树的链接存储中,需要2n个指针域。其中,n-1个指针域用于指示结点的左子结点和右子结点,剩余的n+1个指针域为空。这是因为树中的每个结点(除了根结点)都有一个父结点,而父结点与子结点之间有两个指针域(左指针域和右指针域)相连,所以总共需要2n个指针域。但是根结点没有父结点,因此只有n-1个指针域用于指示结点的左子结点和右子结点。这个结论可以通过引理5.3(E = n-1)**来证明。
特点
- 每个结点通过指针域与其左子结点和右子结点建立联系,形成二叉树的结构。通过这种链接方式,可以方便地遍历和操作二叉树。
- 链式存储方式的优点是灵活性高,适用于各种类型的二叉树,无需提前确定结点个数,适用于动态变化的情况。同时,链式存储方式不要求连续的存储空间,每个结点可以在内存中的任意位置,通过指针的连接来表示结点之间的逻辑关系。
- 然而,链式存储方式也存在一些缺点。相比于顺序存储方式,链式存储需要额外的指针开销,每个结点都需要额外的指针域来存储指向子结点的指针。此外,访问结点需要通过指针的跳转,相对于顺序存储方式来说,可能会稍微降低访问效率。
C语言实现
#include <stdio.h>
#include <stdlib.h>// 二叉树结点的定义
struct Node {char data;struct Node* left;struct Node* right;
};// 创建新结点
struct Node* createNode(int data) {struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));if (newNode == NULL) {printf("Memory allocation failed!\n");exit(1);}newNode->data = data;newNode->left = NULL;newNode->right = NULL;return newNode;
}int main() {// 创建一棵二叉树struct Node* root = createNode('a');root->left = createNode('b');root->right = createNode('c');root->left->left = createNode('d');root->left->right = createNode('e');root->left->right->left = createNode('f');root->left->right->right = createNode('g');return 0;
}
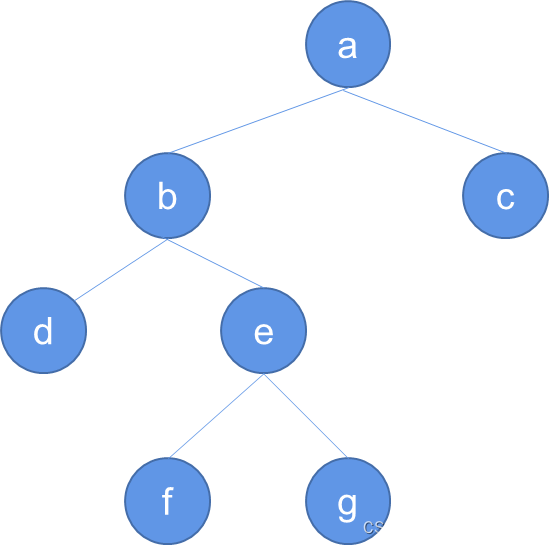
相关文章:

【数据结构】树与二叉树(六):二叉树的链式存储
文章目录 5.1 树的基本概念5.1.1 树的定义5.1.2 森林的定义5.1.3 树的术语5.1.4 树的表示 5.2 二叉树5.2.1 二叉树1. 定义2. 特点3. 性质引理5.1:二叉树中层数为i的结点至多有 2 i 2^i 2i个,其中 i ≥ 0 i \geq 0 i≥0。引理5.2:高度为k的二叉…...
)
后端Java日常实习生面试(2023年11月10日)
面试岗位为:Java 后端开发实习生 面试时长:30分钟 面试时间:2023年11月10日 首先介绍一下项目吧 这里介绍时有一个失误,没有主动把屏幕共享给打开,因为我在面试之前已经在 processon 上画好了项目的流程图…...

使用iperf3在macOS上进行网络性能测试
iperf3是一个用于测量网络性能的工具,它可以帮助你了解两台服务器之间的带宽和延迟。本博客将指导你在macOS上安装iperf3,并展示如何连接服务器进行网络性能测试。 步骤1:安装Homebrew 如果你尚未安装Homebrew,可以通过以下步骤…...

09-MySQL主从复制
01-主从复制原理 MySQL主从复制是一种用于实现数据备份、读写分离和扩展性的技术。它基于二进制日志(Binary Log)来将主数据库上的更改操作同步到一个或多个从数据库。 MySQL主从复制的基本原理如下: 主服务器(Master࿰…...

virtualBox虚拟机局域网访问配置
在VirtualBox中,桥接网络是一种网络连接类型,它允许虚拟机连接到物理网络上的路由器或交换机,在物理网络上获得独立的网络地址和访问权限。 一、设置VirtualBox桥接网络的步骤: 打开VirtualBox软件,并选择你想要配置…...

IDEA高效编程快捷键
IDEA高效编程快捷键 for循环快捷键 快速生成for循环 foriTABfor (int i 0; i < ; i) {}在for循环中使用索引 iterTABfor (String s : list) {}在for循环中进行if条件判断 ifnTABif (list null) {} soutTAB快捷键 System.out.println();psfEnter快捷键 p…...

nginx实现vue和后端的双机负载
nginx配置文件,项目是前后端分离的,前端vue,后端springboot 前端使用nginx实现双机负载,前端的访问端口是95280,后端2个服务实例的端口分部为9098,9099 nginx.conf的配置文件 #user root; worker_processes 1;#err…...

ARMday03(寄存器读写、栈、程序状态寄存器、软中断和异常、混合编程)
单寄存器内存读写指令 将一个寄存器中的数值写入到内存,或者从内存中读取数据放在某一个指定寄存器中 指令码和功能 1.向内存中写: str{条件码} 目标寄存器,[目标地址]:将目标寄存器的4字节数值写入到目标地址为首地址的空间中 strh{条件码…...
Excel中功能区的存放位置很灵活,可以根据需要隐藏或显示
在这个简短的教程中,你将找到5种快速简单的方法来恢复Excel功能区,以防丢失,并学习如何隐藏功能区,为工作表腾出更多空间。 功能区是Excel中所有操作的中心点,也是大多数可用功能和命令所在的区域。你觉得功能区占用了你太多的屏幕空间吗?没问题,只需单击鼠标,它就被隐…...
HelloGitHub 社区动态,开启新的篇章!
今天这篇文章是 HelloGitHub 社区动态的第一篇文章,所以我想多说两句,聊聊为啥开启这个系列。 我是 2016 年创建的 HelloGitHub,它从最初的一份分享开源项目的月刊,现如今已经成长为 7w Star 的开源项目、1w 用户的开源社区、全网…...
【学术综述】-如何写出一篇好综述-写好综述要注意的问题
文章目录 1.前置1.1 SSD 的结构1.2 FTL的架构和作用 2 动机-why?3 做了什么【做了哪些方面的survey】?4 背景知识【上下文】5 研究的问题6 每个问题对应的解决方案 从昨天晚上【2023.11.09 22:00】到今天22:29的,花了一天的时间在读这篇surve…...
ClickHouse介绍和使用
ClickHouse介绍和使用 1. 简介2. ClickHouse特点3. 数据类型3.1. 整型3.2. 浮点型3.3. Decimal型3.4. 布尔型3.5. 字符串3.6. 枚举类型3.7. 时间类型 4. 表引擎4.1. TinyLog4.2. Memory4.3. MergeTree4.3.1. partition by分区(可选)4.3.2. primary key 主…...

数码管动态扫描
/*----------------------------------------------- 内容:数码管使用动态扫描显示,所以可以同时看到数码管同时显示数字或者字符。 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不…...
Webpack 中 loader 的作用是什么?常用 loader 有哪些?
说说webpack中常见的Loader?解决了什么问题?- 题目详情 - 前端面试题宝典 1、loader 是什么 loader是 webpack 最重要的部分之一。 通过使用不同的 loader,我们能够调用外部的脚本或者工具,实现对不同格式文件的处理。 loader…...

c#,字段和属性的区别
c#,string test和string test{ges;set;}有什么区别 在C#中,string test和string test { get; set; }表达了两种不同的成员声明,它们在类中的作用和访问方式是不同的。 string test: 这是一个字段(field)声明。它声明了一个类型…...
ideal一键部署SpringBoot项目jar包到服务器
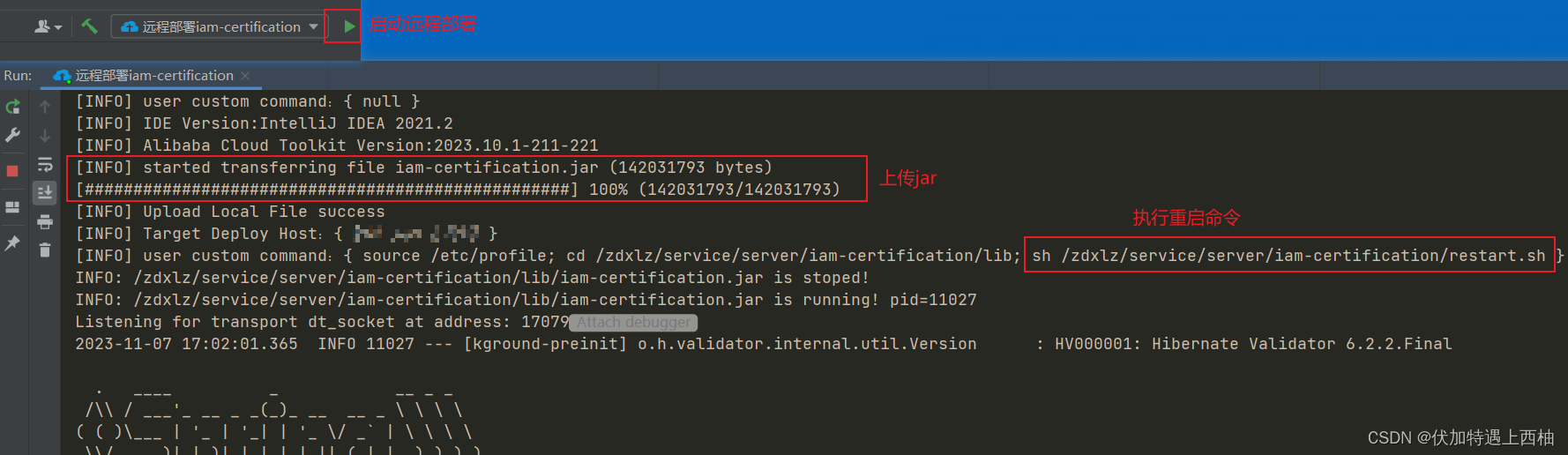
一 简介 我们在开发环境部署项目一般通过ideal将项目打包成jar包,然后连接linux服务器,将jar手动上传到服务中,重启服务。 概括的说流程是这样的: 本地打包->上传到服务器->kill掉以前的服务->重新启动jar包服务 每次总是循环这一…...
宝塔部署QQ机器人,提示OpenSSL 1.0.2k-fips 26 Jan 2017
1、报错预览 Traceback (most recent call last):File "/www/wwwroot/python/bot-one/main.py", line 5, in <module>import requestsFile "/www/wwwroot/python/bot-one/343ae0eb0d491a10a1a00c0621b03ed0_venv/lib/python3.9/site-packages/requests/_…...

K8S篇之简述K8S底层原理
k8s底层原理 Kubernetes(简称k8s)是一个开源的容器编排平台,它可以自动化地部署、扩展和管理容器化应用程序。 Kubernetes 底层原理是其能够实现这些功能的关键。 1 节点和控制平面 Kubernetes 由两个主要组件组成:节点Node和控…...
打开ps提示,计算机中丢失d3dcompiler_47.dll怎么解决?
“d3dcompiler_47.dll丢失5个解决办法”。相信很多同事在工作或者娱乐的过程中,都遇到过这个错误提示。那么,究竟什么是d3dcompiler_47.dll文件?为什么会丢失呢?又该如何解决这个问题呢?接下来,我将为大家详…...

torch.mm
torch.mm(input, mat2, *, outNone) → Tensor执行矩阵input和mat2的矩阵乘法运算。 如果input是(nm)张量,mat2是(mp)张量,out将是(n x p)张量。 input(张量࿰…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
