【学习笔记】NOIP爆零赛7
结论专场,结果被踩暴了
青鱼和序列
赛时的做法是,维护∑ai×i\sum a_i\times i∑ai×i的取值,发现只和最后一次操作222的位置有关,于是递推O(n)O(n)O(n)解决。
赛后发现还有更神奇的结论 第二个结论是,第一次进行操作222过后,aaa序列变成回文的了,所以这之后1,21,21,2操作就是等价的了。
这两个结论单独来看都很容易发现。不过接下来这个结论可能不容易看出:只要进行了操作222,那么最后的结果就是一定的。事实上这不难从前222个结论中看出。不过如果打表还是很容易看出的
看来我猜结论的功底还是太菜了,还是要多尝试啊
青鱼和怪兽
猜了一个结论,直接二分答案就可以解决。
同样不难通过打表证明这个结论是正确的
青鱼和区间
垃圾题解写的像shit一样,真就谜语人呗
这个结论太小,以至于我看不见
这道题的思维量还是非常高的,不过nknknk这波玄学过题确实佩服。。。
我是joker,以为这道题转移比较难想,最后发现我连计数的对象都没搞清楚
如果不先入为主而是尝试推一下结论的话这道题还是可以分析的吧,但是最后那一步凭考场上的我是无论如何也推不出来的
首先最直白的翻译是,设SiS_iSi表示覆盖iii位置的区间的集合,那么合法的条件等价于SiS_iSi互不相同。
然后有一个结论:不存在i1<i2<j1<j2i_1<i_2<j_1<j_2i1<i2<j1<j2,使得Si1=Sj1≠Si2=Sj2S_{i_1}=S_{j_1}\ne S_{i_2}=S_{j_2}Si1=Sj1=Si2=Sj2
这个结论的正确性其实挺显然的,但是当时我没往这方面想,而是直接去刚dpdpdp了,现在想来确实是不明智的行为
那么我们把相同等价类的位置提出来,记作区间[li:ri][l_i:r_i][li:ri],那么这些区间要么包含要么不相交,这个结构就非常显而易见了:我们可以把原序列划分成若干个连续段,同时不存在两个不属于同一个连续段的i,ji,ji,j使得Si=SjS_i=S_jSi=Sj。这个性质也等价于什么呢,对于询问区间[i:j][i:j][i:j],要么i,ji,ji,j在同一段中,要么[i:j][i:j][i:j]不能制造断点,也就是说[i:j][i:j][i:j]恰好是若干完整的段拼起来的。
现在我们只差最后一步:如何对这些若干不相交的[li:ri][l_i:r_i][li:ri]计数?
我竟就倒在了这里。。。
考虑一个普通至极的思路:正难则反。也就是说,我们减去分出来的段数<n<n<n的方案数。那么我们考虑,假设分成了jjj段,根据前面的观察,我们要把这分出来的jjj段区分出来,然后对于长度为lll的一段,我们需要注意端点是不能包括在区间中的,因此有(l−2)(l−1)2\frac{(l-2)(l-1)}{2}2(l−2)(l−1)个可选择的区间,方案数为2(l−2)(l−1)22^{\frac{(l-2)(l-1)}{2}}22(l−2)(l−1)。
有了上述动机,我们设dpidp_idpi表示长度为iii的答案,有转移式:dpi=2i(i+1)2−∑j<idpjfi,jdp_i=2^{\frac{i(i+1)}{2}}-\sum_{j<i}dp_jf_{i,j}dpi=22i(i+1)−∑j<idpjfi,j,其中fi,jf_{i,j}fi,j表示把iii分成jjj段的所有方案的系数和。
复杂度O(n3)O(n^3)O(n3)。可以用多项式工业优化到O(npoly(n))O(n\text{poly}(n))O(npoly(n)),但是有点复杂并且我不太懂所以就咕了
这就是天才和凡人的差距吗
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define ll long long
#define pb push_back
#define fi first
#define se second
using namespace std;
const int N=305;
int n,mod;
ll pw[N*N],dp[N][N],res[N];
void add(ll &x,ll y){x=(x+y)%mod;
}
int main(){cin>>n>>mod;pw[0]=1;for(int i=1;i<=n*n;i++)pw[i]=pw[i-1]*2%mod;dp[0][0]=1;for(int i=0;i<n;i++){for(int j=0;j<=i;j++){if(dp[i][j]){for(int k=1;k<=n-i;k++){add(dp[i+k][j+1],dp[i][j]*pw[(k-1)*(k-2)/2]);}}}}for(int i=1;i<=n;i++){res[i]=pw[i*(i+1)/2];for(int j=1;j<i;j++){res[i]=(res[i]-res[j]*dp[i][j])%mod;}}cout<<(res[n]+mod)%mod;
}
青鱼和游戏
考场上爆蛋了
这题爆蛋有两个原因:一是确实不会做,二是t3t3t3确实被卡住了
说白了就是太菜了
相关文章:

【学习笔记】NOIP爆零赛7
结论专场,结果被踩暴了 青鱼和序列 赛时的做法是,维护∑aii\sum a_i\times i∑aii的取值,发现只和最后一次操作222的位置有关,于是递推O(n)O(n)O(n)解决。 赛后发现还有更神奇的结论 第二个结论是,第一次进行操作…...

一文读懂账号体系产品设计
一、账号体系的概念及价值账号体系是用户在各平台上的通行证。平台给与用户可持续的服务,用户在平台上获取价值,中间的媒介,便是账号体系。阿境将其理解为维系用户与平台之间的枢纽。注:本文中,账号账户,二…...
从“入门”到“专家”,一份3000字完整的性能测试体系的知识分享
随着科技的飞速发展,软件产品广泛应用于各个行业领域,人们对计算机和网络的依赖性越来越大,对新奇事物也越来越感兴趣,成千上万的用户活跃在庞大的网络系统中,这给提供服务的系统带来严重的负荷,"高并…...

构建对话机器人:Rasa3安装和基础入门
在开源对话机器人中,Rasa社区很活跃,在国内很多企业也在使用Rasa做对话机器人,有rasa开发经验的往往是加分项。 当年实习的时候接触到了Rasa,现在工作中也使用Rasa,因此,写写一些经验文档,有助后…...
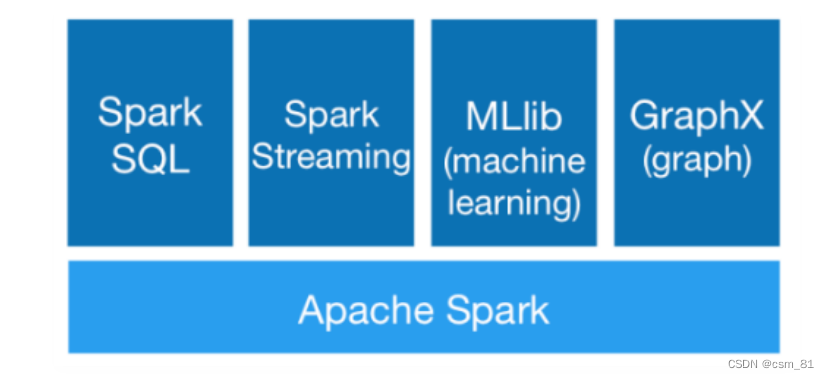
Spark计算框架入门笔记
Spark是一个用于大规模数据处理的统一计算引擎 注意:Spark不仅仅可以做类似于MapReduce的离线数据计算,还可以做实时数据计算,并且它还可以实现类似于Hive的SQL计算,等等,所以说它是一个统一的计算引擎 既然说到了Spar…...

入职数据分析公认的好书|建议收藏
众所周知,数据分析经常出现在我们的日常生活中,各行各业都需要数据分析。可你知道什么是数据分析?它在企业里到底扮演什么角色?以及如果我们自己也想拥有数据分析的能力,以便更好的满足数据分析的需求,我们…...

Linux查找文件和目录,重定向输出 ,系统默认运行级别的查看和设置理论和练习
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

Redis源码---键值对中字符串的实现,用char*还是结构体
目录 前言 为什么 Redis 不用 char*? char* 的结构设计 操作函数复杂度 SDS 的设计思想 SDS 结构设计 SDS 操作效率 紧凑型字符串结构的编程技巧 小结 前言 对于 Redis 来说,键值对中的键是字符串,值有时也是字符串在 Redis 中写入一…...

算法 - 剑指Offer 表示数值的字符串
题目 请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。 数值(按顺序)可以分成以下几个部分: 若干空格 一个 小数 或者 整数 (可选)一个 ‘e’ 或 ‘E’ ,后面跟着一个 …...
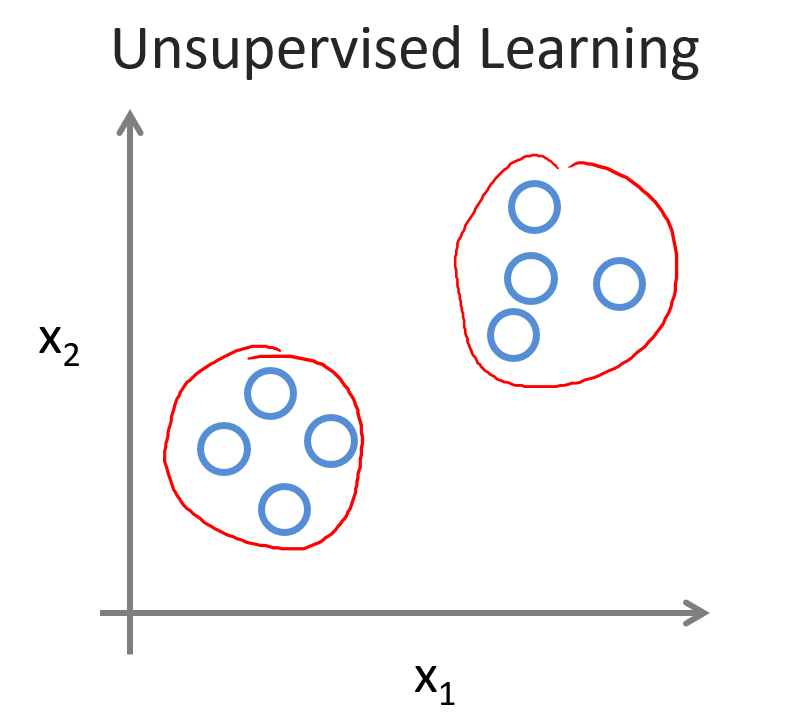
初识机器学习
监督学习与无监督学习supervised learning:监督学习,给出的训练集中有输入也有输出(标签)(也可以说既有特征又有目标),在此基础上让计算机进行学习。学习后通过测试集测试给相应的事物打上标签。…...
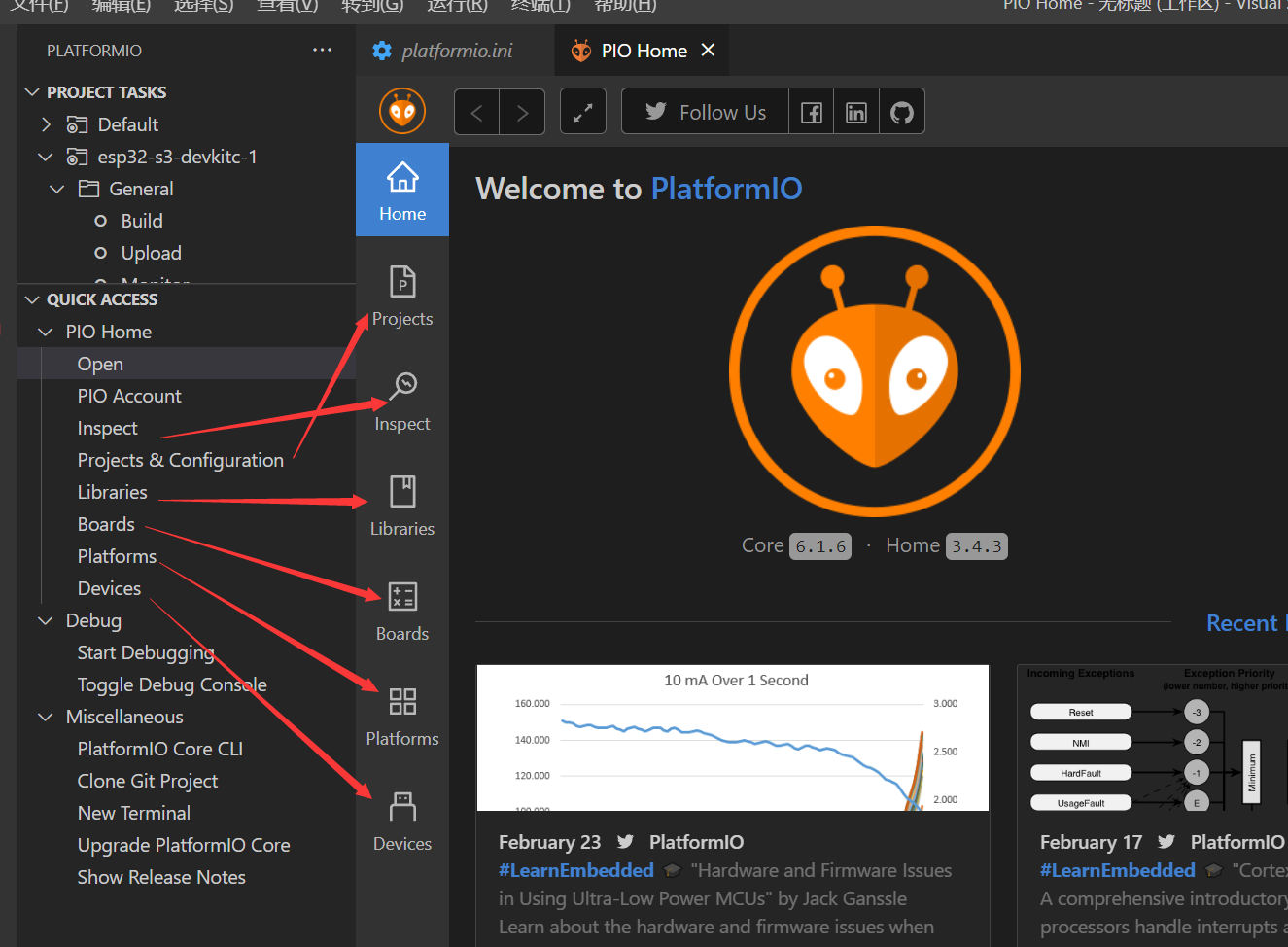
VsCode安装PlatformIO 开发ESP arduino,买的板子或者随便ESP,PlatformIO添加Board(不是自定义Board)
这次主要记录怎么给新建选板子的时候没有的板子下程序 我这里是一块 WiFi Kit 32 (V3) PlatformIO里面只有到V2 先从头开始,安装PlatformIO 安装PlatformIO 直接搜索安装 安装有时候会比较慢,左侧出现蚂蚁图标之后点击会显示 右下角会提示正在安…...

golang 复杂数据结构解析
[{"key":"15275771","pack":{"1":[{"name":"消息配置","id":15275771,"version":1,"createUser":"molaifeng","data":"test"}]},"callback&qu…...

不怕被AirTag跟踪?苹果Find My技术越来越普及
苹果的 AirTag 自推出以来,如何有效遏制用户用其进行非法跟踪,是摆在苹果面前的一大难题。一家为执法部门制造无线扫描设备的公司近日通过 KickStarter 平台,众筹了一款消费级产品,可帮助用户检测周围是否存在追踪的 AirTag 等设备…...
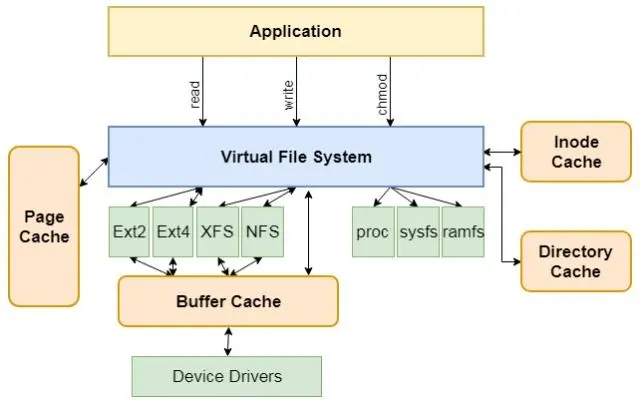
Linux驱动中的open函数是如何从软件打通硬件呢?
一、前言 打开文件是Linux系统中最基本的操作之一,open函数可以实现打开文件的功能。下面我将为您介绍open函数打通上层到底层硬件的详细过程。 二、open函数打通软硬件介绍 open函数是系统调用中的一种,其原型定义在头文件unistd.h中: #…...

Java 基础语法
Java 是一门广泛使用的编程语言,由于其简单易学和可移植性,已成为开发 Web 应用程序、移动应用程序、桌面应用程序以及企业级应用程序的首选语言之一。在本文中,我们将探讨 Java 的基础语法,包括变量、数据类型、运算符、控制流等…...
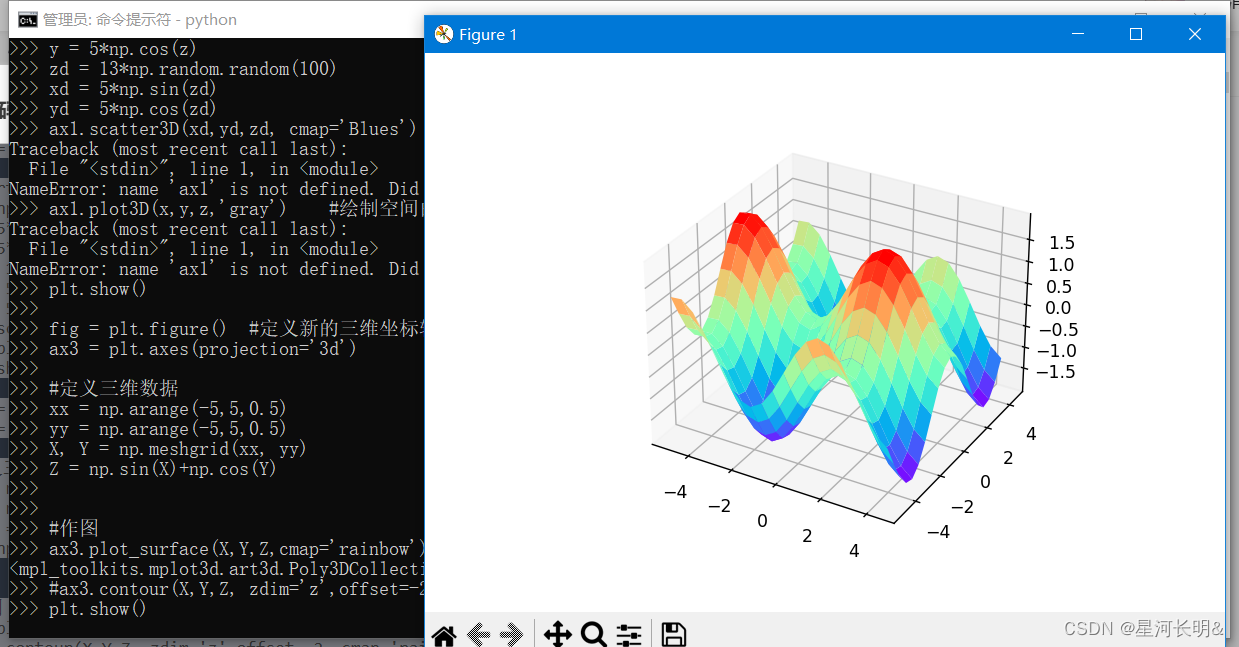
python下如何安装并使用matplotlib(画图模块)
在搜索命令中输入cmd,以管理员身份运行。 输入以下命令,先对pip安装工具进行升级 pip install --upgrade pip 升级完成 之后使用pip安装matplotlib pip install matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple 也可以使用pycharm来安装matp…...

系统分析师---计算机网络思维导图
TCP、IP协议簇(4星) 传输协议:TCP有连接、可靠、有回应机制、三次握手基于TCP的应用层协议:POP3:邮件收取,默认端口110SMTP:邮件发送,默认端口25FTP:文件传输协议&#…...

算法练习(七)数据分类处理
一、数据分类处理 1、题目描述: 信息社会,有海量的数据需要分析处理,比如公安局分析身份证号码、 QQ 用户、手机号码、银行帐号等信息及活动记录。采集输入大数据和分类规则,通过大数据分类处理程序,将大数据分类输出…...

nohup ./startWebLogic.sh >out.log 2>1 解析
在启动weblogic的时候我们经常看到如下的命令: nohup ./startWebLogic.sh >out.log 2>&1 & 从09年开始用weblogic到现在已经过去3年多了 ,今天终于将该命令理解清楚了。 其中 0、1、2分别代表如下含义: 0 – stdin (standa…...
)
OpenCV 坡度计算(基于DEM,C++版本)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 假设一个点位于曲面 z = f ( x , y ) z=f(x,y) z=...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
