当前位置： 首页 > news >正文

【OpenHarmony内核】Harmony内核之线程操作函数（二）

news 2026/2/8 15:45:42

文章目录

  • 前言
  • 一、获取线程优先级
  • 二、转交控制运行权
  • 三、挂起线程
    • 3.1 线程的挂起是什么意思？
    • 3.2 函数介绍
  • 四、恢复线程
  • 五、分离指定的线程
    • 5.1 分离线程是什么意思
    • 5.2 函数介绍
  • 六、等待线程终止运行
  • 七、终止当前线程的运行
  • 八、终止指定线程的运行
  • 九、获取活跃线程数
  • 总结

前言

OpenHarmony是一个开源的分布式操作系统，具有强大的任务管理功能。任务是操作系统的核心组成部分，负责执行不同的功能和操作。在本文中，我们将深入探讨OpenHarmony内核的任务管理功能，包括任务的创建、调度、挂起和删除等方面。

任务是操作系统中的基本执行单元，OpenHarmony的任务管理系统允许开发者创建多个并发任务，并有效地进行调度和管理。任务的管理对于实现多任务处理、资源共享和响应用户需求至关重要。

相关文章：

【OpenHarmony内核】Harmony内核之线程操作函数（二）

文章目录 前言一、获取线程优先级二、转交控制运行权三、挂起线程3.1 线程的挂起是什么意思？3.2 函数介绍四、恢复线程五、分离指定的线程5.1 分离线程是什么意思5.2 函数介绍六、等待线程终止运行七、终止当前线程的运行八、终止指定线程的运行九、获取活跃线程数总结前言 O…...

编程日记 2023/11/11 9:22:21

二十五、W5100S/W5500+RP2040树莓派Pico＜Modebus TCP Server示例＞

文章目录 1 前言2 简介2 .1 什么是Modbus TCP？2.2 Modbus TCP指令介绍2.3 请求数据过程2.4 Modbus TCP协议优点2.5 Modbus TCP应用场景 3 WIZnet以太网芯片4 Modbus TCP示例概述以及使用4.1 流程图4.2 准备工作核心4.3 连接方式4.4 主要代码概述4.5 结果演示 5 注意…...

编程日记 2023/11/11 9:21:20

Android画个圆点状态灯

1、创建一个 XML 文件在 res/drawable 目录下&#xff08;默认为黑色&#xff09; <?xml version"1.0" encoding"utf-8"?> <shape xmlns:android"http://schemas.android.com/apk/res/android"android:shape"oval"><…...

编程日记 2023/11/11 9:20:19

高性能网络编程 - 解读3种线程模型

文章目录 Pre线程模型1&#xff1a;传统阻塞 I/O 服务模型线程模型2&#xff1a;Reactor 模式Reactor 模式的基本设计思想Reactor 模式中的关键组成3种典型实现单 Reactor 单线程单 Reactor 多线程主从 Reactor 多线程 小结 线程模型3&#xff1a;Proactor 模型 Pre 高性能网络…...

编程日记 2023/11/11 9:19:18

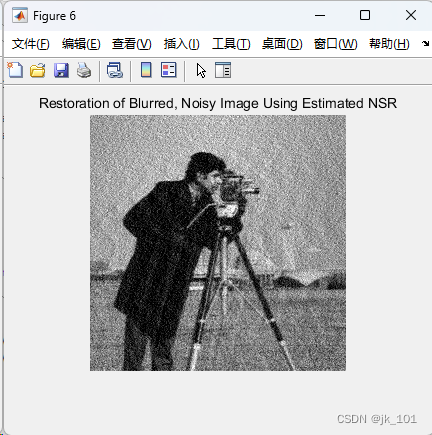
MATLAB中deconvwnr函数用法

目录 语法 说明 示例 使用 Wiener 滤波对图像进行去模糊处理 deconvwnr函数的功能是使用 Wiener 滤波对图像进行去模糊处理。 语法 J deconvwnr(I,psf,nsr) J deconvwnr(I,psf,ncorr,icorr) J deconvwnr(I,psf) 说明 J deconvwnr(I,psf,nsr) 使用 Wiener 滤波算法对…...

编程日记 2023/11/11 9:18:17

赛宁网安入选国家工业信息安全漏洞库（CICSVD）2023年度技术组成员单

近日&#xff0c;由国家工业信息安全发展研究中心、工业信息安全产业发展联盟主办的“2023工业信息安全大会”在北京成功举行。 会上&#xff0c;国家工业信息安全发展研究中心对为国家工业信息安全漏洞库&#xff08;CICSVD&#xff09;提供技术支持的单位授牌表彰。北京赛宁…...

编程日记 2023/11/11 9:17:16

Git系列之Git集成开发工具及git扩展使用

&#x1f389;&#x1f389;欢迎来到我的CSDN主页&#xff01;&#x1f389;&#x1f389; &#x1f3c5;我是君易--鑨&#xff0c;一个在CSDN分享笔记的博主。&#x1f4da;&#x1f4da; &#x1f31f;推荐给大家我的博客专栏《Git实战开发》。&#x1f3af;&#x1f3af; &a…...

编程日记 2023/11/11 9:16:14

selenium headless 无头模式慢

selenium设置headlessTrue发现非常慢&#xff0c;headlessFalse要快很多。 最后测试发现升级到selenium最新版本&#xff0c;selenium4.15.2。设置--headlessnew&#xff0c;解决了&#xff0c;速度正常了。 新版selenium有了两种headless模式&#xff0c;参见&#xff1a;He…...

编程日记 2023/11/11 9:15:14

快速修复因相机断电导致视频文件打不开的问题

3-5 本文主要解决因相机突然断电导致拍摄的视频文件打不开的问题。 在日常工作中&#xff0c;有时候需要使用相机拍摄视频&#xff0c;比如现在有不少短视频拍摄的需求&#xff0c;如果因电池突然断电的原因&#xff0c;导致拍出来的视频播放不了&#xff0c;这时候就容易出大…...

编程日记 2023/11/11 9:14:13

Ceph 笔记， ssh写入缓存

硬件建议 — Ceph 文档 写入缓存 企业级 SSD 和 HDD 通常包括断电保护功能&#xff0c;包括 在运行时断电时确保数据耐久性&#xff0c;以及 使用多级缓存来加快直接或同步写入速度。这些设备 可以在两种缓存模式之间切换 -- 刷新到的易失性缓存 具有 fsync 的持久性媒体&a…...

编程日记 2023/11/11 9:13:12

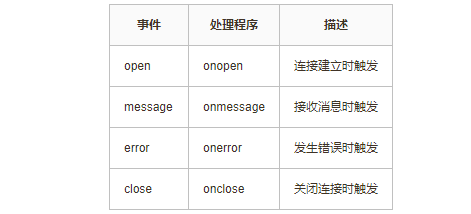
WebSocket魔法师：打造实时应用的无限可能

1、背景 在开发一些前端页面的时候&#xff0c;总是能接收到这样的需求&#xff1a;如何保持页面并实现自动更新数据呢&#xff1f;以往的常规做法&#xff0c;是前端使用定时轮询后端接口&#xff0c;获取响应后重新渲染前端页面&#xff0c;这种做法虽然能达到类似的效果&…...

编程日记 2023/11/11 9:12:11

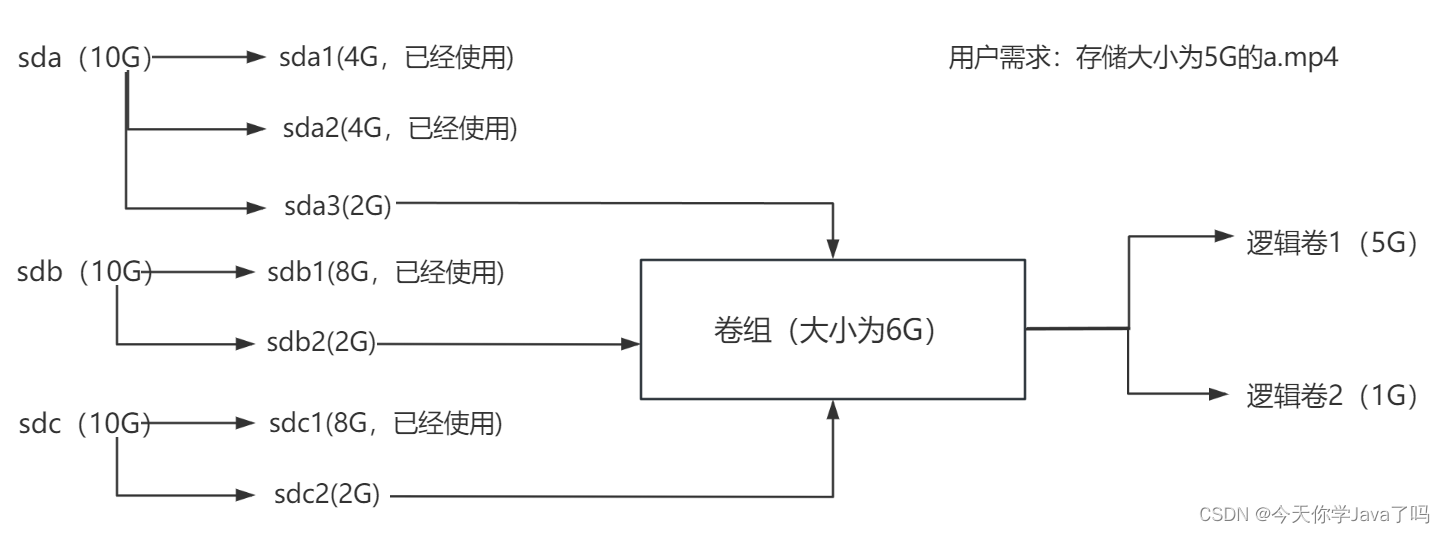
网络运维Day06-补充

文章目录 RAID磁盘阵列RAID0条带模式RAID1镜像模式RAID5高性价比模式RAID01RAID10 逻辑卷一块磁盘的使用流程逻辑卷的使用流程 制作逻辑卷步骤一&#xff1a;添加硬盘步骤二&#xff1a;分区规划步骤三&#xff1a;制作物理卷步骤四&#xff1a;制作卷组步骤五&#xff1a;制作…...

编程日记 2023/11/11 9:11:11

openssl+SM2开发实例一（含源码）

一、SM2算法介绍 SM2&#xff08;国密算法2&#xff09; 是中国国家密码管理局&#xff08;CNCA&#xff09;颁布的椭圆曲线密码算法标准&#xff0c;属于非对称加密算法。它基于椭圆曲线离散对数问题&#xff0c;提供了安全可靠的数字签名、密钥交换和公钥加密等功能。SM2被设…...

编程日记 2023/11/11 9:10:10

操作系统 | 编写内核

&#x1f308;个人主页&#xff1a;Sarapines Programmer&#x1f525; 系列专栏&#xff1a;《操作系统实验室》&#x1f516;少年有梦不应止于心动&#xff0c;更要付诸行动。 目录结构 1. 操作系统实验之编写内核 1.1 实验目的 1.2 实验内容 1.3 实验步骤 1.4 实验过程 …...

编程日记 2023/11/11 9:07:07

Rust逆向学习 (4)

Reverse for Struct Rust中的结构体是一个重要的内容&#xff0c;由于Rust中没有类的概念&#xff0c;因此其他编程语言中的封装、继承、多态与Rust中的表现都有较大差异。 我们使用参考书中的一个示例开始进行分析。 Struct 初始化 struct User {username: String,email: …...

编程日记 2023/11/11 9:06:06

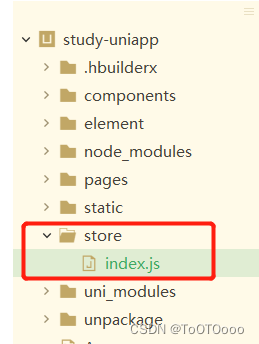
uniapp vue2 vuex 持久化

1.vuex的使用 一、uniapp中有自带vuex插件&#xff0c;直接引用即可 二、在项目中新建文件夹store,在main.js中导入 在根目录下新建文件夹store,在此目录下新建index.js文件 index.js import Vue from vueimport Vuex from vuexVue.use(Vuex)const store new Vuex.Store(…...

编程日记 2023/11/11 9:05:05

【媒体邀约】媒体宣传——企业成长的催化剂

传媒如春雨&#xff0c;润物细无声&#xff0c;大家好&#xff0c;我是51媒体网胡老师。 媒体宣传是企业成长的催化剂&#xff0c;它在各种方面对企业的成功和发展起到了关键作用。 1. 曝光和知名度&#xff1a; 媒体宣传可以将企业和其产品或服务推向广泛的受众&#xff0c;…...

编程日记 2023/11/11 9:04:04

ansible问题排查

拷贝模板时报错&#xff1a;AnsibleError: template error while templating string: Missing end of comment tag. 原因 shell脚本中地{#和jinja中的语法comment tag相同&#xff0c;而且只有一半&#xff0c;导致无法渲染导致。 解决 在有语法冲突的地方使用组合标签{% r…...

编程日记 2023/11/11 9:03:02

7天入门python系列之第四天python数据结构

第3天主要是学习Python的函数和模块 编者打算开一个python 初学主题的系列文章&#xff0c;用于指导想要学习python的同学。关于文章有任何疑问都可以私信作者。对于初学者想在7天内入门Python&#xff0c;这是一个紧凑的学习计划。但并不是不可完成的。第四天开始python 数据…...

编程日记 2023/11/11 9:02:01

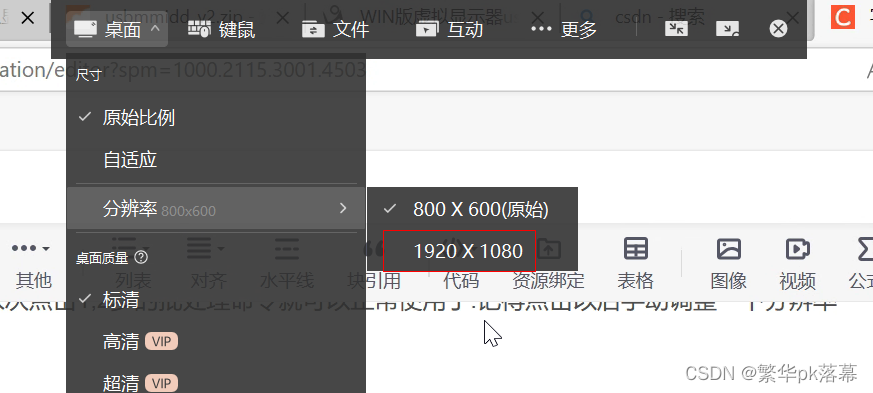
远程电脑未连接显示器时分辨率太小的问题处理

背景&#xff1a;单位电脑显示器坏了&#xff0c;使用笔记本通过向日葵远程连接&#xff0c;发现分辨率只有800*600并且不能修改&#xff0c;网上找了好久找到了处理方法这里记录一下&#xff0c;主要用到的是一个虚拟显示器软件usbmmidd_v2 1)下载usbmmidd_v2 2&#xff09;…...

编程日记 2023/11/11 9:01:00

Psychopy音频的使用

Psychopy音频的使用 本文主要解决以下问题&#xff1a; 指定音频引擎与设备&#xff1b;播放音频文件 本文所使用的环境&#xff1a; Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

编程新知 2026/1/31 15:09:31

04-初识css

一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

编程新知 2026/1/29 17:54:05

UR 协作机器人「三剑客」：精密轻量担当（UR7e）、全能协作主力（UR12e）、重型任务专家（UR15）

UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中&#xff0c;UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化&#xf…...

编程新知 2026/2/2 2:47:37

深入浅出深度学习基础：从感知机到全连接神经网络的核心原理与应用

文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么&#xff1f;1.1.2 感知机的工作原理 1.2 感知机的简单应用&#xff1a;基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

编程新知 2026/1/26 13:29:00

Mysql8 忘记密码重置，以及问题解决

1.使用免密登录 找到配置MySQL文件&#xff0c;我的文件路径是/etc/mysql/my.cnf&#xff0c;有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

编程新知 2026/1/9 8:59:09

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用

中达瑞和自2005年成立以来&#xff0c;一直在光谱成像领域深度钻研和发展&#xff0c;始终致力于研发高性能、高可靠性的光谱成像相机&#xff0c;为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

编程新知 2025/12/31 17:08:10

渗透实战PortSwigger靶场：lab13存储型DOM XSS详解

进来是需要留言的&#xff0c;先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码&#xff0c;输入的<>当成字符串处理回显到页面中&#xff0c;看来只是把用户输…...

编程新知 2026/2/4 18:11:56

Matlab实现任意伪彩色图像可视化显示

Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中&#xff0c;如何展示好看的实验结果图像非常重要&#xff01;&#xff01;&#xff01; 1、灰度原始图像 灰度图像每个像素点只有一个数值&#xff0c;代表该点的​​亮度&#xff08;或…...

编程新知 2026/2/7 2:14:33

向量几何的二元性：叉乘模长与内积投影的深层联系

在数学与物理的空间世界中&#xff0c;向量运算构成了理解几何结构的基石。叉乘&#xff08;外积&#xff09;与点积&#xff08;内积&#xff09;作为向量代数的两大支柱&#xff0c;表面上呈现出截然不同的几何意义与代数形式&#xff0c;却在深层次上揭示了向量间相互作用的…...

编程新知 2026/2/2 7:32:54

【题解-洛谷】P10480 可达性统计

题目&#xff1a;P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图&#xff0c;分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M&#xff0c;接下来 M M M 行每行两个整数 x , y x,y x,y&#xff0c;表示从 …...

编程新知 2025/12/15 8:11:23