算法--数据结构
这里写目录标题
- 本节内容
- 链表与邻接表
- 链表
- 主要思想
- 链表操作
- 初始化+在head结点后面插入
- 普通插入
- 删除操作
- 例子
- 双链表(双向循环链表)
- 主要思想
- 操作
- 初始化+双向插入
- 删除第k个点
- 邻接表
- 主要思想
- 栈和队列
- 栈
- 主要思想
- 主要操作
- 队列
- 主要思想
- 操作
- 单调栈与单调队列
- 单调栈
- 主要思想
- 例题
- 单调队列
- 主要思想
- 例题
- 二级目录
- 二级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
本节内容

链表与邻接表
链表
主要思想

因为用真正的链表来写算法的话 会new很多东西 而new的过程是非常慢的
所以我们要用数组来写链表
如上图 链表分为单链表和双链表 单链表主要是邻接表 主要作用是存储图和树
e[]数组用来存储各个结点的val值 而ne[]数组用来存储各个结点的next指针 而表示在数组里就是存储下一个结点的数组下标
最后的空地址用-1表示
head表示指向头结点的指针 实际上就是头结点的下标
!!所有的结点都在e[]数组里 但是他们的排序不是按照e[]的下标按照顺序连续排序的 他们的排序是一个链表 存在ne[]数组里
e[k] 是指下标为k的e[]数组中的值 也就是在e[]数组中 下标为k的值
ne[k] 是指在e[]数组中下标为k的结点 下一个结点在e[]数组中的位置(下标)

同时会定义一个int变量idx 存储当前操作的点的下标 实质上发挥着指针的作用
他会指针一个e[]数组中 最新的可用的位置 用来新建一个结点
链表操作
初始化+在head结点后面插入

初始化就是将head改为-1 意思是head指向-1位置的空间 也就是空指针
然后idx可以更新为0 因为e[]数组中第一个可用位置就是下标为0的位置
插入
首先新建结点 e[idx]=x
之后next域指向头结点 ne[idx]=head
因为head存储的就是第一个数据的下标
之后将head指向新插入的结点 head=idx
最后idx后移 更新最新的可操作的位置的下标
普通插入

将x插入到下标是k的结点的后面
删除操作


注意中括号里就是存储的下标
!!所有的结点都在e[]数组里 但是他们的排序不是按照e[]的下标按照顺序连续排序的 他们的排序是一个链表 存在ne[]数组里
注意 k结点的下一个结点的下标不一定是k+1 而是ne[k] 这就是k结点的下一个结点在e[]数组中的下标
而e[]数组中的元素的位置排序 是按照生成的时间来排序的 因为生成一个结点就是在e[]数组中新建一个数据
比如 第k个插入的点 他的下标是k-1 这里说的就是在e[]数组中的下标
例子




注意光标所在行给了特判
双链表(双向循环链表)
主要思想

在单链表的基础上 加了两个指针域函数 一个是l[ ] 一个是r[ ]

因为是双向循环链表 可以让0号位置的空间是 头结点
1号位置是尾结点
这样的话 head的值就是0 tail(指向尾结点的指针)的值就是1
操作
初始化+双向插入

初始化 因为是循环链表 头结点和尾结点也是双向链接 所以 r[0]=1 l[1]=0;
同时 因为0 1 的位置被占用了 所以idx初始化是2
插入:
在下标为k的节点后面插入
先新建结点 e[idx]=x
首先更新新节点的r 和 l
然后 更新两端结点的指针数组
先更新 右端点的 l[ ]数组 再更新左端点的 r[ ] 数组
不然如果先更新r 那么就找不到右端点的下标了 也就是找不到右端点了
在下标为k的点的左边插入

在k左边插入 实际上就是k的前一个结点的右边插入 所以改一下函数输入就行 add(l[k],x)
删除第k个点

将左边点的r 更新为 右边点的下标
将右边点的l 更新为 左边点的下标

邻接表
主要思想

就是将所有节点的邻节点用链表存了起来
栈和队列
栈
主要思想
先进后出
主要操作

tt是栈顶指针 也就是栈顶下标 初始值为0(主要目的是好判断是不是空 因为初始化为0之后 一旦有元素插入 那么tt>0)
队列
主要思想
先进先出
操作

hh表示队头下标 tt表示队尾下标
tt初始化为-1)(这里不用再向栈一样用tt>0来判断是不是为空了 直接用hh<=tt 来判断是不是有元素 所以tt就可以初始化为-1 这样插入元素的时候 直接从下标0开始)
hh初始化为0
(不进行初始化 默认是0)
单调栈与单调队列

单调栈
主要思想

单调栈的题型:
在i的位置插入一个数x
找到在该序列中 左边离x最近的且小于x的数
单调栈 主要就是将一个序列 找到他的性质 将其单调化 如下:

我们可以把i左边的数全部加入栈中
然后 对该栈进行一些处理 把那些相对位置在左边的且较大的数弹出 这样 整个栈就变成了一个单调递增的栈 与新插入进来的数进行比较的时候就比较方便 (进行该步时 先暂时不考虑是否相等的问题 因为现在先处理的是研究点x放入之前的状态)
当x插入之后 将x栈顶元素(stk[tt])与x比较 当栈顶元素比x大的时候 就出栈(tt–) 直到找到某个元素小于x 这样即可
例题



使用 cin.tie(0)
ios::sync_with_stdio(false)
可以使输入输出提高效率
单调队列
主要思想

从原序列中 找到一个性质 可以让序列变单调
例题



二级目录
二级目录
二级目录
二级目录
二级目录
一级目录
二级目录
二级目录
二级目录
相关文章:

算法--数据结构
这里写目录标题 本节内容链表与邻接表链表主要思想链表操作初始化在head结点后面插入普通插入删除操作 例子 双链表(双向循环链表)主要思想操作初始化双向插入删除第k个点 邻接表主要思想 栈和队列栈主要思想主要操作 队列主要思想操作 单调栈与单调队列…...
关系型数据库Redis安装与写入数据
文章目录 安装和初步选择数据库创建键值对数据类型 安装和初步 安装 Redis是开源的跨平台非关系型数据库,特点是占用资源低、查询速度快。 首先,在Github上下载最新发布的Redis-xxxx.zip压缩文件,下载之后解压,并将解压后的路径…...
《红蓝攻防对抗实战》十二.内网穿透之利用ICMP协议进行隧道穿透
内网穿透之利用ICMP协议进行隧道穿透 一.前言二.前文推荐三.利用ICMP协议进行隧道穿透1.ICMPsh获取反弹shell2.PingTunnel 搭建隧道 四.本篇总结 一.前言 本文介绍了利用ICMP协议进行隧道穿透的方法。ICMP协议不需要开放端口,可以将TCP/UDP数据封装到ICMP的Ping数据…...

【海德教育】国家开放大学和函授区别有:学校不同、入学门槛不同、学习方式不同、招生对象不同、学习年限不同,具体如下:
一、学校不同。 国家开放大学的招收学校是中央电大和各省市、自治州、市辖区及单设的国家开放大学。函授是成人高考学习方式,成考是普通高等院校举行的、单设的成人高等学校。 二、入学门槛不同。 国家开放大学对入学者的年龄、职业、地区和学习资历等方面都没有太多…...

单片机启动流程
存储器 一个单片机中存在rom和ram,Soc也有rom和ram(ddrx),部分Soc还包含MMU(Memory Manage Unit 内存管理单元)— (用于系统内存管理,比如说虚拟内存空间,内存区间的…...
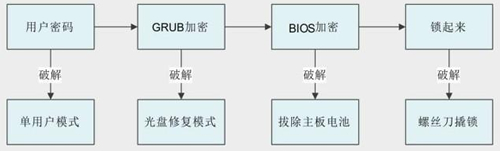
Linux学习教程(第二章 Linux系统安装)2
第二章 Linux系统安装 四、使用U盘安装Linux系统 前面章节介绍了如何通过虚拟机 VMware 安装 Linux 系统,而实际开发中,我们更多的是要将 Linux 系统直接安装到电脑上。 直接在电脑上安装 Linux 系统的常用方法有 2 种,分别是用光盘安装和用…...
操作系统 | proc文件系统
🌈个人主页:Sarapines Programmer🔥 系列专栏:《操作系统实验室》🔖少年有梦不应止于心动,更要付诸行动。 目录结构 1. 操作系统实验之proc文件系统 1.1 实验目的 1.2 实验内容 1.3 实验步骤 1.4 实验…...
)
刷题笔记(第五天)
1. 给定一个罗马数字,将其转换成整数。 罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。 字符 数值 I 1 V 5 X 10 L 50 C 100 …...

【OpenHarmony内核】Harmony内核互斥性信号量
文章目录 前言一、互斥性信号量是什么?二、互斥性信号量2.1 osSemaphoreNew函数创建并初始化一个信号量对象2.2 osSemaphoreGetName获取信号量对象的名称2.3 osSemaphoreAcquire获取一个信号量令牌2.4 osSemaphoreRelease2.5 osSemaphoreGetCount获取当前信号量令牌的数量2.6 …...

给OFFICE增加一个功能搜索
OFFICE功能几乎是无限的。不论你怎么熟悉,总有出乎意料的功能。前几天我使用EXCEL时,发现一个功能改名了。于是我就想,OFFICE应该增加一个功能搜索: 提供一个搜索输入栏。这个已经有了。输入搜索字串弹出一个面板,附带…...
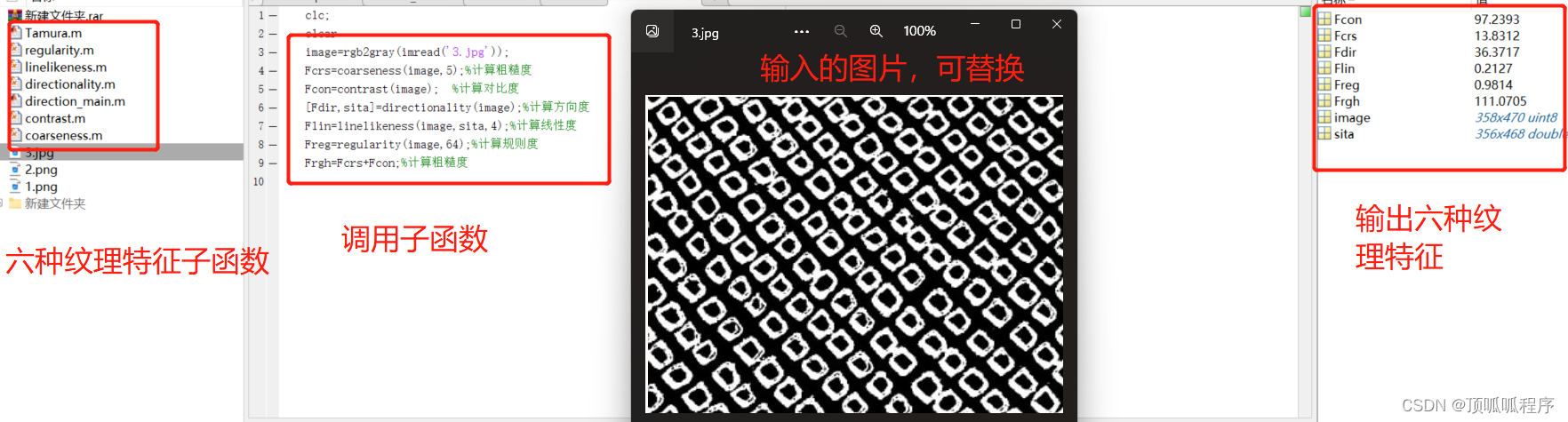
53基于matlab的Tamura纹理特征提取
基于matlab的Tamura纹理特征提取,包括粗糙度、对比度、方向度、线性度、规则度、粗糙度六种,可替换自己的数据进行特征提取。程序已调通,可直接运行。 53 方向度、线性度、规则度 (xiaohongshu.com)...

C++初阶--类与对象(3)(图解)
文章目录 再谈构造函数初始化列表隐式类型转换explicit关键字 static成员友元类内部类匿名对象拷贝函数时的一些优化 再谈构造函数 在我们之前的构造函数中,编译器会通过构造函数,对对象中各个成员给出一个适合的初始值,但这并不能称之为初始…...

考研分享第1期 | 末9生物跨专业考研北京大学电子信息404分经验分享
全文概览 一、个人信息 二、关于考研的经验分享 三、最后的小Tips 一、个人信息 姓名:Jackson 本科院校:某末流985生物专业 报考院校:北京大学电子信息专业 择校意向:北航计算机、人大高瓴、复旦软院、清华大学深研院、北…...

openGauss学习笔记-120 openGauss 数据库管理-设置密态等值查询-概述及使用gsql操作密态数据库
文章目录 openGauss学习笔记-120 openGauss 数据库管理-设置密态等值查询-概述及使用gsql操作密态数据库120.1 密态等值查询概述120.2 使用gsql操作密态数据库 openGauss学习笔记-120 openGauss 数据库管理-设置密态等值查询-概述及使用gsql操作密态数据库 120.1 密态等值查询…...
软件自动化测试平台
软件测试分类黑盒、白盒、功能、API、接口、压力测试和性能测试, 自动化测试平台是一种用于自动化执行软件测试过程的工具。 一、自动化测试平台-功能性 1. 接口自动化:对接软件的接口进行测试,验证接口的功能和性能。 2. Web 自动化&…...
)
springMVC 导出Excel ,并提供下载(处理日期格式问题)
目录 1、POI的三个依赖 2、控制层代码 3、业务层代码 4、参考文献: 1、POI的三个依赖 <!-- POI的三个依赖 --><dependency><groupId>org.apache.poi</groupId><artifactId>poi</artifactId><version>4.1.2</vers…...
 第二章软件过程 课后习题及其答案)
软件工程理论与实践 (吕云翔) 第二章软件过程 课后习题及其答案
软件工程理论与实践 (吕云翔) 第二章课后习题 第二章 软件过程 1.判断题 (1)瀑布模型的最大优点是将软件开发的各个阶段划分得十分清晰。 ( ) (2)螺旋模型是在瀑布模型和增量模型的基础上增加了风险分析活动。( ) …...
HTML跳转锚点
跳转锚点适用于本页面和其他页面的任意标签的跳转以及JavaScript的运行 使用方法即给标签加上独一无二的id属性,再使用a标签跳转 如果是其他页面的标签只需加上其他页面的路径,eg.href"其他页面的路径#zp1" id属性的最好不要使用数字开头 <…...

新能源汽车高压线束是如何快速连接到测试设备上进行电性能测试的
快速连接形成稳定的电测试在新能源行业里面是很常见的测试场景,比如说在新能源汽车行业的电池包、电机、电控制器的电性能测试中会有很多高压线束,需要将这些线束和电池包、电控制器、电机与测试设备快速连接在一起进行相关的EOL/DCR测试。 新能源汽车高…...
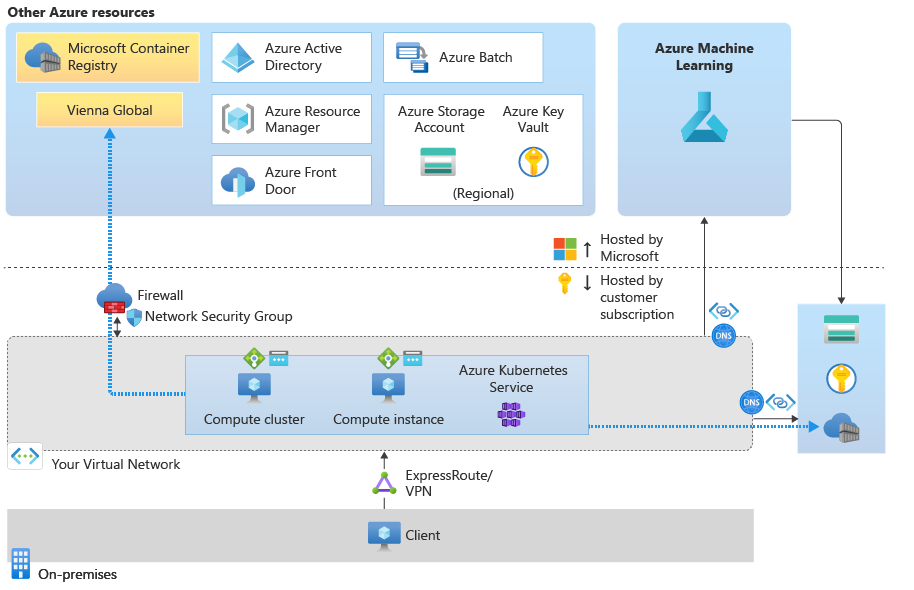
Azure 机器学习 - 使用受保护工作区时的网络流量流
目录 环境准备入站和出站要求方案:从工作室访问工作区方案:从工作室使用 AutoML、设计器、数据集和数据存储方案:使用计算实例和计算群集方案:使用联机终结点入站通信出站通信 方案:使用 Azure Kubernetes 服务方案&am…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
