数据结构之红黑树
红黑树的概念
红黑树(Red-Black Tree)同AVL树一样, 也是一种自平衡的二叉搜索树, 但在每个结点上增加一个存储位表示结点的颜色, 可以是Red或Black, 通过对任何一条从根到叶子的路径上各个结点着色方式的限制, 红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的. (最长路径也不会超出最短路径的两倍, 因此红黑树的平衡性要求相对宽松. 没有AVL树那样严格)

红黑树的性质(重要)
1. 每个结点不是红色就是黑色
2. 根结点是黑色的
3. 如果一个结点是红色的, 则它的两个孩子结点是黑色的(不能有连续的红色结点).
4. 对于每个结点, 从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点.
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点NIL).
为什么满足上面的性质, 红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
我们可以先来分析一种极端的情况,如果一颗红黑树有红有黑, 那它的最短路径一定是一条全黑的路径, 想要获取最长的路径, 就可以在此基础上继续添加红色结点, 因为只要红色结点不相邻, 添加红色结点能保证路径的黑色结点数不变, 那就可以创建一条一黑一红一黑一红..的路径, 这条路径就是最长的路径, 所以最长路径最多是最短路径的两倍, 不可能超过最短路径两倍, 最长的路径都超不过其它的路径更超不过.
另一个问题, 性质5中每个叶子结点都是黑色的(此处的叶子结点指的是空结点, 也被称为NIL节点), 有什么用?
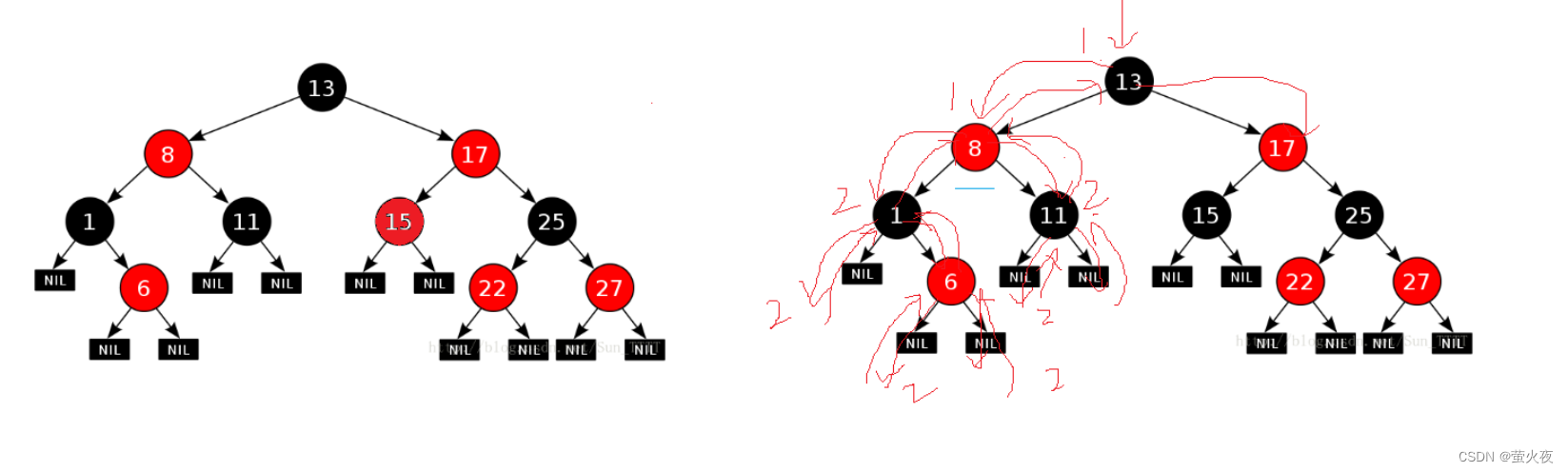
 这个红黑树有多少条路径?
这个红黑树有多少条路径?
如果不带空的话, 我们可能会认为有5条, 但是这里计算路径其实应该走到空(NIL),所以正确的应该是有11条路径, 我们可以认为这条规则就是为了更好的帮我们区分不同路径的。
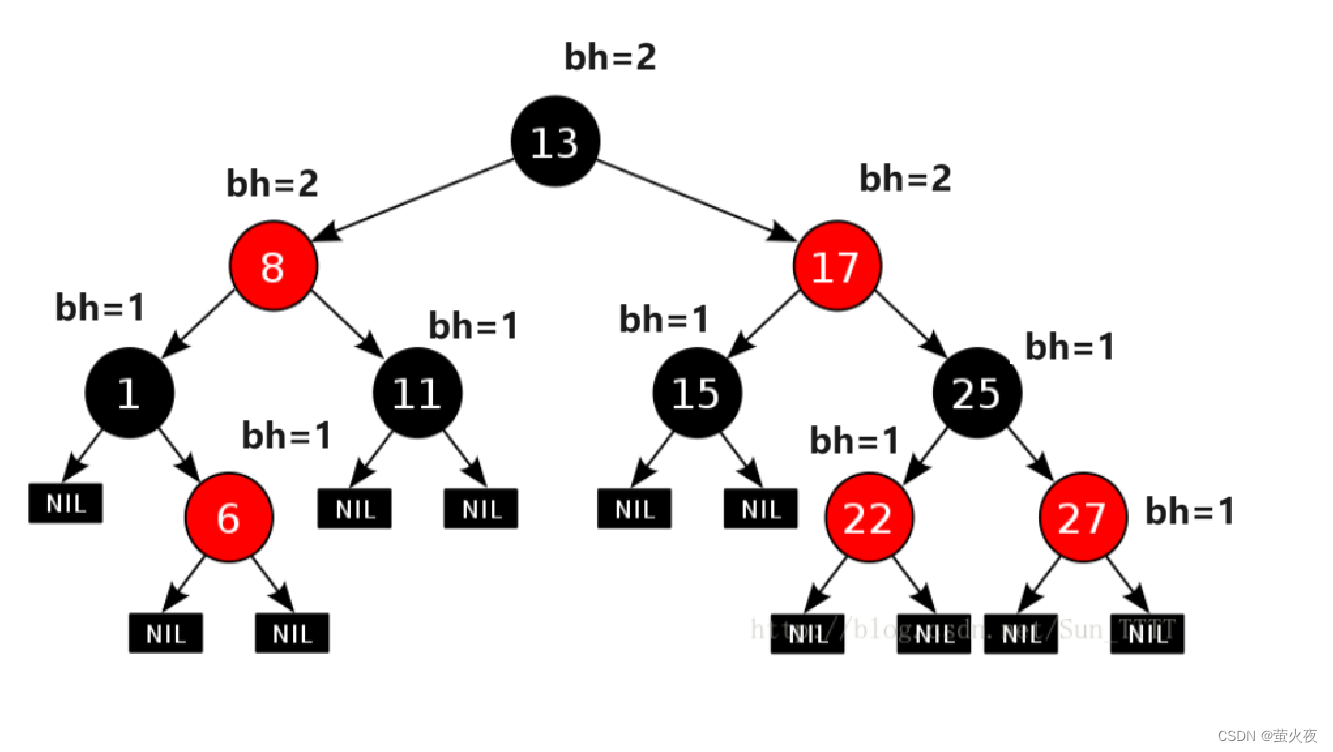
结点的黑高(黑色高度):从某结点出发(不含该结点)到达任一空叶结点的路径上经过的黑结点总数 .
有了AVL树, 为啥还要有红黑树?
对于一棵红黑树来说, 如果它里面全部的黑色结点一共有N个的话, 那它的最短路径长度就差不多是
, 然后整棵树的节点数量就是在N-2N之间
设红黑树的高度为h, 总结点数为n, 首先, 从任意节点出发, 到其子树的叶子节点的路径中黑色节点的数量称为该节点的黑高, 即bh, 设根节点为T,那么根节点的黑高就是bh(T), 假设一棵红黑树全部都是黑色节点, 那么它的黑高bh(T)就是它的树高,我们可得这样一棵树的结点数为(根据满二叉树的高度与节点数量的关系):, 我们还要考虑红色节点, 所以在此基础上加上红色节点的数量, 那么不论加几个红色节点, 只要增加, 一定满足下式:
根据红黑树的性质,我们可知根节点的黑高bh(T)至少为h/2 (h为树高),也就是说: , 所以
, 所以
.
AVL树
平衡标准比较严格:每个左右子树的高度差不超过1
最大高度是 1.44 ∗ log2 n + 2 − 1.328(100W个节点,AVL树最大树高28)
搜索、添加、删除都是 O(logn) 复杂度,其中添加仅需 O(1) 次旋转调整、删除最多需要 O(logn) 次旋转调整
红黑树
平衡标准比较宽松:没有一条路径会大于其他路径的2倍
最大高度是 2 ∗ log2(n + 1)( 100W个节点,红黑树最大树高40)
搜索、添加、删除都是 O(logn) 复杂度,其中添加、删除都仅需 O(1) 次旋转调整
如何选择
搜索的次数远远大于插入和删除,选择AVL树;搜索、插入、删除次数几乎差不多,选择红黑树
相对于AVL树来说,红黑树牺牲了部分平衡性以换取插入/删除操作时少量的旋转操作,整体来说性能要优于AVL树
红黑树的平均统计性能优于AVL树,实际应用中更多选择使用红黑树
红黑树结构的定义
先来定义一下红黑树的结构:
结点的颜色我们可以用一个枚举:
enum COLOR
{RED,BLACK
};结点的结构:
template<class T>
struct RBTreeNode
{RBTreeNode<T>* _parent;RBTreeNode<T>* _right;RBTreeNode<T>* _left;T _val;COLOR _col;RBTreeNode(const T& val): _parent(nullptr), _right(nullptr), _left(nullptr), _val(val), _col(RED){}};这里结点的颜色我们默认给的是红色, 为什么要选择红色, 黑色不可以吗?
如果我们插入一个新结点给的是黑色, 那它一定会违反上面提到的红黑树的性质——每条路径上黑色结点的数量一致:
因为原来每条路径黑色结点数量是相同的,现在新插入一个黑色结点的话, 那插入的这条路径会增加一个黑色结点, 但是其它路径数量不变, 所以其它所有的路径黑色结点数量都和这一条不相等, 这样再调整就比较麻烦了, 相当于影响了这棵树"全家"。
那如果我们插入结点默认给红色呢?
红色的话要看具体情况了:如果它的父亲是黑色, 那就没问题, 不需要进行什么处理:
如果插入一个红色结点, 但是它的父亲也是红色, 那就出事了, 因为红黑树里面不能出现连续的红色结点,那这种情况就需要调整了:
但是这样的调整的代价相对来说比较小, 因为可能不需要改动全局, 只是改变一个局部, 下面再具体说.
树的结构:
template<class T>
class RBTree
{
public://成员函数
private:RBTreeNode<T>* _root = nullptr;
};插入
由于红黑树也是一种二叉搜索树, 是在二叉搜索树的基础上加上其平衡限制条件来实现平衡,所以红黑树插入的逻辑也根搜索二叉树一样:
如果插入的是根结点, 根结点要手动设置为黑色.

bool Insert(const pair<K,V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col= BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);//cur->_col = RED; //默认cur就是红色if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent; //记得要链接父亲}else if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent; //记得要链接父亲}elseassert(false);//下面是调整//....
}根据颜色开始调整
对于红黑树来说, 插入新结点之后, 我们要检查红黑树的性质是否遭到破坏, 如果遭到破坏的话, 就需要进行相应的调整, 因为新节点的默认颜色是红色, 因此:
如果其双亲节点的颜色是黑色, 没有违反红黑树任何性质, 则不需要调整;
但当新插入节点的父亲节点是红色时, 就违反了性质不能有连续红色结点出现, 此时需要对红黑树的颜色进行调整:
约定: cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
而出现连续的红色结点的情况可以分为2种:
1. cur为红, p为红, g为黑, u存在且为红
2. cur为红, p为红, g为黑, u不存在或为黑
可以看到关键就在于叔叔结点, 为什么? 因为到这种情况了cur和parent此时一定是红色, grandfather结点一定是黑色, 唯一有区别的只是叔叔结点.
情况一: cur为红,p为红,g为黑,u存在且为红

解决方式:将p,u改为黑, g改为红, 然后把g当成cur, 继续向上调整。


可以看到叔叔为红的这种情况下只需要调整颜色就能又满足规则.
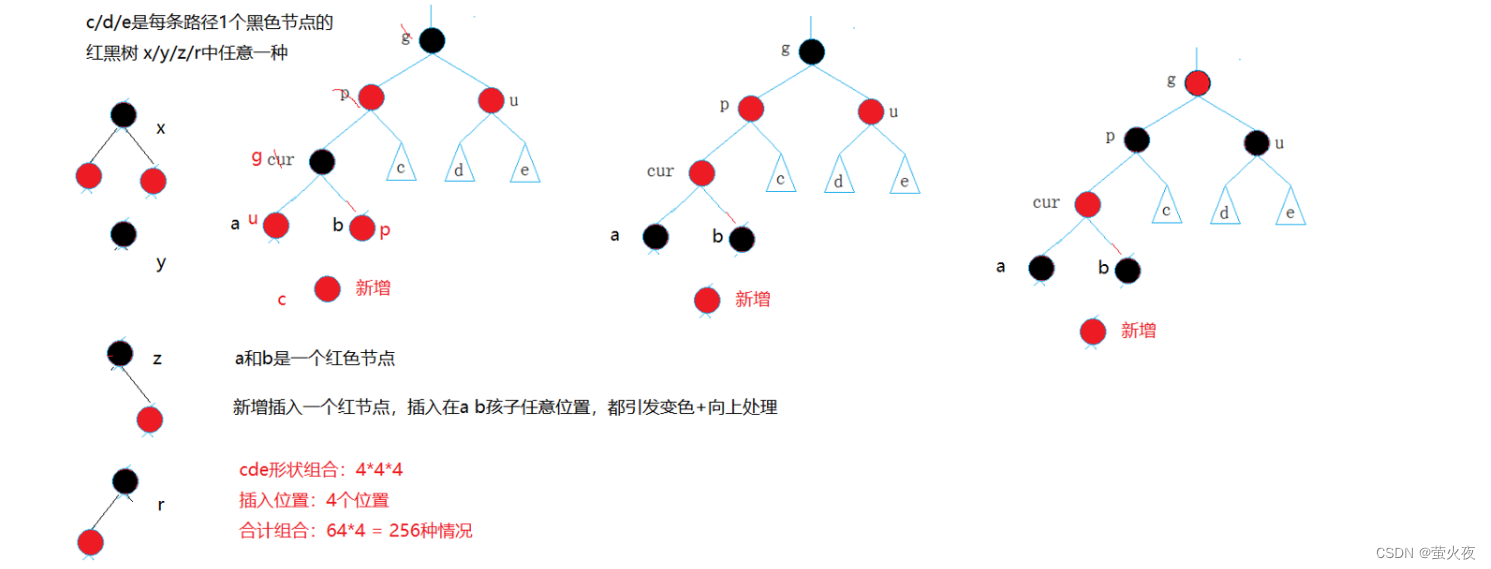
可以简单讨论一下子树路径黑结点和为1和2时候共有几种情况:
当a,b,c,d,e都是0的时候,有四种情况:

当a,b,c,d,e都是1的时候:
while (parent && parent->_col == RED)
{Node* grandparent = parent->_parent;//parent在grandparent的左if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}}//如果parent在grandparent的右,逻辑类似else if (parent == grandparent->_right){Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}}_root->_col = BLACK;//不管中间调了多少次,最后的根一定是黑,//如果被调整到根变红了,需要调为黑,如果没调到,重新赋值一遍也没有影响
}parent颜色为黑不需要单独去判断, 因为本来就不需要任何操作, 根本不会进入循环.
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑

说明: u的情况有两种
1.如果u节点不存在, 则cur一定是新插入节点, 因为此时c,a,b,d,e都是空, 因为要满足一个路径的黑色结点个数相同.
2.如果u节点存在, 则其一定是黑色的, 那么cur节点原来的颜色一定是黑色的, 上面看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改成红色。
在这里又可以再细分为两种子情况:
1. p为g的左孩子,cur为p的左孩子(左左)和p为g的右孩子, cur为p的右孩子(右右).
2. p为g的左孩子,cur为p的右孩子(左右)和p为g的右孩子, cur为p的左孩子(右左).
1.左左和右右
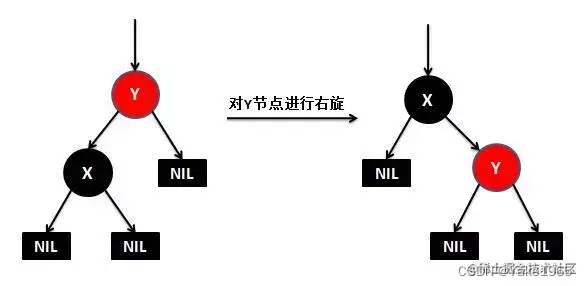
那对于这种情况我们要进行的单旋转+变色.
旋转:
为什么要旋转?
因为这种情况的话最长路径有可能已经超过最短路径的两倍了, 比如上面这个图如果如果d/e是空的话就已经超过了, 所以要先旋转降高度, 再去调整颜色使它符合红黑树.
进行什么旋转呢?
那就要看具体情况了, 其实还是我们AVL树那里的四种情况:
当前我们是 p为g的左孩子, cur为p的左孩子, 是在较高左子树的左侧插入(左左), 所以要进行的旋转是右单旋;
同理p为g的右孩子, cur为p的右孩子,是在较高右子树的右侧插入(右右),进行左单旋.
变色:
变色的话不论那种旋转是统一的:p、g变色–p变黑,g变红

为什么不直接把cur变黑呢?
这样也满足路径黑结点和保持不变啊:

此时parent的颜色又变成了红色, 又需要再继续向上调整, 而一开始的方法中parent调整完就是黑的, 就结束了, 不需要再向上调整, 更简便!
代码:
while (parent && parent->_col == RED)
{Node* grandparent = parent->_parent;//parent在grandparent的左if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_left){rotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}}}//parent在grandparent的左else if (parent == grandparent->_right){Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_right){rotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}}}_root->_col = BLACK;
}这里的旋转复用AVL的旋转即可, 去掉更新平衡因子的部分.
2.左右和右左
双旋+变色
前提条件根上面一样,还是cur为红,p为红,g为黑,u不存在/u存在且为黑
 ''
''
进行什么旋转呢?
1.p为g的左孩子,cur为p的右孩子,则针对p做左单旋, g作右单旋
2.相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋, g作左单旋.
以左右单旋图中为例, 先进行一个左单旋:

再进行一个右单旋:
 再变色:
再变色:

这样就调整好了
代码:
while (parent && parent->_col == RED)
{Node* grandparent = parent->_parent;//parent在grandparent的左if (parent == grandparent->_left){Node* uncle = grandparent->_right;//叔叔存在且为红直接变色if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}//叔叔不存在或者叔叔是黑进行旋转else{/右单旋if (cur == parent->_left){rotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}//左右双旋else if (cur == parent->_right){rotateL(parent);rotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}}//parent在grandparent的左else if (parent == grandparent->_right){//叔叔存在且为红直接变色Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}//叔叔不存在或者叔叔是黑进行旋转else{//左单旋if (cur == parent->_right){rotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}//右左双旋else if (cur == parent->_left){rotateR(parent);rotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}}_root->_col = BLACK;
}红黑树的测试
验证其为搜索二叉树
首先我们还是先来验证他是否是二叉搜索树,看它中序是否有序就行了:
void InOrderPrint()
{_InOrder(_root);
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);
}int main()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrderPrint();cout << endl;return 0;
}
顺序是正确的
验证其是否平衡且满足红黑树性质
如何判断它是否满足是一棵红黑树呢?
其实就是去检查那几条规则(性质):
1.首先结点颜色要么是黑色, 要么是红色, 这没什么好检查的。
2.然后根结点必须是黑色, 这个可以检查一下,如果根结点不是黑色(是红色)直接就不符合了
3.然后如果出现连续的红色结点, 那也不符合。
那怎么检查有没有出现连续红色结点呢?
我们可以去遍历这棵树, 然后遇到红色结点判断它的孩子是不是红色结点, 如果存在红色结点它的孩子也是红色, 那就不符合, 这样可以,但是不太好, 因为孩子的话要检查两个,而且结点的孩子有还有可能不存在, 为空, 那还得再加一个判断。
所以我们可以这样做: 遍历遇到红色结点我们去看它的父亲, 如果它的父亲也为红色那就不行。而判断父亲的话, 只有根结点没有父亲, 但是根结点是黑色的也不会去检查它。
bool IsBalance()
{if (_root == nullptr)return true;if (_root->_col == RED)return false;return _Check(_root);
}bool _Check(Node* root)
{if (root == nullptr){return true;}if (root->_col == RED && root->_parent->_col == RED)return false;return _Check(root->_left, blacknum, ref)&& _Check(root->_right, blacknum, ref);
}然后还剩一个, 我们要检查每条路径黑色结点数量是否相等, 存在不相等的情况就不符合。
那这个要如何检查呢?
我们可以先求出一条路径的黑色结点数量, 把它作为基准值, 然后再递归求出每条路径的黑色结点数量和它比较, 如果存在不相等的情况, 就不符合, 不用管这个基准值是不是正确的, 只要其他路径和这个值不相同, 那就不符合.
bool IsBalance()
{if (_root == nullptr)return true;if (_root->_col == RED)return false;//找基准值,这里以最左路为基准Node* cur = _root;int ref = 0;while (cur){if (cur->_col == BLACK){ref++;}cur = cur->_left;}//定义一个blacknum来记录路径的黑色结点数目int blacknum = 0;return _Check(_root, blacknum,ref);
}bool _Check(Node* root,int blacknum, const int ref)
{if (root == nullptr){//root为空说明该路径已经找完,开始比较blacknum和ref,不相等就不符合if (blacknum != ref)return false;return true;}//如果节点是黑的blacknum就++if (root->_col == BLACK)blacknum++;//结点是红色判断它与父亲结点是否为连续的红if (root->_col == RED && root->_parent->_col == RED)return false;//继续判断左右子树return _Check(root->_left, blacknum, ref)&& _Check(root->_right, blacknum, ref);
}注意这里的blacknum传递的非常巧妙, 因为每一层的blacknum都是独立的, 所以向下一层传递blacknum的后blacknum的修改不会影响上一层, 为什么不想去影响上一层呢? 因为上一层的blacknum传递给了左子树后还要传递给右子树进行判断, 在左子树中修改了上一层的值那再传给右子树就一定错了.
大量随机数构建红黑树进行测试
int main()
{const int N = 10000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << "Insert_time:" << end2 - begin2 << endl;cout << t.IsBalance() << endl;return 0;
} 
插入和查找的时间测试:
Node* Find(const pair<K, V>& kv)
{Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){cur = cur->_right;}else if (kv.first < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;
}int main()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();size_t begin1 = clock();for (auto e : v){t.Find(make_pair(e,e));}size_t end1 = clock();cout << "Find_time:" << end1 - begin1 << endl;cout << "Insert_time:" << end2 - begin2 << endl;cout << "是否平衡:"<<t.IsBalance() << endl;return 0;
}
插入相同数量随机数比较AVL树和红黑树的高度
void test3()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand()+i);}RBTree<int, int> rbt;AVLTree<int, int> avlt;for (auto e : v){rbt.Insert(make_pair(e, e));avlt.Insert(make_pair(e, e));}cout << "插入了" << rbt.Size() << "个值" << endl;cout << "红黑树高度: " << rbt.Height()<<endl;cout << "AVL树高度: " << avlt.Height() << endl;}当N为10w:

插入10万个数据, 对产生的随机数都加个i(减少重复值), 我们看到就有一些差异了
当N为100w:

100w个数据的差异就更大了, 还是红黑树要高一点
可以发现AVL树对平衡的控制是比较严格的, 而红黑树是相对宽松的。
红黑树的删除
简单分析:
删除节点一定都在最后一到两层, 因为上层都可以替代下去.
结点有红色节点和黑色节点, 我们就以删除节点的颜色来区分删除操作的所有情况
删除红色节点
如果删除的节点是红色直接删除, 不用作任何调整。因为删除最后一层的红色节点, 并没有影响红黑树的任何性质。
删除黑色节点
有3种情况:
1. 拥有 2 个红色子节点的黑色节点
不可能被直接删除,因为会找它的子节点替代删除,因此不用考虑这种情况
2. 拥有 1 个红色子节点的黑色节点
修复步骤总结:
- 用删除节点的唯一子节点对其进行替代
- 将替代节点染成黑色
3. 黑色叶子节点
1. 删除节点为根节点, 直接删除该节点, 无需做其他操作。
2. 删除节点的兄弟节点为黑色
2.1兄弟节点至少有1个红色子节点
2.1.1 兄弟节点有一个右子节点:
2.1.2 兄弟节点有一个左子节点:
2.1.3 兄弟节点有两个左右子节点:
修复步骤总结:
1 进行旋转操作
2 旋转之后的中心节点继承父节点(删除节点的父节点)的颜色
3 旋转之后的左右节点染为黑色
2.2 兄弟节点没有红色子节点
2.2.1父节点为红色
2.2.2父节点为黑色
修复步骤总结:
- 父节点向下与兄弟节点进行合并
- 将兄弟染成红色、父节点染成黑色即可修复红黑树性质
- 如果父节点是黑色,直接将父节点当成被删除的节点处理,来修复父节点的下溢情况
3. 删除节点的兄弟节点为红色
修复步骤总结:
- 兄弟节点染成 BLACK, 父节点染成染成 RED, 对父节点进行右旋
- 于是又回到兄弟节点是黑色的情况(侄子节点变为兄弟节点),继续使用兄弟节点为黑色的方法进行修复
具体可查看:
【精选】【数据结构】史上最好理解的红黑树讲解,让你彻底搞懂红黑树_小七mod的博客-CSDN博客
完整代码:
#pragma once
#include<assert.h>
enum COLOR
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K,V>* _parent;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _left;pair<K,V> _kv;COLOR _col;RBTreeNode(const pair<K,V>& kv): _parent(nullptr), _right(nullptr), _left(nullptr), _kv(kv), _col(RED){}};template<class K,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public:bool Insert(const pair<K,V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col= BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);//cur->_col = RED;if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}elseassert(false);//插入完成, 调整颜色parent的颜色是黑,不需要调整//if (parent->_col == BLACK)//{// return true;//}//parent的颜色是红,需要调整while (parent && parent->_col == RED){Node* grandparent = parent->_parent;//parent在grandparent的左// g g// p u p u//c cif (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{// g// p u//cif (cur == parent->_left){rotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}// g// p u// celse if (cur == parent->_right){rotateL(parent);rotateR(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}}//parent在grandparent的左// g g// u p u p// c celse if (parent == grandparent->_right){Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{// g// u p// cif (cur == parent->_right){rotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}// g// u p// celse if (cur == parent->_left){rotateR(parent);rotateL(grandparent);grandparent->_col = RED;cur->_col = BLACK;}}}_root->_col = BLACK;}return true;}void InOrderPrint(){_InOrder(_root);}bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;Node* cur = _root;int ref = 0;while (cur){if (cur->_col == BLACK){ref++;}cur = cur->_left;}int blacknum = 0;return _Check(_root, blacknum,ref);}Node* Find(const pair<K, V>& kv){Node* cur = _root;while (cur){if (kv.first > cur->_kv.first){cur = cur->_right;}else if (kv.first < cur->_kv.first){cur = cur->_left;}else{return cur;}}return nullptr;}int Height(){return _Height(_root);}private:Node* _root = nullptr;bool _Check(Node* root,int blacknum, const int ref){if (root == nullptr){if (blacknum != ref)return false;return true;}if (root->_col == BLACK)blacknum++;if (root->_col == RED && root->_parent->_col == RED)return false;return _Check(root->_left, blacknum, ref)&& _Check(root->_right, blacknum, ref);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}int _Height(Node* root){if (root == nullptr)return 0;int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void rotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_right)parentParent->_right = subR;else if (parent == parentParent->_left)parentParent->_left = subR;subR->_parent = parentParent;}}void rotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;subL->_right = parent;parent->_left = subLR;parent->_parent = subL;if (subLR)subLR->_parent = parent;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else if (parentParent->_right == parent){parentParent->_right = subL;}subL->_parent = parentParent;}}
};test.cpp:
#include <iostream>
#include <vector>
using namespace std;
#include "RBTree.h"
#include "AVL.h"void test1()
{//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.InOrderPrint();cout << endl;cout << t.IsBalance() << endl;
}void test2()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}size_t begin2 = clock();RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();size_t begin1 = clock();for (auto e : v){t.Find(make_pair(e, e));}size_t end1 = clock();cout << "Find_time:" << end1 - begin1 << endl;cout << "Insert_time:" << end2 - begin2 << endl;cout << "是否平衡:" << t.IsBalance() << endl;
}void test3()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand()+i);}RBTree<int, int> rbt;AVLTree<int, int> avlt;for (auto e : v){rbt.Insert(make_pair(e, e));avlt.Insert(make_pair(e, e));}cout << "红黑树高度: " << rbt.Height()<<endl;cout << "AVL树高度: " << avlt.Height() << endl;}
int main()
{test3();return 0;
}
相关文章:

数据结构之红黑树
红黑树的概念 红黑树(Red-Black Tree)同AVL树一样, 也是一种自平衡的二叉搜索树, 但在每个结点上增加一个存储位表示结点的颜色, 可以是Red或Black, 通过对任何一条从根到叶子的路径上各个结点着色方式的限制, 红黑树确保没有一条路径会比其他路径长出俩…...
【chat】4: ubuntu20.04:数据库创建:mysql8 导入5.7表
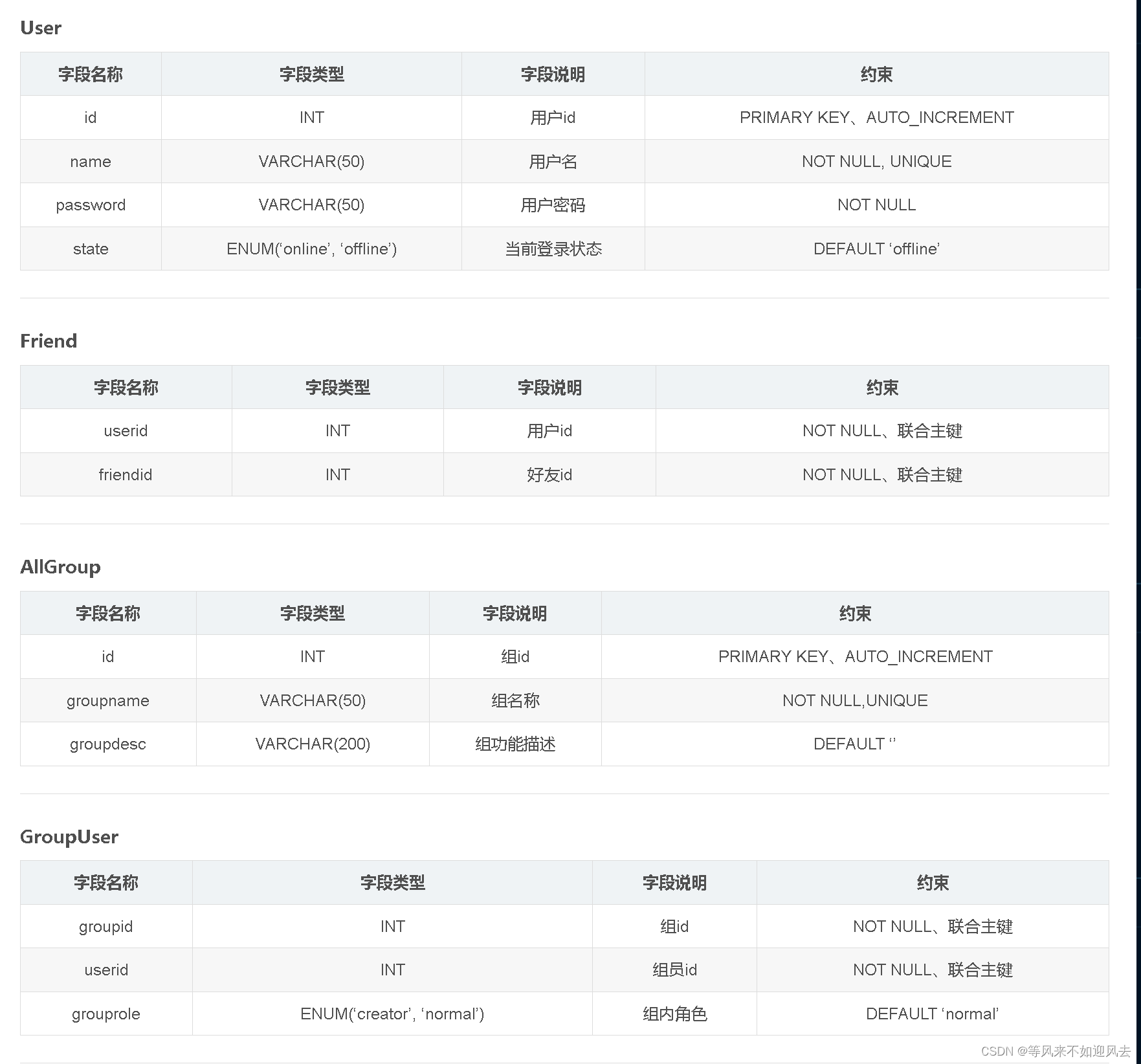
【chat】3: ubutnu 安装mysql-8 并支持远程访问 已经支持 8.0的SQLyog 远程访问:大神2021年的文章:sql是5.7的版本,我使用的ubuntu20.04,8.0版本:chat数据库设计 C++搭建集群聊天室(七):MySQL数据库配置 及项目工程目录配置 User表,以id 唯一标识 Friend 表,自己的id…...
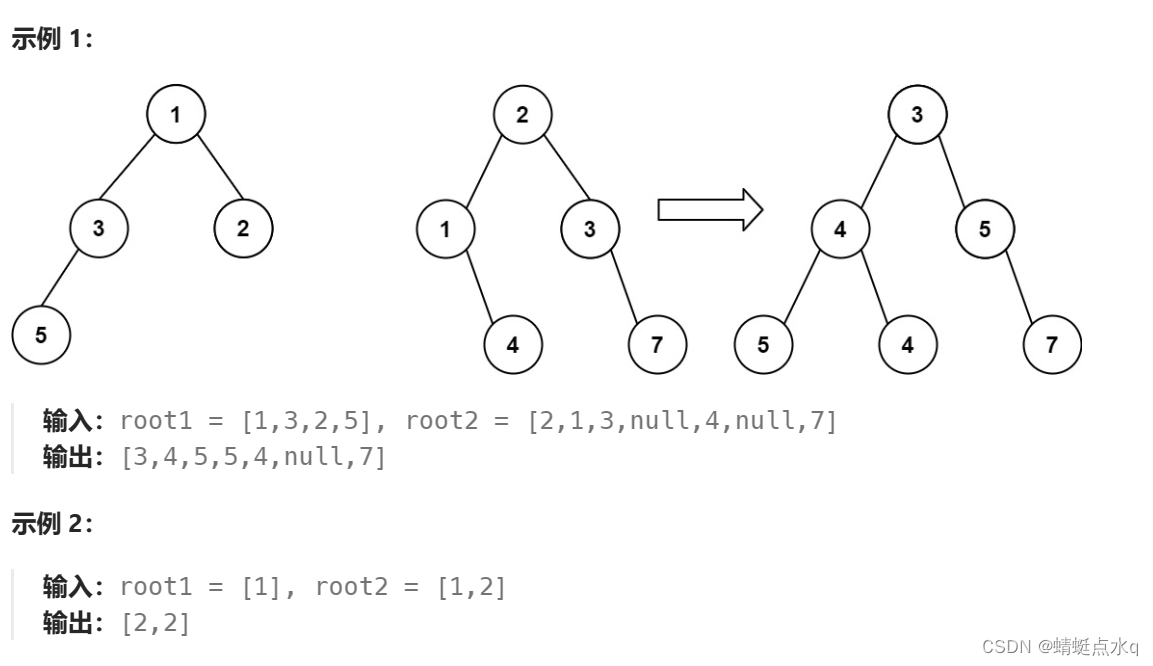
合并二叉树(Java)
题目描述 给你两棵二叉树: root1 和 root2 。 想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重…...

C语言 exit函数
c语言exit函数的详解_笔记大全_设计学院 (python100.com) “需要注意的是,在程序中使用exit函数会立即强制结束程序,程序内部未处理的任何资源都将不能释放,也就可能导致内存泄漏。因此,在使用exit函数之前,需要先释放…...

基于VPLC711的曲面外观检测XYR运动控制解决方案
市场应用背景 随着消费升级,产品形态正在朝着多样性和精细化方向迅速发展。这导致了对于复杂曲面轨迹加工的需求,包括外观检测、打磨抛光和点胶工艺控制,要求更高的精密度。企业必须主动满足市场需求,不断改进工艺,以…...

【LeetCode刷题-二分查找】--162.寻找峰值
162.寻找峰值 方法一:寻找最大值 题目保证了nums[i]≠nums[i1],所以数组nums中最大值两侧的元素一定严格小于最大值本身,因此最大值所在的位置就是一个可行的峰值位置 class Solution {public int findPeakElement(int[] nums) {int idx 0…...
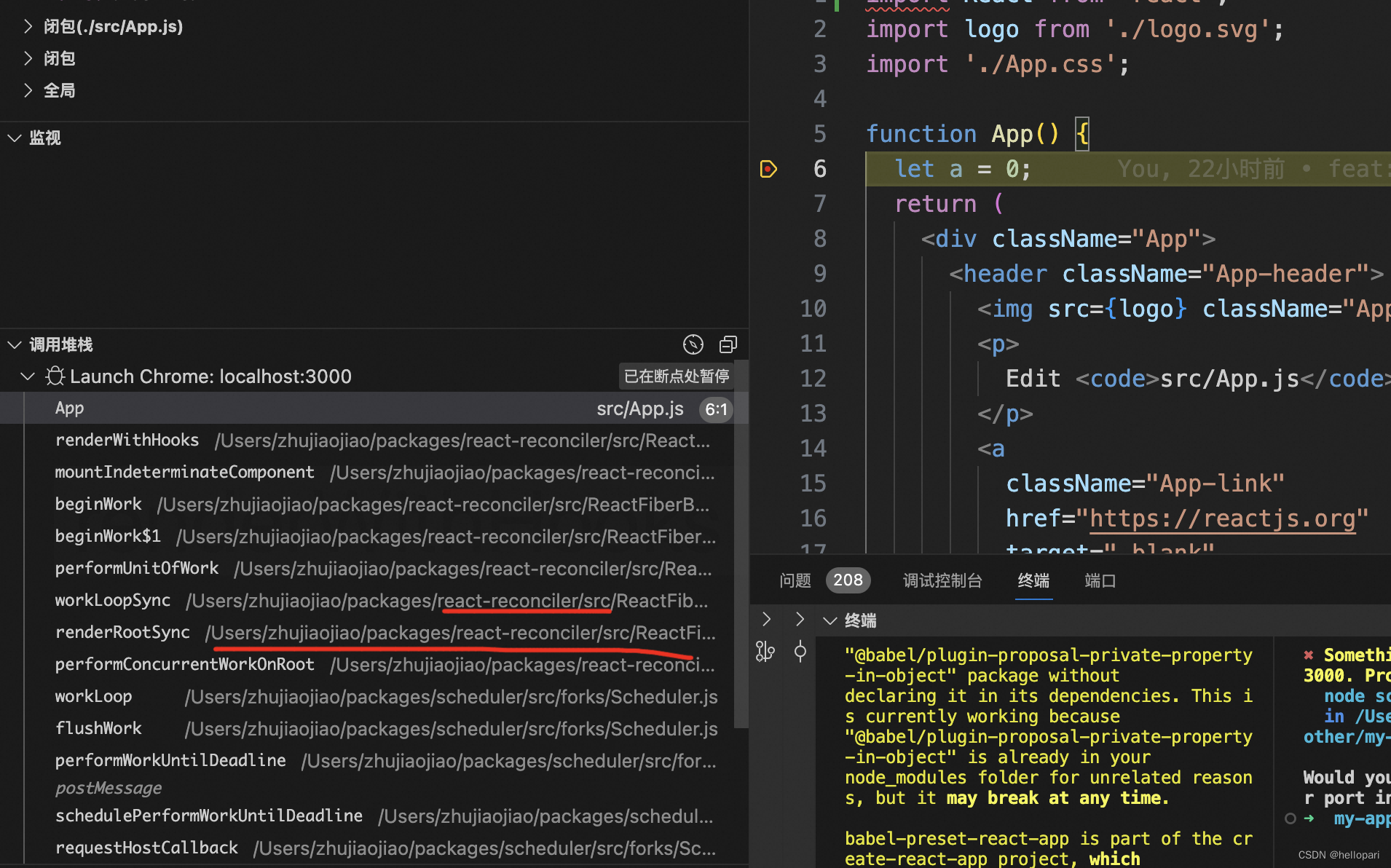
vscode调试react 最初的源码
如果直接在react项目中打点调试, 调试的是 react-dom.development.js, 而源码里这些逻辑是分散在不同的包里的,如何才能够调试 React 最初的源码呢? JS 代码经过编译,会产生目标代码,但同时也会产生 sourcemap。sourcemap 的作用就是映射目…...

Netty网络通信模型
传统IO模型: 传统IO模型就是阻塞IO,即处理业务逻辑的线程去进行IO,当然IO操作很耗时,然后线程就得阻塞,当然CPU会回收该线程的时间片,把该线程挂起,切换到其他线程去执行,在并发量大…...
.NET快速对接极光消息推送
什么是消息推送? 很多手机APP会不定时的给用户推送消息,例如一些新闻APP会给用户推送用户可能感兴趣的新闻,或者APP有更新了,会给用户推送是否选择更新的消息等等,这就是所谓的“消息推送”。 常见的一些APP消息推送…...
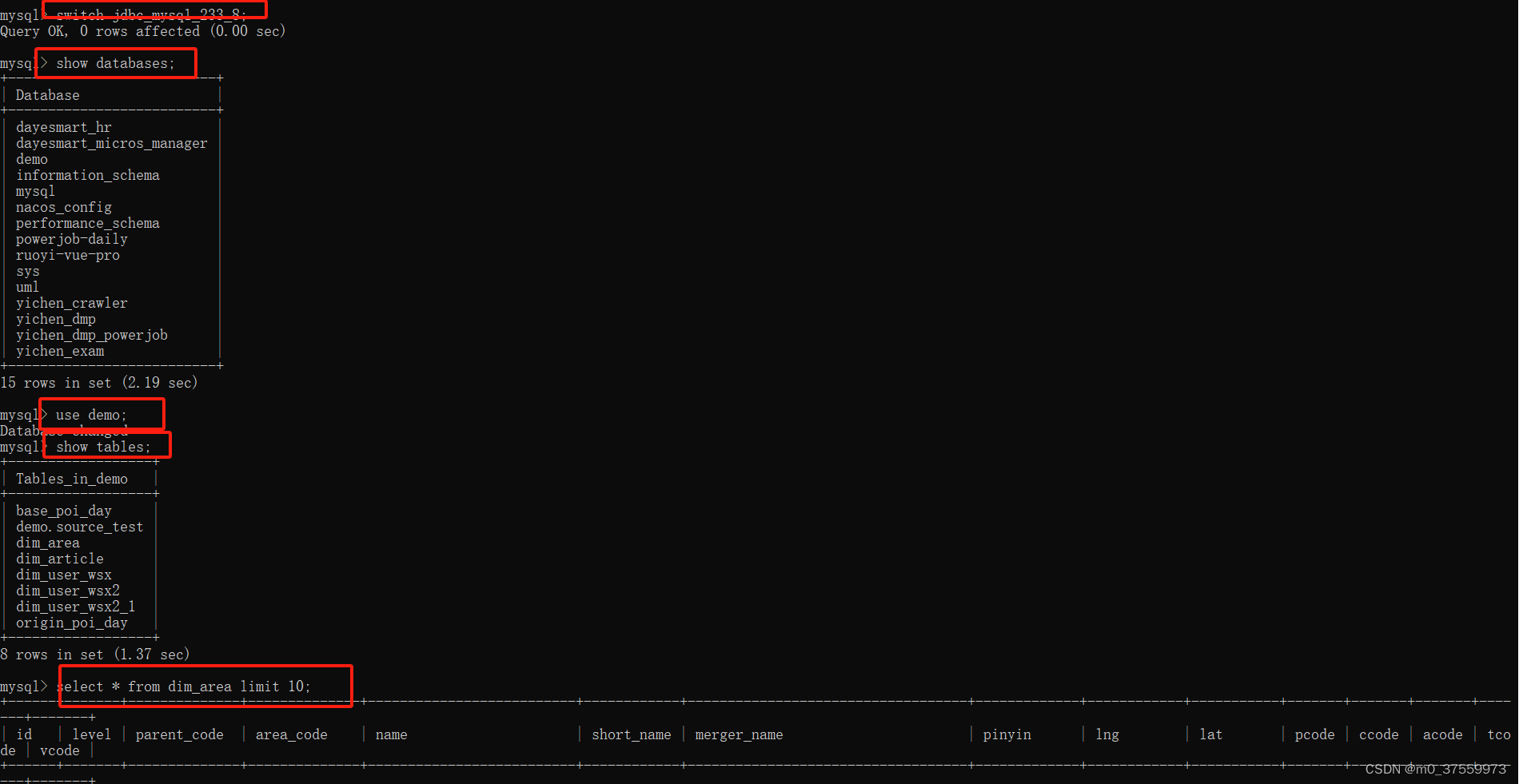
Doris:多源数据目录(Multi-Catalog)
目录 1.基本概念 2.基本操作 2.1 查看 Catalog 2.2 新增 Catalog 2.3 切换 Catalog 2.4 删除 Catalog 3.元数据更新 3.1手动刷新 3.2定时刷新 3.3自动刷新 4.JDBC Catalog 4.1 上传mysql驱动包 4.2 创建mysql catalog 4.3. 读取mysql数据 1.基本概念 …...

建行驻江门市分行纪检组以政治谈话压责任促发展
开展政治谈话,是加强“一把手”和领导班子监督、严肃党内政治生活、加强对党员领导干部日常教育管理的有效手段。 为督促“一把手”和领导班子成员依法依规履行职责、行使权力,推动党中央重大决策部署以及建设银行总行、广东省分行党委的决策部署在本单…...
如何从存档服务器上完全删除PDM用户
当创建新用户时使用“PDM 登录”类型(如下图),PDM用户名和密码会存储于存档服务器的注册表中。 存档服务器的注册表位置如下: HKEY_LOCAL_MACHINE\SOFTWARE\SolidWorks\Applications\PDMWorks Enterprise\ArchiveServer\ConisioU…...

导师对学生学术论文的指导包括哪些方面,请详细展开说明
导师在指导学生学术论文时涉及多个方面,这些方面旨在帮助学生培养独立研究和学术写作的能力。以下是一些导师可能涉及的主要方面: 1.选题和课题确定: 导师会与学生讨论潜在的研究兴趣和方向,帮助学生选择一个既有研究价值又符合其…...

嵌入式软件开发是个啥职业?
在硬件行业中,有一类工作岗位是更偏向软件的,或者说是软硬结合非常紧密的工作,那就是嵌入式开发工程师。 说起嵌入式,可能很多没有接触过电子类的人没有听说这些东西。 其实简单来说,嵌入式开发就是写程序去控制硬件电…...
03【远程协作开发、TortoiseGit、IDEA绑定Git插件的使用】
上一篇:02【Git分支的使用、Git回退、还原】 下一篇:【已完结】 目录:【Git系列教程-目录大纲】 文章目录 一、远程协作开发1.1 远程仓库简介1.1.1 Github1.1.2 Gitee1.1.3 其他托管平台 1.2 发布远程仓库1.2.1 创建项目1) 新…...

Linux:centos7通过yum安装mysql的方法
1. 检查mysql是否安装 yum list installed | grep mysql如果有的话,就全部卸载 yum -y remove 数据库名称2. MySQL依赖libaio,所以先要安装libaio yum search libaio # 检索相关信息 yum install libaio # 安装依赖包3. 下载MySQL Yum Repository 如…...
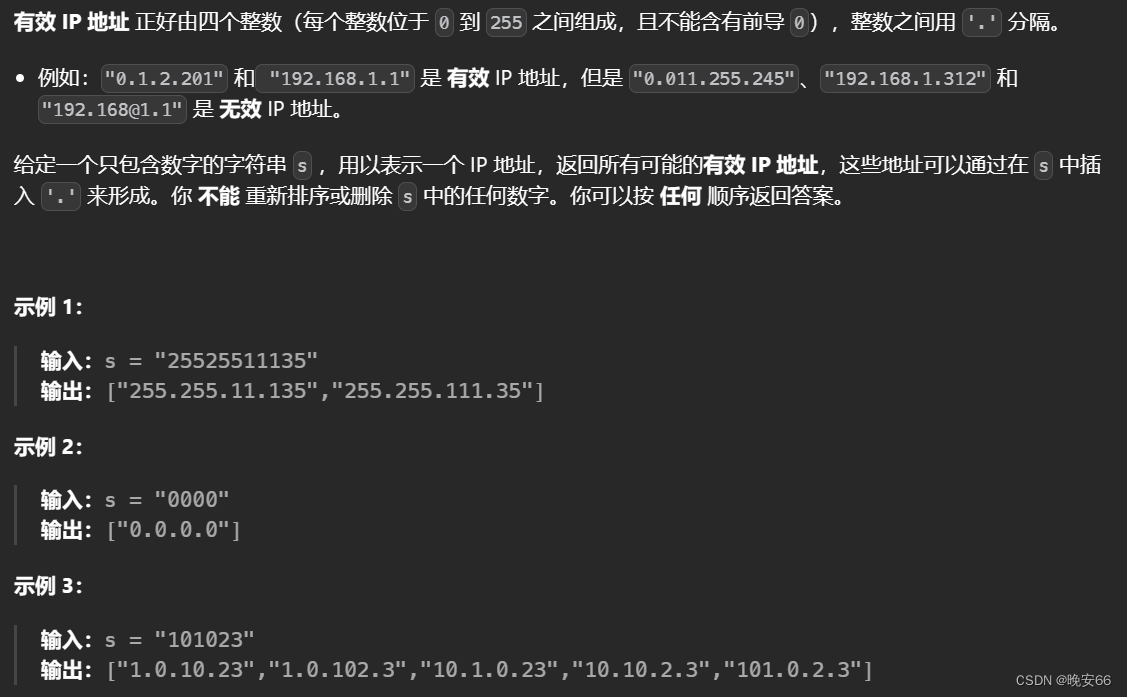
【算法与数据结构】93、LeetCode复原 IP 地址
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:参照【算法与数据结构】131、LeetCode分割回文串的思路,需要将IP字符串进行分割࿰…...
uniapp点击图片放大预览
阐述 有些时候我们在用uniapp显示图片时,有的不宜全部显示到屏幕上,uniapp提供了一个非常好用的api。 实现方式如下: <template><view class"content"><image class"logo" src"/static/images/a.…...
Java TreeMap
TreeMap 是一个基于 key 有序的 key value 散列表。 map 根据其键的自然顺序排序,或者根据 map 创建时提供的 Comparator 排序不是线程安全的key 不可以存入null底层是基于红黑树实现的 TreeMap 的类结构图: 实现了 NavigableMap 接口,Na…...

ubuntu 内网源如何搭建 —— 筑梦之路
为什么要搭建内网源? 原因:内网开发环境由于其特定原因不能上外网,所以需要本地环境下的内网源来方便开发人员下载安装软件 搭建建议 单独使用一块磁盘来存放源文件或者单独一个目录下,避免混淆。 环境说明 ubuntu 系统 两张…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...