[100天算法】-不同路径 III(day 73)
题目描述
在二维网格 grid 上,有 4 种类型的方格:1 表示起始方格。且只有一个起始方格。
2 表示结束方格,且只有一个结束方格。
0 表示我们可以走过的空方格。
-1 表示我们无法跨越的障碍。
返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。示例 1:输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出:2
解释:我们有以下两条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出:4
解释:我们有以下四条路径:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:输入:[[0,1],[2,0]]
输出:0
解释:
没有一条路能完全穿过每一个空的方格一次。
请注意,起始和结束方格可以位于网格中的任意位置。提示:1 <= grid.length * grid[0].length <= 20
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/unique-paths-iii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
从起始格子开始,尝试每一个 0 空格。当走到 2 时,如果此时网格没有还没走过的空格,说明这是一条可行的路径。也就是说我们需要用一个方式来标志已经走过的空格,可以把格子设为 -1,回溯时需要把格子重新设置为 0,不影响其他路径的尝试。
当我们走到 2 时,如何判断网格中是否还有未走过的空格?
每次都去遍历整个网格的话,时间复杂度太高。我们可以在开始先统计网格中一共有多少个可以走的格子,每走过一个格子计数器就减一。
复杂度
- 时间复杂度:$O(4^{mn})$, m, n 分别是网格的长宽。找到起始格子和统计空格用了 $O(mn)$,递归的时间复杂度 $O(4^{mn})$,网格一共有 $mn$ 个格子,每个格子有 4 个方向可以走。
- 空间复杂度:递归栈的最大空间 O(m∗n)。
p.s. 下方代码是我看错题了,求了所有路径。实际上只需要一个计数器来记录路径数,不消耗额外空间。
代码
JavaScript Code
/*** @param {number[][]} grid* @return {number}*/
var uniquePathsIII = function (grid) {const offsets = [[-1, 0],[1, 0],[0, -1],[0, 1],];const ans = [];const dfs = (grid, x, y, spaceCnt, path) => {if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length) return;if (grid[x][y] === 2) {spaceCnt === 0 && ans.push([...path]);return;}if (grid[x][y] === -1) return;grid[x][y] = -1; // mark// recursionfor (const [ox, oy] of offsets) {// p.s. 如果 (x+ox, y+oy) 不在网格中或者是障碍的话,也可以提前剪枝。dfs(grid, x + ox, y + oy, spaceCnt - 1, [...path, [x, y]]);}grid[x][y] = 0; // backtrack};let startPos = {};const init = grid => {let spaceCnt = 1; // 起始方格也是要走的一个格子for (let x = 0; x < grid.length; x++) {for (let y = 0; y < grid[x].length; y++) {if (grid[x][y] === 1) startPos = { x, y };if (grid[x][y] === 0) spaceCnt++;}}return spaceCnt;};// 统计要走的格子总数const spaceCnt = init(grid);dfs(grid, startPos.x, startPos.y, spaceCnt, []);return ans.length;
};相关文章:
)
[100天算法】-不同路径 III(day 73)
题目描述 在二维网格 grid 上,有 4 种类型的方格:1 表示起始方格。且只有一个起始方格。 2 表示结束方格,且只有一个结束方格。 0 表示我们可以走过的空方格。 -1 表示我们无法跨越的障碍。 返回在四个方向(上、下、左、右&#…...
【c++随笔12】继承
【c随笔12】继承 一、继承1、继承的概念2、3种继承方式3、父类和子类对象赋值转换4、继承中的作用域——隐藏5、继承与友元6、继承与静态成员 二、继承和子类默认成员函数1、子类构造函数 二、子类拷贝构造函数3、子类的赋值重载4、子类析构函数 三、单继承、多继承、菱形继承1…...
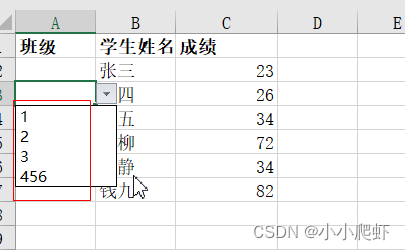
Excel中使用数据验证、OFFSET实现自动更新式下拉选项
在excel工作簿中,有两个Sheet工作表。 Sheet1: Sheet2(数据源表): 要实现Sheet1中的“班级”内容,从数据源Sheet2中获取并形成下拉选项,且Sheet2中“班级”内容更新后,Sheet1中“班…...

Android修行手册 - 可变参数中星号什么作用(冷知识)
点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&…...
视图缩放)
Python与ArcGIS系列(三)视图缩放
目录 0 简述1 在所有图层中缩放至所选要素2 在单独图层中缩放至所选要素3 改变地图范围0 简述 本篇介绍如何利用arcpy实现缩放视图到所选要素以及改变地图范围功能。 对于以及创建的选择集数据,通常需要进行缩放以更好地显示所选要素,要素缩放可分为两种:第一种是在所有图层…...
[ASP]数据库编辑与管理V1.0
本地测试:需要运行 ASP专业调试工具(自己搜索下载) 默认登陆口令:admin 修改口令:打开index.asp找到第3行把admin"admin"改成其他,如admin"abc123" 程序功能齐全,代码精简…...

MyBatis Plus整合Redis实现分布式二级缓存
MyBatis缓存描述 MyBatis提供了两种级别的缓存, 分别时一级缓存和二级缓存。一级缓存是SqlSession级别的缓存,只在SqlSession对象内部存储缓存数据,如果SqlSession对象不一样就无法命中缓存,二级缓存是mapper级别的缓存ÿ…...

如何帮助 3D CAD 设计师实现远程办公
当 3D CAD 设计师需要远程办公时,他们可能需要更强的远程软件,以满足他们的专业需求。比如高清画质,以及支持设备重定向、多显示器支持等功能。3D CAD 设计师如何实现远程办公?接下来我们跟随 Platinum Tank Group 的故事来了解一…...

如何在 Idea 中修改文件的字符集(如:UTF-8)
以 IntelliJ IDEA 2023.2 (Ultimate Edition) 为例,如下: 点击左上角【IntelliJ IDEA】->【Settings…】,如下图: 从弹出页面的左侧导航中找到【Editor】->【File Encodings】,并将 Global Encoding、Project E…...

【C++】单例模式【两种实现方式】
目录 一、了解单例模式前的基础题 1、设计一个类,不能被拷贝 2、设计一个类,只能在堆上创建对象 3、设计一个类,只能在栈上创建对象 4、设计一个类,不能被继承 二、单例模式 1、单例模式的概念 2、单例模式的两种实现方式 …...

php的api接口token简单实现
<?php // 生成 Token function generateToken() {$token bin2hex(random_bytes(16)); // 使用随机字节生成 tokenreturn $token; } // 存储 Token(这里使用一个全局变量来模拟存储) $tokens []; // 验证 Token function validateToken($token) {gl…...
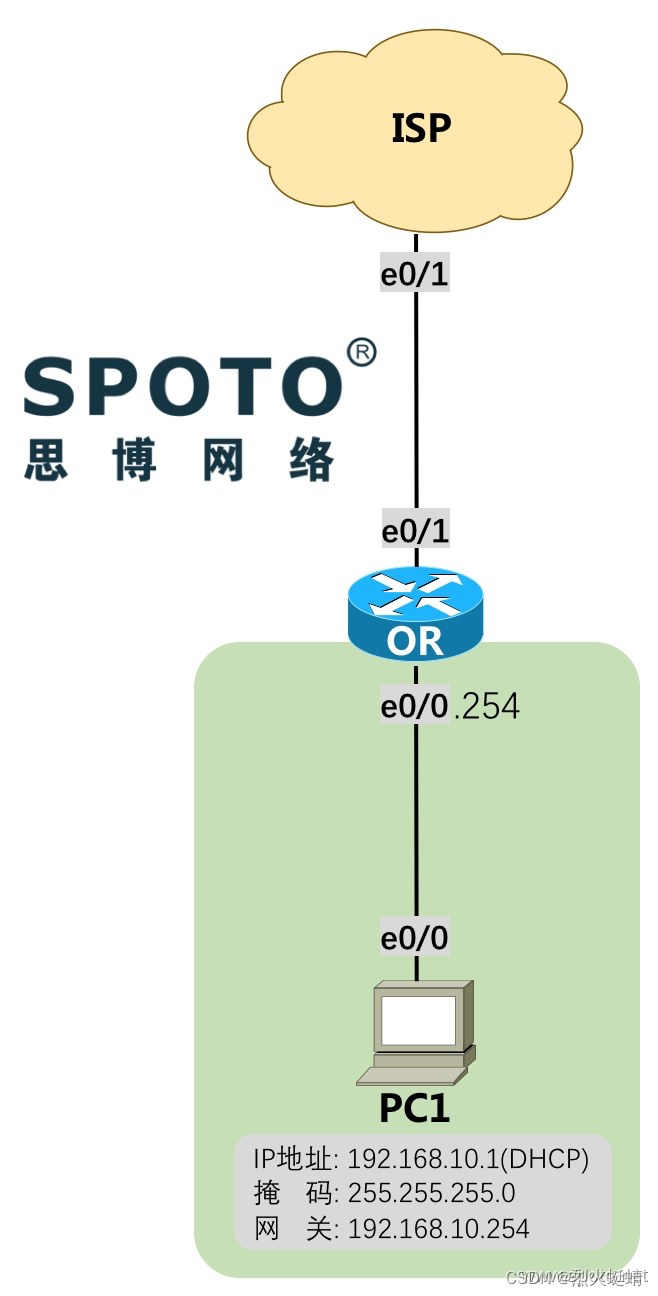
CCNA课程实验-13-PPPoE
目录 实验条件网络拓朴需求 配置实现基础配置模拟运营商ISP配置ISP的DNS配置出口路由器OR基础配置PC1基础配置 出口路由器OR配置PPPOE拨号创建NAT(PAT端口复用) PC1测试结果 实验条件 网络拓朴 需求 OR使用PPPoE的方式向ISP发送拨号的用户名和密码,用户名…...
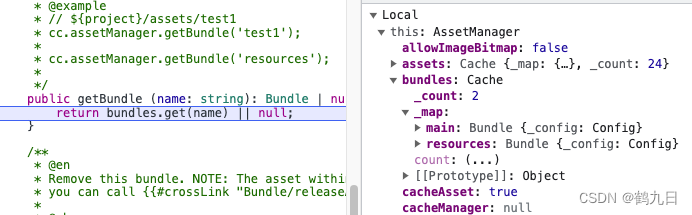
cocosCreator 之 Bundle使用
版本: v3.4.0 语言: TypeScript 环境: Mac Bundle简介 全名 Asset Bundle(简称AB包),自cocosCreator v2.4开始支持,用于作为资源模块化工具。 允许开发者根据项目需求将贴图、脚本、场景等资源划分在 Bundle 中&am…...

分类网络搭建示例
搭建CNN网络 本章我们来学习一下如何搭建网络,初始化方法,模型的保存,预训练模型的加载方法。本专栏需要搭建的是对分类性能的测试,所以这里我们只以VGG为例。 请注意,这里定义的只是一个简陋的版本,后续一…...

为 Ubuntu 虚拟机构建 SSH 服务器
以校园网环境和VMware为例,关键步骤如下: 安装 SSH 服务: 打开 Ubuntu 虚拟机。打开终端。输入命令 sudo apt-get update 更新软件包列表。输入命令 sudo apt-get install openssh-server 安装 SSH 服务。 配置 SSH 服务: 编辑配…...
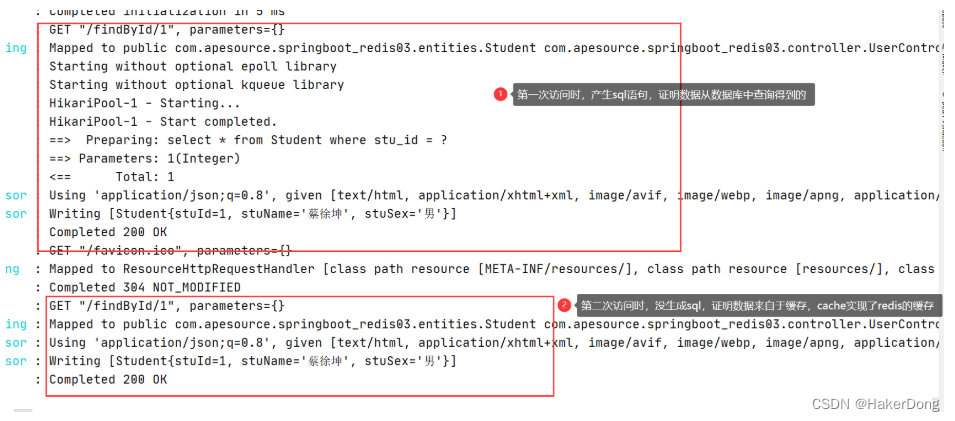
SpringBoot--中间件技术-2:整合redis,redis实战小案例,springboot cache,cache简化redis的实现,含代码
SpringBoot整合Redis 实现步骤 导pom文件坐标 <!--redis依赖--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency>yaml主配置文件,配置…...

linux rsyslog配置文件详解
1.rsyslog配置文件简介 linux rsyslog配置文件/etc/rsyslog.conf分为三部分:MODULES、GLOBAL DIRECTIVES、RULES ryslog模块说明 模块说明MODULES指定接收日志的协议和端口。若要配置日志服务器,则需要将相应的配置项注释去掉。GLOBAL DIRECTIVES主要用来配置日志模版。指定…...

wordpress是什么?快速搭网站经验分享
作者主页 📚lovewold少个r博客主页 ⚠️本文重点:c入门第一个程序和基本知识讲解 👉【C-C入门系列专栏】:博客文章专栏传送门 😄每日一言:宁静是一片强大而治愈的神奇海洋! 目录 前言 wordp…...
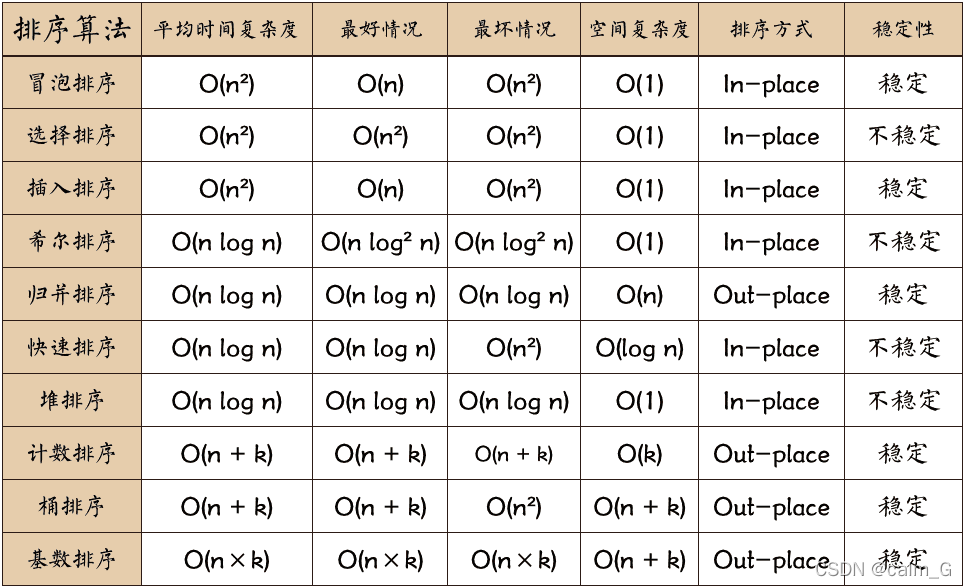
排序 算法(第4版)
本博客参考算法(第4版):算法(第4版) - LeetBook - 力扣(LeetCode)全球极客挚爱的技术成长平台 本文用Java实现相关算法。 我们关注的主要对象是重新排列数组元素的算法,其中每个元素…...
asp.net 在线音乐网站系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net 在线音乐网站系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语言 开发 asp.net 在线音乐网站系统1 应用…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
