2023亚太杯数学建模C题思路
文章目录
- 0 赛题思路
- 1 竞赛信息
- 2 竞赛时间
- 3 建模常见问题类型
- 3.1 分类问题
- 3.2 优化问题
- 3.3 预测问题
- 3.4 评价问题
- 4 建模资料
- 5 最后
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 竞赛信息
2023年第十三届亚太地区大学生数学建模竞赛(以下简称“竞赛”)是北京图象图形学学会主办的亚太地区大学生学科类竞赛,竞赛由亚太地区大学生数学建模竞赛组委会负责组织,欢迎各高等院校按照竞赛章程及有关规定组织同学报名参赛。
2022年第十二届亚太地区大学生数学建模竞赛共有9700支队伍969所高校2万7千多名学生报名参赛。参赛高校覆盖北京大学、清华大学、浙江大学、同济大学、上海交通大学、复旦大学、四川大学、大连理工大学等全部的39所985高校和114所211高校。
除中国大陆高校外,本次参赛队伍还有来自美国的加州大学伯克利分校、约翰斯霍普金斯大学、纽约大学;英国的密德萨斯大学、牛津大学、利物浦大学、诺丁汉大学、爱丁堡大学;德国的亚琛工业大学、 北黑森应用技术大学;俄罗斯的圣彼得堡国立建筑大学;澳大利亚的墨尔本大学、悉尼大学;马来西亚的马来亚大学;日本的東北大学;法国的巴黎先贤祠-阿萨斯大学;澳门地区的澳门城市大学、澳门科技大学、澳门理工学院、澳门大学;香港地区的北京师范大学-香港浸会大学联合国际学院、香港中文大学、香港科技大学、香港理工大学;中外合作的宁波诺丁汉大学、深圳北理莫斯科大学、西安交通利物浦大学等高校。
目前竞赛具有较高的国际影响力,在国内高校中是作为美赛热身赛、保研加分、综合测评加分、创新奖学金等评定竞赛之一。
2 竞赛时间
报名结束时间:2023年11月22日
比赛开始时间:2023年11月23日(周四)6:00
比赛结束时间:2023年11月27日(周一)9:00
3 建模常见问题类型
趁现在赛题还没更新,A君给大家汇总一下数学建模经常使用到的数学模型,题目八九不离十基本属于一下四种问题,对应的解法A君也相应给出
分别为:
分类模型
优化模型
预测模型
评价模型
3.1 分类问题
判别分析:
又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数;用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标;据此即可确定某一样本属于何类。当得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。
聚类分析:
聚类分析或聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
聚类分析本身不是某一种特定的算法,而是一个大体上的需要解决的任务。它可以通过不同的算法来实现,这些算法在理解集群的构成以及如何有效地找到它们等方面有很大的不同。
神经网络分类:
BP 神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。RBF(径向基)神经网络:径向基函数(RBF-Radial Basis Function)神经网络是具有单隐层的三层前馈网络。它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。感知器神经网络:是一个具有单层计算神经元的神经网络,网络的传递函数是线性阈值单元。主要用来模拟人脑的感知特征。线性神经网络:是比较简单的一种神经网络,由一个或者多个线性神经元构成。采用线性函数作为传递函数,所以输出可以是任意值。自组织神经网络:自组织神经网络包括自组织竞争网络、自组织特征映射网络、学习向量量化等网络结构形式。K近邻算法: K最近邻分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
3.2 优化问题
线性规划:
研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。它是运筹学的一个重要分支,广泛应用于生产计划、物流运输、资源分配、金融投资等领域。建模方法:列出约束条件及目标函数;画出约束条件所表示的可行域;在可行域内求目标函数的最优解及最优值。
整数规划:
规划中的变量(全部或部分)限制为整数,称为整数规划。若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性,二次和非线性的整数规划。
非线性规划:
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划研究一个 n元实函数在一组等式或不等式的约束条件下的极值问题,且 目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是 线性函数的情形则属于线性规划。
动态规划:
包括背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等。
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
多目标规划:
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。任何多目标规划问题,都由两个基本部分组成:
(1)两个以上的目标函数;
(2)若干个约束条件。有n个决策变量,k个目标函数, m个约束方程,则:
Z=F(X)是k维函数向量,Φ(X)是m维函数向量;G是m维常数向量;
3.3 预测问题
回归拟合预测
拟合预测是建立一个模型去逼近实际数据序列的过程,适用于发展性的体系。建立模型时,通常都要指定一个有明确意义的时间原点和时间单位。而且,当t趋向于无穷大时,模型应当仍然有意义。将拟合预测单独作为一类体系研究,其意义在于强调其唯“象”性。一个预测模型的建立,要尽可能符合实际体系,这是拟合的原则。拟合的程度可以用最小二乘方、最大拟然性、最小绝对偏差来衡量。
灰色预测
灰色预测是就灰色系统所做的预测。是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
马尔科夫预测:是一种可以用来进行组织的内部人力资源供给预测的方法.它的基本 思想是找出过去人事变动的 规律,以此来推测未来的人事变动趋势.转换矩阵实际上是转换概率矩阵,描述的是组织中员工流入,流出和内部流动的整体形式,可以作为预测内部劳动力供给的基础.
BP神经网络预测
BP网络(Back-ProPagation Network)又称反向传播神经网络, 通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
支持向量机法
支持向量机(SVM)也称为支持向量网络[1],是使用分类与回归分析来分析数据的监督学习模型及其相关的学习算法。在给定一组训练样本后,每个训练样本被标记为属于两个类别中的一个或另一个。支持向量机(SVM)的训练算法会创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器(尽管在概率分类设置中,存在像普拉托校正这样的方法使用支持向量机)。支持向量机模型将样本表示为在空间中的映射的点,这样具有单一类别的样本能尽可能明显的间隔分开出来。所有这样新的样本映射到同一空间,就可以基于它们落在间隔的哪一侧来预测属于哪一类别。
3.4 评价问题
层次分析法
是指将一个复杂的 多目标决策问题 作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
优劣解距离法
又称理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最大值和最小值,通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
模糊综合评价法
是一种基于模糊数学的综合评标方法。 该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。 它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色关联分析法(灰色综合评价法)
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
典型相关分析法:是对互协方差矩阵的一种理解,是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
主成分分析法(降维)
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。
因子分析法(降维)
因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
BP神经网络综合评价法
是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
4 建模资料
资料分享: 最强建模资料


5 最后
相关文章:

2023亚太杯数学建模C题思路
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料5 最后 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 2023年第十三…...

【ArcGIS Pro微课1000例】0030:ArcGIS Pro中自带晕渲地貌工具的妙用
在ArcGIS中,制作地貌晕渲效果通常的做法是先制作山体阴影效果,然后叠加在DEM的下面,再改变DEM的透明度来实现。而在ArcGIS Pro中自带了效果显著的晕渲地貌工具。 文章目录 一、晕渲地貌工具1. 符号系统2. 栅格函数二、山体阴影效果1. 工具箱2. 栅格函数打开ArcGIS Pro3.0,加…...
【原创】java+swing+mysql办公用品管理系统设计与实现
摘要: 办公用品管理系统是一个设计和实现办公用品库存和使用管理的信息系统。此系统可以提高办公用品的利用率,减少浪费,使办公用品管理更加高效、规范、便捷。本文主要介绍使用javaswingmysql技术去开发实现一个办公用品管理系统。 功能分…...

sqlalchemy查询数据为空,查询范围对应的数据在数据库真实存在
记录一个开发过程遇到的小bug,构造些伪数据还原并解释。 """ 场景:传参触发了查询条件,数据库中是存在传参对应范围的数据,但是通过查询条件得到的查询结果为空 """ 入参场景一: start_time = "2023-11-13" end_time = "202…...

Code Former安装及使用
Code Former是南洋理工大学和商汤科技联合研究中心联合开发一款AI人脸修复算法,通过该算法,可以对已经模糊的图片进行人脸修复,找回斑驳的记忆 由于网上对于Code Former的封装,全都是要花钱,或者需要其他什么曲折的方式…...

SpringMVC--@RequestMapping注解
RequestMapping注解 RequestMapping注解的功能RequestMapping注解的位置RequestMapping注解的属性1、value属性2、method属性3、params属性(了解) 补充RequestParamRequestHeaderRequestBody RequestBody获取json格式的请求参数 ResponseBodyRestControl…...
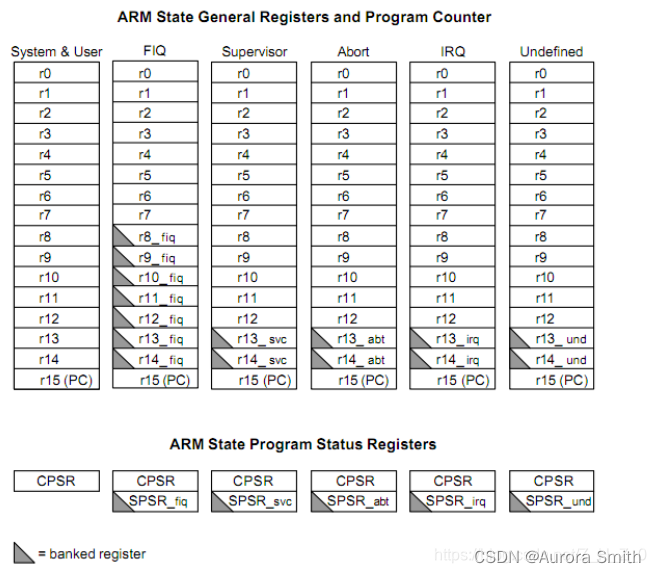
ARM寄存器及功能介绍/R0-R15寄存器
1、ARM 寄存器组介绍 ARM 处理器一般共有 37 个寄存器,其中包括: (1) 31 个通用寄存器,包括 PC(程序计数器)在内,都是 32 位的寄存器。 (2) 6 个状态寄存器…...
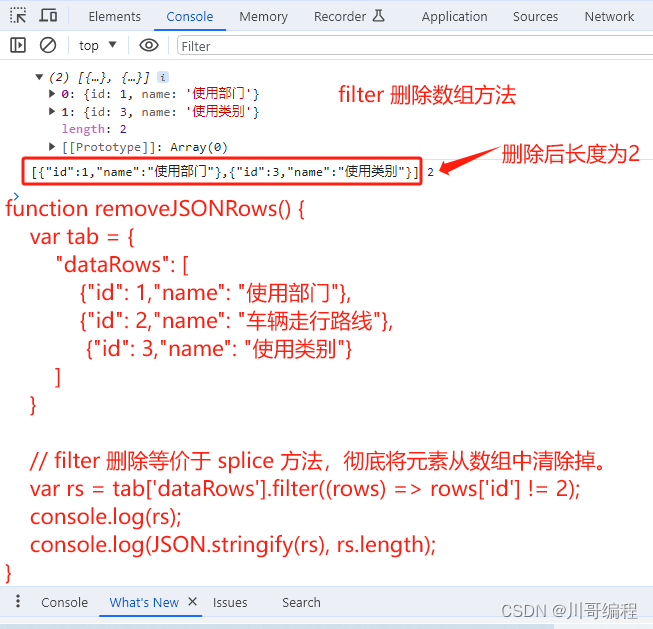
js删除json数据中指定元素
delete 删除数组方法: function removeJSONRows() {var tab {"dataRows": [{"id": 1,"name": "使用部门"},{"id": 2,"name": "车辆走行路线"},{"id": 3,"name": &quo…...

广州华锐互动:VR刑侦现场执法实训助力警察全面提升警务能力
随着科技的不断发展,虚拟现实(VR)技术在多个领域开始得到广泛应用,其中包括公安执法培训。VR刑侦现场执法实训系统是一种采用虚拟现实技术,为公安执法人员提供模拟真实环境的培训工具。通过这种平台,公安人…...
应用程序)
多线程 浏览器渲染引擎 图形用户界面(GUI,Graphical User Interface)应用程序
目录 多线程浏览器渲染引擎图形用户界面(GUI,Graphical User Interface)应用程序 👍 点赞,你的认可是我创作的动力! ⭐️ 收藏,你的青睐是我努力的方向! ✏️ 评论,你的…...
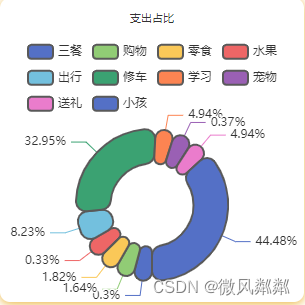
echarts饼图label显示不全原因?
echarts饼图label显示不全原因? 标签数量过多:当饼图的扇形数量较多时,为了保证图形的清晰性,ECharts 可能不会显示所有的标签,而是选择显示部分标签或者不显示标签。标签过长:如果标签的文字过长…...

暖手宝上架亚马逊美国站UL499报告测试标准要求
暖手宝是运用物理及化学原理研制的自动取暖保健用品。该产品以其自动生热,有趣,实用等新颖独特的优势,深受欢迎——暖手宝具有自动取暖,理疗保健等多种功能。只要插上电源等上10分钟左右就能发热,最后一种是通过锂电池…...
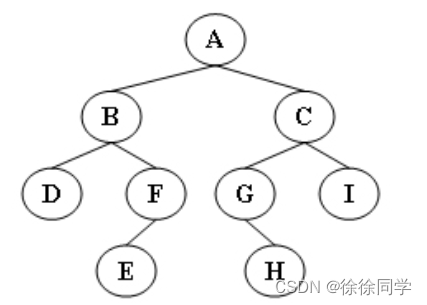
2023数据结构期中测验-2023秋-计算机+未来网络专业
这里写目录标题 选择题函数题6-1 求链式表的表长6-2 逆序数据建立链表6-3 删除单链表偶数节点6-4 求二叉树高度6-5 先序输出叶结点 选择题 2-1 下述程序段的时间复杂度为( ) for(i0; i<n-1; i)for(j0; j<n-1-i…...

解锁内存之谜:从C到Python、Java和Go的内存管理对比
前言 在编程世界中,内存是宝贵的资源,而管理它却是一个复杂的挑战。不同的编程语言以其独特的方式处理内存分配和释放。从C语言的显式malloc和free到Python、Java和Go的自动内存管理,每种语言都有其独特之处。本文将深入探讨各种编程语言中的…...

Redirect:301和302不同场景选择问题
redirect场景,一般来说,会有大量用户在收藏夹里放着你的官网主页。但是用户收藏的url未必会跟着官网url的变动一起自动更新 这个官网主页因为一些其他的原因,需要迁服务器或者换ip等等。所以在换之前要搞一个redirect,把访问引流…...

ChromeDriver谷歌浏览器驱动下载安装与使用最新版118/119/120
ChromeDriver谷歌浏览器驱动下载安装与使用最新版118/119/120 1. 确定Chrome版本 我们首先确定自己的Chrome版本 Chrome设置->关于Chrome 可以看到,当前chrome是最新版本:119.0.6045.124(正式版本) (64 位&#…...
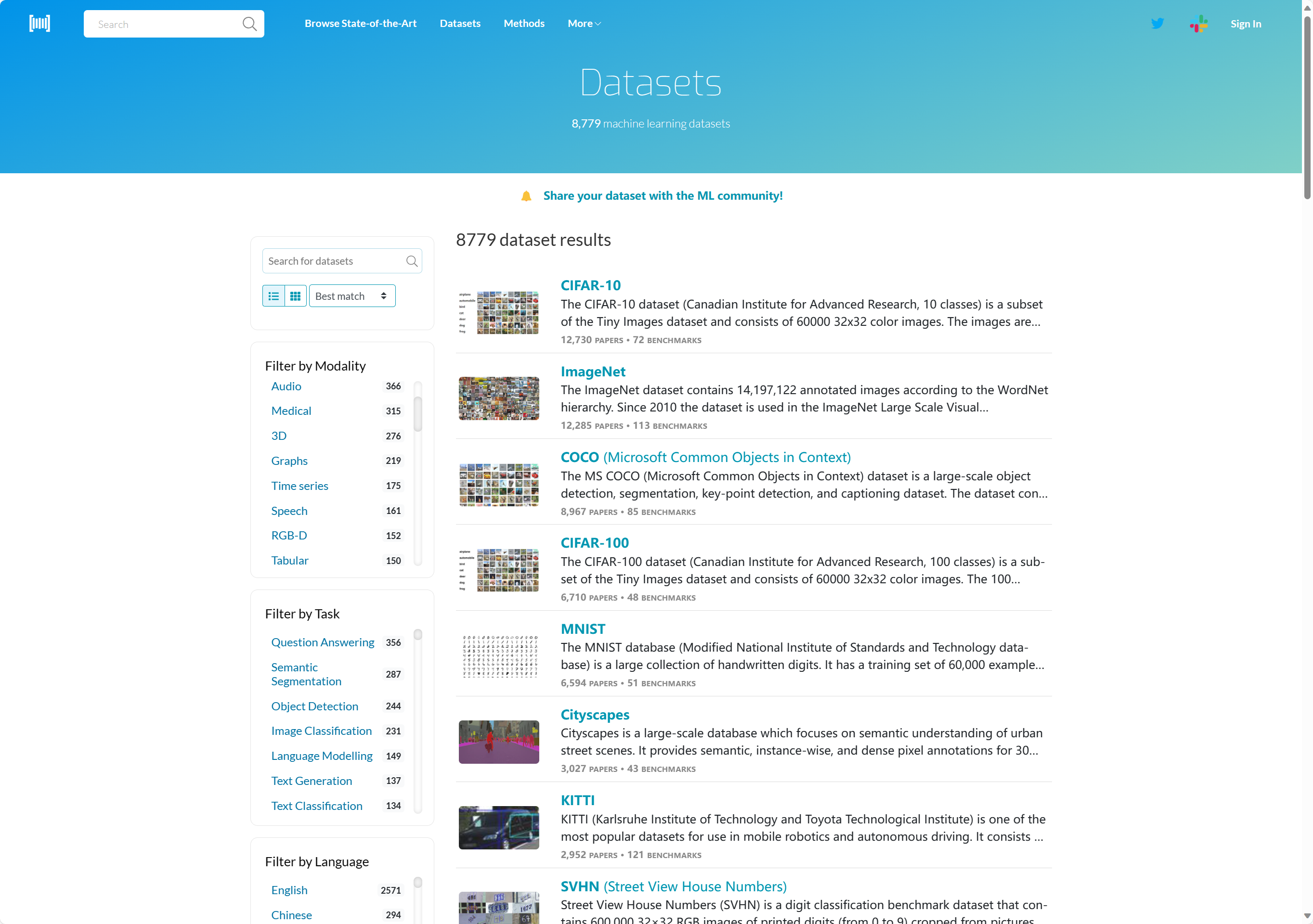
研究生做实验找不到数据集咋办?
做实验找不到数据集咋办?这是很多研究者和开发者都会遇到的问题。数据集是实验的基础,没有合适的数据集,就无法验证模型的性能和效果。那么,有没有什么方法可以快速地找到我们需要的数据集呢?本文将介绍4个常用的数据集搜索平台,希望能够帮助大家解决这个难题。下面以室内…...
说说React diff的原理是什么?
一、是什么 跟Vue一致,React通过引入Virtual DOM的概念,极大地避免无效的Dom操作,使我们的页面的构建效率提到了极大的提升 而diff算法就是更高效地通过对比新旧Virtual DOM来找出真正的Dom变化之处 传统diff算法通过循环递归对节点进行依次对比,效率低下,算法复杂度达…...
:什么是链路追踪?)
链路追踪详解(一):什么是链路追踪?
目录 引言 什么是链路追踪? 链路追踪的重要性 链路追踪在分布式系统中的应用 链路追踪的基本术语 小结 引言 随着云计算、大数据和人工智能等新技术的快速发展,传统的单体式架构已经无法满足快速迭代的需求,因此,微服务架构…...

2024怎么自学软件测试?自动化测试?测试老鸟总结,少走弯路...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、自学软件测试怎…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
