【算法 | 模拟No.4】AcWing 756. 蛇形矩阵 AcWing 40. 顺时针打印矩阵
个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【AcWing算法提高学习专栏】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
原题链接:点击直接跳转到该题目
目录
- 一、AcWing 756. 蛇形矩阵
- 1️⃣题目描述
- 2️⃣题目解析
- 3️⃣解题代码
- 二、AcWing 40. 顺时针打印矩阵
- 1️⃣题目描述
- 2️⃣解题代码
一、AcWing 756. 蛇形矩阵
1️⃣题目描述
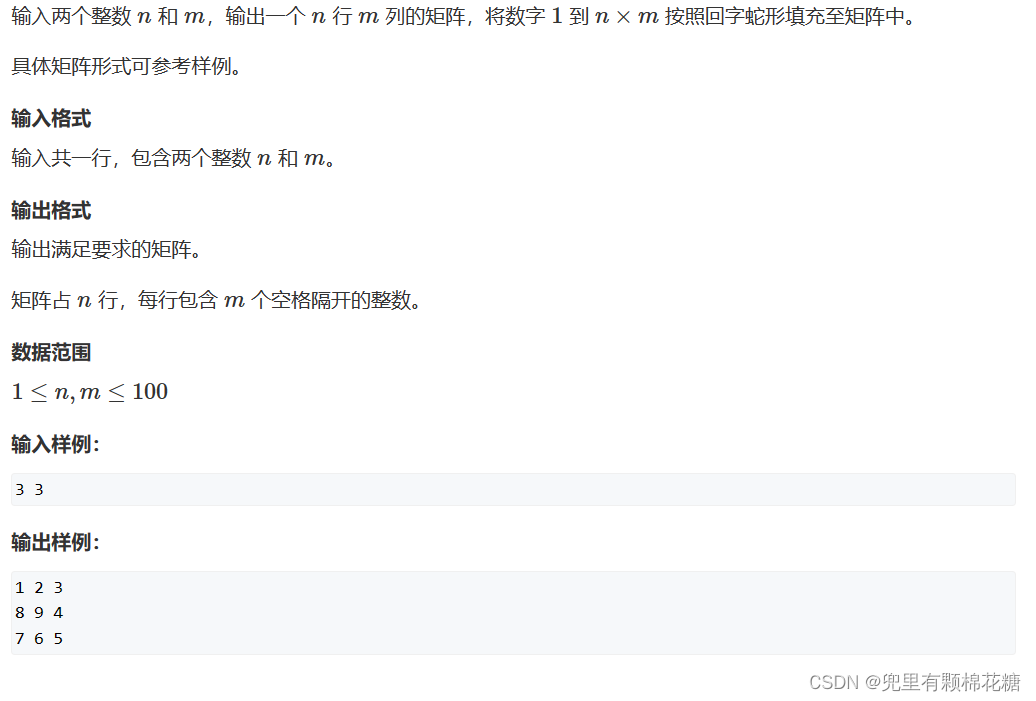
2️⃣题目解析
代码中:dx[] 和 dy[] 数组分别表示了在四个方向上 x 和 y 的变化量。 x 和 y 则是当前要填充的位置坐标, d 则代表方向,初始方向为右(即初始化d为1,代表一开始的时候初始方向为右方向)。
代码先在 x、y 坐标处填充了当前的值 i,然后根据当前方向判断下一个要填的位置坐标。如果下个要填的位置超出边界或者已经被填充过,需要改变方向。
当发生改变方向时,采用了 (d + 1) % 4 的形式来改变方向,其中 % 4 是为了保证方向不超出 4 个。
3️⃣解题代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>const int N = 110;
int arr[N][N];using namespace std;int main()
{int n,m;cin >> n >> m;int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1};int x = 0,y = 0,d = 1; // 这里我们初始化方向为有方向// 总共有4个方向:分别为上下左右,上为0、右为1、下为2、左为3// 这里我们要先把一开始要填的位置,即x = 0,y = 0的位置先提前定义出来for(int i = 1;i <= n * m;i++){arr[x][y] = i;int a = x + dx[d],b = y + dy[d];if(a < 0 || a >= n || b < 0 || b >= m || arr[a][b]){d = (d + 1) % 4;a = x + dx[d],b = y + dy[d];}x = a,y = b; // 这里的x、y即为下一个要填的位置}// 打印最终的矩阵即可for(int i = 0;i < n;i++){for(int j = 0;j < m;j++)printf("%d ",arr[i][j]);cout << endl;}return 0;
}
最后代码就顺利通过啦!!!
二、AcWing 40. 顺时针打印矩阵
1️⃣题目描述
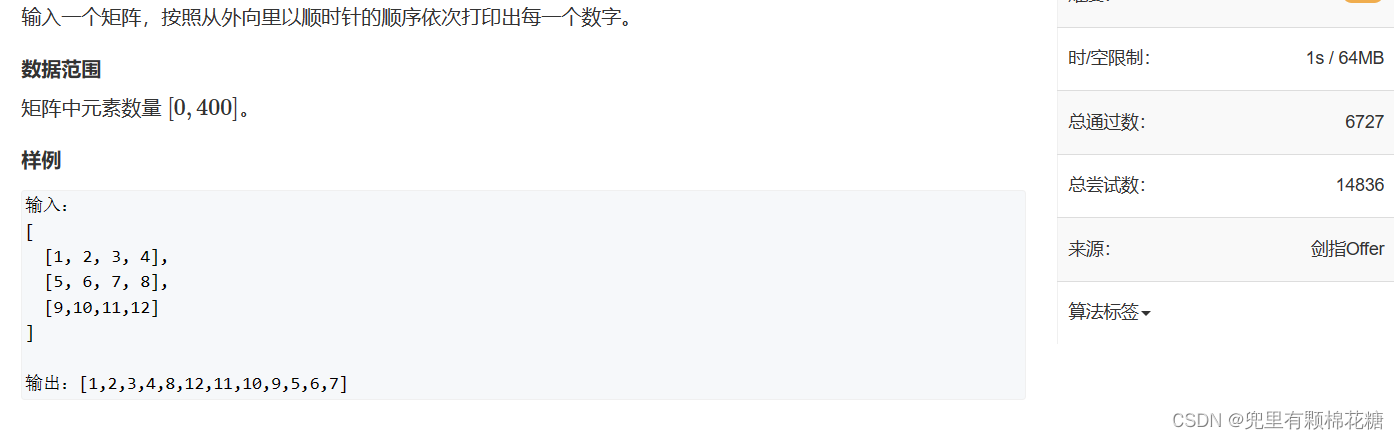
2️⃣解题代码
class Solution {
public:vector<int> printMatrix(vector<vector<int>>& matrix) {vector<int> res;if(matrix.empty()) return res;int n = matrix.size(),m = matrix[0].size();vector<vector<bool>> st(n,vector<bool>(m,false));int x = 0,y = 0,d = 1;int dx[] = {-1,0,1,0},dy[] = {0,1,0,-1};for(int i = 1;i <= n * m;i++){res.push_back(matrix[x][y]);st[x][y] = true;int a = x + dx[d],b = y + dy[d];if(a < 0 || a >= n || b < 0 || b >= m || st[a][b]){d = (d + 1) % 4;a = x + dx[d],b = y + dy[d];}x = a,y = b;}return res;}
};
最后就是顺利通过啦!!!
相关文章:

【算法 | 模拟No.4】AcWing 756. 蛇形矩阵 AcWing 40. 顺时针打印矩阵
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【AcWing算法提高学习专栏】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程&a…...

数据——最为直接的答案
身处于这样一个数字化快速发展、竞争强烈的时代,不管是企业还是个人,大家都需要及时获取前沿动态信息,密切关注市场的变化。但是,在不计其数的企业中,到底行业top 是哪些企业引领潮流? 只有数据能告诉你最…...

php加密解密的用法(对称加密,非对称加密)
加密和摘要的区别 ***摘要:是从已知的数据中,通过摘要计算出一个值,一个数据对应一个或多个摘要的值 *** 比如:md5 和 sha1 sha256 hash 就是得到一个特定的值 ,同一个数据得到的md5 是一样的,不会改变的 比…...
优秀智慧园区案例 - 中建科技产业园(中建·光谷之星),万字长文解析先进智慧园区建设方案经验
一、项目背景 中建科技产业园(中建光谷之星),位于武汉光谷中心城、中国(湖北)自贸试验区武汉片区双核心区,光谷发展主轴高新大道北侧,建筑面积108万平米,是中建三局“中建之星”和“…...

Python基础详解教程------目录大纲
Python基础详解教程------让编程简单 目录 第一章、python基本概念规范... 5 1.1方法(Method)与函数(Function) 5 1.2类(Class)与函数(Function) 6 1.3变量(Variable)与参数(Parameter)及形参与实参... 7 1.4变量(Variable)与属性(Attribute)及property. 8 1.5对象(Objec…...

什么是高防IP?
什么是高防IP? 高防IP是针对互联网服务器在遭受大流量的DDOS攻击后导致服务不可用的情况下,推出的付费增值服务,用户可以通过配置高防IP,将攻击流量引流到高防IP,确保源站的稳定可靠。(无需转移数据&#…...
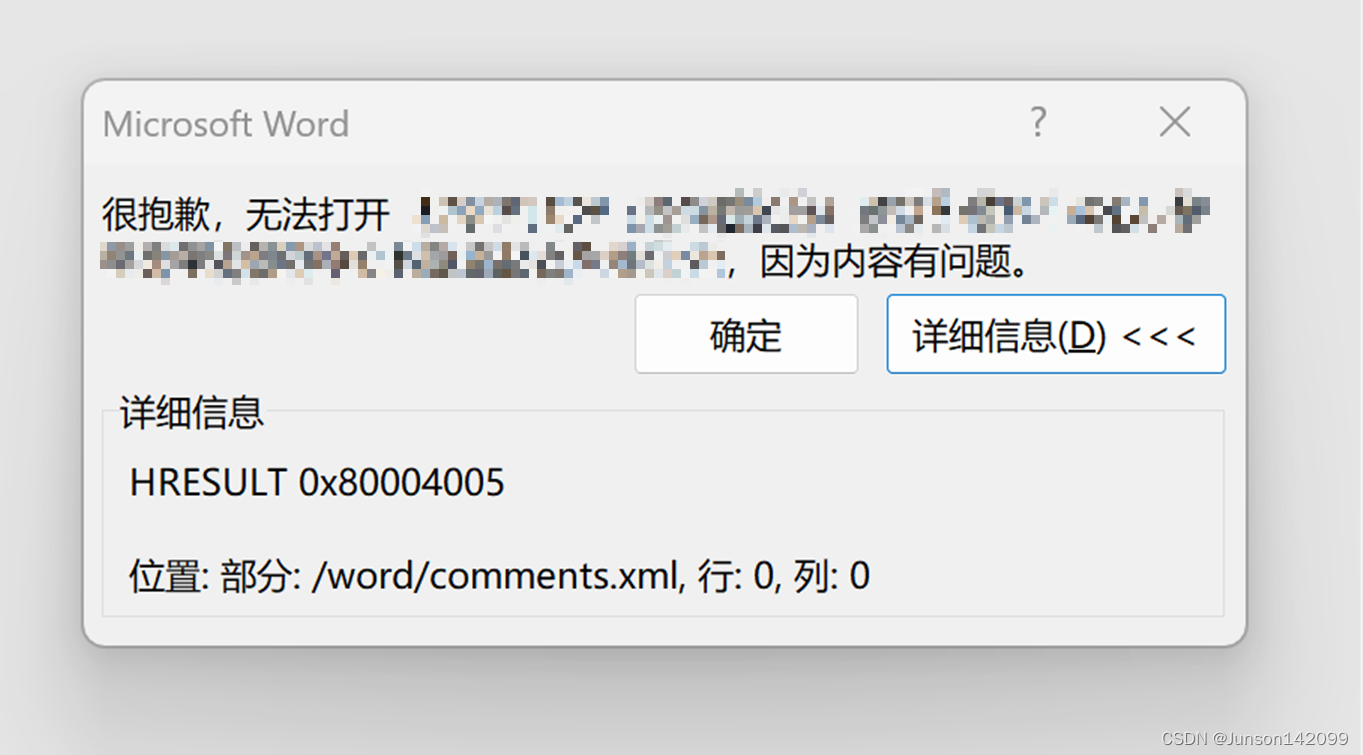
打开word文档报错,提示HRESULT 0x80004005 位置: 部分: /word/comments.xml,行: 0,列: 0
某用户遇到这样一个奇怪的问题,就是回复完word的批注后,保存文档再打开就会报错,提示很抱歉,无法打开XXX,因为内容有问题。,详细信息提示HRESULT 0x80004005 位置: 部分: /word/comments.xml,行: 0,列: 0 c…...
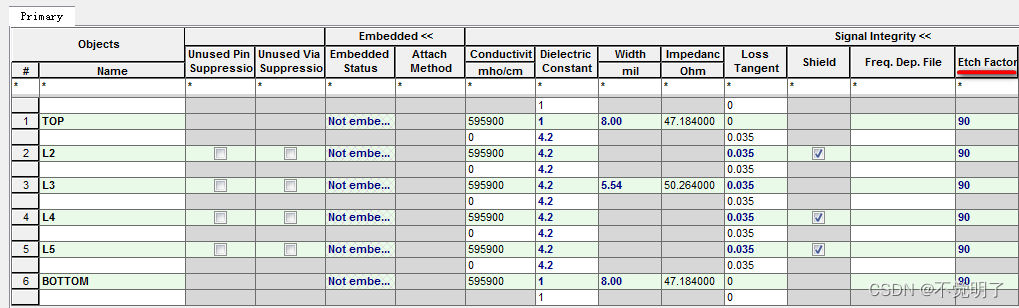
Allegro层叠中的Etch Factor-铜皮的腐蚀因子如何计算
Allegro层叠中的Etch Factor-铜皮的腐蚀因子如何计算 在用Allegro进行PCB设计的时候,Cross-section中需要填入对应的信息,一般填入每层的厚度即可,如下图 当PCB需要进行仿真分析的时候,Etch-Factor这个值是必须要填写的,如下图 目前看到的都是90这个值,这是一个理论值。 …...

20 个好用的一行 Java代码
今天分享给大家20个 令人惊叹的 Java一行代码,让你们的工作更轻松。一起来看看吧! 1. 获取浏览器 Cookie 的值 使用document.cookie 来获取 Cookie 的值。 2. 将 RGB 转换为十六进制 3. 复制到剪贴板 使用 navigator.clipboard.writeText 轻松将任何文本…...

Java编程--单例模式(饿汉模式/懒汉模式)/阻塞队列
前言 逆水行舟,不进则退!!! 目录 单例模式 饿汉模式: 懒汉模式: 什么是阻塞队列 什么是高内聚 低耦合 阻塞队列的实现 单例模式 单例模式(Singleton Pattern)是一种常见…...

【go-zero】go-zero 脚手架 simple-admin 第二章:通过goctls生成api整个项目
往期回顾 一、simple-admin 开篇:安装 了解 goctls 二、go-zero 脚手架 simple-admin 第一章:通过goctls生成rpc整个项目 | go-zero整合 ENT数据库orm框架 本章内容 往期回顾一、simple-admin 创建rpc项目实战1、创建git仓库1.1、创建任意git仓库1.2、克隆到本地2、创建API项…...

小程序用户隐私设置指引
自2021年11月1日起,个人信息保护法正式执行了。微信小程序在这方面也加强了整改。小程序对涉及个人隐私使用的需要严格要求修改,不修正的小程序将被下架风险;新上线的小程序也要完善小程序个人隐私设置,不然代码提交不会通过。 小…...

Docker - 容器数据卷
Docker - 容器数据卷 什么是容器数据卷 等同于挂载,将容器内的目录地址指向于宿主机文件系统中 直接使用命令来挂载 -v docker run -it -v 主机目录:容器内目录# 测试 docker run -it -v /root:/home centos /bin/bash [rootiZ2zeg7mctvft5renx1qvbZ ~]# docker …...

YOLOv5独家最新改进《新颖高效AsDDet检测头》VisDrone数据集mAP涨点,即插即用|检测头新颖改进,性能高效涨点
💡本篇内容:YOLOv5独家最新改进《新颖高效AsDDet检测头》VisDrone数据集mAP涨点1.4%,即插即用|检测头新颖改进,性能高效涨点 💡🚀🚀🚀本博客 YOLO系列 + 全新新颖原创高效AsDDet检测头 改进创新点改进源代码改进 适用于 YOLOv5 按步骤操作运行改进后的代码即可…...

第十三章 网络管理实战1
第十三章 网络管理实战1 1osl模型 1.1简介 开发系统互联模型 开放式系统互联 国际标准化组织 ISO 指定定义了不同计算机互联的标准设计和描述 计算机网络通信的框架设计和描述 计算机网络通信的框架 全世界网络通信的工作分为7层 应用层表示层会话层传输层网络层数据链路…...

警惕!.360、.halo病毒来袭,这些建议能让你的数据安如泰山!
导言: 嘿,亲爱的读者们,今天91数据恢复讨论一个挑战性极高的问题——.halo、.360病毒,这可是个十足的恶棍,专门对你珍贵的数据下黑手!别怕,我这就告诉你怎么防患于未然,还有被它拐走…...

ubuntu使用快照部署polygon全节点
文章目录 一、 环境部署1.1 golang环境部署1.2 git安装1.3 gcc安装1.4 zstd 安装1.5 pv 安装1.6 aria2c 安装二、安装 polygon2.1 heimdall 安装2.1.1 heimdall 编译2.1.2 初始化 heimdall2.1.3 修改配置文件2.2 bor 安装2.2.1 bor 编译2.2.2 创建bor数据目录2.2.3 修改配置文件…...
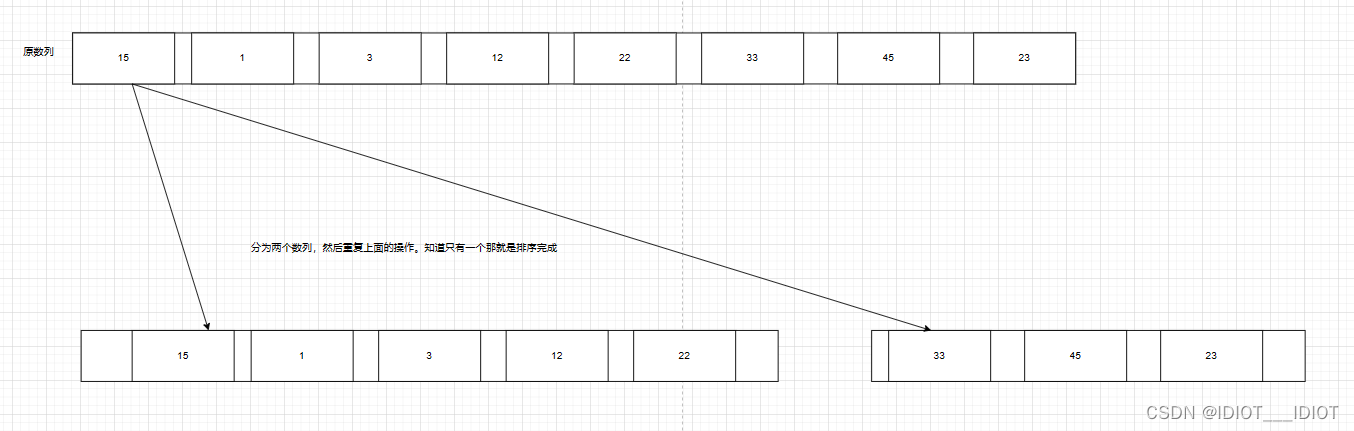
理解快速排序
理解快速排序 首先了解以下快速排序 快速排序(QuickSort)是一种常用的排序算法,属于比较排序算法的一种。它是由英国计算机科学家Tony Hoare于1960年提出的,是一种分而治之(divide and conquer)的算法。 …...
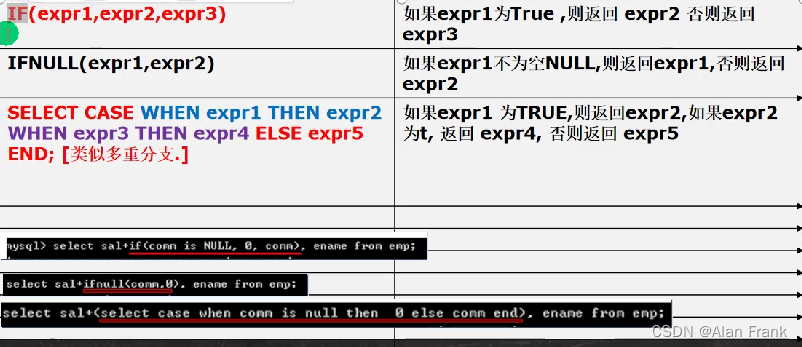
初始MySQL(三)(合计函数,分组函数,字符串相关函数,数字相关函数,时间日期函数,加密函数,流程控制函数)
目录 合计/统计函数 count 返回行的总数 sum 合计函数 - avg group by 字符串相关函数 数学相关函数 时间日期相关函数 加密函数 流程控制函数 合计/统计函数 count 返回行的总数 Select count(*) | count (列名) from tablename [WHERE where_definition] #演…...
AI系统ChatGPT源码+详细搭建部署教程+AI绘画系统+支持GPT4.0+Midjourney绘画+已支持OpenAI GPT全模型+国内AI全模型
一、AI创作系统 SparkAi创作系统是基于OpenAI很火的ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
