【C语言数据结构————————二叉树】
文章目录
-
文章目录
-
一、什么是树
-
树的定义
-
树的种类
-
树的深度
-
树的基本术语
-
-
二、满二叉树
-
定义
-
满二叉树的特点
-
-
三、完全二叉树
-
定义
-
特点
-
-
四、二叉树的性质
-
五、二叉树的存储结构
-
顺序存储结构
-
链式存储结构
-
-
六、二叉树的基本操作
-
七、二叉树的创建
-
八、二叉树的遍历
-
前序遍历
-
中序遍历
-
后序遍历
-
-
九、二叉树的销毁
-
十、二叉树中节点的查找
欢迎阅读新一期的c语言数据结构模块————二叉树
✒️个人主页:-_Joker_-
🏷️专栏:C语言数据结构
📜代码仓库:c_code
🌹🌹欢迎大佬们的阅读和三连关注,顺着评论回访🌹🌹
一、什么是树
1.树的定义
树是n(n>=0)个结点的有限集。当n = 0时,称为空树。在任意一棵非空树中应满足:
- 有且仅有一个特定的称为根的结点。
- 当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1,T2,…,Tm,其中每个集合本身又是一棵树,并且称为根的子树。
2.树的种类
树的种类可以分为以下几种
- 无序树:树中任意节点的子结点之间没有顺序关系,这种树称为无序树,也称为自由树;
- 有序树:树中任意节点的子结点之间有顺序关系,这种树称为有序树;
- 二叉树:每个节点最多含有两个子树的树称为二叉树;
- 满二叉树:叶节点除外的所有节点均含有两个子树的树被称为满二叉树;
- 完全二叉树:除最后一层外,所有层都是满节点,且最后一层缺右边连续节点的二叉树称为完全二叉树;
- 哈夫曼树(最优二叉树):带权路径最短的二叉树称为哈夫曼树或最优二叉树。
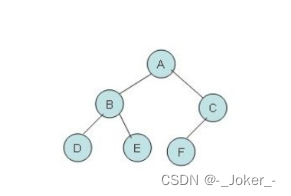
3.树的深度
定义一棵树的根结点层次为1,其他结点的层次是其父节点层次加1。一棵树中所有结点的层次的最大值称为这棵树的深度。例如:
如图,图中的树的深度为:3
4.树的基本术语
- 结点的度:结点拥有的子树数目
- 叶子(终端)结点:度为0的结点
- 分支(非终端)结点:度不为0的结点
- 树的度:树的各结点度的最大值
- 内部结点:除根结点之外的分支结点
- 双亲与孩子结点:结点的子树的根称为该结点的孩子;该结点称为孩子的双亲
- 兄弟:属于同一双亲的孩子
- 结点的祖先:从根到该结点所经分支上的所有结点
- 结点的子孙:该结点为根的子树中的任一结点
- 结点的层次:表示该结点在树中的相对位置。根为第一层,其他的结点依次下推;若
- 结点在第L层上,则其孩子在第L+1层上
- 兄弟节点:双亲在同一层的结点互为兄弟节点
- 树的深(高)度:树中结点的最大层次
- 有序树:树中各结点的子树从左至右是有次序的,不能互换。否则,称为无序树
- 路径长度:从树中某结点Ni出发,能够“自上而下”通过树中结点到达结点Nj,则称Ni到Nj存在
- 一条路径,路径长度等于这两个结点之间的分支数
- 树的路径长度:从根到每个结点的路径长度之和。
- 森林:是m(m≥0)棵互不相交的树的集合
由于二叉树的使用在数据结构中更加广泛,所以我们以二叉树为主来进行讲解,下面介绍一下关于二叉树的基本知识。
二、满二叉树
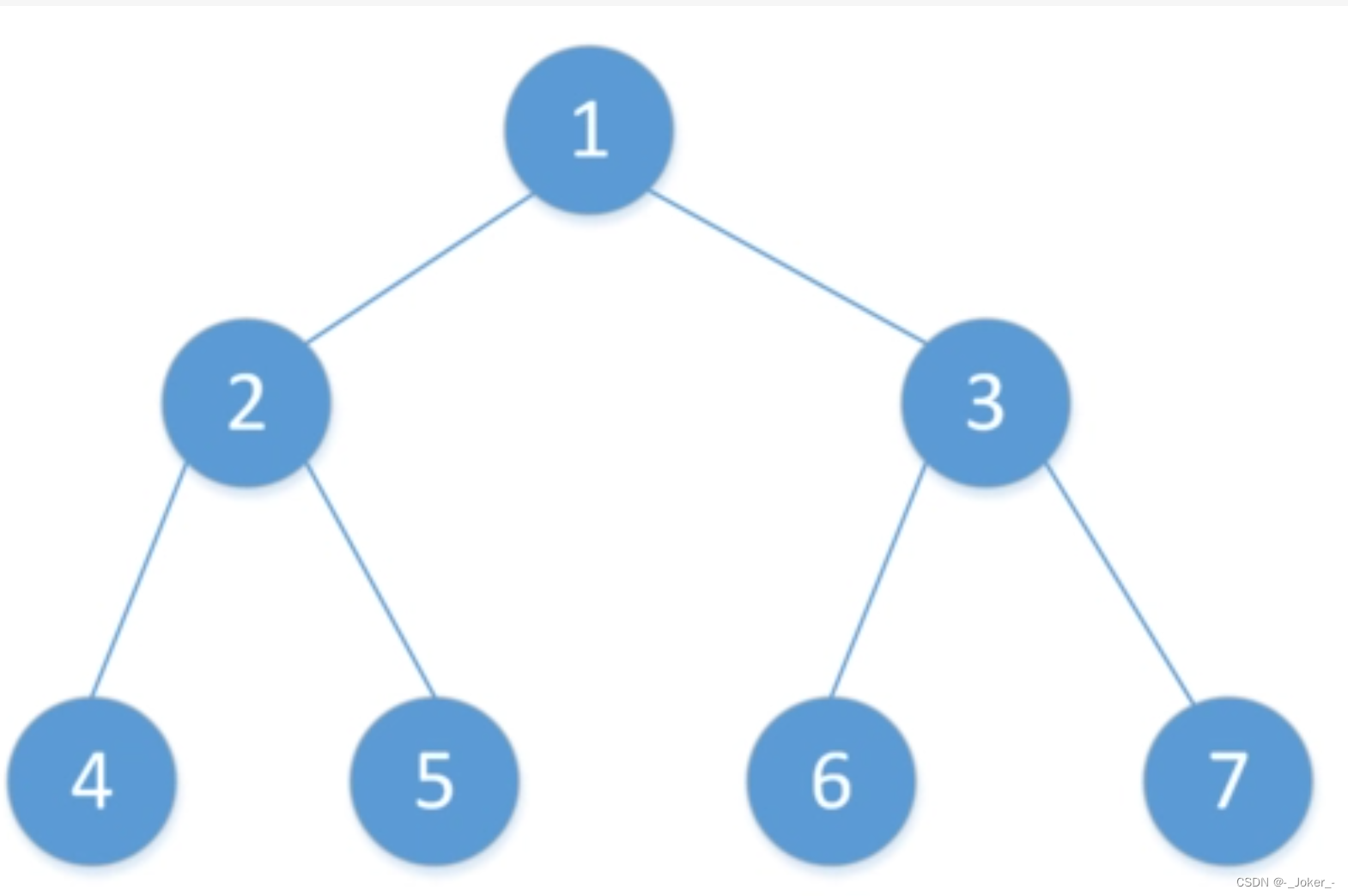
定义:
二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子节点都在同一层上,这样的二叉树称为满二叉树。
如图为一颗满二叉树
满二叉树的特点
满二叉树的特点有:
- 叶子节点只能出现在最下一层。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
- 设树的深度为i,则总结点数为 2^i -1
- 满二叉树是一种特殊的完全二叉树
- 若有双亲,则其双亲为i / 2,若有左孩子,则左孩子为2i ,若有右孩子,则右孩子为2i + 1 。
三、完全二叉树
定义
对二叉树节点由左至右由上至下的编号,如果编号为i的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
如图为一颗完全二叉树
特点
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即没有右子树。
- 同样结点数目的二叉树,完全二叉树深度最小。
- 满二叉树一定是完全二叉树,但反过来不一定成立。
四、二叉树的性质
- 二叉树的第i层上至多有2^(i-1) (i≥1)个结点
- 深度为k的二叉树至多有2^k-1个结点(k≥1)
- 对任何一棵二叉树T,如果其终端结点数为N0,度为2的结点数为N2,则N0=N2+1
- 具有n个结点的完全二叉树的深度为[log2(n)]+1
- 一棵具有n个结点的完全二叉树(又称顺序二叉树)对其结点按层从上至下(每层从左至右)进行1-n的编号,则对任一结点i(1≤i≤n)有:
- 若i>1,则i的双亲是[i/2];若i=1,则i是根,无双亲。
- 若2i≤n,则i的左孩子是2i;否则,i无左孩子
- 若2i+1≤n,则i的右孩子是2i+1;否则,i无右孩子
五、二叉树的储存结构
二叉树的储存结构分为顺序存储结构和链式存储结构
顺序存储结构
二叉树的顺序存储是指用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为i ii的结点元素存储在一维数组下标为 i − 1的分量中。
依据二叉树的性质,完全二叉树和满二叉树采用顺序存储比较合适,树中结点的序号可以唯一地反映结点之间的逻辑关系,这样既能最大可能地节省存储空间,又能利用数组元素的下标值确定结点在二叉树中的位置,以及结点之间的关系。
但对于一般的二叉树,为了让数组下标能反映二叉树中结点之间的逻辑关系,只能添加一些并不存在的空结点,让其每个结点与完全二叉树上的结点相对照,再存储到一维数组的相应分量中。然而,在最坏情况下,一个高度为h 且只有h 个结点的单支树却需要占据近2h-1个存储单元。二叉树的顺序存储结构如图所示,其中0表示并不存在的空结点。
链式存储结构
由于顺序储存结构非常不便,所以我们通常采用链式存储结构实现二叉树。链式存储结构通过开辟一块空间(节点),通过指针储存左孩子、右孩子节点以及数据。
由于顺序结构操作起来并不方便,所以我们通常都以链式存储结构通过递归来实现二叉树,定义如下
typedef struct BinaryTree
{int val;struct BinaryTree *left;struct BinaryTree *right;
}BT;六、二叉树的基本操作
- CreateTree() :创建二叉树
- PreOrder(BT* root):二叉树的前序遍历
- InOrder(BT* root): 二叉树的中序遍历
- BackOrder(BT* root): 二叉树的后序遍历
- DestoryTree(BT* root):销毁二叉树
- FindTree(BT* root, int x):查找二叉树中值为x的节点
七、二叉树的创建
如下是对二叉树进行创建的算法
BTNode* CreatNode(int x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");exit(-1);}node->val = x;node->left = NULL;node->right = NULL;return node;
}八、二叉树的遍历
前序遍历
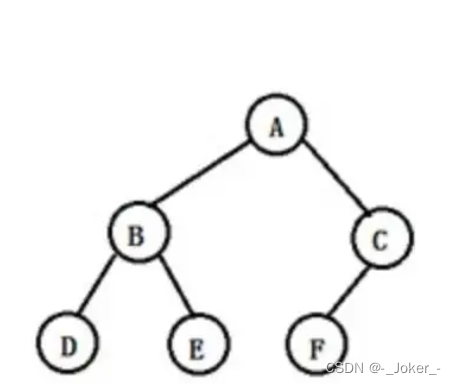
二叉树的前序遍历顺序为根 - 左 - 右
即先访问根节点
然后访问其左孩子节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:A -> B -> D -> E -> C -> F
算法如下
void PreOrder(BT* root)
{if (root == NULL){return;}printf("%d",root->val);PreOrder(root->left);PreOrder(root->right);
}中序遍历
二叉树的前序遍历顺序为左 - 根 - 右
即先访问左孩子节点
然后访问其根节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:D -> B -> E -> A -> F -> C
算法如下
void InOrder(BT* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}后序遍历
二叉树的前序遍历顺序为左 - 右 - 根
即先访问左孩子节点
然后访问其根节点
最后访问其右孩子节点
例如上图,前序遍历顺序为:D -> E -> B -> F -> C -> A
算法如下
void BackOrder(BT* root)
{if (root == NULL){return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->val);
}九、二叉树的销毁
二叉树的销毁同样通过递归来实现:
void DestoryTree(BT* root)
{if (root == NULL){return;}DestoryTree(root->left);DestoryTree(root->right);free(root);
}
十、二叉树中节点的查找
BT* FindTree(BT* root, int x)
{if (root == NULL){return;}if (root->val == x)return root;FindTree(root->left, x);FindTree(root->right, x);return NULL;
}相关文章:
【C语言数据结构————————二叉树】
文章目录 文章目录 一、什么是树 树的定义 树的种类 树的深度 树的基本术语 二、满二叉树 定义 满二叉树的特点 三、完全二叉树 定义 特点 四、二叉树的性质 五、二叉树的存储结构 顺序存储结构 链式存储结构 六、二叉树的基本操作 七、二叉树的创建 八、二叉树…...
分组取每组数据的最大值和最小值的方法思路,为类似场景的数据分析提取提供思路,例如提取宗地内建筑的最高层数等可参考此方法思路
目录 一、实现效果 二、实现过程 1.读取并剔除无效数据 2.数据分组 3.提取最大值 4.提取最小值 三、总结 使用FME实现批量分组取每组数据的最大值和最小值,为类似场景的数据分析提取提供思路,例如提取宗地内建筑的最高层数等可参考此方法思路。关…...
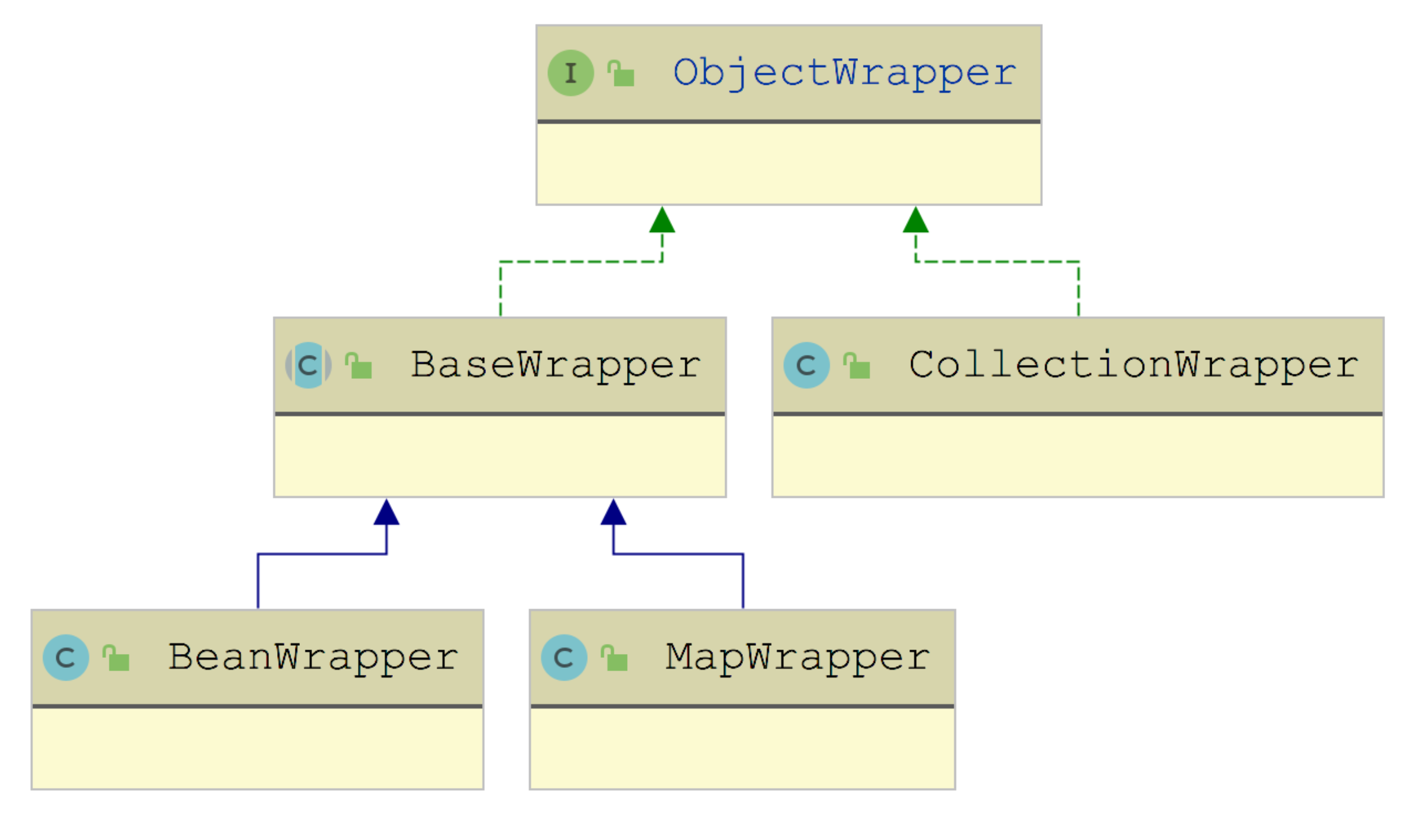
MyBatis 反射工具箱:带你领略不一样的反射设计思路
反射是 Java 世界中非常强大、非常灵活的一种机制。在面向对象的 Java 语言中,我们只能按照 public、private 等关键字的规范去访问一个 Java 对象的属性和方法,但反射机制可以让我们在运行时拿到任何 Java 对象的属性或方法。 有人说反射打破了类的封装…...
Netty第三部
继续Netty第二部的内容 一、ChannelHandler 1、ChannelHandler接口 ChannelHandler是Netty的主要组件,处理所有的入站和出站数据的应用程序逻辑的容器,可以应用在数据的格式转换、异常处理、数据报文统计等 继承ChannelHandler的两个子接口ÿ…...

【C++入门篇】保姆级教程篇【下】
目录 一、运算符重载 1)比较、赋值运算符重载 2) 流插入留提取运算符重载 二、剩下的默认成员函数 1)赋值运算符重载 2)const成员函数 3)取地址及const取地址操作符重载 三、再谈构造函数 1)初始化列表 …...

CCLink转Modbus TCP网关_CCLINK参数配置
CCLink转Modbus TCP网关(XD-ETHCL20),具有CCLINK主从站功能。主要用途是将各种MODBUS-TCP设备接入到CCLINK总线中。它可以作为从站连接到CCLINK总线上,也可以作为主站或从站连接到MODBUS-MTP总线上。 1、 配置网关的CCLINK参数&am…...
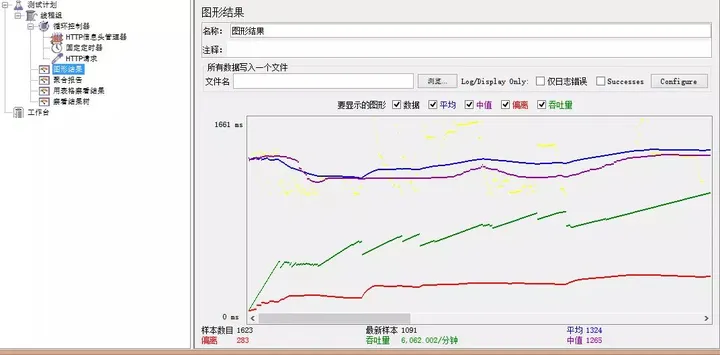
一文2000字从0到1使用压测神器JMeter进行压力测试!
概 述 Apache JMeter 是 Apache组织开发的基于 Java的压力测试工具。用于对软件做压力测试,它最初被设计用于 Web应用测试但后来扩展到其他测试领域。它可以用于测试静态和动态资源例如静态文件、Java 小服务程序、CGI 脚本、Java 对象、数据库, FTP 服…...

极狐GitLab CI 助力 .Net 项目研发效率和质量双提升
目录 .NET nuget 自动生成测试包(prerelease)版本号 .NET 版本号规范 持续集成自动打包 持续集成自动修改版本号 .NET 行级增量代码规范——拯救老项目 本地全量代码规范 行级增量代码规范 很多团队或开发者都会使用 C#、VB 等语言开发 .Net 应用…...
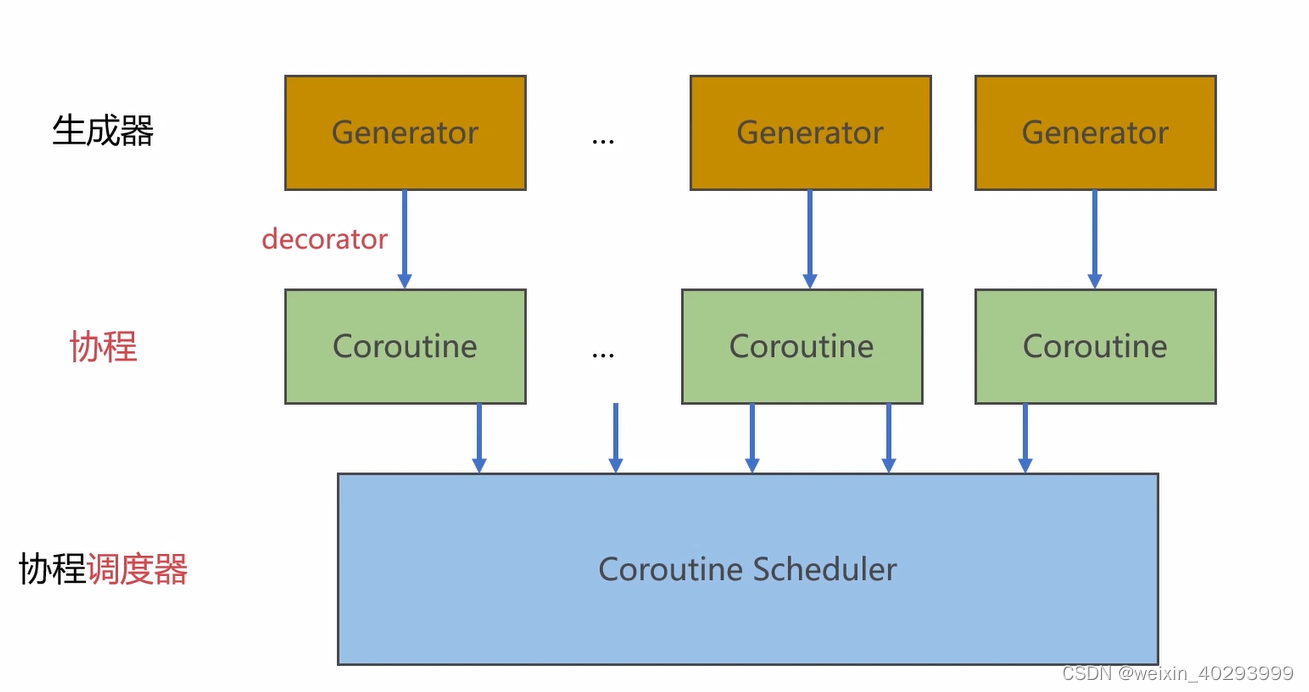
[协程]生成器协程调度器的实现-未完
本章内容的三个层次...
Git之分支与版本->课程目标及知识点的应用场景,分支的场景应用,标签的场景应用
1.课程目标及知识点的应用场景 Git分支和标签的命名规范 分支 dev/test/pre/pro(即master) dev:开发环境--windows (自己的电脑) test:测试环境--windows/linux (公司专门的测试电脑 pre:灰度环境(非常大的公司非常重要的项目) pro:正式环境 灰度环境与正式环境的服务器配置…...

PHP正则提取或替换img标记属性
<?php/*PHP正则提取图片img标记中的任意属性*/ $str <center><img src"/uploads/images/20100516000.jpg" height"120" width"120"><br />PHP正则提取或更改图片img标记中的任意属性</center>;//1、取整个图片代码…...

Git 命令行使用指南
Git 命令行使用指南 第一部分:配置 Git 1.1 设置用户信息1.2 配置换行符处理 第二部分:创建和配置仓库 2.1 初始化仓库2.2 克隆仓库2.3 递归克隆2.4 深度克隆 第三部分:基本操作 3.1 添加文件3.2 提交更改3.3 查看状态和提交历史3.4 创建和切…...

Spring 常见面试题
1、Spring概述 1.1、Spring是什么? Spring是一个轻量级Java开发框架,目的是为了解决企业级应用开发的业务逻辑层和其他各层的耦合问题Spring最根本的使命是解决企业级应用开发的复杂性,即简化Java开发。这些功能的底层都依赖于它的两个核心特性,也就是…...

caffe搭建squeezenet网络的整套工程
之前用pytorch构建了squeezenet,个人觉得pytorch是最好用的,但是有的工程就是需要caffe结构的,所以本篇也用caffe构建一个squeezenet网络。 数据处理 首先要对数据进行处理,跟pytorch不同,pytorch读取数据只需要给数据…...

【OWT】梳理构建的webrtc和owt mfc工程
梳理构建的webrtc和owt mfc工程M98 + owtp2p : 发现最终基于m98的owt也可以直接跑通 【owt】p2p client mfc 工程梳理 服务端使用github版本。 本地运行调试即可。 M98 VS2017 构建 :只构建了m98的webrtc.lib 【webrtc】vs2017 重新构建m98 G:\webrtc_m98_yjf\src webrtc本身…...

02 powershell服务器远程执行命令
一、获取服务器登录凭证 $Username myft\xngrq $PWD 123!# #将密码加密成特殊的字符串对象 $pass ConvertTo-SecureString -AsPlainText $PWD -Force #创建一个登录凭证对象 $Cred New-Object System.Management.Automation.PSCredential -ArgumentList $Username,$pass …...

LeetCode257. Binary Tree Paths
文章目录 一、题目二、题解 一、题目 Given the root of a binary tree, return all root-to-leaf paths in any order. A leaf is a node with no children. Example 1: Input: root [1,2,3,null,5] Output: [“1->2->5”,“1->3”] Example 2: Input: root […...
Linux下MSSQL (SQL Server)数据库无法启动故障处理
有同事反馈一套CentOS7下的mssql server2017无法启动需要我帮忙看看,启动报错情况如下 检查日志并没有更新日志信息 乍一看mssql-server服务有问题,检查mssql也确实没有进程 既然服务有问题,那么我们用一种方式直接手工后台启动mssql引擎来…...

2311极语言高亮说明书
入门 安装目录下Sec.exe为ide.Sc为编译器. .sec为单文件二进制源码结构,.SEC和.极为多文件文本结构,命令行:cmd Sc.exe 源码路径. 基础 整数变量也可以是万能指针,传送参数,参数只有整数和小数两种. 可在名称前面加或&符号取变量或函数名指针地址,文本变量只取地址不用加…...
金蝶云星空与金蝶云星空对接集成盘亏单查询打通盘亏单新增
金蝶云星空与金蝶云星空对接集成盘亏单查询打通盘亏单新增 接通系统:金蝶云星空 金蝶K/3Cloud(金蝶云星空)是移动互联网时代的新型ERP,是基于WEB2.0与云技术的新时代企业管理服务平台。金蝶K/3Cloud围绕着“生态、人人、体验”&am…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...