C++11 原始字符串字面量R“()“
原始字符串字面量(Raw String Literals)
R"()"是C++11引入的一项特性,它允许创建不需要转义字符的字符串字面量。字符串中包含特殊字符、换行符和其他转义字符时,不需要反斜杠转义它们。
-
原始(Raw):不用使用反斜杠转移某些字符,直接书写字符串的原始内容
-
字面量:程序中固定值的符号的一种表示,通常是表示常量的一种方式。常见字面量
- 整数字面量:42
- 浮点数字面量:3.14
- 字符字面量:‘A’
- 字符串字面量:“Hello, World!”
- 布尔字面量:true 或 false
- 空指针字面量:nullptr(C++11及以后版本)
比如,在LearnOpenGL CN中,表示一段shader代码,并未使用原始字符串字面量 ,就需要把所有换行符手动写出,如:
const char* glslCode ="#version 330 core\n""\n""layout(location = 0) in vec3 inPos;\n""layout(location = 1) in vec3 inCol;\n""\n""out vec3 fragColor;\n""\n""void main() {\n"" fragColor = inCol;\n""}\n";
如果使用原始字符串字面量:优雅
const char* glslCode = R"(#version 330 corelayout(location = 0) in vec3 inPosition;layout(location = 1) in vec3 inColor;out vec3 fragColor;void main() {fragColor = inColor;})";
相关文章:
“)
C++11 原始字符串字面量R“()“
原始字符串字面量(Raw String Literals) R"()"是C11引入的一项特性,它允许创建不需要转义字符的字符串字面量。字符串中包含特殊字符、换行符和其他转义字符时,不需要反斜杠转义它们。 原始(Raw):不用使用反…...

【Vue原理解析】之虚拟DOM
Vue.js是一款流行的JavaScript框架,它采用了虚拟DOM(Virtual DOM)的概念来提高性能和开发效率。虚拟DOM是Vue.js的核心之一,它通过在内存中构建一个轻量级的DOM树来代替直接操作真实的DOM,从而减少了对真实DOM的操作次…...
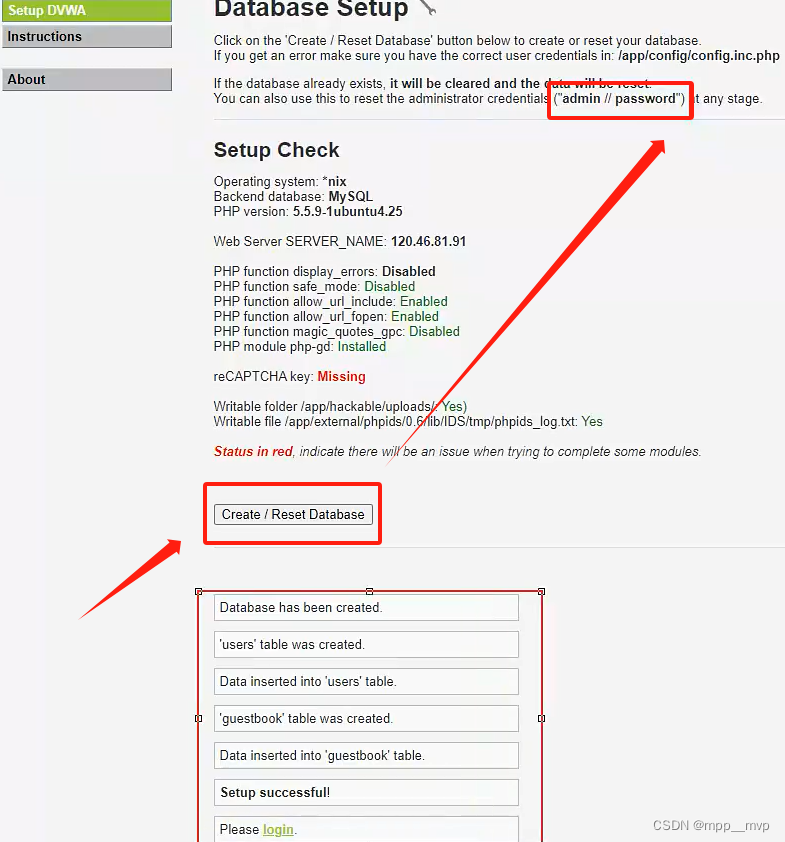
HCIE-灾备技术和安全服务
灾备技术 灾备包含两个概念:容灾、备份 备份是为了保证数据的完整性,数据不丢失。全量备份、增量备份,备份数据还原。 容灾是为了保证业务的连续性,尽可能不断业务。 快照:保存的不是底层块数据,保存的是逻…...

【图论实战】Boost学习 01:基本操作
文章目录 头文件图的构建图的可视化基本操作 头文件 #include <boost/graph/adjacency_list.hpp> #include <boost/graph/graphviz.hpp> #include <boost/graph/properties.hpp> #include <boost/property_map/property_map.hpp> #include <boost/…...
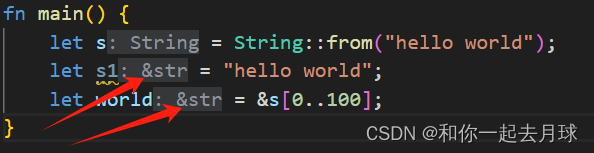
Rust 中的引用与借用
目录 1、引用与借用 1.1 可变引用 1.2 悬垂引用 1.3 引用的规则 2、slice 类型 2.1 字符串字面量其实就是一个slice 2.2 总结 1、引用与借用 在之前我们将String 类型的值返回给调用函数,这样会导致这个String会被移动到函数中,这样在原来的作用域…...
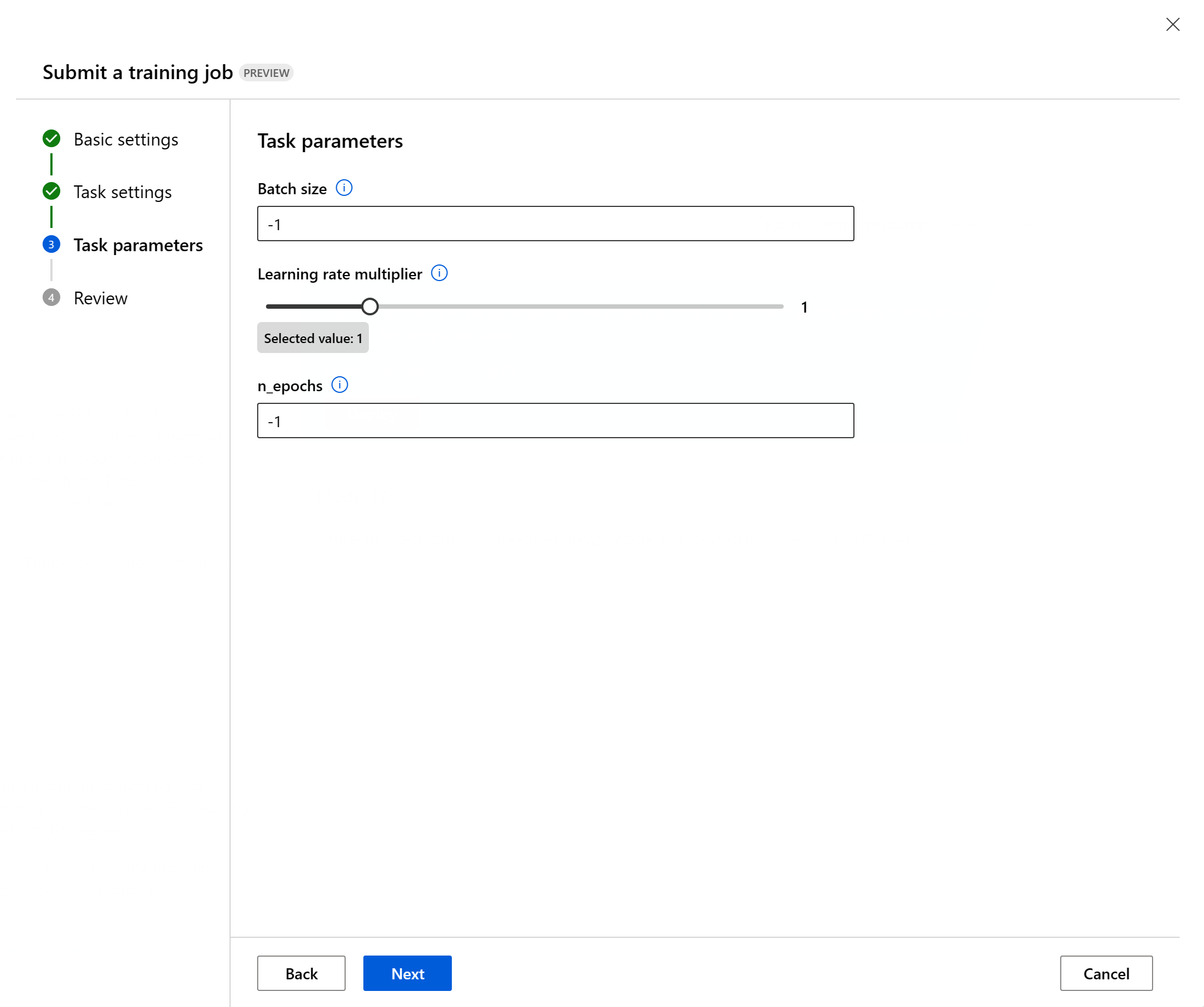
Azure 机器学习:在 Azure 机器学习中使用 Azure OpenAI 模型
目录 一、环境准备二、Azure 机器学习中的 OpenAI 模型是什么?三、在机器学习中访问 Azure OpenAI 模型连接到 Azure OpenAI部署 Azure OpenAI 模型 四、使用自己的训练数据微调 Azure OpenAI 模型使用工作室微调微调设置训练数据自定义微调参数部署微调的模型 使用…...
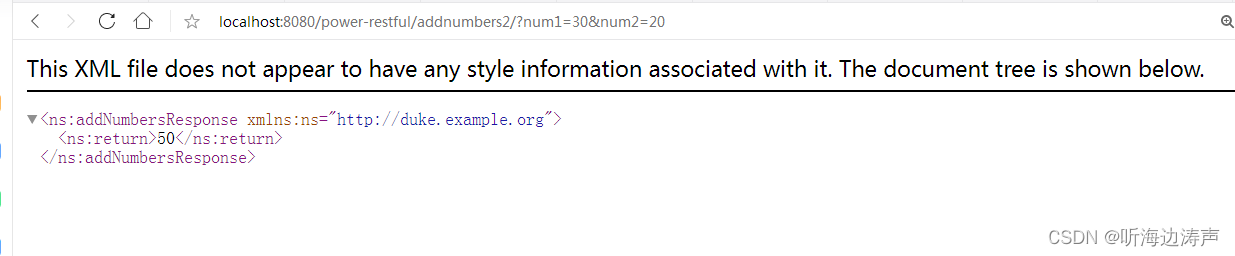
XML Web 服务 Eclipse实现中的sun-jaxws.xml文件
说明 在sun-jaxws.xml文件,可以配置endpoint、handler-chain等内容。在这个文件中配置的内容会覆盖在Java代码中使用注解属性配置的的内容。 这个文件根据自己的项目内容修改完成以后,作为web应用的一部分部署到web容器中(放到web应用的WEB…...

16.1 二次根式 教学设计及课堂检测设计
课堂检测如下:...

Android数据流的狂欢:Channel与Flow
在 Android 应用程序的开发中,处理异步数据流是一个常见的需求。为了更好地应对这些需求,Kotlin 协程引入了 Channel 和 Flow,它们提供了强大的工具来处理数据流,实现生产者-消费者模式,以及构建响应式应用程序。 本文…...

Java 单元测试最佳实践:如何充分利用测试自动化
单元测试是众所周知的做法,但还有很大的改进空间!在这篇文章中,我们讨论最有效的单元测试最佳实践,包括在此过程中最大化自动化工具的方法。我们还将讨论代码覆盖率、模拟依赖关系和整体测试策略。 什么是单元测试? 单…...
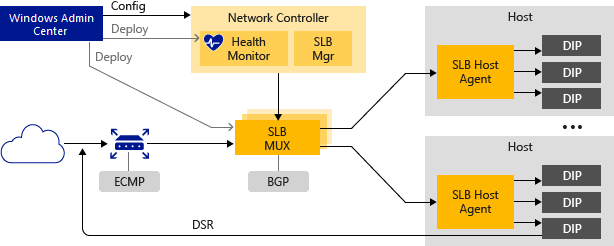
windows系统用于 SDN 的软件负载均衡器 (SLB)
适用于:Azure Stack HCI 版本 22H2 和 21H2;Windows Server 2022、Windows Server 2019、Windows Server 2016 软件负载均衡器包括哪些内容? 软件负载均衡器提供以下功能: 适用于北/南和东/西 TCP/UDP 流量的第 4 层 (L4) 负载均…...
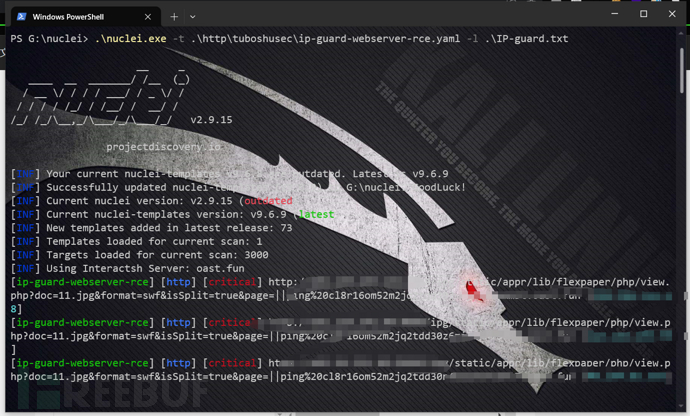
漏洞复现--IP-guard flexpaper RCE
免责声明: 文章中涉及的漏洞均已修复,敏感信息均已做打码处理,文章仅做经验分享用途,切勿当真,未授权的攻击属于非法行为!文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直…...
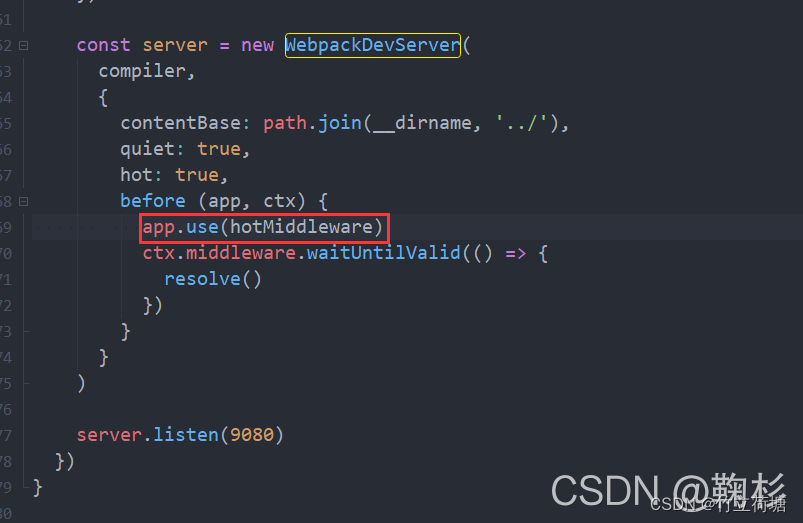
Electron-vue出现GET http://localhost:9080/__webpack_hmr net::ERR_ABORTED解决方案
GET http://localhost:9080/__webpack_hmr net::ERR_ABORTED解决方案 使用版本解决方案解决总结 使用版本 以下是我解决此问题时使用的electron和vue等的一些版本信息 【附】经过测试 electron 的版本为 13.1.4 时也能解决 解决方案 将项目下的 .electron-vue/dev-runner.js…...

Linux---(六)自动化构建工具 make/Makefile
文章目录 一、make/Makefile二、快速查看(1)建立Makefile文件(2)编辑Makefile文件(3)解释(4)效果展示 三、背后的基本知识、原理(1)如何清理对应的临时文件呢…...

谷歌:编写干净的代码以减少认知负荷
您是否曾经阅读过代码却发现很难理解?您可能正在经历认知负荷! 认知负荷是指完成一项任务所需的脑力劳动量。阅读代码时,您必须记住变量值、条件逻辑、循环索引、数据结构状态和接口契约等信息。随着代码变得更加复杂,认知负荷也…...
微信小程序display常用属性和子元素排列方式介绍
wxss中display常用显示属性与css一致,介绍如下: 针对元素本身显示的属性: displayblock,元素显示换行displayinline,元素显示换行,但不可设置固定的宽度和高度,也不可设置上下方向的margin和p…...

设计模式—结构型模式之代理模式
设计模式—结构型模式之代理模式 代理模式(Proxy Pattern) ,给某一个对象提供一个代理,并由代理对象控制对原对象的引用,对象结构型模式。 静态代理 比如我们有一个直播平台,提供了直播功能,但是如果不进行美颜,可能就比较冷清…...

C# PDF转HTML字符串
需要nuget安装Aspose.PDF插件,本文使用23.10.0版本 一、获取PDF文件,保存到某个路径;再读取返回字符串。 //html文件保存路径 string filePath dirPath "xxx.html"; if (!File.Exists(filePath)) {//获取pdf文件流Byte[] pdfBy…...
el-table解决数据过少小于高度有留白的问题
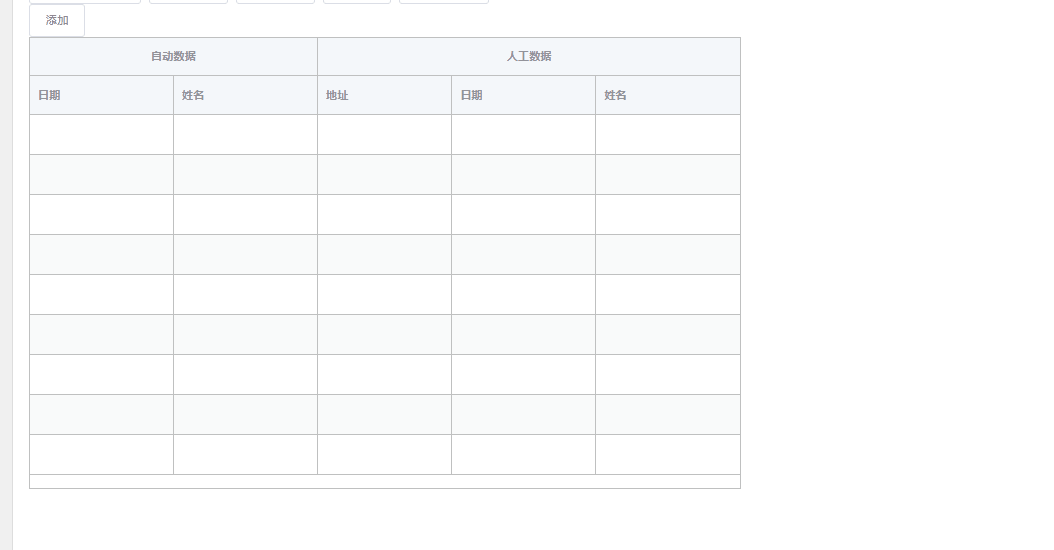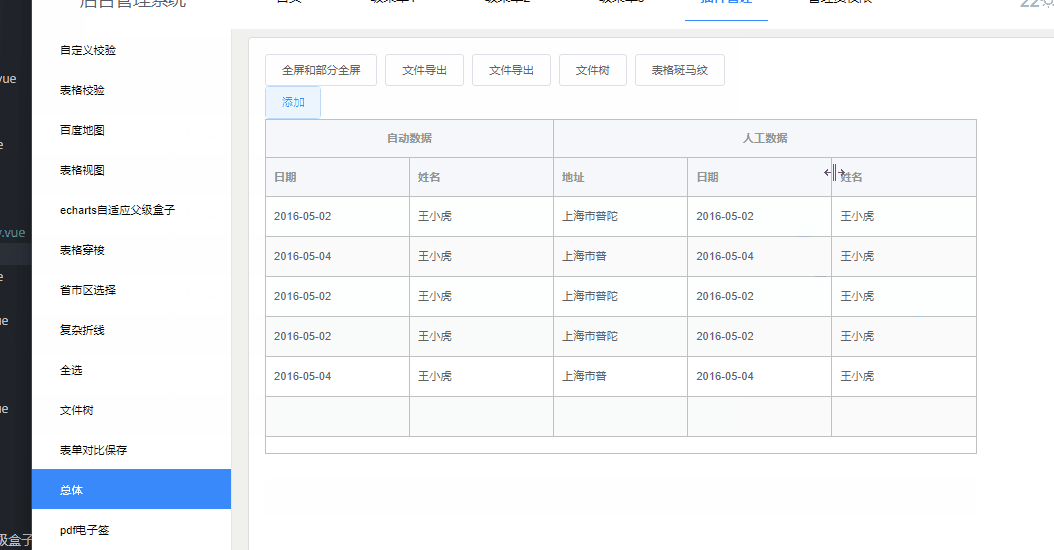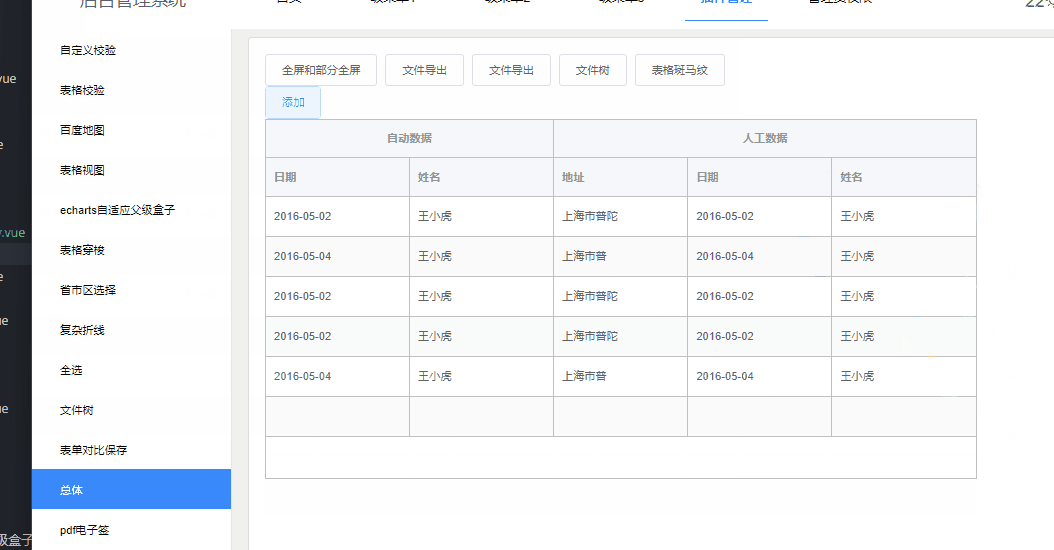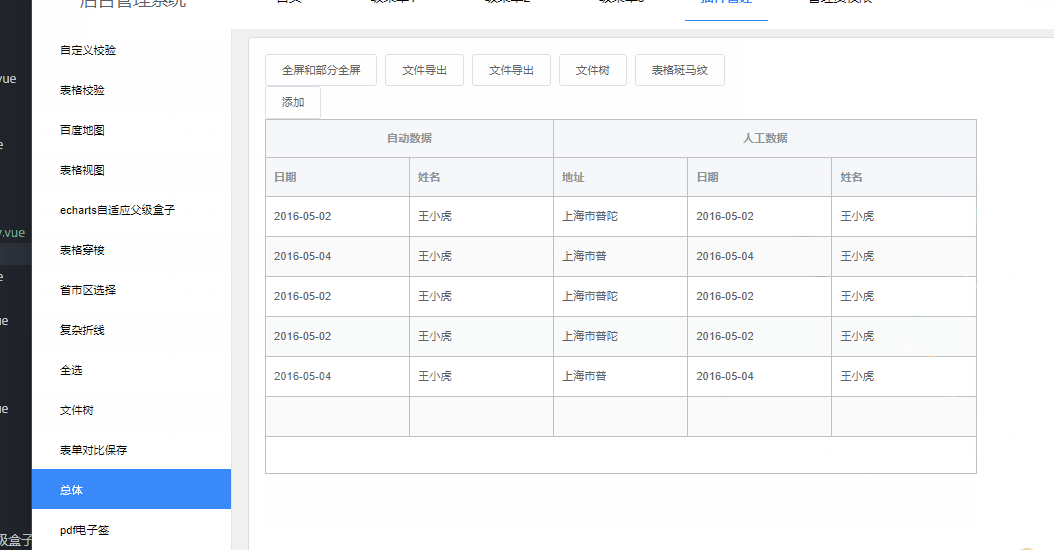
问题:给el-table设置个高度,高度为500px,之后就添加如下4条数据,那么底部就没数据,直接就空白了,本文章就是为了解决这个问题,如果底部留白那么就添加几条空数据就行了.如果数据已达到高度了那么就不会留白了 1.效果 这个空列可以根据高度来决定添加几个空格子去铺满列表&…...

vue实现无感刷新token
vue实现无感刷新token 1、前言2、实现思路2.1 方法一2.2 方法二2.3 方法三 3、可能遇到的问题3.1 问题一:如何防止多次刷新token3.2 问题二:同时发起两个或者两个以上的请求时,其他接口怎么解决 1、前言 最近在做vue3管理系统项目的时候&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
