leetcode刷题日记:121. Best Time to Buy and Sell Stock( 买卖股票的最佳时机)
题目给了我们一组数prices,其中prices[i]表示第i天的股票价格,需要我们求出买卖股票所能获得的最大收益。
我们的第一想法就是从算出每一种买卖股票的情况然后求出里面的最大值,这样我们就能得到最大收益是多少,但是这种情况过于复杂他需要考虑前一天和后面所有天的情况,这无疑是复杂的,因为我们可以大致算出时间复杂度是 O ( n 3 ) O(n^3) O(n3),这在问题规模较小时还可以接受一旦问题规模上升,所需要的时间也快速上升,我们需要找到一种更加快速的算法。
上面思路的代码。
int maxProfit(int* prices, int pricesSize) {int profit = 0;for(int i=0; i<pricesSize; i++){for(int j=i+1; j<pricesSize; j++){int x = prices[j]-prices[i];if(x>profit){profit = x; }}}return profit;
}
我们想一下我们可以从哪些情况去进行优化呢?刚才我们想的是从前向后找,但是我们知道第i天的最大利润等于第i天的价钱减前i-1天中的最小值,我们这样的话求某一天的利润就不需要看很多情况只需要看一下前n-1天的最小值,这样的话时间复杂度就大大减小了,我们只需要更新前n-1天最小值就行了。
int maxProfit(int *prices, int pricesSize){int min = prices[0];int profit = 0;for(int i=1;i<pricesSize;i++){if(prices[i]<=min){min = prices[i];}else if(prices[i]-min>profit){profit = prices[i]-min;}}return profit;
}
运行结果截图:
上面这两种算法时间的差异主要在于第一种算法假定的是当前检查的是最小的,然后向后寻找可能比他大的,后面的都是未检查的,所以要每一种情况都检查,第二种算法是认为已经检查过的是最小的,当前检查的是最大的,我们对于最小元素的信息已知,不需要检查别的情况,在检查的过程种遇到比其更小的就更新最小的值,所以情况少时间效率高。
相关文章:

leetcode刷题日记:121. Best Time to Buy and Sell Stock( 买卖股票的最佳时机)
题目给了我们一组数prices,其中prices[i]表示第i天的股票价格,需要我们求出买卖股票所能获得的最大收益。 我们的第一想法就是从算出每一种买卖股票的情况然后求出里面的最大值,这样我们就能得到最大收益是多少,但是这种情况过于复…...
Mac 本地部署thinkphp8【部署环境以及下载thinkphp】
PHP的安装以及环境变量配置 1 PHP安装:在终端输入brew install php 这里是PHP下载的最新的 如果提示‘brew’找不到,自己搜索安装吧, 不是特别难 2 环境变量配置 终端输入vim ~/.bash_profile 输入export PATH"/usr/local/Cellar/php/8.…...
【汽车电子】CAN总线分析仪使用介绍(PCAN/同星CAN卡)
本篇文章以CAN卡的使用为基本线索,介绍了在汽车电子领域涉及的一些CAN卡使用流程,搭配强大的上位机可以实现诸多功能。文章并没有局限于一种CAN卡,而是针对PCAN和同星的CAN卡分别以常用CAN报文收发以及诊断控制台实现这两种方向进行了CAN卡使…...

C //例 7.13 有一个3*4的矩阵,求所有元素中的最大值。
C程序设计 (第四版) 谭浩强 例 7.13 例 7.13 有一个3*4的矩阵,求所有元素中的最大值。 IDE工具:VS2010 Note: 使用不同的IDE工具可能有部分差异。 代码块 方法:使用指针、动态分配内存 #include <stdio.h> …...
基于SSM的供电所档案管理系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...
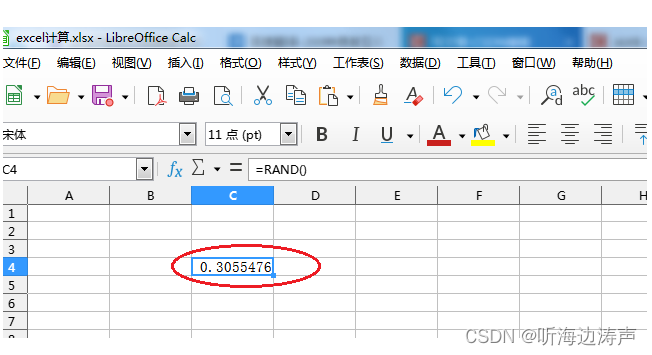
excel用RAND函数生成一个大于0小于1的随机数
插入-》函数: 选择RAND函数: 点击“继续”: 点击“确定”,就生成随机数了:...
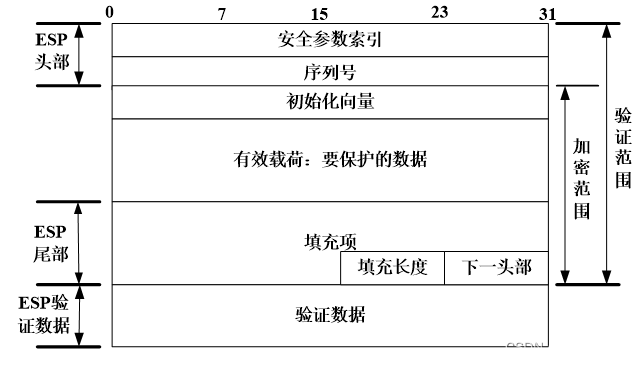
详解IP安全:IPSec协议簇 | AH协议 | ESP协议 | IKE协议
目录 IP安全概述 IPSec协议簇 IPSec的实现方式 AH(Authentication Header,认证头) ESP(Encapsulating Security Payload,封装安全载荷) IKE(Internet Key Exchange,因特网密钥…...

mysql使用--数据库的基本操作
在MYSQL中,一些表的集合称为一个数据库。MYSQL服务器管理若干个数据库,每个数据库下都可有若干个表。 1.展示数据库 SHOW DATABASES; 2.创建数据库 如:CREATE DATABASE myname; 更智能语法,可用:CREATE DATABASE IF …...

计算机毕业设计选题推荐-个人记账理财微信小程序/安卓APP-项目实战
✨作者主页:IT毕设梦工厂✨ 个人简介:曾从事计算机专业培训教学,擅长Java、Python、微信小程序、Golang、安卓Android等项目实战。接项目定制开发、代码讲解、答辩教学、文档编写、降重等。 ☑文末获取源码☑ 精彩专栏推荐⬇⬇⬇ Java项目 Py…...

如何利用IP代理进行海外推广?
在当今数字化的时代,网络营销已经成为企业策略的重要组成部分。而对于进去海外市场的跨境玩家来说,海外的推广推广是重中之重。然而,在开展推广的过程中,我们常常会遇到各种挑战,如地域限制、访问速度慢等。 为了解决…...
流)
使用FFmpeg转封装为hls(m3u8)流
改造ffmpeg/doc/examples/remuxing.c,支持将输入流转封装为hls协议对应的github地址:GitHub - yagerfgcs/FFmpeg at examples/remuxing_support_hls修改点:增加设置hls头 // example:https://www.ffmpeg.org/ffmpeg-all.html#hls-2 // f…...
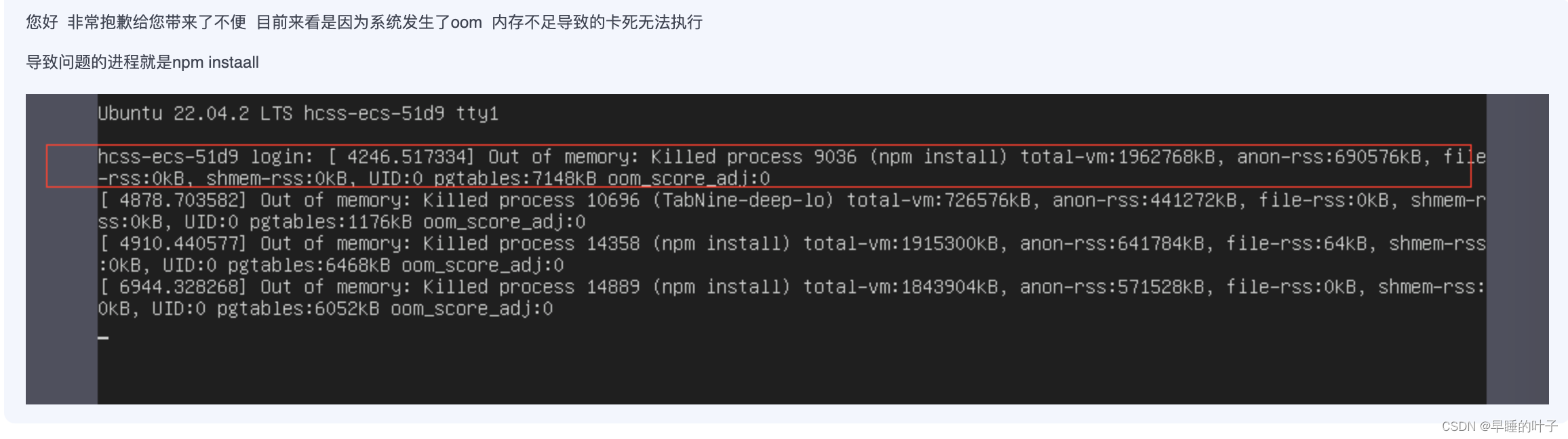
npm install导致的OOM解决方案
文章目录 问题记录解决方法Linux重启排查方法 如何排查Linux自动重启的原因 问题记录 我在华为云服务器配置npm开发环境的时候, SSH远程连接一直掉线,无奈提了工单,被告知是NPM install导致的OOM问题。无语了,破NPM还有这个问题呢…...
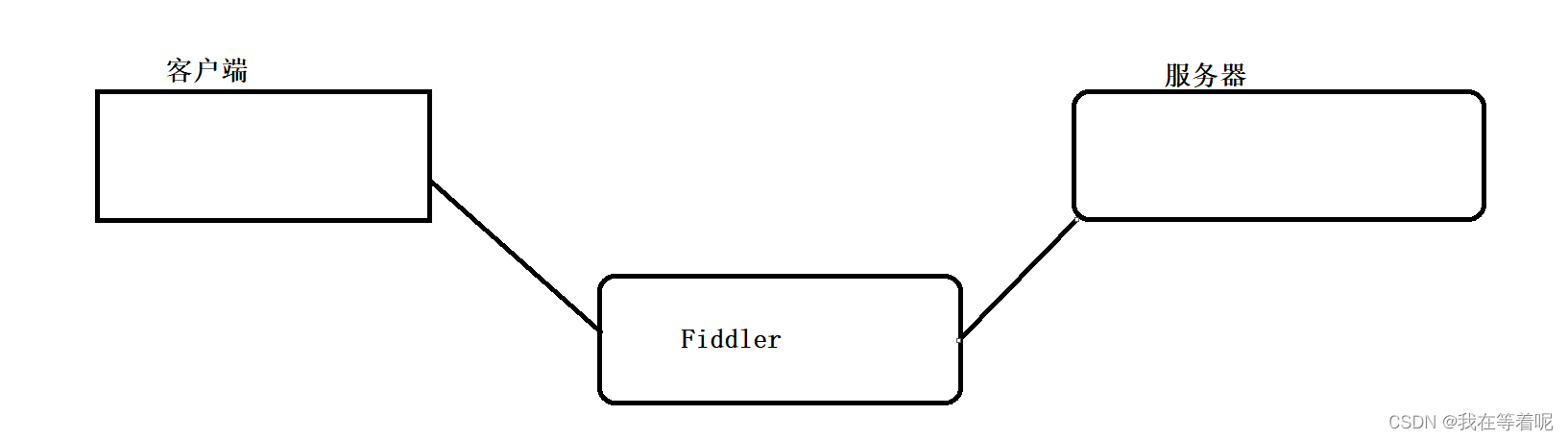
HTTP和HTTPS详解
一)什么是HTTP协议 1)HTTP协议是倾向于相遇业务层次上面的一种协议,传输层协议主要考虑的是端对端之间的一个传输过程,TCP重点进行关注的是可靠传输;咱们的HTTP/1,HTTP/2是基于TCP的,但是咱们的HTTP/3是基于UDP的&…...
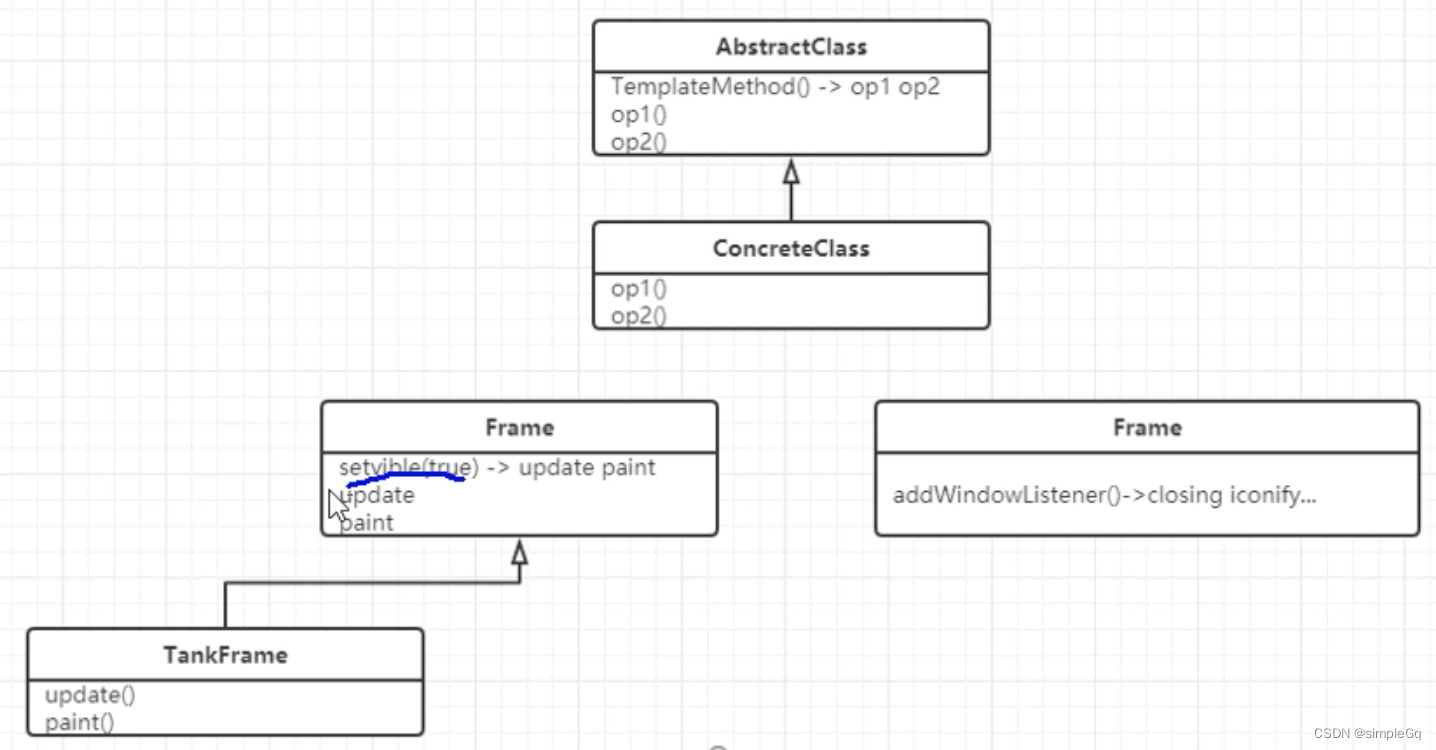
设计模式之模版方法(TemplateMethod)
模版方法 钩子函数 回调函数 在父类里面有一个模版方法,在这个方法里面调用了op1,op2,op3… 在子类里面如果想要改变父类的op1和op2 只需要重写op1和op2,那么这个重写之后的方法,可以在父类里面直接调用的到 例子: J…...

为什么数据安全很重要?哪些措施保护数据安全?
数据安全很重要的原因是因为数据是现代社会的重要财产之一。很多组织和企业依赖数据来做出商业决策,管理客户关系,进行财务规划等等。如果这些数据泄露或遭到黑客攻击,那么就会影响企业的经济利益,甚至影响到个人的隐私和安全。此…...

git push 操作代码回退
git reset revert 回退回滚取消提交返回上一版本 总有一天你会遇到下面的问题. (1)改完代码匆忙提交,上线发现有问题,怎么办? 赶紧回滚. (2)改完代码测试也没有问题,但是上线发现你的修改影响了之前运行正常的代码报错,必须回滚. 这些开发中很常见的问题,所以git的取消提交…...
ESP32 Arduino引脚分配参考:您应该使用哪些 GPIO 引脚?
ESP32 芯片有 48 个引脚,具有多种功能。并非所有 ESP32 开发板中的所有引脚都暴露出来,有些引脚无法使用。 关于如何使用 ESP32 GPIO 有很多问题。您应该使用什么引脚?您应该避免在项目中使用哪些引脚?这篇文章旨在成为 ESP32 GP…...

【链接装载与库】 Linux共享库的组织
Linux共享库的组织 由于动态链接的诸多优点,大量的程序开始使用动态链接机制,导致系统里面存在数量 极为庞大的共享对象。如果没有很好的方法将这些共享对象组织起来,整个系统中的共享对象文件则会散落在各个目录下,给长期的维护…...
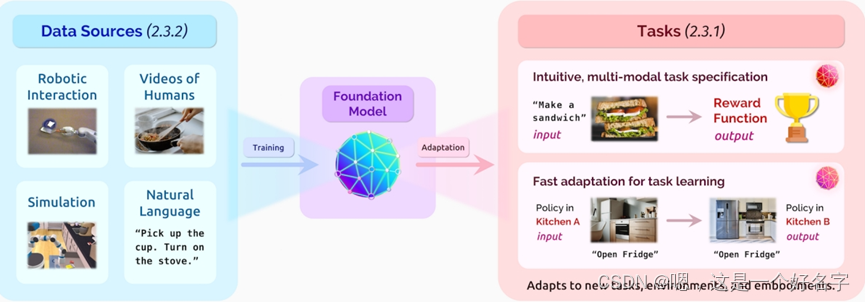
大模型时代的机器人研究
机器人研究的一个长期目标是开发能够在物理上不同的环境中执行无数任务的“多面手”机器人。对语言和视觉领域而言,大量的原始数据可以训练这些模型,而且有虚拟应用程序可用于应用这些模型。与上述两个领域不同,机器人技术由于被锚定在物理世…...

devops步骤 -- jenkins安装
安装的docker-compose ##安装步骤参考: https://editor.csdn.net/md/?articleId133070011 编写docker-compose.yml version: 3 services: # 集合docker_jenkins:user: root # 为了避免一些…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
