【代码训练营】day44 | 完全背包理论 518. 零钱兑换 II 377. 组合总和 Ⅳ
所用代码 java
完全背包
01背包物品只能使用一次 – 倒序遍历
for(i = 0; i < weight.length; i++){ 物品for (j = bagWeight; j >= weight[i]; j--){ 背包dp[j] = max(dp[j], dp[j-weight[i]] + value[i])}
}
完全背包物品可以使用无限次 – 正序遍历
for(i = 0; i < weight.length; i++){ 物品for (j = weight[i]; j <= bagWeight; j++){ 背包dp[j] = max(dp[j], dp[j-weight[i]] + value[i])}
}
完全背包for循环中可以颠倒,先遍历谁都可以
零钱兑换 II LeetCode 518
题目链接:零钱兑换 II LeetCode 518 - 中等
思路
-
dp[j]:装满背包j的情况有dp[j]种
-
递推公式:dp[j] += dp[j-coins[i]]
-
初始化:dp[0] = 1 如果等于0,后面累加就会一直是0, 空集也是一种方法
- dp[1] += dp[0],1要从0得到结果然后继续累加
-
遍历方向:coins[i] <= j <= amount
-
打印dp
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount + 1];dp[0] = 1;for (int i = 0; i < coins.length; i++) { // 物品for (int j = coins[i]; j <= amount; j++){ // 背包dp[j] += dp[j-coins[i]];
// System.out.print("\tdp[j] = " + dp[j]);}
// System.out.println();}return dp[amount];}
}
总结
先遍历物品,后遍历背包,保证了物品是从1、2、3开始的,不会有重复,也就是说这是一个组合数。
若先遍历背包,再遍历物品,每次物品都是从1开始,就会有重复数,如1,2 2,1 但是这可以代表排列数。
组合总和 Ⅳ leetCode 377
题目链接:组合总和 Ⅳ leetCode 377 - 中等
思路
- dp[j] :和为j的情况有dp[j]种
- 递推:dp[j] += dp[j-nums[i]]
- 初始化:dp[0] = 1
- 遍历顺序:先背包,后物品
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int j = 0; j <= target; j++) { // 背包for (int i = 0; i < nums.length; i++) { // 物品if (j >= nums[i]) dp[j] += dp[j-nums[i]];System.out.print("\tdp[j] = " +dp[j]);}System.out.println();}return dp[target];}
}
总结
背包为0可以装下物品 1 2 3 这其实是一个悖论,也可以认为是背包为0的可以装下无限大的东西。但是我认为把这个看成一个初始化无意义的值就行了,以防止出现后序累加的值一直为0。
dp数组的打印值
dp[j] = 1 dp[j] = 1 dp[j] = 1dp[j] = 1 dp[j] = 1 dp[j] = 1dp[j] = 1 dp[j] = 2 dp[j] = 2dp[j] = 2 dp[j] = 3 dp[j] = 4dp[j] = 4 dp[j] = 6 dp[j] = 7
若是觉得这值确实没必要,我们其实可以从j=1开始遍历,所打印的值就有助于对于dp数组的理解。
dp[j] = 1 dp[j] = 1 dp[j] = 1dp[j] = 1 dp[j] = 2 dp[j] = 2dp[j] = 2 dp[j] = 3 dp[j] = 4dp[j] = 4 dp[j] = 6 dp[j] = 7
所以,通过这两个题,我们可以明白:
- 先遍历物品,再遍历背包:组合问题 - 无重复
- 先遍历背包,再遍历物品:排列数 - 有重复(可排序)
相关文章:

【代码训练营】day44 | 完全背包理论 518. 零钱兑换 II 377. 组合总和 Ⅳ
所用代码 java 完全背包 01背包物品只能使用一次 – 倒序遍历 for(i 0; i < weight.length; i){ 物品for (j bagWeight; j > weight[i]; j--){ 背包dp[j] max(dp[j], dp[j-weight[i]] value[i])} }完全背包物品可以使用无限次 – 正序遍历 for(i 0; i < weigh…...
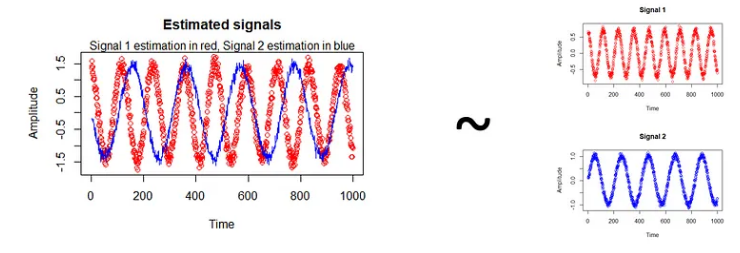
ICA简介:独立成分分析
1. 简介 您是否曾经遇到过这样一种情况:您试图分析一个复杂且高度相关的数据集,却对信息量感到不知所措?这就是独立成分分析 (ICA) 的用武之地。ICA 是数据分析领域的一项强大技术,可让您分离和识别多元数据集中的底层独立来源。 …...

②【Java 组】蓝桥杯省赛真题解析 [振兴中华] [三部排序] 持续更新中...
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 蓝桥杯真题--持续更新中...一、振兴中华二、三…...

PostgreSql 视图
一、概述 视图(View)本质上是一个存储在数据库中的查询语句。视图本身不包含数据,也被称为虚拟表。 我们在创建视图时给它指定了一个名称,然后可以像表一样对其进行查询。 优势: 不保存数据,节省空间。减少…...
)
【PAT甲级题解记录】1150 Travelling Salesman Problem (25 分)
【PAT甲级题解记录】1150 Travelling Salesman Problem (25 分) 前言 Problem:1150 Travelling Salesman Problem (25 分) Tags:模拟 图的遍历 旅行商问题 Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1150 Travell…...
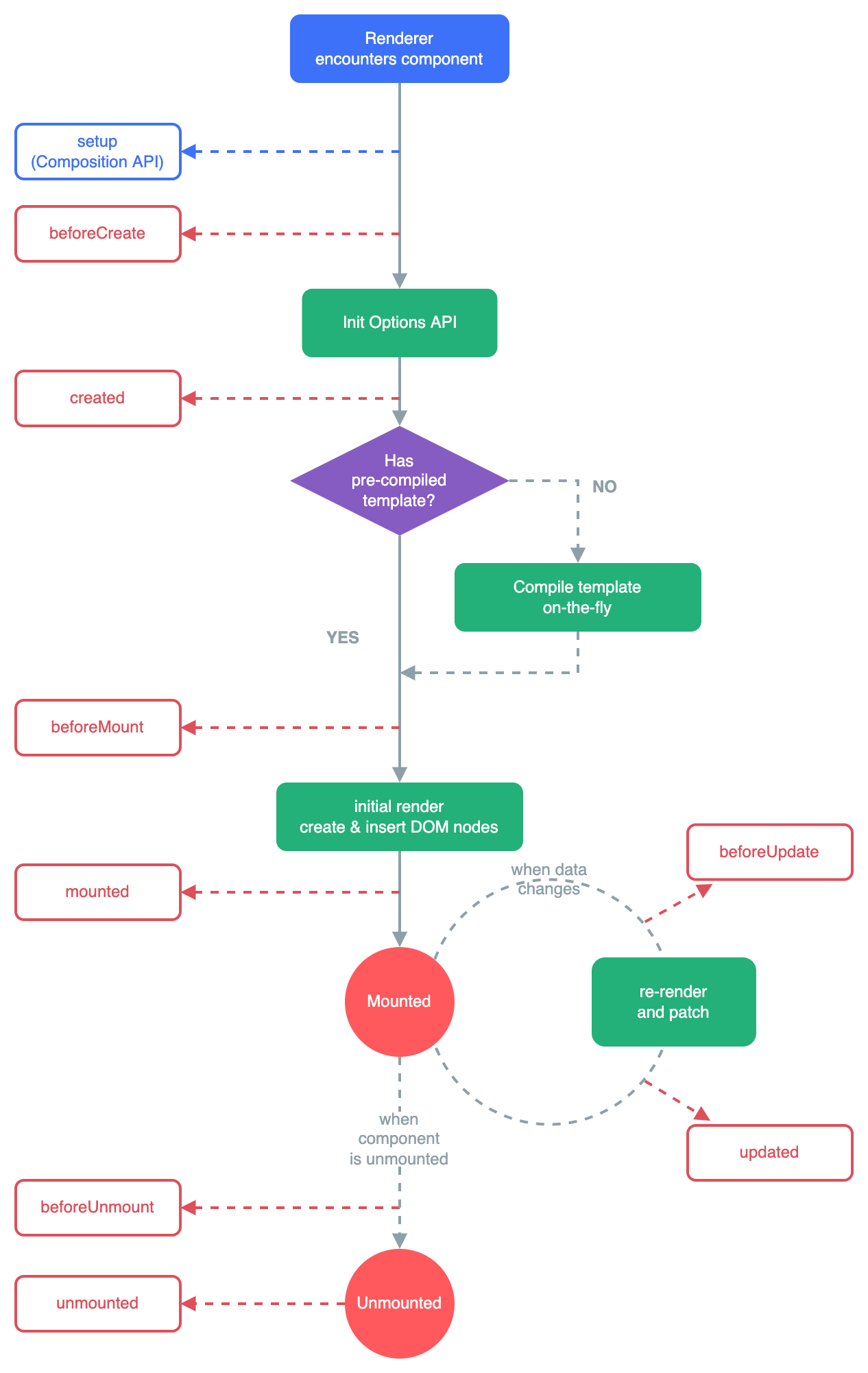
vue生命周期
vue生命周期是什么?Vue生命周期是指vue实例对象从创建之初到销毁的过程,vue所有功能的实现都是围绕其生命周期进行的,在生命周期的不同阶段调用对应的钩子函数可以实现组件数据管理和DOM渲染两大重要功能。我们来看一下官网给的vue生命周期的…...

排查解决Java进程占用内存过高
排查解决Java进程占用内存过高1 在项目部署运行之前1 检查JVM参数设置2 检查代码逻辑3 使用内存分析工具4 检查线程5 调整应用程序的设计7 调整硬件资源2 在项目部署运行之后1 在项目部署运行之前 1 检查JVM参数设置 检查JVM的启动参数设置,包括-Xmx和-Xms参数&am…...
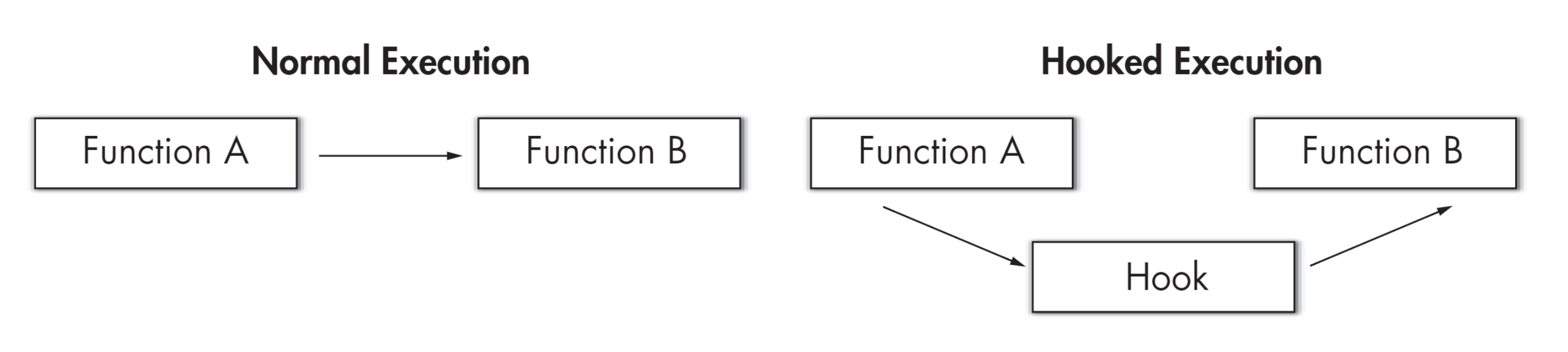
一个基于 LKM 的 Linux 内核级 rootkit 的实现
博客已迁移至:https://gls.show/ GitHub链接 演示Slides overview rootkit是一种恶意软件,攻击者可以在获得 root 或管理员权限后安装它,从而隐藏入侵并保持root权限访问。rootkit可以是用户级的,也可以是内核级的。关于rootk…...

CAN工具 - ValueCAN - 基础介绍(续)
VSpy3(Vehicle Spy 3的简写),作为一个常用的车载总线仿真工具,在车载网络领域也是有非常大的市场,前面也简单介绍过一些简单的功能,今天就再次介绍一些。什么是VSpy3?VSpy3是美国英特佩斯公司下…...
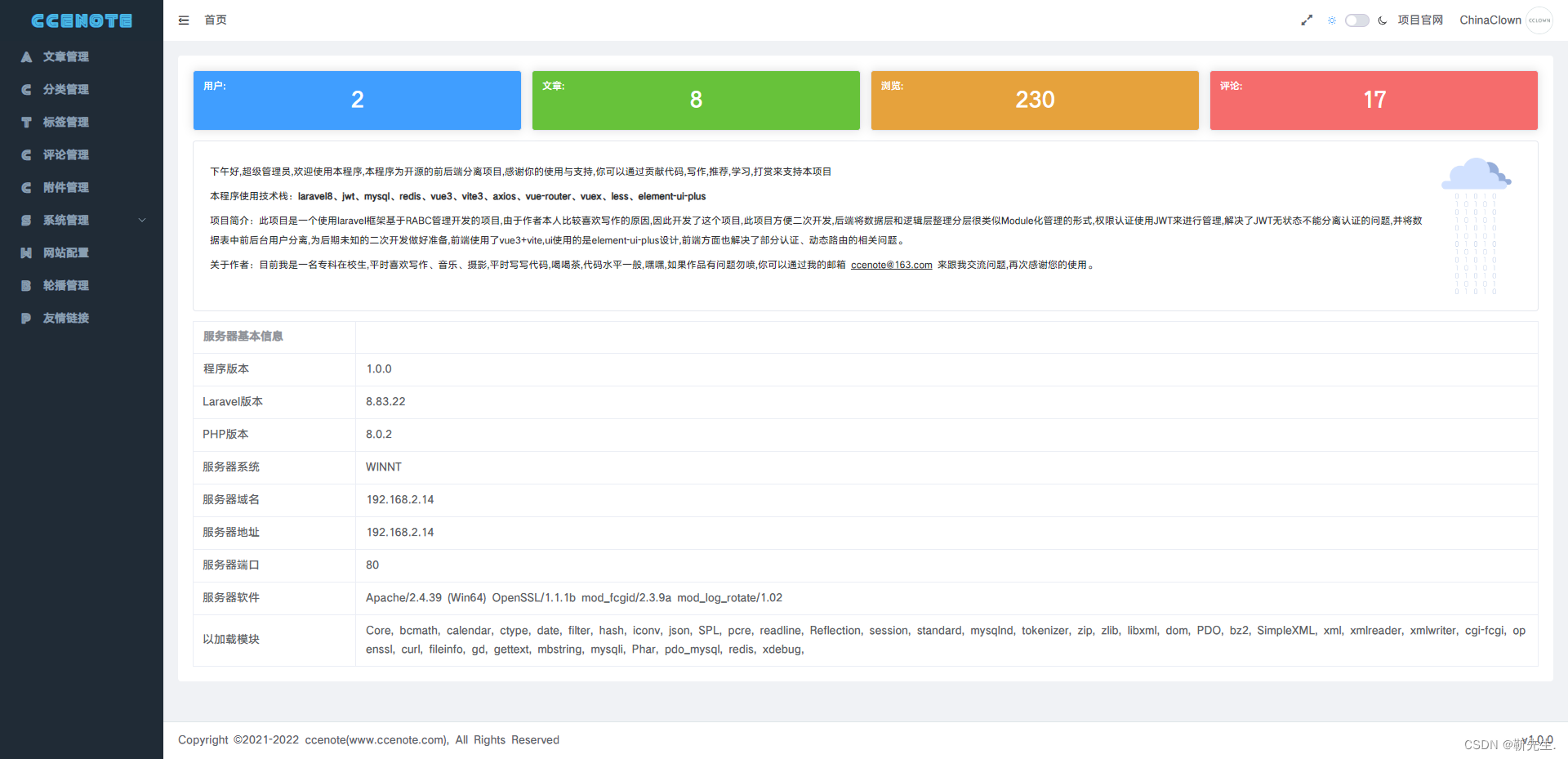
一个Laravel+vue免费开源的基于RABC控制的博客系统
项目介绍 CCENOTE 是一个使用 Vue3 Laravel8 开发的前后端分离的基于RABC权限控制管理的内容管理系统,由于作者本人比较喜欢写作的原因,因此开发了这个项目,后端使用的PHP的Laravel框架,并且整理了数据层与业务层,相…...
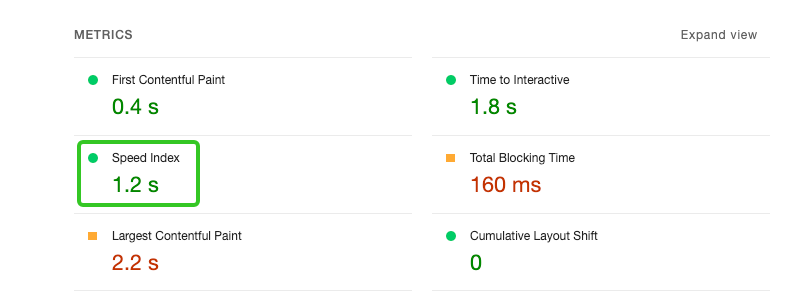
从 B 站出发,用 Chrome devTools performance 分析页面如何渲染
页面是如何渲染的?通常会得到“解析 HTML、css 合成 Render Tree,就可以渲染了”的回答。但是具体都做了些什么,却很少有人细说,我们今天就从 Chrome 的性能工具开始,具体看看一个页面是如何进行渲染的,以及…...
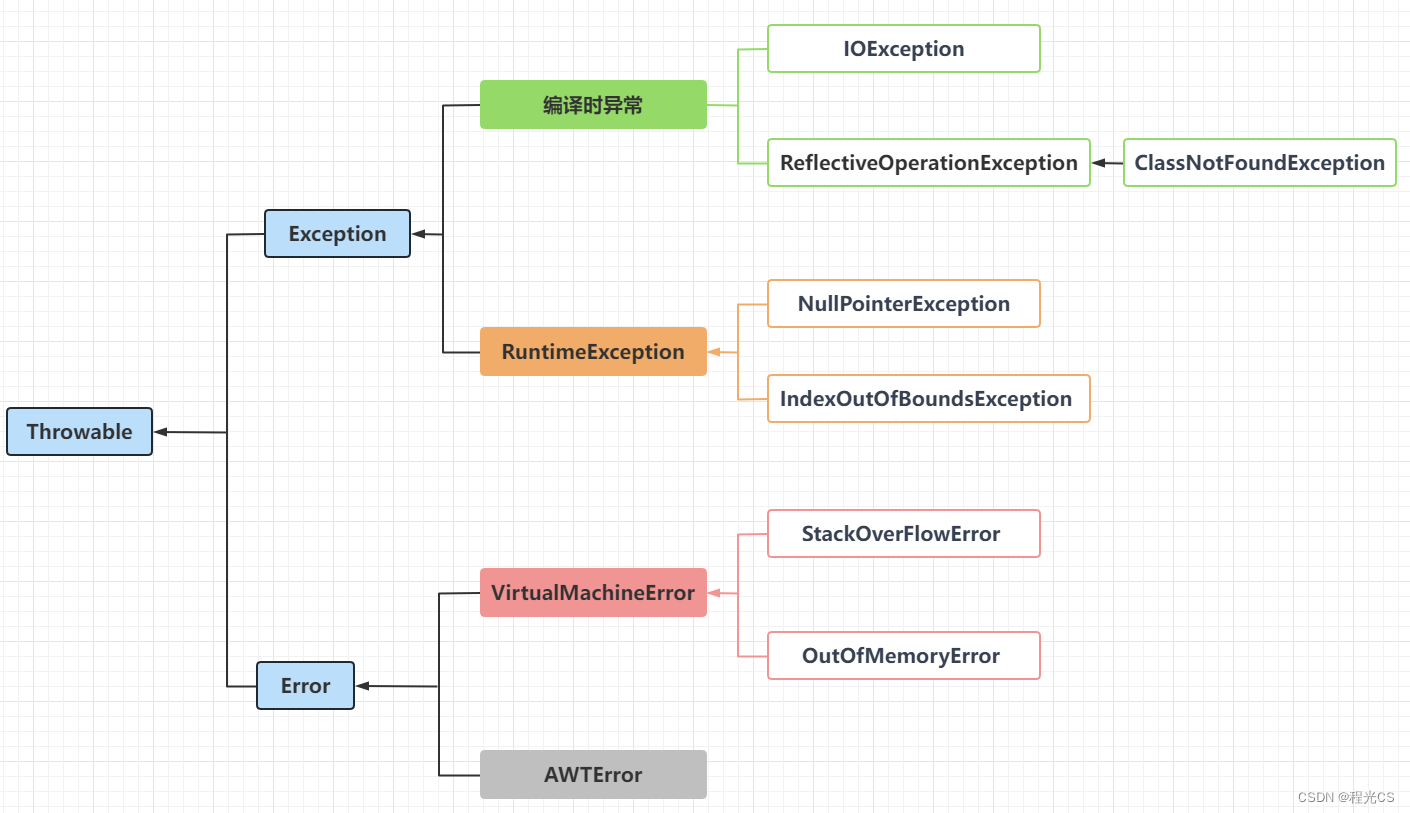
Java异常Throwable的分类
1. Exception:程序本身可以捕获并且可以处理的异常 编译时异常:编译期就会检查的异常,若调用的方法中throw了此类异常,则必须进行显式处理处理(用try…catch捕获或者throws向上抛出),否则无法通…...

【mybatis的#和$使用和区别】
MyBatis是一种基于Java的持久层框架,用于将数据库操作和Java对象之间的映射进行处理。在MyBatis中,#和 $ 符号是用于SQL语句中的占位符。 在SQL语句中,#和 $ 符号都表示占位符,但它们的使用方式略有不同: # 符号 #符…...

感知趋势,洞察发展:2023(第十届)趋势与预测大会成功举办
2023年2月23日,运联年会:2023(第十届)趋势与预测大会在深圳机场凯悦酒店成功闭幕。自2014年开始,“运联年会:趋势与预测”已经连续举办九届。这场大会,既是一次行业性的“年终总结”,…...

Spring-Aop核心技术
前言spring一直以来都是我们Java开发中最核心的一个技术,其中又以ioc和aop为主要技术,本篇文章主要讲一下aop的核心技术,也就是ProxyFactory技术的使用,而基本的jdk动态代理和cglib代理技术并不涉及,如有需要ÿ…...

webpack常用优化原理剖析
webpack常用优化原理剖析 按需加载代码配置原理CDN加速-externals代码配置GZIP压缩代码配置原理Tree Shaking代码配置原理按需加载 把不同路由对应的组件分割成不同的代码块,然后当路由被访问的时候才加载对应组件. 代码配置 //定义了一个异步函数,由于函数不调用不执行,所…...

【现在努力还不晚】--MySQL数据库的数据模型
目录 1、关系型数据库(RDBMS) 特点 2、数据模型 在学习MySQL之前要了解一下数据库的数据模型,我们就知道在MySQL当中,数据是如何存储的,我们了解一下概念! 1、关系型数据库(RDBMS࿰…...
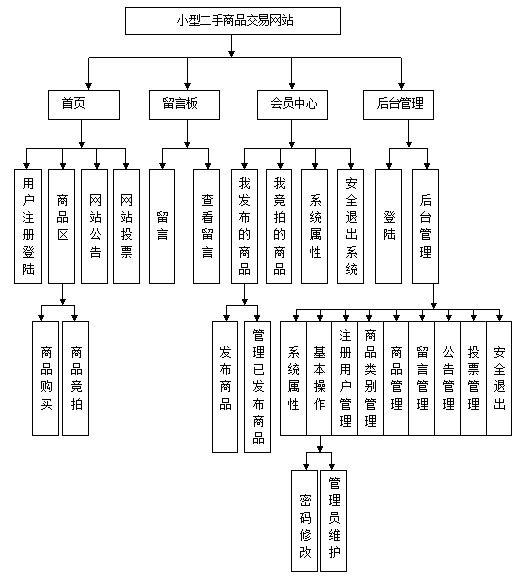
二手商品交易网站
技术:Java、JSP等摘要:随着科学技术和信息通讯的飞速发展,Internet极大地丰富和改变着我们生活的各个行业。随着Internet的普及应用,人们可以跨越时间和空间的限制,足不出户便能通过网络完成信息交流,而完成…...
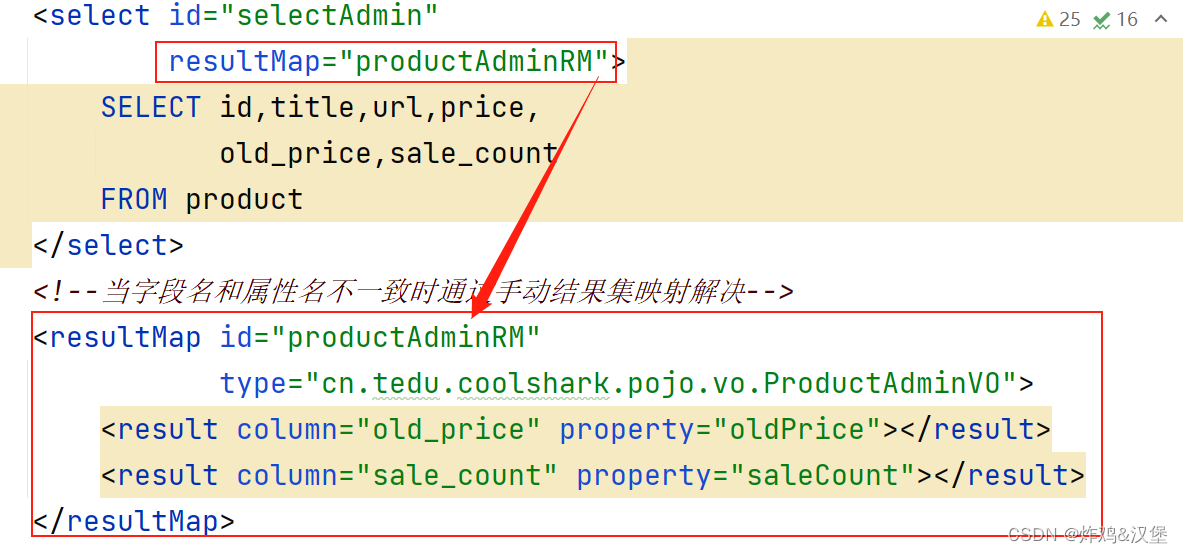
第三阶段04-同步请求和异步请求,get/post,Josn,pojo,Session/Cookie,过滤器Filter
文章目录同步请求和异步请求客户端如何发出异步请求自定义模板代码Get和Post请求异步版本的注册和登录商品管理系统(异步版本)商品列表步骤:前后端分离为什么需要前后端分离?为什么以后不再使用同步请求?JSONPOJO会话对象Session如何记住登录状态后端的MVC会话管理Cookie通过…...

Spark学习:spark相似算子解析
spark算子 一、Map、Flatmap和MapPartition二、repartition和coalesce三、reduceByKey和groupByKey四、collect、take和first一、Map、Flatmap和MapPartition 算子作用map接收一个高阶函数f,对每个算子进行f操作flatmap接收一个高阶函数f,对每个元素进行f操作,形成一个大的集合…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
