二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案
文章目录
- 二分查找与二分答案
- 应用总结
- 例题
- 木材加工
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 数据规模与约定
- 思路
- 代码
- 递归与递推
- 应用总结
- [NOIP2003 普及组] 栈
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- 代码
- acwing3777. 砖块
- 思路
- 代码
- 费解的开关
- 思路
- 代码
- 约数之和
- 思路
- 代码
- 并查集
- 概述
- 食物链
- 思路
- 代码
- 银河英雄传说
- 思路
- 代码
- 单调队列
- 应用概述
- AcWing 135. 最大子序和
- 思路
- 代码
- AcWing 1089. 烽火传递
- 思路
- 代码
应用总结
一般应用于求解最值或者具体某个数的并具有单调性的问题
例题
木材加工
题目背景
要保护环境
题目描述
木材厂有 nnn 根原木,现在想把这些木头切割成 kkk 段长度均为 lll 的小段木头(木头有可能有剩余)。
当然,我们希望得到的小段木头越长越好,请求出 lll 的最大值。
木头长度的单位是 cm\text{cm}cm,原木的长度都是正整数,我们要求切割得到的小段木头的长度也是正整数。
例如有两根原木长度分别为 111111 和 212121,要求切割成等长的 666 段,很明显能切割出来的小段木头长度最长为 555。
输入格式
第一行是两个正整数 n,kn,kn,k,分别表示原木的数量,需要得到的小段的数量。
接下来 nnn 行,每行一个正整数 LiL_iLi,表示一根原木的长度。
输出格式
仅一行,即 lll 的最大值。
如果连 1cm\text{1cm}1cm 长的小段都切不出来,输出 0。
样例 #1
样例输入 #1
3 7
232
124
456
样例输出 #1
114
提示
数据规模与约定
对于 100%100\%100% 的数据,有 1≤n≤1051\le n\le 10^51≤n≤105,1≤k≤1081\le k\le 10^81≤k≤108,1≤Li≤108(i∈[1,n])1\le L_i\le 10^8(i\in[1,n])1≤Li≤108(i∈[1,n])。
思路
对于一些求最值问题,如果检验函数具有一定的单调性,可以使用二分法来求解答案。
就本题具体来说,检验函数用于检验分段长度n是否可以将所有原木切割成k段均为l的小木头。这是我们只需要检验n分割原木,所切割的段数是否大于k即可。当n越大可以分割的段数越少,所以具有一定的单调性。
二分即找到可行区间:为左半段,最值即右端点。
代码
def check(x) : # 用于检验划分长度为x时是否合法cnt = 0for i in sticks :cnt += i // xreturn cnt >= msticks = []
n, m = map(int, input().split())
for i in range(n) :sticks.append(int(input()))
# 左半段二分模板
l, r = 0, sum(sticks)
while l < r :mid = (l + r + 1) >> 1if check(mid) : l = midelse : r = mid - 1
print(l)
递归与递推
应用总结
- 递推
释义:递是传递,是不同问题规模之间的关系;推是求解方向,即由问题边界出发,正向推出问题的解。每次向规模更大的方向推出时,求解方法一致,从而单向遍历了整个状态空间。
递推的关键是找到问题边界,可能问题边界需要自己来计算,比如费解的开关一题 - 递归
释义:递是向下传递的动作,是将大数据规模的问题拆分成小数据规模的问题;而归是对小问题规模的解进行整合,从而获得大规模问题的解
递归的关键是,缩小问题,求解问题,扩展问题
[NOIP2003 普及组] 栈
题目背景
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即 pop(从栈顶弹出一个元素)和 push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
题目描述
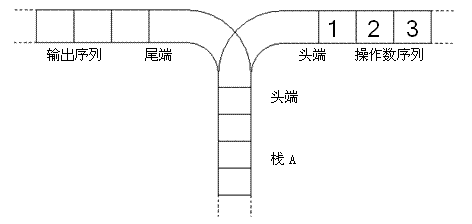
宁宁考虑的是这样一个问题:一个操作数序列,1,2,…,n1,2,\ldots ,n1,2,…,n(图示为 1 到 3 的情况),栈 A 的深度大于 nnn。
现在可以进行两种操作,
- 将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的 push 操作)
- 将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的 pop 操作)
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列,下图所示为由 1 2 3 生成序列 2 3 1 的过程。
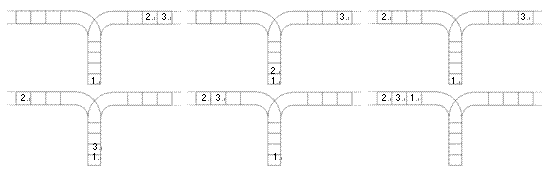
(原始状态如上图所示)
你的程序将对给定的 nnn,计算并输出由操作数序列 1,2,…,n1,2,\ldots,n1,2,…,n 经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 nnn(1≤n≤181 \leq n \leq 181≤n≤18)。
输出格式
输出文件只有一行,即可能输出序列的总数目。
样例 #1
样例输入 #1
3
样例输出 #1
5
提示
【题目来源】
NOIP 2003 普及组第三题
思路
对于原问题大规模的回答较为困难,但我们已知,当操作数序列中元素个数为1时,答案是1。我们试着能否直接推导出结果,此时需要运用的是动态规划的思想。
边界是操作最终的状态
状态表示f[i, j] :
集合:表示栈中包含i个元素,操作序列中包含j个元素时,输出序列的集合。
属性:num
状态计算:f[i, j] = f[i - 1, j] + f[i + 1, j - 1]
也就是操作后状态可能是出栈的情况,或者操作序列压入栈的情况
这类递推公式,有加有减的情况,最好的办法是记忆化搜索。
导向结果的边界不好确定或者是顺序不确定,用递归,否则用递推。
代码
N = 20
f = [[-1] * N for _ in range(N)]
# 记忆化搜索
def dfs(x, y) :if f[x][y] != -1 : return f[x][y]f[x][y] = 0if x - 1 >= 0 :f[x][y] += dfs(x - 1, y)if x + 1 <= n and y - 1 >= 0 :f[x][y] += dfs(x + 1, y - 1)return f[x][y]n = int(input())
# 初始化边界
f[0][0] = 0
for i in range(1, n + 1) :f[i][0] = 1
print(dfs(0, n))
acwing3777. 砖块
n 个砖块排成一排,从左到右编号依次为 1∼n
。
每个砖块要么是黑色的,要么是白色的。
现在你可以进行以下操作若干次(可以是 0
次):
选择两个相邻的砖块,反转它们的颜色。(黑变白,白变黑)
你的目标是通过不超过 3n
次操作,将所有砖块的颜色变得一致。
输入格式
第一行包含整数 T
,表示共有 T
组测试数据。
每组数据第一行包含一个整数 n
。
第二行包含一个长度为 n
的字符串 s
。其中的每个字符都是 W 或 B,如果第 i
个字符是 W,则表示第 i
号砖块是白色的,如果第 i
个字符是 B,则表示第 i
个砖块是黑色的。
输出格式
每组数据,如果无解则输出一行 −1
。
否则,首先输出一行 k
,表示需要的操作次数。
如果 k>0
,则还需再输出一行 k
个整数,p1,p2,…,pk
。其中 pi
表示第 i
次操作,选中的砖块为 pi
和 pi+1
号砖块。
如果方案不唯一,则输出任意合理方案即可。
数据范围
1≤T≤10
,
2≤n≤200
。
输入样例:
4
8
BWWWWWWB
4
BWBB
5
WWWWW
3
BWB
输出样例:
3
6 2 4
-1
0
2
2 1
思路
本题首先明确:
- 每个位置只能操作0或1次
- 操作顺序无影响,默认从左到右
- 最终状态要么全白要么全黑
那么这样只要确定了第一个位置的操作,后序的操作便被确定,这是一个递推的过程。
代码
T = int(input())def check(s, target) :length = len(s)res = []for i in range(length - 1) :if s[i] == target :continueelse :res.append(i)if s[i] == 'W' :s[i] = 'B'else :s[i] = 'W'if s[i + 1] == 'W' :s[i + 1] = 'B'else :s[i + 1] = 'W'if s[-1] != target : return Falseprint(len(res))if len(res) :for i in res :print(i + 1, end = " ")print()return True
for _ in range(T) :n = int(input())s = input()if not check(list(s), 'B') and not check(list(s), 'W') :print(-1)
费解的开关
你玩过“拉灯”游戏吗?
25
盏灯排成一个 5×5
的方形。
每一个灯都有一个开关,游戏者可以改变它的状态。
每一步,游戏者可以改变某一个灯的状态。
游戏者改变一个灯的状态会产生连锁反应:和这个灯上下左右相邻的灯也要相应地改变其状态。
我们用数字 1
表示一盏开着的灯,用数字 0
表示关着的灯。
下面这种状态
10111
01101
10111
10000
11011
在改变了最左上角的灯的状态后将变成:
01111
11101
10111
10000
11011
再改变它正中间的灯后状态将变成:
01111
11001
11001
10100
11011
给定一些游戏的初始状态,编写程序判断游戏者是否可能在 6
步以内使所有的灯都变亮。
输入格式
第一行输入正整数 n
,代表数据中共有 n
个待解决的游戏初始状态。
以下若干行数据分为 n
组,每组数据有 5
行,每行 5
个字符。
每组数据描述了一个游戏的初始状态。
各组数据间用一个空行分隔。
输出格式
一共输出 n
行数据,每行有一个小于等于 6
的整数,它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。
对于某一个游戏初始状态,若 6
步以内无法使所有灯变亮,则输出 −1
。
数据范围
0<n≤500
输入样例:
3
00111
01011
10001
11010
11100
11101
11101
11110
11111
11111
01111
11111
11111
11111
11111
输出样例:
3
2
-1
思路
首先,每个灯作为中心点最多只能操作一次,顺序无所谓。
那么当前面一行操作后,当前行所做的操作是,必须将前面一行全部点亮。所以确定了一行就能确定后面所有行的状态。
我们通过枚举第一行所有可能的状态,来确定最后所有可能的操作。
代码
import copy
DIRC = [[-1, 0], [0, 1], [1, 0], [0, -1]]
def turn(x, y) : # 将以(x, y)为中心的五个灯按一下a[x][y] ^= 1for i in range(4) :x1, y1 = x + DIRC[i][0], y + DIRC[i][1]if 0 <= x1 <= 4 and 0 <= y1 <= 4 :a[x1][y1] ^= 1
def work() :global atmp = copy.deepcopy(a)res = 10000010for i in range(1 << 5) : # 枚举第一行的操作cnt = 0 # 记录操作数for j in range(5) :if i >> j & 1 == 0 :cnt += 1turn(0, j)for j in range(4) : # 递推后面几行for k in range(5) :if a[j][k] == 0 :cnt += 1turn(j + 1, k)flag = True # 判断操作是否成功for j in range(5) :if a[-1][j] == 0 :flag = Falsebreakif flag :res = min(res, cnt)a = copy.deepcopy(tmp)if res <= 6 :print(res)else :print(-1)T = int(input())
a = []
for t in range(T) :a = []for i in range(5) :a.append(list(map(int, list(input()))))if t < T - 1 :input()work()
约数之和
假设现在有两个自然数 A
和 B
,S
是 AB
的所有约数之和。
请你求出 S mod 9901
的值是多少。
输入格式
在一行中输入用空格隔开的两个整数 A
和 B
。
输出格式
输出一个整数,代表 S mod 9901
的值。
数据范围
0≤A,B≤5×107
输入样例:
2 3
输出样例:
15
注意: A
和 B
不会同时为 0。
思路
对于一个数,可以写成质因数形式。即
则由约数个数定理可知的正约数有个 ,
,
那么的个正约数的和为 。
。
本题指数范围比较大,需要我们使用到分治的思想。
对于p10+p11+p12+...+p1a1p_1^0 + p_1^1+p_1^2+...+p_1^{a_1}p10+p11+p12+...+p1a1来说
如果a1a_1a1为奇数,则可表示为p10+p11+p12+...+p1a12+p1a12+1+...+p1a1p_1^0 + p_1^1+p_1^2+...+p_1^{\cfrac{a_1}{2} } +p_1^{\cfrac{a_1}{2} + 1}+...+p_1^{a_1}p10+p11+p12+...+p12a1+p12a1+1+...+p1a1
等价于(1+p1a12+1)∗(p10+p11+p12+...+p1a12)(1+p_1^{\cfrac{a_1}{2} + 1})*(p_1^0 + p_1^1+p_1^2+...+p_1^{\cfrac{a_1}{2} })(1+p12a1+1)∗(p10+p11+p12+...+p12a1)
如果a1a_1a1是偶数,则可表示为(1+p1a12)∗(p10+p11+p12+...+p1a12−1)+p1a1(1 + p_1^{\cfrac{a_1}{2}})*(p_1^0 + p_1^1+p_1^2+...+p_1^{\cfrac{a_1}{2} -1} ) + p_1^{a_1}(1+p12a1)∗(p10+p11+p12+...+p12a1−1)+p1a1,按照这种思路逐步递归。
代码
MOD = 9901
# 快速幂
def q_mi(a, b) :if a == 0 :return 0res = 1while b :if b & 1 :res = (res * a) % MODb >>= 1a = (a * a) % MODreturn resdef figure(a, b) :if b == 0 :return 1if b % 2 :return (1 + q_mi(a, b // 2 + 1)) * figure(a, b // 2) % MODelse :return (1 + q_mi(a, b // 2)) * figure(a, b // 2 - 1) + q_mi(a, b) % MODn, m = map(int, input().split())
ans = 1
# 求质因子
i = 2
while i <= n // i :s = 0while n % i == 0 :s += 1n //= iif s :ans = (ans * figure(i, s * m)) % MODi += 1
if n > 1 :ans = (ans * figure(n, m)) % MODif n == 0 : print(0)
else :print(ans)
并查集
概述
一般的并查集主要记录节点之间的链接关系,而没有其他的具体的信息,仅仅代表某个节点与其父节点之间存在联系,它多用来判断图的连通性。
带权并查集记录的是节点与代表元节点之间的一定权值关系,节点与节点之前的权值关系通过相减可得。(前缀和思想)
食物链
动物王国中有三类动物 A,B,C
,这三类动物的食物链构成了有趣的环形。
A
吃 B
,B
吃 C
,C
吃 A
。
现有 N
个动物,以 1∼N
编号。
每个动物都是 A,B,C
中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N
个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X
和 Y
是同类。
第二种说法是 2 X Y,表示 X
吃 Y
。
此人对 N
个动物,用上述两种说法,一句接一句地说出 K
句话,这 K
句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话;
当前的话中 X
或 Y
比 N
大,就是假话;
当前的话表示 X
吃 X
,就是假话。
你的任务是根据给定的 N
和 K
句话,输出假话的总数。
输入格式
第一行是两个整数 N
和 K
,以一个空格分隔。
以下 K
行每行是三个正整数 D,X,Y
,两数之间用一个空格隔开,其中 D
表示说法的种类。
若 D=1
,则表示 X
和 Y
是同类。
若 D=2
,则表示 X
吃 Y
。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000
,
0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
思路
本题的带权并查集主要记录的是,到根节点的路径上有多少个节点。
代码
N = 50010
p = [0] * N
d = [0] * Ndef init() :for i in range(1, n + 1) :p[i] = idef find(x) :if p[x] != x :t = find(p[x])d[x] += d[p[x]] # 更新到根节点路径上的节点数p[x] = treturn p[x]n, m = map(int, input().split())
init()cnt = 0
for _ in range(m) :op, x, y = map(int, input().split())if x > n or y > n : # 第一类错误cnt += 1continuefx, fy = find(x), find(y)if op == 1:if fx == fy and (d[x] - d[y]) % 3 : # 0表示同类,判断过非同类cnt += 1elif fx != fy :p[fx] = fyd[fx] = d[y] - d[x] # 同类d[x] + d[fx]与d[y]同模else :if fx == fy and (d[x] - d[y] - 1) % 3 : cnt += 1 # 判断过非x吃yelif fx != fy :p[fx] = fyd[fx] = d[y] - d[x] + 1
print(cnt)
银河英雄传说
有一个划分为 N
列的星际战场,各列依次编号为 1,2,…,N
。
有 N
艘战舰,也依次编号为 1,2,…,N
,其中第 i
号战舰处于第 i
列。
有 T
条指令,每条指令格式为以下两种之一:
M i j,表示让第 i
号战舰所在列的全部战舰保持原有顺序,接在第 j
号战舰所在列的尾部。
C i j,表示询问第 i
号战舰与第 j
号战舰当前是否处于同一列中,如果在同一列中,它们之间间隔了多少艘战舰。
现在需要你编写一个程序,处理一系列的指令。
输入格式
第一行包含整数 T
,表示共有 T
条指令。
接下来 T
行,每行一个指令,指令有两种形式:M i j 或 C i j。
其中 M
和 C
为大写字母表示指令类型,i
和 j
为整数,表示指令涉及的战舰编号。
输出格式
你的程序应当依次对输入的每一条指令进行分析和处理:
如果是 M i j 形式,则表示舰队排列发生了变化,你的程序要注意到这一点,但是不要输出任何信息;
如果是 C i j 形式,你的程序要输出一行,仅包含一个整数,表示在同一列上,第 i
号战舰与第 j
号战舰之间布置的战舰数目,如果第 i
号战舰与第 j
号战舰当前不在同一列上,则输出 −1
。
数据范围
N≤30000,T≤500000
输入样例:
4
M 2 3
C 1 2
M 2 4
C 4 2
输出样例:
-1
1
思路
这道题的带权并查集的权值表示的是,该元素合并时代表元集合内所有的元素个数,也就是表示该元素在队列中所处位次。
代码
N = 30010p = [0] * N
d = [0] * N
sz = [1] * Ndef init() :for i in range(1, N) :p[i] = i
def find(x) :if x != p[x] :t = find(p[x])d[x] += d[p[x]]p[x] = treturn p[x]T = int(input())
init()
for _ in range(T) : cmd = input().split()x, y = int(cmd[1]), int(cmd[2])fx, fy = find(x), find(y)if cmd[0] == 'M' :if fx != fy :p[fx] = fyd[fx] = sz[fy] # x所处位次为y列最后sz[fy] += sz[fx] # 更新y列的元素个数else :if fx != fy :print(-1)else :print(max(abs(d[x] - d[y]) - 1, 0))
单调队列
应用概述
维护一段窗口固定的按原数组顺序排序的单调序列,用于查找一段固定长度的最大(单调递增队列)最小(单调递减队列)值,常用于优化动态规划。
AcWing 135. 最大子序和
输入一个长度为 n
的整数序列,从中找出一段长度不超过 m
的连续子序列,使得子序列中所有数的和最大。
注意: 子序列的长度至少是 1
。
输入格式
第一行输入两个整数 n,m
。
第二行输入 n
个数,代表长度为 n
的整数序列。
同一行数之间用空格隔开。
输出格式
输出一个整数,代表该序列的最大子序和。
数据范围
1≤n,m≤300000
输入样例:
6 4
1 -3 5 1 -2 3
输出样例:
7
思路
前缀和+单调队列
求一段区间内的数的和,当然就想到前缀和。但要求这个不超过m的段,此时就想到当前位置i之前的前i个位置的一个情况。要求最大值,这就要求我们维护包含i的一个大小为m的窗口,但由于前缀和,总是减去前面一个数,所以窗口大小应该为m+1。
代码
N = 300010
a = [0] * N
q = [0] * Nn, m = map(int, input().split())
a[1 : n + 1] = list(map(int, input().split()))# 前缀和
for i in range(1, n + 1) :a[i] += a[i - 1]
# 单调队列实现结合最大字段和
ans = -1000010
hh, tt = 0, 0 # 刚开始包含前缀0
for i in range(1, n + 1) :while hh <= tt and i - q[hh] > m : # 维护一个m + 1的窗口hh += 1ans = max(ans, a[i] - a[q[hh]])while hh <= tt and a[q[tt]] >= a[i] :tt -= 1tt += 1q[tt] = i
print(ans)
AcWing 1089. 烽火传递
烽火台是重要的军事防御设施,一般建在交通要道或险要处。
一旦有军情发生,则白天用浓烟,晚上有火光传递军情。
在某两个城市之间有 n
座烽火台,每个烽火台发出信号都有一定的代价。
为了使情报准确传递,在连续 m
个烽火台中至少要有一个发出信号。
现在输入 n,m
和每个烽火台的代价,请计算在两城市之间准确传递情报所需花费的总代价最少为多少。
输入格式
第一行是两个整数 n,m
,具体含义见题目描述;
第二行 n
个整数表示每个烽火台的代价 ai
。
输出格式
输出仅一个整数,表示最小代价。
数据范围
1≤m≤n≤2×105
,
0≤ai≤1000
输入样例:
5 3
1 2 5 6 2
输出样例:
4
思路
一道dp题,不过需要用单调队列优化。
状态表示:f[i]
集合:表示前i座烽火台按要求点燃且第i座点燃的代价集合
属性:min
状态计算:
f[i]=min(f[j])+w[i],j=i−m...i−1f[i] = min(f[j]) + w[i], j =i - m ~... ~i - 1f[i]=min(f[j])+w[i],j=i−m ... i−1
代码
N = 200010
f = [0] * N
a = [0] * N
q = [0] * Nn, m = map(int, input().split())a[1 : n + 1] = list(map(int, input().split()))
hh, tt = 0, 0
for i in range(1, n + 1) :while hh <= tt and i - q[hh] > m :hh += 1f[i] = f[q[hh]] + a[i]while hh <= tt and f[q[tt]] >= f[i] :tt -= 1tt += 1q[tt] = i
ans = 1000010
for i in range(n - m + 1, n + 1) :ans = min(ans, f[i])
print(ans)
相关文章:

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
LabVIEW网络服务安全2
LabVIEW网络服务安全2在客户端应用程序中创建签名对请求进行签名要求您具有能够从客户端的编程语言调用的MD5摘要算法以及SHA256加密摘要算法的实现。这两种算法通常都可用于大多数平台。还需要:1. 要使用的HTTP方法的字符串(“GET”、“POST”、“PUT”…...
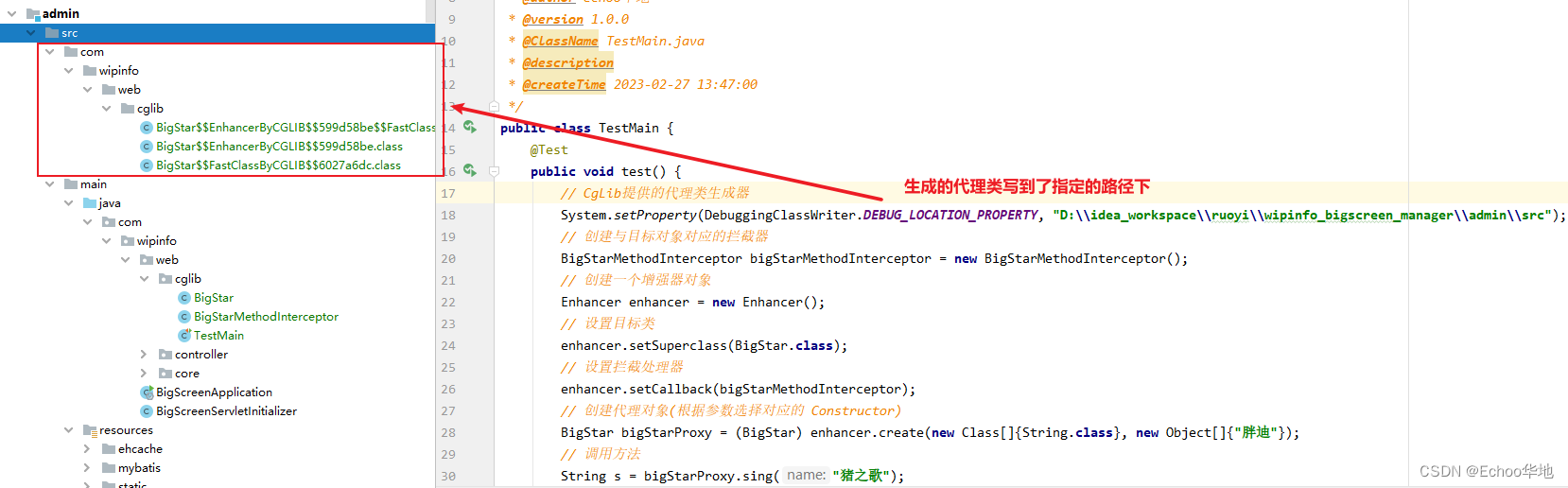
java动态代理
目录儿一、代理模式的作用二、实现代理的方式三、动态代理的实现3.1 jdk动态代理3.2 cglib动态代理一、代理模式的作用 功能增强: 基于某个功能,再增加一些功能。 (比如目标类只负责核心功能,其他附属功能通过代理类完成。代理类的方法名与目…...
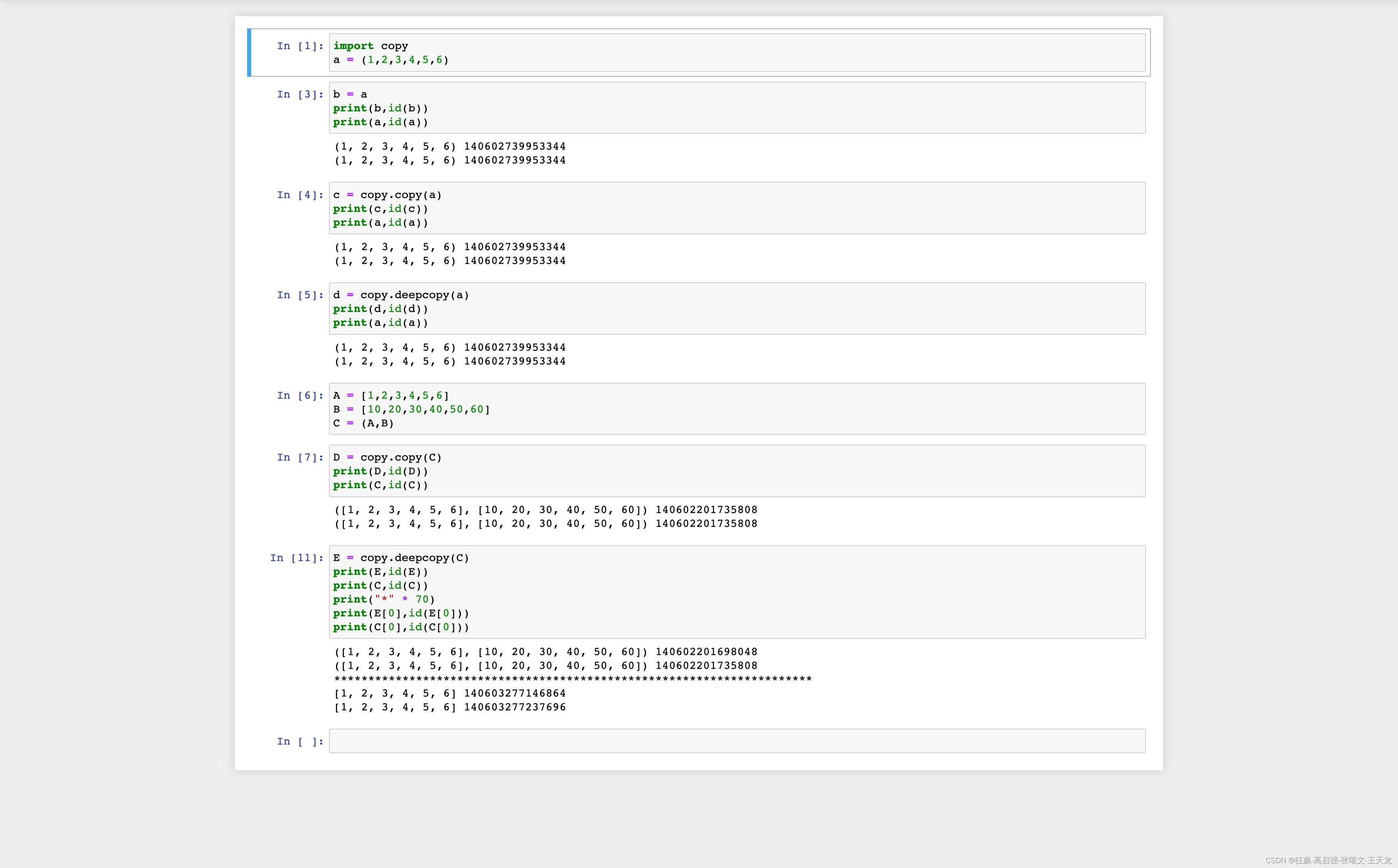
Python 简单可变、复杂可变、简单不可变、复杂不可变类型的copy、deepcopy的行为
copy模块:copy:浅拷贝deepcopy:深拷贝简单可变类型、复杂可变的copy()、deepcopy():简单不可变、复杂不可变类型的copy()、deepcopy():结论:对于简单类型的可变类型copy是深拷贝,改变了该拷贝变…...
QML Item
在QML中所有的可视项目都继承自Item,虽然Item本身没有可视化的外观,但它定义了可视化项目的所有属性。 Item可以作为容器使用: Item{Rectangle{id:retc}Rectangle{id:retc1}Rectangle{id:retc2}Rectangle{id:retc3}} item拥有children属性…...
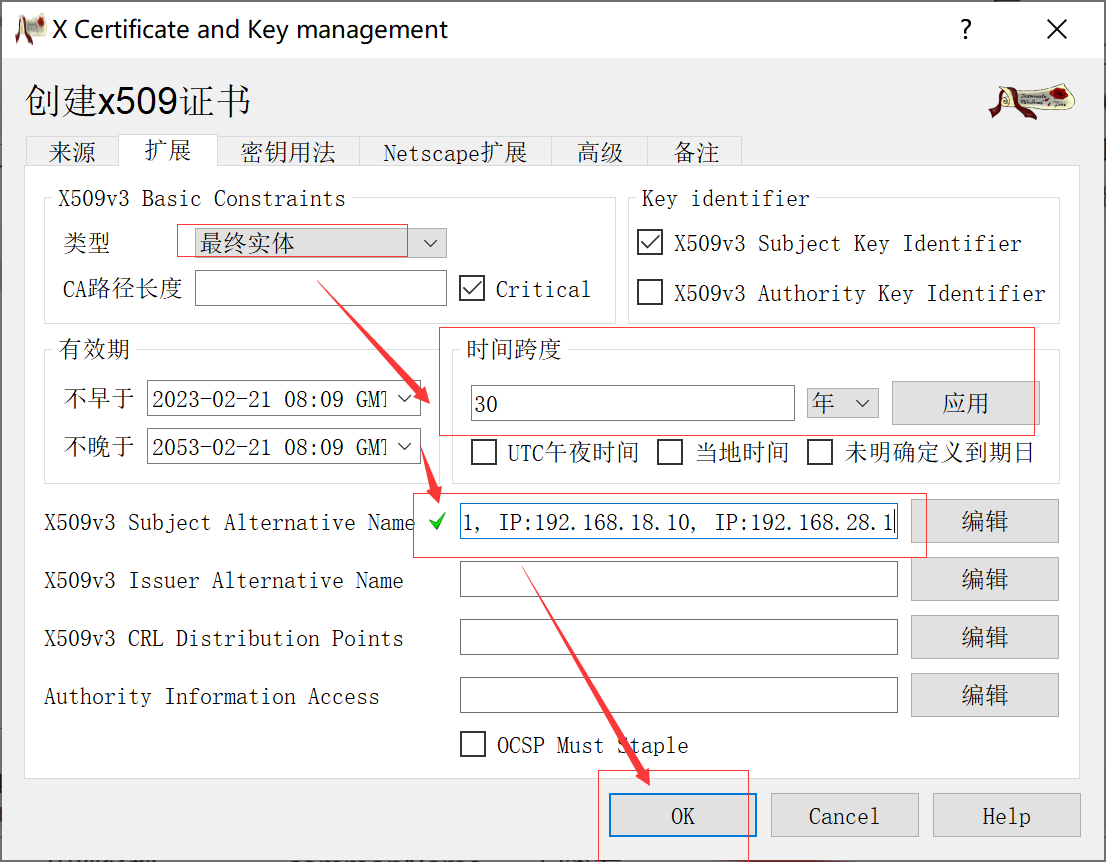
使用xca工具生成自签证书
本文使用 xca 生成自签证书。 概述 之前使用 openssl 生成证书,在 golang 中测试,发现客户端连接失败,经查发现是Subject Alternative Name不支持导致的。因虚拟机 openssl 版本较低,有个功能无法实现,且升级麻烦&…...

Unity IOS 通过命令行导出IPA
新建一个文件然后输入如下内容 #!/usr/bin/env sh /Applications/Unity/Hub/Editor/2020.1.5f1c1/Unity.app/Contents/MacOS/Unity -quit -batchmode -projectPath /Users/zyt/Test -executeMethod Test.BuildEditor.BuildApp cd /Users/zyt/Test/Xcode/unity-xcode xcodebuil…...
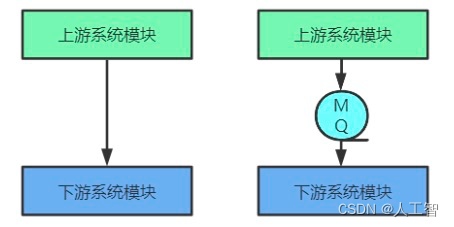
「架构」全链路异步模式
总结自尼恩的全链路异步:网关纯异步化网关层的特点:不需要访问业务数据库只做协议转换和流量转发特点是 IO 密集型,特别适合纯异步的架构,可以极大的节省资源。如何进行网关异步化?使用高性能的通信框架Nettyÿ…...
CleanMyMac4.20最新版新增功能及电脑清理垃圾使用教程
CleanMyMac4.20作为知名的Mac清理工具,仅需一键即可快速而安全地清理系统垃圾,释放磁盘空间,因此一直深受Mac用户的喜爱。在不断更新的版本中,CleanMyMac已经不仅仅满足于只做简单的Mac清理工具,而是为Mac用户提供更多…...

Vue2的tsx开发入门完全指南
本篇文章尽量不遗漏重要环节,本着真正分享的心态,不做标题党 下面进入正题: 由于现在vue的官方脚手架已经非常完善我们就不单独配置webpack了,节省大量的时间成本。 首先使用vue/cli创建一个vue模版项目(记得是vue/…...

GLSL shader学习系列1-Hello World
这是GLSL shader系列第一篇文章,本文学习目标: 安装编辑工具编写hello world程序 安装插件 我使用VSCode编写shader代码,在VSCode上有两个好用的插件需要先装一下: Shader languages support for VS Code glsl-canvas…...

Codeforces Round #851 (Div. 2)(A~D)
A. One and Two给出一个数组,该数组仅由1和2组成,问是否有最小的k使得k位置的前缀积和后缀积相等。思路:计算2个数的前缀和即可,遍历判断。AC Code:#include <bits/stdc.h>typedef long long ll; const int N 1…...

内存保护_1:Tricore芯片MPU模块介绍
上一篇 | 返回主目录 | 下一篇 内存保护_1:Tricore芯片MPU模块介绍1 何为MPU2 MPU相关的硬件子系统2.1 基于地址范围保护逻辑说明2.1.1 地址范围寄存器2.1.2 读、写、执行权限寄存器2.1.3 保护集设置位2.1.4 内存保护功能使能位2.1.5 核的内存保护范围获取说明2.1.6…...

Vue3 -- PDF展示、添加签名(带笔锋)、导出
文章目录笔锋签名方案一实现要点实现过程组件引用页面元素添加引用实现代码效果展示缺点方案二修改页面元素替换引用修改代码效果展示完整代码地址实现功能的时候采用了两个方案,主要是第一个方案最后的实现效果并不太理想,但实现起来比较简单࿰…...
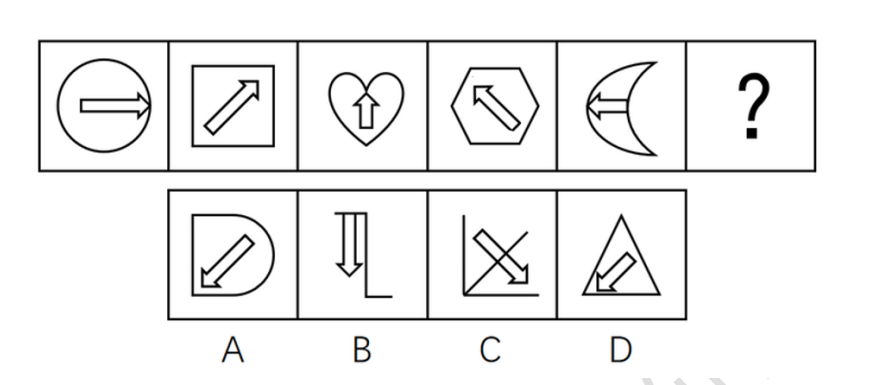
行测-判断推理-图形推理-样式规律-属性规律-曲直性
左边的图全是由曲线构成的选C1 3 5全是由曲线构成的2 4 6全是由直线构成的第三行的图形有曲有直选A1 3 5有曲有直2 4 6全是直线选D图形有曲有直,排除B D外曲内直->内曲外直->外曲内直->内曲外直->外曲内直->内曲外直所以问号出的图形应该是内曲外直选…...

idea集成Alibaba Cloud Toolkit插件
idea集成Alibaba Cloud Toolkit插件 使用该插件主要是简化打包、上传、启动服务的相关操作。 很早之前的方式是使用开发工具(eclipse,idea),使用maven命令完成项目打包(这里指jar),然后通过shell工…...
Win11 文件夹打开慢或卡顿解决方案
问题 目前是 2023/2/27, 我的 Win11 系统点开一个文件夹要等待 2-3 秒才能加载出来, 使用体验极差。网上查阅大量资料, 有些人在系统更新后这个情况就消失了, 但是我这一直存在, 系统也是当前的最新版, 没有修复。 目前得出的结论是, 因为 Win11 的工具栏占用了过多的资源, 需…...
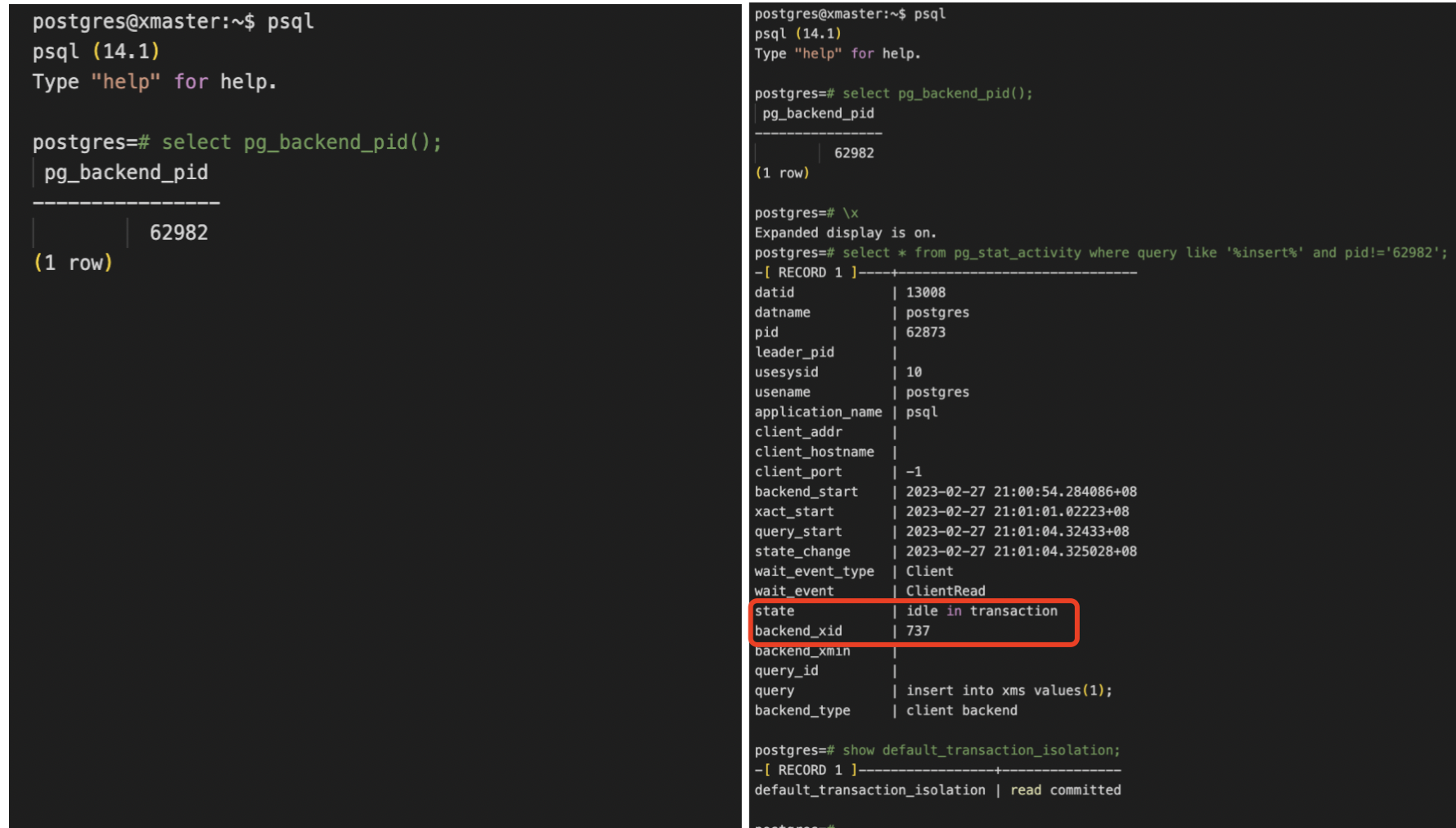
【PostgreSQL的idle in transaction连接状态】
在平时查询pg_stat_activity这个视图的时候,每一行包含了一个进程的相关信息,包含当前正在执行的SQL,或者会话的状态等等,state字段表示当前进程的状态。在PostgreSQL数据库里,其实代码里总共定义了7种BackendState&am…...
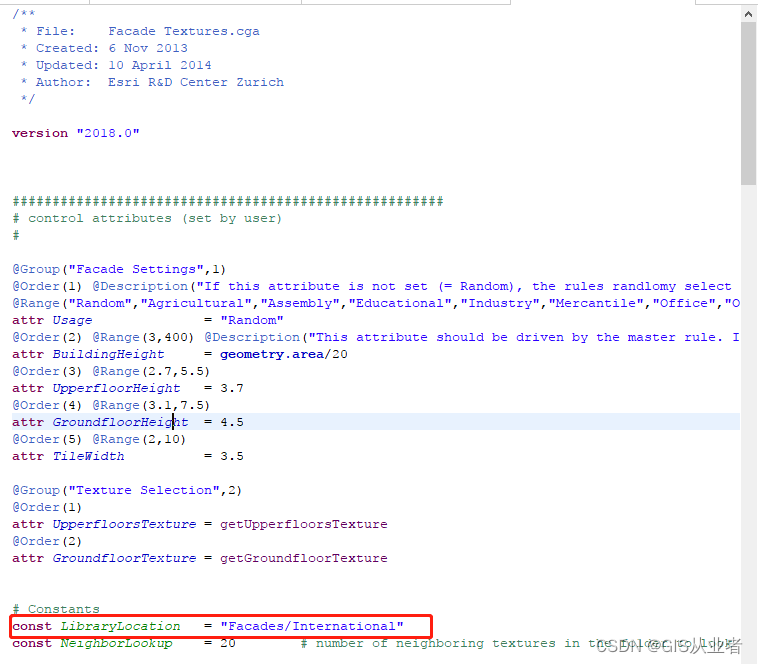
cityengine自定义纹理库资源
背景 cityengine虽然可以将shp生成带纹理的三维模型,但是纹理不一定满足我们的要求,这时候我们就想用我们自己制作的纹理 粗略了解规则文件 了解Building_From_Footprint.cga这个规则文件,具体文件位置默认在 “C:\Users[电脑用户名:如Administrator]\Documents\CityEng…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
