Kafka从安装使用到集成Springboot详细教程
“不积跬步,无以至千里。”
1. 引言
在当今高度互联的技术领域,消息队列成为分布式系统中不可或缺的一部分。Apache Kafka作为一个高性能、持久化、分布式的消息队列系统,备受开发者推崇。这篇文章将从安装到集成Spring的全方位介绍Kafka的使用。
2. Kafka的安装及基本操作
2.1 安装步骤
Kafka的安装可以通过官方网站下载二进制包进行,或者通过包管理工具直接安装。详细步骤请参考官方文档。
2.2 基本概念
在开始Kafka的基本操作之前,了解一些重要的概念是很有帮助的。包括Producer(生产者)、Consumer(消费者)、Topic(主题)等。
2.3 基本操作
- 创建Topic:
bin/kafka-topics.sh --create --bootstrap-server localhost:9092 --replication-factor 1 --partitions 1 --topic myTopic
- 发送消息:
bin/kafka-console-producer.sh --bootstrap-server localhost:9092 --topic myTopic
- 消费消息:
bin/kafka-console-consumer.sh --bootstrap-server localhost:9092 --topic myTopic --from-beginning
3. 命令行操作详解
Kafka提供了丰富的命令行工具,用于管理、监控和操作集群。以下是一些常用命令:
- 查看Topic列表:
bin/kafka-topics.sh --list --bootstrap-server localhost:9092
- 查看Topic详情:
bin/kafka-topics.sh --describe --bootstrap-server localhost:9092 --topic myTopic
- 查看Consumer组:
bin/kafka-consumer-groups.sh --list --bootstrap-server localhost:9092
4. 配置Kafka
Kafka的配置文件server.properties包含了许多参数,可以根据需要进行调整。常见的配置包括Broker ID、端口、日志目录等。详细配置请参考官方文档。
5. 集成Spring
5.1 集成Spring
Kafka提供了Spring Kafka项目,用于简化Kafka在Spring应用中的集成。通过在pom.xml中引入相关依赖,可以轻松实现Producer和Consumer的开发。
<dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId><version>2.7.0</version>
</dependency>
5.2 使用Spring Kafka
5.2.1 生产者
@Service
public class KafkaProducerService {@Autowiredprivate KafkaTemplate<String, String> kafkaTemplate;public void sendMessage(String topic, String message) {kafkaTemplate.send(topic, message);}
}
5.2.2 消费者
@Service
public class KafkaConsumerService {@KafkaListener(topics = "myTopic", groupId = "myGroup")public void listen(String message) {// 处理接收到的消息System.out.println("Received Message: " + message);}
}
6. 集成Spring Boot
6.1 集成Spring Boot
Spring Boot使得Kafka的集成更加简便。只需在application.properties中配置Kafka相关信息,即可启动一个具备Kafka功能的Spring Boot应用。
spring.kafka.bootstrap-servers=localhost:9092
spring.kafka.consumer.group-id=myGroup
6.2 使用Spring Boot
Spring Boot提供了@KafkaListener注解,简化了Consumer的编写,而Producer则可直接使用KafkaTemplate。
@Service
public class KafkaService {@Autowiredprivate KafkaTemplate<String, String> kafkaTemplate;@KafkaListener(topics = "myTopic", groupId = "myGroup")public void listen(String message) {// 处理接收到的消息System.out.println("Received Message: " + message);}public void sendMessage(String topic, String message) {kafkaTemplate.send(topic, message);}
}
7. 总结
通过详细的介绍,想必你已经学会了从Kafka的安装到基本操作,再到命令行操作和配置,最后到如何在Spring和Spring Boot中集成Kafka。Kafka作为一个强大的分布式消息队列系统,为开发者提供了高效可靠的消息传递解决方案。希望这篇博客对你在实际项目中使用Kafka提供了帮助。
相关文章:

Kafka从安装使用到集成Springboot详细教程
“不积跬步,无以至千里。” 1. 引言 在当今高度互联的技术领域,消息队列成为分布式系统中不可或缺的一部分。Apache Kafka作为一个高性能、持久化、分布式的消息队列系统,备受开发者推崇。这篇文章将从安装到集成Spring的全方位介绍Kafka的使…...

【giszz笔记】产品设计标准流程【4】
(续上回) 我们继续把扩展考虑UX环节的产品打造标准流程,来进行梳理。 一千个人心中有一千个哈姆雷特,本文将日常大家耳熟能详,但是又未必人人心中成体系的产品打造标准流程,进行总结。 考虑了两种项目&a…...
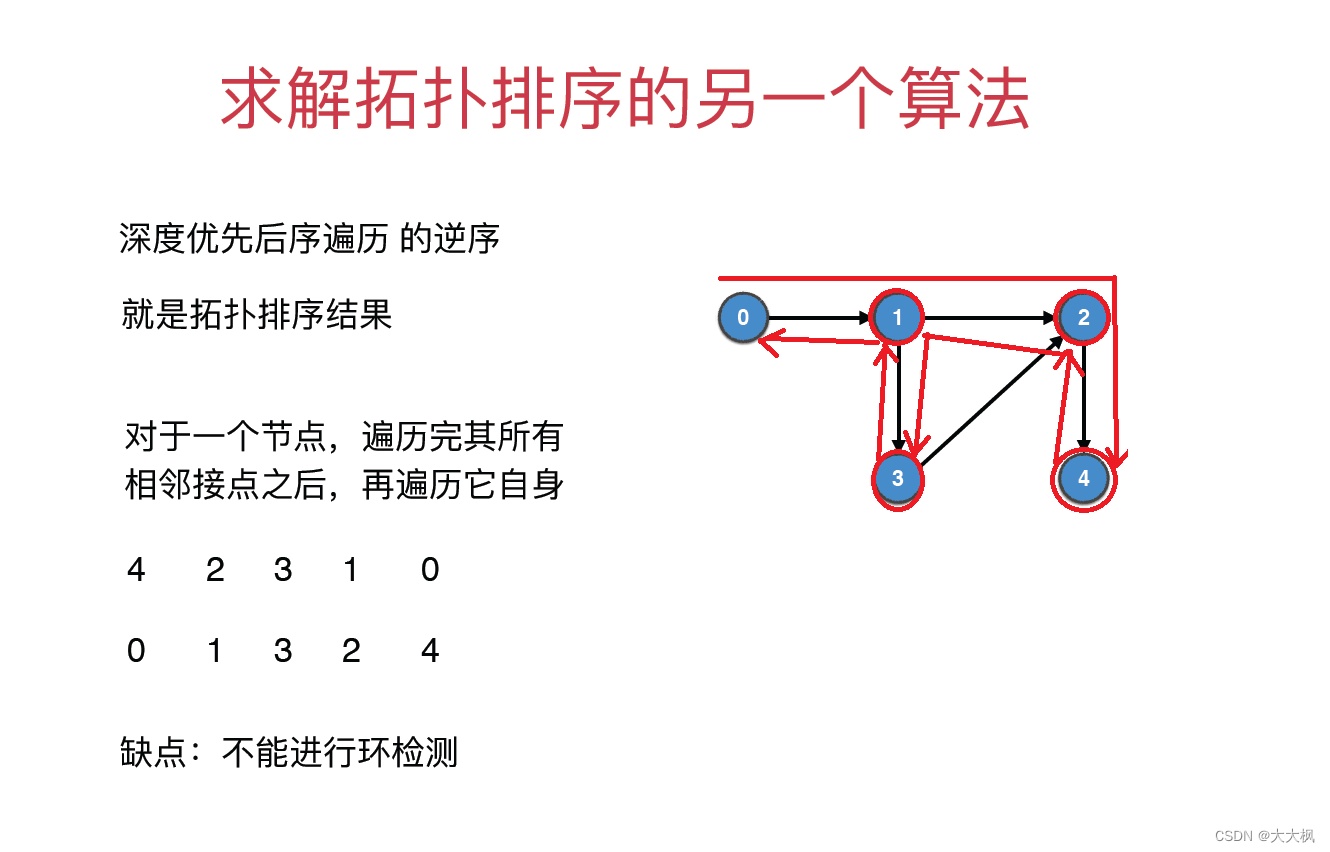
图论16-拓扑排序
文章目录 1 拓扑排序2 拓扑排序的普通实现2.1 算法实现 - 度数为0入队列2.2 拓扑排序中的环检测 3 深度优先遍历的后续遍历3.1 使用环检测类先判断是否有环3.2 调用无向图的深度优先后续遍历方法,进行DFS 1 拓扑排序 对一个有向无环图G进行拓扑排序,是将…...
SecureCRT 9.4.2最新终端SSH工具
SecureCRT是一款终端SSH工具,它提供了类似于Telnet和SSH等协议的远程访问功能。SecureCRT软件特色包括: 支持SSH(SSH1和SSH2)的终端仿真程序,能在Windows下登录UNIX或Linux服务器主机。SecureCRT支持SSH,同…...
基于python+django的美食餐厅点餐订餐网站
运行环境 开发语言:Python python框架:django 软件版本:python3.7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:PyCharm/vscode 前端框架:vue.js 项目介绍 本论文主要论述了如何使用python语言开发…...
Moka人事:实现无代码开发的API连接,打通电商平台与用户运营系统
无代码开发的API连接:Moka人事的核心优势 Moka人事,是北京希瑞亚斯科技有限公司于2015年推出的一款数据驱动的智能化HR SaaS产品。这款产品的主要优势在于其无需进行API开发即可实现系统的连接和集成,这不仅大大提升了企业的工作效率&#x…...

【Spring】超详细讲解AOP(面向切面编程)
文章目录 1. 前言2. 什么是AOP3. AOP快速入门4. AOP的核心概念5. 切点表达式6. 切点函数7. 通知8. 总结 1. 前言 本文围绕AOP进行讲解,AOP可以做什么,涉及到了哪些注解,以及各个注解运行的时机,以及Around相较于其它注解有什么不同,并且如果要执行目标方法需要怎么做 2. 什么…...
界面组件DevExpress Reporting v23.1亮点 - 全新升级报表查看器
DevExpress Reporting是.NET Framework下功能完善的报表平台,它附带了易于使用的Visual Studio报表设计器和丰富的报表控件集,包括数据透视表、图表,因此您可以构建无与伦比、信息清晰的报表 界面组件DevExpress Reporting v23.1已经发布一段…...

电容容量换算电池容量,以及RTC持续时间计算
依据 公式1:QI*t 公式2:QC*U 其中: Q: 电荷量 (库仑) I: 电流 (安培) t: 时间 (秒) C: 电容量 (法拉…...

【BIM入门实战】高程点无法放置的解决方法
文章目录 一、问题提出二、解决办法1. 检查模型图形样式2. 高程点可以放置的图元一、问题提出 在平面图中添加高程点时有时会遇到无法在楼板等平面构件上放置高程点,应如何设置才能使高程点正常放置? 如下图所示,楼板上无法放置高程点: 二、解决办法 1. 检查模型图形样式…...

CRM系统对科技企业有哪些帮助
随着国家政策的倾斜和5G等相关基础技术的发展,中国人工智能产业在各方的共同推动下进入爆发式增长阶段,市场发展潜力巨大。CRM客户管理系统作为当下最热门的企业应用,同样市场前景广阔。那么,CRM系统对科技企业有哪些帮助…...
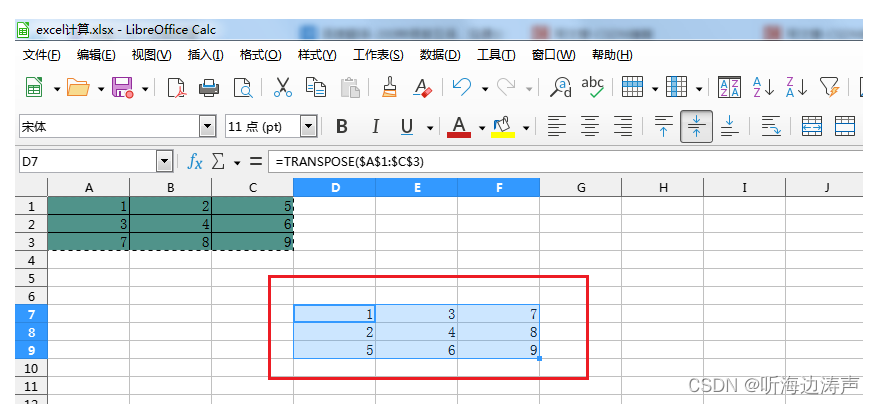
用excel计算一个矩阵的转置矩阵
假设我们的原矩阵是一个3*3的矩阵: 125346789 现在求它的转置矩阵: 鼠标点到一个空白的地方,用来存放结果: 插入-》函数: 选择TRANSPOSE,这个就是求转置矩阵的函数: 点击“继续”:…...

WPF 中的 ControlTemplate 和 DataTemplate 有什么区别
在WPF中,ControlTemplate和DataTemplate都是模板,它们都可以用来定义一段可重复使用的XAML标记。然而,它们的用途和应用场景有很大的不同。 ControlTemplate: ControlTemplate是用来定义控件的外观和视觉行为的。每个WPF控件都有…...

3D重建相关
目录 <font colorblue>整个3D重建的过程是怎样的<font colorblue>体素、网格、点云之间的关系是什么<font colorblue>点云中的颜色怎么处理成最终3D模型上的颜色<font colorblue>点云还原的3D模型的颜色怎么处理,点云有颜色数据?…...
)
字符串数组排序(Java/JavaScript代码版)
Java public static void main(String[] args) throws Exception {String[] arr new String[] {"abc","xyz","efg"};// 默认按自然升序排Arrays.sort(arr);System.out.println(Arrays.toString(arr)); }降序排 降序排,可传入第二个…...

调用电商集成平台 聚水潭 api接口示例
先上工具类 package com.zuodou.utlis;import org.springframework.beans.factory.annotation.Value; import org.springframework.stereotype.Component;import javax.xml.crypto.Data; import java.io.*; import java.net.HttpURLConnection; import java.net.URL; import j…...

深入Rust:探索所有权和借用机制
大家好!我是lincyang。 今天,我们将一起深入探索Rust语言中的一个核心概念:所有权和借用机制。 这些特性是Rust区别于其他语言的重要特点,它们在内存管理和并发编程中扮演着关键角色。 一、Rust所有权机制 1. 什么是所有权&#x…...
)
Python之冒泡排序(AI自动写文章项目测试)
全自动AI生成文章测试,如有不合理地方,请见谅。 一、冒泡排序简介 1.1 冒泡排序概述 冒泡排序(Bubble Sort)是一种简单的排序算法,通过不断交换相邻元素的位置,将最大(或最小)的元…...

spring cloud微服务中多线程下,子线程通过feign调用其它服务,请求头token等丢失
在线程池中,子线程调用其他服务,请求头丢失,token为空的情况 看了很多篇文章的处理方法和在自己亲测的情况下做出说明: 第一种: 这种方式只支持在主线程情况下,能够处理,在多线程情况下&#…...

Nacos 高级玩法:深入探讨分布式配置和服务发现
🎏:你只管努力,剩下的交给时间 🏠 :小破站 Nacos 高级玩法:深入探讨分布式配置和服务发现 前言第一:nacos高级配置管理1. 动态配置的基本使用:2. 监听策略的原理和实现:3…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
