【人脸识别】DDL:数据分布知识蒸馏思想,提升困难样本(遮挡、低分辨率等)识别效果
论文题目:《Improving Face Recognition from Hard Samples via Distribution Distillation Loss》
论文地址:https://arxiv.org/pdf/2002.03662v3.pdf
代码地址:https://github.com/HuangYG123/DDL
1.前言及相关工作
Large facial variations are the main challenge in face recognition。
目前人脸识别面临的主要挑战是大的面部变化(遮挡、姿态如侧脸、低分辨率、种族、光照等)。
解决方式及缺点:
- variation-specific:在设计特殊网络损失之前充分利用了与任务相关的方法,即针对不同的问题设计特定的算法。如姿态(pose-invatiant、face frontalization),分辨率(super- resolution),遮挡模型等。
缺点:在不同的任务和场景中通常是不通用的。 - generic methods:侧重于提高特征可辨别性以最小化类内距离同时最大化类间距离。如margin-based loss(cosface、arcface),metric learning(triplet loss)等。
缺点:在简单样本上表现良好但在困难样本上表现不佳。
DDL:
为了提高困难样本的性能,我们提出了一种新颖的 Distribution Distillation Loss (分布式蒸馏)来缩小简单样本和困难样本之间的性能差距,该方法简单、有效且通用,适用于各种类型的面部变化。 具体来说,我们首先采用最先进的分类器(如 Arcface)来构建两个相似性分布:来自简单样本的教师分布(例如图1中d3的简单样本)和来自困难样本的学生分布(例如图1中d1的困难样本)。 然后,我们提出了一种新的分布驱动损失来约束学生分布以近似教师分布,从而实现学生分布中正负对之间的重叠更小。
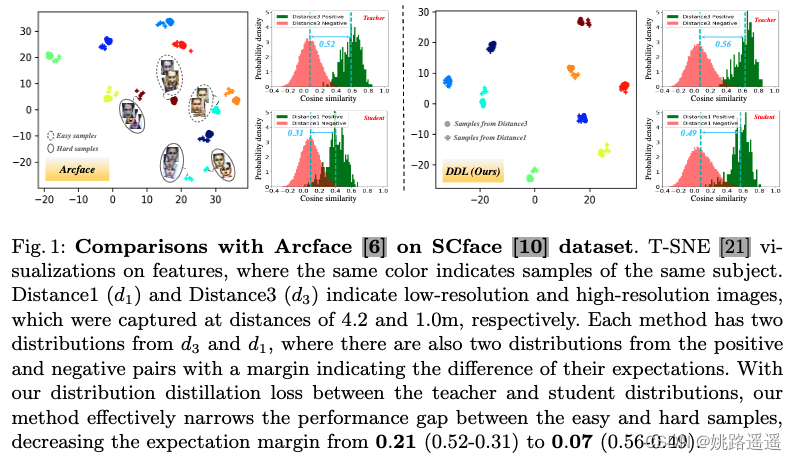
如图 1 所示,最先进的 (SotA) 面部分类器,如 Arcface [6],可以很好地处理特征空间中具有紧密分组的小变化图像。我们将这些表示为简单样本。相比之下,具有较大变化的图像通常与特征空间中的简单图像相距甚远,并且更难处理。我们将这些表示为困难样本。在图1中,相同的颜色表示同一主题的样本。 Distance1 (d1) 和 Distance3 (d3) 表示分别在 4.2 和 1.0m 的距离处捕获的低分辨率和高分辨率图像。 每种方法都有来自 d3 和 d1 的两个分布,其中也有来自正负对的两个分布,margin表示它们的期望差异。 通过我们在教师和学生分布之间的分布蒸馏损失,我们的方法有效地缩小了简单样本和困难样本之间的性能差距,将期望差从 0.21 (0.52-0.31) 降低到 0.07 (0.56-0.49)。
知识蒸馏相关:
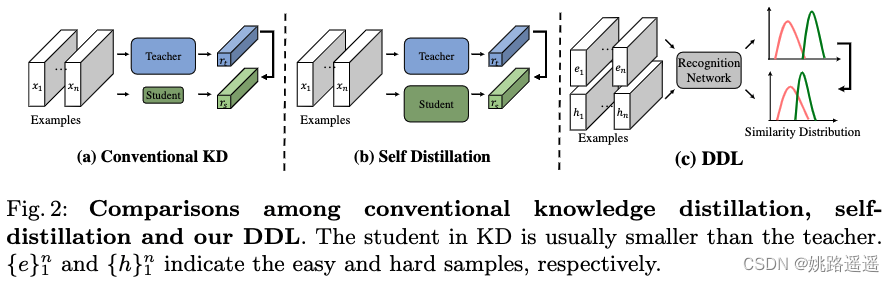
与传统蒸馏方法相比, DDL 在几个方面有所不同(见图 2):
- KD 至少有两个网络,一个老师和一个学生,而 DDL 只学习一个网络。 尽管在 KD中,学生可能具有与教师相同的结构(例如,自蒸馏),但他们在训练中具有不同的参数。
- KD使用sample-wise、Euclidean distance-wise或anglewise约束,而DDL提出了一种新的余弦相似度分布约束,专为人脸识别设计。
- 据我们所知,目前没有 KD 方法在人脸基准上优于 SotA 人脸分类器,而 DDL 始终优于 SotA Arcface 分类器。
2.DDL
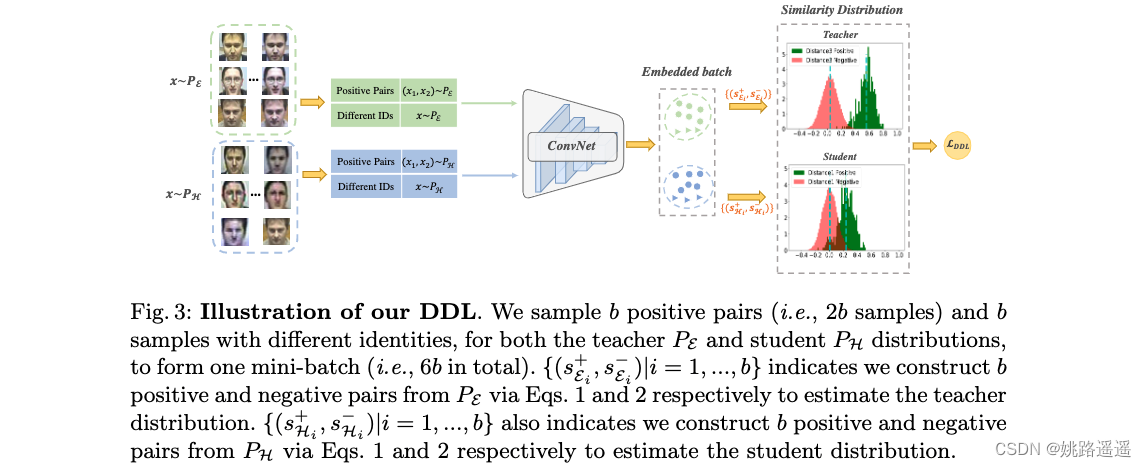
上图为 DDL 的框架。 我们将训练集分为两部分,即 E 表示简单样本,H 表示困难样本,分别形成教师和学生分布。 通常,对于训练期间的每个小批量,我们从两个部分进行采样。 为了确保良好的教师分布,我们使用 SotA FR 模型 [6] 作为我们的初始化。 提取的特征用于构建正负对(第 3.1 节),它们进一步用于估计相似性分布(第 3.2 节)。 最后,基于相似性分布,所提出的 DDL 用于训练分类器(第 3.3 节)。
2.1.Sampling Strategy from PE and PH
首先,我们介绍了在训练过程中如何在一个mini-batch中构建正负对的细节。 给定来自 PE 和 PH 的两种输入数据,每个 mini-batch 由四部分组成,两种正对(即 (x1, x2) ∼ PE 和 (x1, x2) ∼ PH),以及两种具有不同身份的样本(即 x∼PE 和 x∼PH)。 具体来说,我们一方面构造 b 个正对(即 2b 个样本),另一方面构造 b 个来自 PE 和 PH 不同身份的样本。 结果,每个 mini-batch 中有 6b = (2b + b) * 2 个样本(更多细节见图 3)。
2.1.1.Positive Pairs
正对是预先离线构建的,每对由两个具有相同身份的样本组成。 如图 3 所示,每个正对的样本按顺序排列。 通过深度网络F将数据嵌入到高维特征空间后,可以得到正对s+的相似度如下:
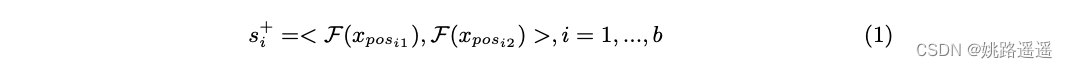
其中 xposi1 、 xposi2 是一对正样本。 请注意,相似度小于 0 的正对通常是异常值,由于我们的主要目标不是专门处理噪声,因此将其作为实际设置删除。
2.1.1.Negative Pairs
与正对不同,我们通过困难负样本挖掘从具有不同身份的样本在线构建负对,它选择具有最大相似性的负对。 具体来说,负对s−的相似度定义为:
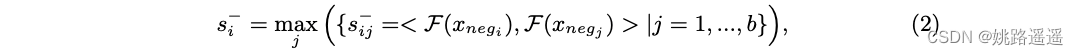
其中 xnegi , xnegj 来自不同的ID。 一旦构造了正负对的相似性,就可以估计相应的分布。
2.2.Similarity Distribution Estimation
相似性分布估计的过程类似于[37],它使用具有软分配的一维直方图以简单且分段可微分的方式执行。 具体来说,来自同一个人的两个样本xi,xj组成正对,对应的标签记为mij = +1。 相反,来自不同人的两个样本形成负对,标签表示为 mij = -1。 然后,我们得到两个样本集 S+ = {s+ = 〈F (xi), F (xj)〉|mij = +1} 和 S− = {s− = 〈F (xi), F (xj)〉|mij = −1} 分别对应于正负对的相似性。
令 p+ 和 p− 分别表示 S+ 和 S− 的两个概率分布。 与基于余弦距离的方法 [6] 一样,每对的相似性限制为 [−1, 1],这被证明可以简化任务 [37]。 受直方图损失的启发,我们通过用均匀间隔的 bin 拟合简单直方图来估计这种类型的一维分布。 我们采用 R 维直方图 H+ 和 H−,节点 t1 = −1, t2, … , tR = 1 均匀填充 [−1, 1],步长为 2 / R−1。 然后,我们估计直方图 H+ 在每个 bin 的值 h+r 为:
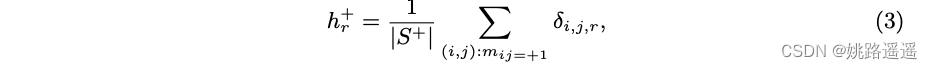
其中 (i, j) 跨越所有正对。 与 [37] 不同,权重 δi,j,r 由指数函数选择为:
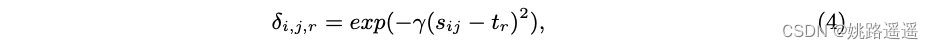
其中 γ 表示高斯核函数的扩展参数,tr 表示直方图的第 r 个节点。 我们采用高斯核函数,因为它是最常用的密度估计核函数,并且对小样本量具有鲁棒性。 H− 的估计类似地进行。
2.3.Distribution Distillation Loss
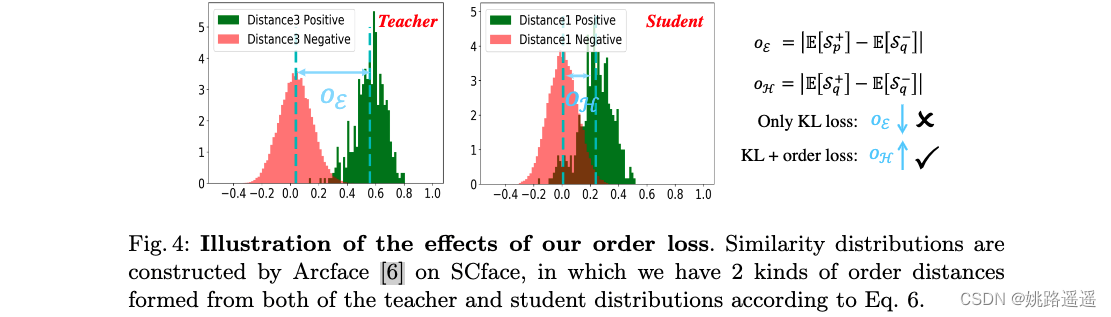
我们利用 [6] 等 SotA 人脸识别引擎,从两种样本中获取相似度分布:简单样本和困难样本。 这里,easy samples 表明 FR engine 表现良好,其中正负对的相似度分布明显分开(参见图 4 中的教师分布),而 hard samples 表明 FR engine 表现不佳,其中 相似性分布可能高度重叠(参见图 4 中的学生分布)。
2.3.1.KL Divergence Loss
为了缩小简单样本和困难样本之间的性能差距,我们将困难样本的相似性分布(即学生分布)约束为近似简单样本的相似性分布(即教师分布)。 教师分布由正对和负对的两个相似性分布组成,分别表示为 P + 和 P - 。 类似地,学生分布也由两个相似性分布组成,表示为 Q+ 和 Q−。 受先前 KD 方法 [12, 53] 的启发,我们采用 KL 散度来约束学生和教师分布之间的相似性,其定义如下(其中 λ1, λ2 是权重参数):
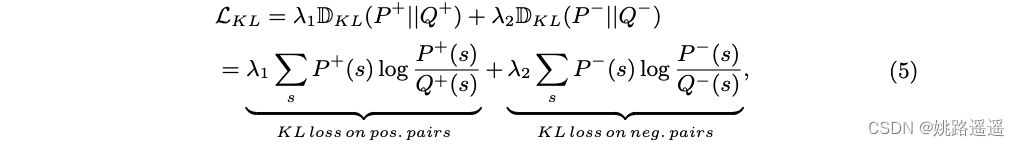
2.3.2.Order Loss
然而,仅使用 KL 损失并不能保证良好的性能。 事实上,教师分布可能会选择接近学生分布,并导致正对和负对分布之间出现更多混淆区域,这与我们的目标相反(见图 4)。 为了解决这个问题,我们设计了一个简单而有效的术语,称为 order loss,它最小化负对和正对的相似性分布期望之间的距离,以控制重叠。 我们的order loss可以表述如下:
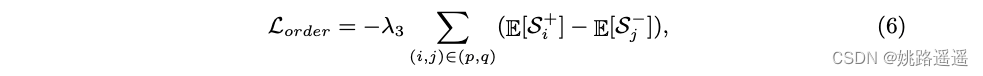
其中 S+ p 和 S− p 表示教师分布的正负对的相似度; S+ q 和 S− q 表示学生分布的正负对的相似度; λ3 是权重参数。
总之,我们的分布蒸馏损失的整个公式是:LDDL = LKL + Lorder。 DDL 可以很容易地扩展到多个学生分布,从一个特定的变体变化如下:
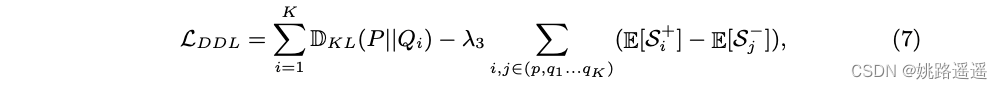
其中 K 是学生分布的数量。 此外,为了保持简单样本的性能,我们结合了 Arcface [6] 的损失函数,因此最终损失为:
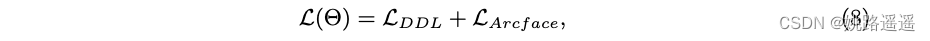
其中 Θ 表示参数集。 请注意,LArcface 可以很容易地替换为 FR 中任何一种流行的损失。
2.4.Generalization on Various Variations
接下来,我们讨论 DDL 在各种变体上的泛化,它定义了我们的应用场景以及我们如何选择简单/困难样本。 基本上,我们可以根据图像是否包含可能阻碍身份信息的大面部变化(例如,低分辨率和大姿势变化)来区分简单和困难样本。
2.4.1.Observation from Different Variations
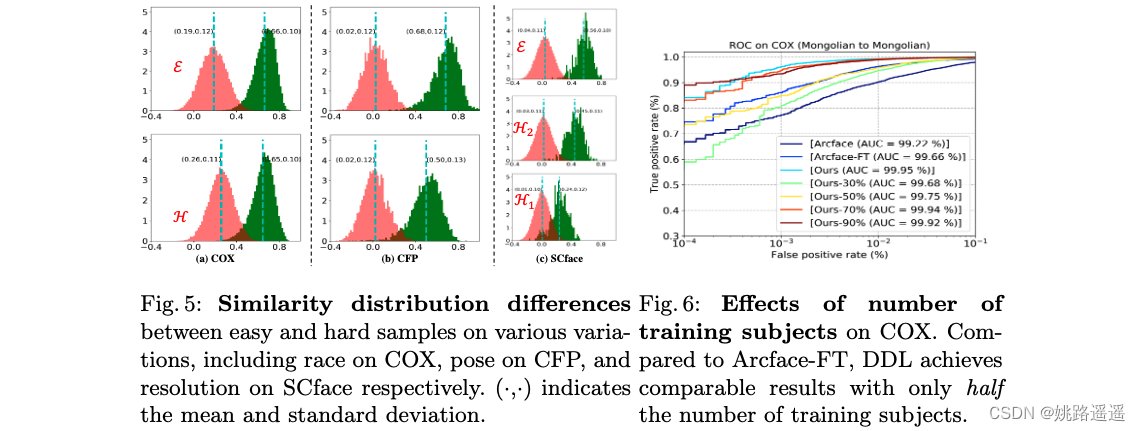
我们的方法假设两个或多个分布,每个分布都是从训练数据的一个子集计算出来的,它们之间存在差异,这是人脸识别中的一种普遍现象,如图 5 所示。它显示了正常和具有挑战性的样本的相似性分布基于 Arcface [6] 在 CASIA 上训练,除了 CFP,它在 VGGFace2 上训练。 正如我们所见,1)由于 CASIA 偏向高加索人,COX 中的蒙古样本更难,因此相对被视为困难样本,2)不同的变化有一个共同的观察结果,即具有挑战性的样本的相似性分布通常与那些样本不同简单样本的数量,3)不同程度的变化可能具有不同的相似性分布(例如,图 5(c)中的 H1 和 H2)。 总之,当一项任务满足简单样本和困难样本之间的相似性分布不同时,我们的方法是一个很好的解决方案,并且可以通过正确构建正负对来享受性能提升,如4.3节中所验证的那样。
2.4.2.Performance Balance Between Easy and Hard Samples
提高困难样本的性能同时保持简单样本的性能是一种权衡。 我们方法中的两个因素有助于保持简单样本的性能。 首先,我们结合了 SotA Arcface 损失 [6] 来保持简单样本的特征可辨别性。 其次,我们的order loss最小化了负对和正对的相似性分布期望之间的距离,这有助于控制正负对之间的重叠。
2.4.3.Discussions on Mixture Variations.
如公式(7)所示,我们的方法可以很容易地扩展到一项任务的多种变体(例如,低分辨率、大姿势等)。 另一种方法是将一项任务的不同程度的变化混合到一个学生分布中,如第 4.2 节所示、对不同程度的具体建模不够好,容易导致性能下降。 对于不同任务的不同变化,也可以构建多个师生分布对分别解决相应的任务,这不失为一个很好的未来方向。
相关文章:

【人脸识别】DDL:数据分布知识蒸馏思想,提升困难样本(遮挡、低分辨率等)识别效果
论文题目:《Improving Face Recognition from Hard Samples via Distribution Distillation Loss》 论文地址:https://arxiv.org/pdf/2002.03662v3.pdf 代码地址:https://github.com/HuangYG123/DDL 1.前言及相关工作 Large facial variatio…...
如何管理好仓库/库房?
仓库管理是企业管理中不可缺少的一部分,事关企业能否正常运行的关键之一,古人有云:“三军未动粮草先行”,一个企业仓库管理做不好,他的生产管理肯定也是做不好的,不是说生产管理人员的管理能力不具备&#…...

Unity Lighting -- Unity的光源简介
在主菜单栏中,点击Window -> Rendering -> Light Explorer打开光源管理器,这个标签页可以看到场景中所有的光源,包括每个光源的类型,形状,模式,颜色,强度,阴影等信息。 在主菜…...
Android仿网易云音乐歌单详情页
效果图实现思路:1、Activity设置自定义Shared Element切换动画2、透明状态栏(透明Toolbar,使背景图上移)3、Toolbar底部增加和背景一样的高斯模糊图,并上移图片(为了使背景图的底部作为Toolbar的背景)4、上…...

linux基本功系列之free命令实战
文章目录前言一. free命令介绍二. 语法格式及常用选项三. 参考案例3.1 查看free相关的信息3.2 以MB的形式显示内存的使用情况3.3 以总和的形式显示内存的使用情况3.4 周期性的查询内存的使用情况3.5 以更人性化的形式来查看内存的结果输出总结前言 大家好,又见面了…...

华为OD机试模拟题 用 C++ 实现 - 连续子串(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 最多获得的短信条数(2023.Q1)) 文章目录 最近更新的博客使用说明连续子串题目输入输出示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。 华为 OD …...
【软考——系统架构师】UML 建模与架构文档化
🔎这里是【软考——系统架构师】,关注我考试轻松过线 👍如果对你有帮助,给博主一个免费的点赞以示鼓励 欢迎各位🔎点赞👍评论收藏⭐️ 文章目录UML 基础UML 软件开发过程系统架构文档化送书福利UML 基础 U…...

Spring中常用注解
声明 bean 的注解 Component:泛指各种组件 Controller、Service、Repository 都可以称为Component Controller:控制层 Service:业务层 Repository:数据访问层Bean 的生命周期属性 Scope 设置类型包括:设置 Spring 容器…...
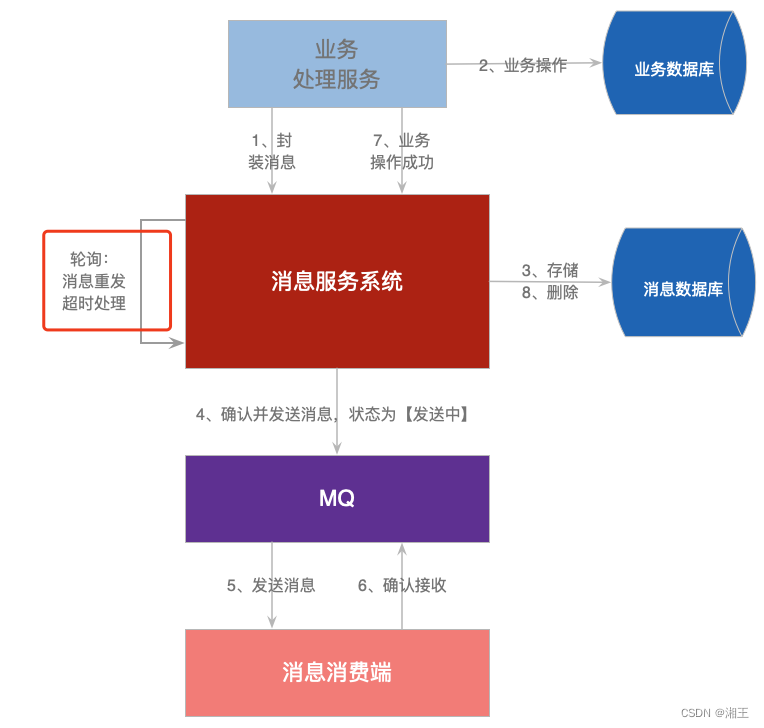
基于SpringCloud的可靠消息最终一致性06:轮询事务消息
上一节把可靠消息最终一致性的正常逻辑代码顺序执行了一次,并且对于同一个事务消息,在正常情况下它要被发送至少两次。 这是因为在发送消息之前,TransactionMessageService就已经把消息保存到了数据库中。而在首次消费完消息后,TransactionMessageListener并没有从数据库中…...

Python Flask + Echarts 轻松制作动态酷炫大屏( 附代码)
目录一、确定需求方案二、整体架构设计三、编码实现 (关键代码)四、完整代码五、运行效果1.动态实时更新数据效果图 说明: 其中 今日抓拍,抓拍总数,预警信息统计,监控点位统计图表 做了动态实时更新处理。 2.静态…...
:SourceMap讲解以及使用)
Wepack(1):SourceMap讲解以及使用
今天我们来讲讲定位源码的工具 Sourcemap , 我们先讲最简单的配置,之后才补充 sourcemap 的其他属性 Sourcemap 作用 可以在打包的代码直接对应相应源码 例如 vue2 , vue3可以把对应的错误上传到相关服务器 使用 webpack.config.js const config …...

华为OD机试题,用 Java 解【最多等和不相交连续子序列】问题
最近更新的博客 华为OD机试题,用 Java 解【停车场车辆统计】问题华为OD机试题,用 Java 解【字符串变换最小字符串】问题华为OD机试题,用 Java 解【计算最大乘积】问题华为OD机试题,用 Java 解【DNA 序列】问题华为OD机试 - 组成最大数(Java) | 机试题算法思路 【2023】使…...
Kubernetes06:Controller
Kubernetes06:Controller 1、什么是controller 管理和运行容器的对象,是一个物理概念 在集群上管理和运行容器的对象 2、Pod和Controller之间的关系 Pod是通过controller来实现应用的运维 比如伸缩、滚动升级等等操作Pod和Controller之间通过 label 标签建立关系…...

采购文件中 RFI、RFQ、RFP、IFB的区别
【PMBOK的描述】 采购文件用于征求潜在卖方的建议书。如果主要依据价格来选择卖方(如购买商业或标准产品时),通常就使用标书、投标或报价等术语。如果主要依据其他考虑(如技术能力或技术方法)来选择卖方࿰…...

linux升级gcc版本详细教程
0.前言一般linux操作系统默认的gcc版本都比较低,例如centos7系统默认的gcc版本为4.8.5。gcc是从4.7版本开始支持C11的,4.8版本对C11新特性的编译支持还不够完善,因此如果需要更好的体验C11以及以上版本的新特性,需要升级gcc到一个…...

NBA Top Shot 跌落神坛
近日,美国职业篮球联盟(NBA)授权的NFT 项目“NBA Top Shot Moments”被纽约法院初步裁定为“可能符合证券的定义”,虽然这不是对2021年用户指控该项目违法的最终判决,但这个裁定引发了市场担忧,部分NFT的地…...
)
状态管理Pinia使用详解(带你入门)
状态管理Pinia使用详解(带你从入门到入神) 序: 如果你之前使用过 vuex 进行状态管理的话,那么 pinia 就是一个类似的插件。它是最新一代的轻量级状态管理插件。你可以通过defineStore来简单创建一个存储管理。 与 vuex 相比,pinia 提…...
Linux系统基础命令(一)
一、图形界面和终端界面 图形界面:是指采用图形方式显示的计算机操作用户界面。 终端界面:是指黑底白字的命令行界面。 什么是tty呢? tty:终端设备的统称。 tty一词源于Teletypes,或者teletypewriters,…...
djvu批量转换为pdf的工具和djvu阅读器(附下载链接)
简介 DjVuToy是一款美观易用、功能强大的DjVu处理工具,DjVuToy官方版功能包括图像文件转DjVu,支持PDG、BMP、GIF等格式。转换的同时可以进行OCR,生成双层DjVu。可以插入、删除、移动、旋转多页DjVu中的页面。还可以将多个DjVu文件合并成一个&…...

Linux | 分布式版本控制工具Git【版本管理 + 远程仓库克隆】
文章目录一、前言二、有关git的相关历史介绍三、Git版本管理1、感性理解 —— 大学生实验报告2、程序员与产品经理3、张三的CEO之路 —— 版本管理工具的诞生四、如何在Linux上使用Git1、创建仓库2、将仓库克隆到本地3、git三板斧① git add② git commit③ git push4、有关git…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
