interview review
M:
- intrinsic matrix
[ f x s c x 0 f y c y 0 0 1 ] \begin{bmatrix}f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{bmatrix} fx00sfy0cxcy1
( c x , c y ) (c_x, c_y) (cx,cy): camera center in pixels
( f x , f y ) (f_x, f_y) (fx,fy): focal length in pixels
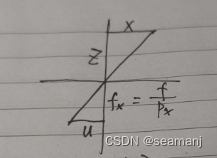
X Z = u f x \frac{X}{Z} = \frac{u}{f_x} ZX=fxu
其中 f x = f p x f_x = \frac{f}{p_x} fx=pxf, f f f 是focal length in world unites (millimeters), p x p_x px像素宽度, 通过胶片宽度除以像素X方向的个数得到.
下面来看skew
s = f x t a n α s = f_x tan \alpha s=fxtanα
假设每 p y p_y py在 p x p_x px上面的偏移是 b b b
那么 t a n α = b p x p y tan \alpha = \frac{bp_x}{p_y} tanα=pybpx
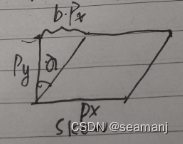
那么 [ f x s c x 0 f y c y 0 0 1 ] ∗ [ X Z Y Z 1 ] \begin{bmatrix}f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{bmatrix} *\begin{bmatrix} \frac{X}{Z} \\ \frac{Y}{Z} \\ 1 \end{bmatrix} fx00sfy0cxcy1 ∗ ZXZY1
第一行可得 f x ∗ X Z + s ∗ Y Z + c x = f x ∗ X Z + f x t a n α ∗ Y Z + c x f_x * \frac{X}{Z} +s * \frac{Y}{Z} + c_x = f_x * \frac{X}{Z} + f_x tan \alpha * \frac{Y}{Z} + c_x fx∗ZX+s∗ZY+cx=fx∗ZX+fxtanα∗ZY+cx
这里 f x t a n α ∗ Y Z f_x tan \alpha * \frac{Y}{Z} fxtanα∗ZY有两种理解方式, 第一种是通过 t a n α ∗ Y tan \alpha *Y tanα∗Y将在世界坐标系中将 Y Y Y转成 X X X方向的偏移 b X bX bX, 然后将这个偏移通过乘以 f x z \frac{f_x}{z} zfx转成x方向的像素偏移
第二种是 f x t a n α ∗ Y Z = f p x ∗ b p x p y ∗ Y Z = b f y ∗ Y Z f_x tan \alpha * \frac{Y}{Z} = \frac{f}{p_x}*\frac{bp_x}{p_y} * \frac{Y}{Z} = bf_y*\frac{Y}{Z} fxtanα∗ZY=pxf∗pybpx∗ZY=bfy∗ZY 先算在y方向有多少像素, 再乘以 b b b得到偏移
第二行注意如果有skew, 那么 f y f_y fy得用 f y c o s α \frac{f_y}{cos\alpha} cosαfy代替, 因为y轴变斜了, 相应也变长了
https://towardsdatascience.com/camera-calibration-fda5beb373c3
https://towardsdatascience.com/what-are-intrinsic-and-extrinsic-camera-parameters-in-computer-vision-7071b72fb8ec
相关文章:

interview review
M: intrinsic matrix [ f x s c x 0 f y c y 0 0 1 ] \begin{bmatrix}f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\end{bmatrix} fx00sfy0cxcy1 ( c x , c y ) (c_x, c_y) (cx,cy): camera center in pixels ( f x , f y …...

layui表头多出一列(已解决)
问题描述 :layui表头多出来一列,但是表体没有内容,很影响美观。 好像是原本的表格有滚轮,我操作放大之后滚轮没有了,但是滚轮自带的表头样式还在, 之后手动把这个样式隐藏掉了,代码如下…...

LeetCode解法汇总307. 区域和检索 - 数组可修改
目录链接: 力扣编程题-解法汇总_分享记录-CSDN博客 GitHub同步刷题项目: https://github.com/September26/java-algorithms 原题链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 描述: 给你一个数…...
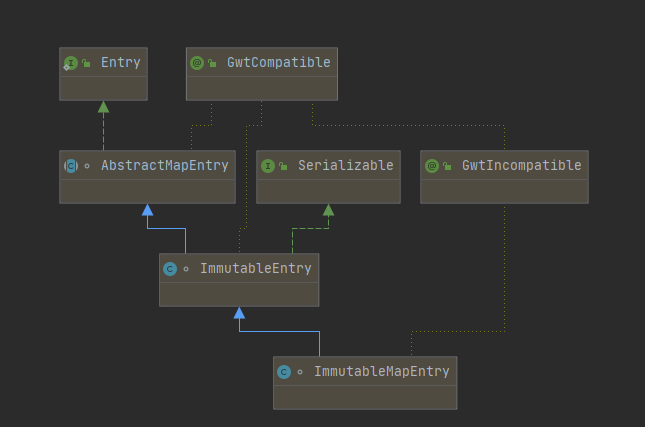
Java源码分析:Guava之不可变集合ImmutableMap的源码分析
原创/朱季谦 一、案例场景 遇到过这样的场景,在定义一个static修饰的Map时,使用了大量的put()方法赋值,就类似这样—— public static final Map<String,String> dayMap new HashMap<>(); static {dayMap.put("Monday&q…...
详解自动化测试之 Selenium
目录 1. 什么是自动化 2.自动化测试的分类 3. selenium(web 自动化测试工具) 1)选择 selenium 的原因 2)环境部署 3)什么是驱动? 4. 一个简单的自动化例子 5.selenium 常用方法 5.1 查找页面元素&…...
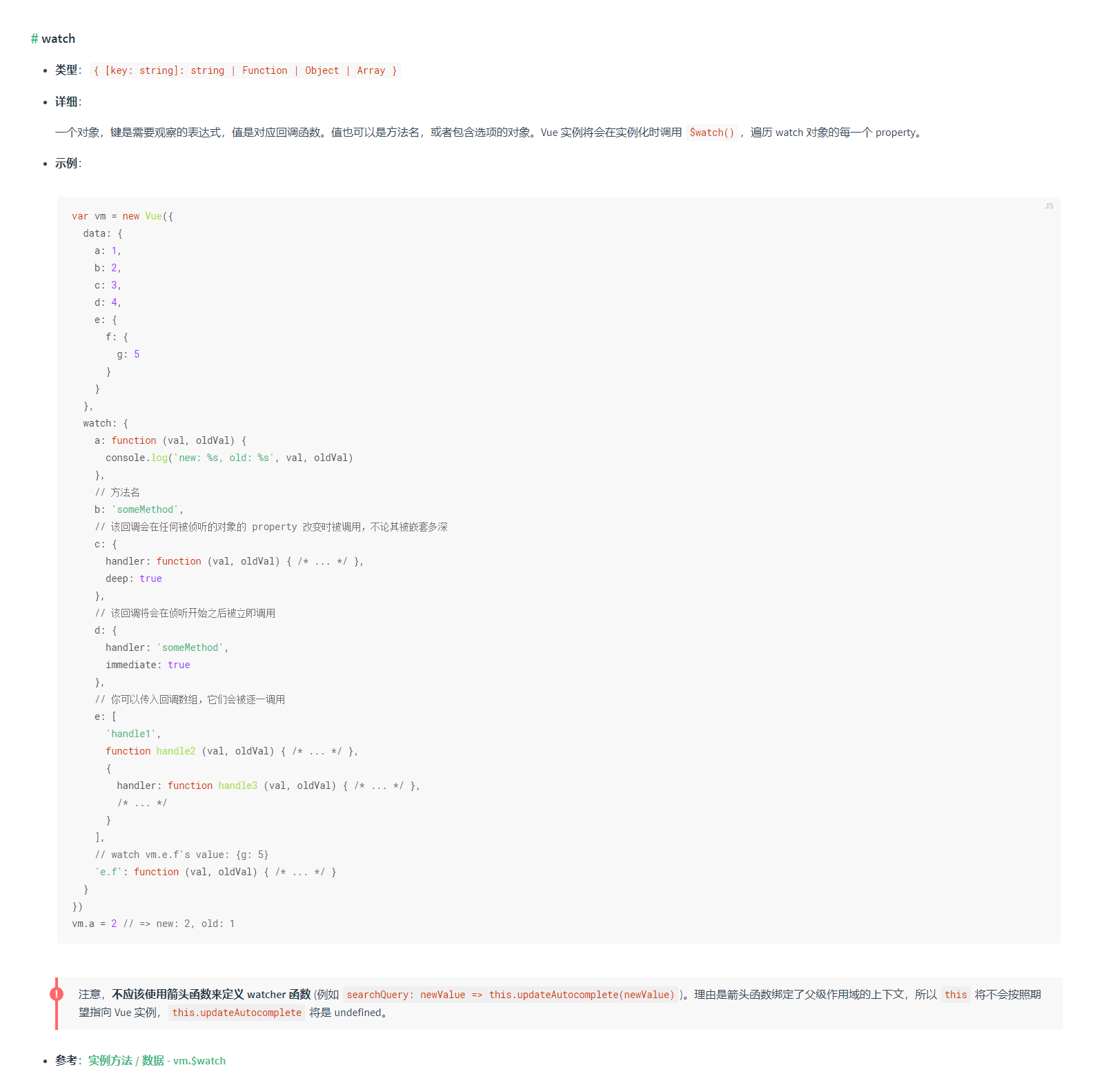
vue监听对象属性值变化
一、官方文档 二、实现方法 方法一、直接根据watch来监听 export default {data() {return {object: {username: ,password: }}},watch: {object.username(newVal, oldVal) {console.log(newVal, oldVal)}} }方法二:利用watch和computed来实现监听 利用computed定…...
)
Unicode编码的emoji表情如何在前端页面展示(未完成)
Unicode编码的emoji表情如何在前端页面展示 一、首先几个定义解决办法 一、首先几个定义 U1F601 和 0x1F601 表示同一个 Unicode 代码点,即笑脸 Emoji 的代码点。它们之间的区别在于表示方式和数据类型。 1.U1F601 是一种常见的表示方式,也称为 “U” 标…...
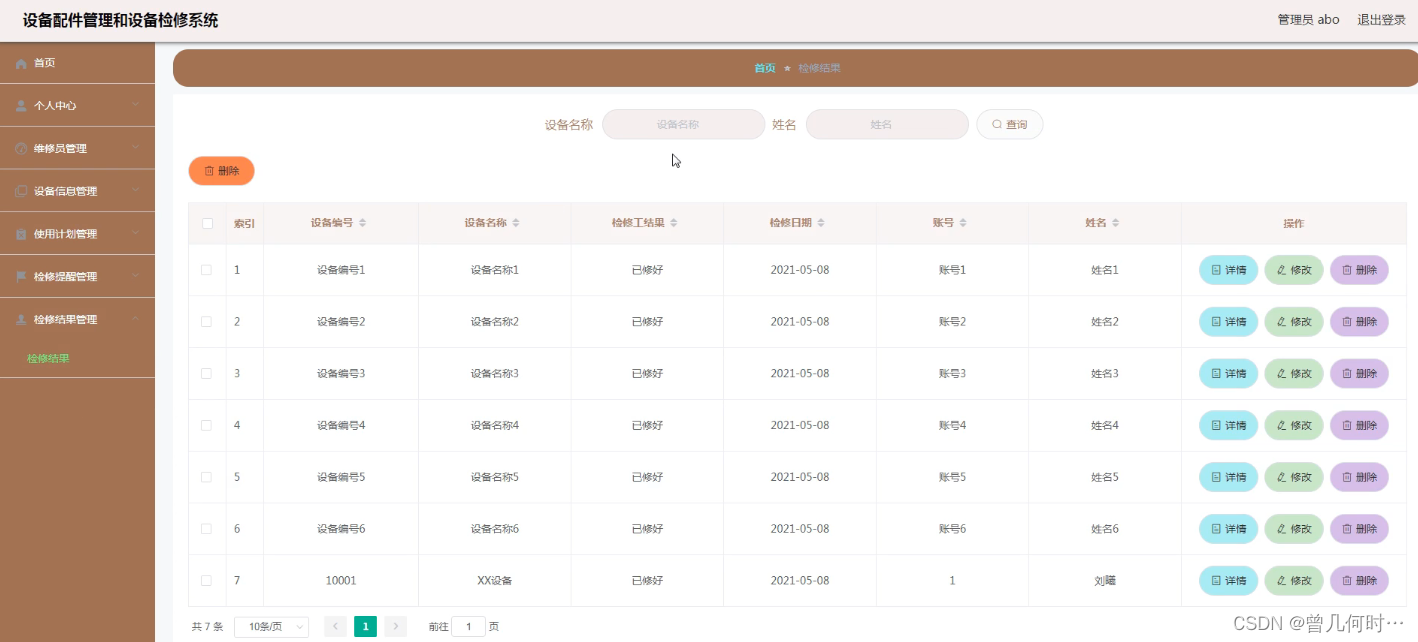
基于SSM的设备配件管理和设备检修系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...
鸿蒙开发|鸿蒙系统项目开发前的准备工作
文章目录 鸿蒙项目开发的基本流程介绍鸿蒙项目开发和其他项目有什么不同成为华为开发者-注册和实名认证1.登录官方网站 鸿蒙项目开发的基本流程介绍 直接上图,简单易懂! 整个项目的开发通过4个模块进行:开发准备、开发应用、运行调试测试和发…...
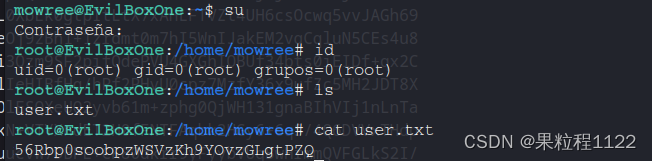
Evil靶场
Evil 1.主机发现 使用命令探测存活主机,80.139是kali的地址,所以靶机地址就是80.134 fping -gaq 192.168.80.0/242.端口扫描 开放80,22端口 nmap -Pn -sV -p- -A 192.168.80.1343.信息收集 访问web界面 路径扫描 gobuster dir -u http…...

第77题. 组合
原题链接:第77题. 组合 全代码: class Solution { private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() …...

读书笔记:彼得·德鲁克《认识管理》第21章 企业与政府
一、章节内容概述 企业社会责任最重要的维度之一是政企关系。无论对于企业的顺利运作,还是对于政府的顺利运作,政企关系都至关重要。然而,重商主义典范和宪政主义典范这两种传统理论越来越不适应社会现实,越来越失效。虽然当前尚…...

C/C++疫情集中隔离 2021年12月电子学会青少年软件编程(C/C++)等级考试一级真题答案解析
目录 C/C疫情集中隔离 一、题目要求 1、编程实现 2、输入输出 二、算法分析 三、程序编写 四、程序说明 五、运行结果 六、考点分析 C/C疫情集中隔离 2021年12月 C/C编程等级考试一级编程题 一、题目要求 1、编程实现 A同学12月初从国外回来,按照防疫要…...

052-第三代软件开发-系统监测
第三代软件开发-系统监测 文章目录 第三代软件开发-系统监测项目介绍系统监测 关键字: Qt、 Qml、 cpu、 内存、memory 项目介绍 欢迎来到我们的 QML & C 项目!这个项目结合了 QML(Qt Meta-Object Language)和 C 的强大功…...

向量矩阵范数pytorch
向量矩阵范数pytorch 矩阵按照某个维度求和(dim就是shape数组的下标)1. torch1.1 Tensors一些常用函数 一些安装问题cd进不去不去目录PyTorch里面_表示重写内容 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值 范数是向量或…...
NVIDIA Jetson OTA升级
从 JetPack 4.4 开始,可以使用包管理工具升级到下一个 JetPack 版本。请按照以下步骤执行升级。 1,小版本升级 (如,从 JetPack 4.4 升级到 JetPack 4.4.1) 第一步: sudo apt update 第二步: apt list --upgradable 第三步: sudo apt upgrade更新完之后重新启动即可 …...

【算法】算法题-20231118
这里写目录标题 一、16.17. 连续数列二、合并两个有序数组(力扣88)三、存在重复元素(217)四、有效的字母异位词(242) 一、16.17. 连续数列 简单 给定一个整数数组,找出总和最大的连续数列&…...
某60区块链安全之整数溢出漏洞实战学习记录
区块链安全 文章目录 区块链安全整数溢出漏洞实战实验目的实验环境实验工具实验原理攻击过程分析合约源代码漏洞EXP利用 整数溢出漏洞实战 实验目的 学会使用python3的web3模块 学会以太坊整数溢出漏洞分析及利用 实验环境 Ubuntu18.04操作机 实验工具 python3 实验原理…...
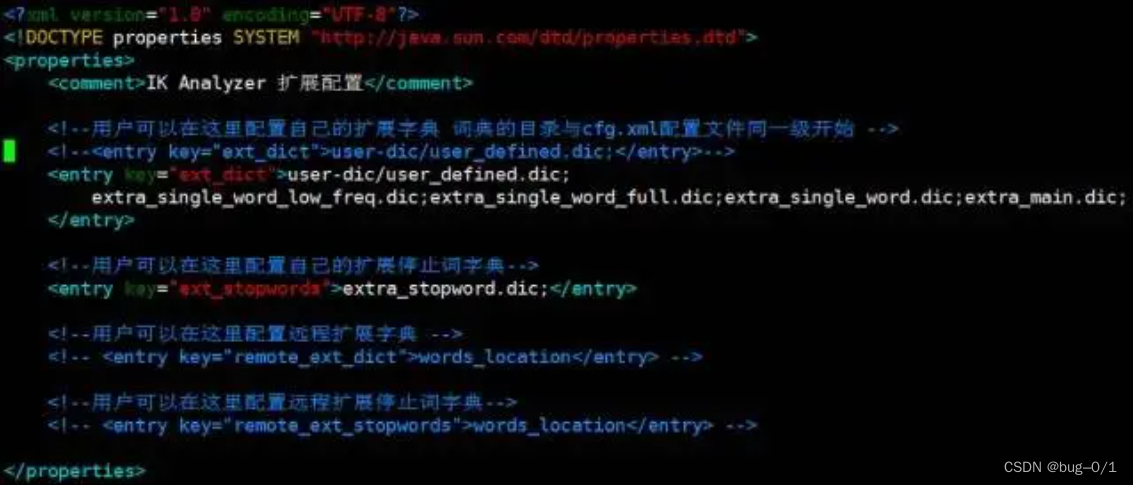
图数据库Neo4J 中文分词查询及全文检索(建立全文索引)
Neo4j的全文索引是基于Lucene实现的,但是Lucene默认情况下只提供了基于英文的分词器,下篇文章我们在讨论中文分词器(IK)的引用,本篇默认基于英文分词来做。我们前边文章就举例说明过,比如我要搜索苹果公司&…...

element-china-area-data使用问题
使用CodeToText报错,下载的时候默认下载最新版本的, 稳定版本5.0.2版本才可以 npm install element-china-area-data5.0.2 -S...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
