几种常用的排序
int[] arr = new int[]{1, 2,8, 7, 5};这是提前准备好的数组
- 冒泡排序
public static void bubbleSort(int[] arr) {int len = arr.length;for (int i = 0; i < len - 1; i++) {for (int j = 0; j < len - i - 1; j++) {if (arr[j] > arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}
- 选择排序
public static void selectionSort(int[] arr) {int len = arr.length;for (int i = 0; i < len - 1; i++) {int minIndex = i;for (int j = i + 1; j < len; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}if (minIndex != i) {int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}}
}
- 插入排序
public static void insertionSort(int[] arr) {int len = arr.length;for (int i = 1; i < len; i++) {int cur = arr[i];int j = i - 1;while (j >= 0 && arr[j] > cur) {arr[j+1] = arr[j]; j--;}arr[j+1] = cur;}
}
- 快速排序
public static void quickSort(int[] arr, int left, int right) {if (left >= right) {return;}int pivot = arr[right];int i = left, j = right - 1;while (i <= j) {while (i <= j && arr[i] < pivot) {i++;}while (i <= j && arr[j] >= pivot) {j--;}if (i < j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}} arr[right] = arr[i];arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);
}
- 归并排序
public static void mergeSort(int[] arr, int left, int right) {if (left >= right) {return;}int mid = left + (right - left) / 2;mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);merge(arr, left, mid, right);
}
private static void merge(int[] arr, int left, int mid, int right) {int[] temp = new int[right - left + 1];int i = left, j = mid + 1;int k = 0;while (i <= mid && j <= right) {if (arr[i] <= arr[j]) {temp[k++] = arr[i++];} else {temp[k++] = arr[j++];}}while (i <= mid) {temp[k++] = arr[i++];}while (j <= right) {temp[k++] = arr[j++];}for (int p = 0; p < temp.length; p++) {arr[left + p] = temp[p];}
}
这些排序算法的时间复杂度从O(n^2)到O(nlogn)不等,其中冒泡排序和选择排序为O(n^2),插入排序和归并排序为O(nlogn),快速排序的时间复杂度为O(nlogn)。
相关文章:

几种常用的排序
int[] arr new int[]{1, 2,8, 7, 5};这是提前准备好的数组 冒泡排序 public static void bubbleSort(int[] arr) {int len arr.length;for (int i 0; i < len - 1; i) {for (int j 0; j < len - i - 1; j) {if (arr[j] > arr[j1]) {int temp arr[j];arr[j] ar…...

性能测试【第三篇】Jmeter的使用
线程数:10 ,设置10个并发 Ramp-Up时间(秒):所有线程在多少时间内启动,如果设置5,那么每秒启动2个线程 循环次数:请求的重复次数,如果勾选"永远"将一直发送请求 持续时间时间:设置场景运行的时间 启动延迟:设置场景延迟启动时间 响应断言 响应断言模式匹配规则 包括…...

业务:业务系统检查项参考
名录明细云平台摸底1.原有云平台体系:VMware、openstack、ovirt、k8s、docker、混合云系列及版本 2.原有云平台规模,物理机数量、虚拟机数量、迁移业务系统所占配额 3.待补充系统摸底 (适用于物理主机)每一台虚拟机或物理机: 1.系统全局参数…...
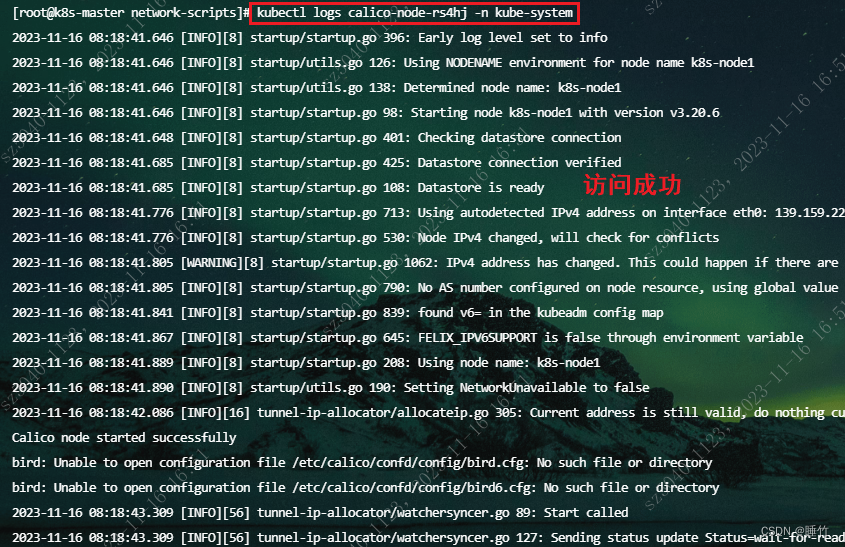
解决公网下,k8s calico master节点无法访问node节点创建的pod
目的:解决pod部署成功后,只能在node节点访问,而master节点无法访问 原因:集群搭建时,没有配置公网进行kubectl操作,从而导致系统默认node节点,使用内网IP加入k8s集群!如下ÿ…...

六边形架构
Alistair Cockburn是于1953年出生在美国的一位软件开发方法学家。他毕业于康奈尔大学计算机科学专业,并获得了博士学位。 Cockburn在敏捷软件开发领域做出了许多重要的贡献,他被广泛认可为敏捷方法学的奠基人之一。他提出了许多关于敏捷开发的原则和实践…...

基于单片机的智能家居安保系统(论文+源码)
1.系统设计 本次基于单片机的智能家居安保系统设计,在功能上如下: 1)以51单片机为系统控制核心; 2)温度传感器、人体红外静释电、烟雾传感器来实现检测目的; 3)以GSM模块辅以按键来实现远/近程…...
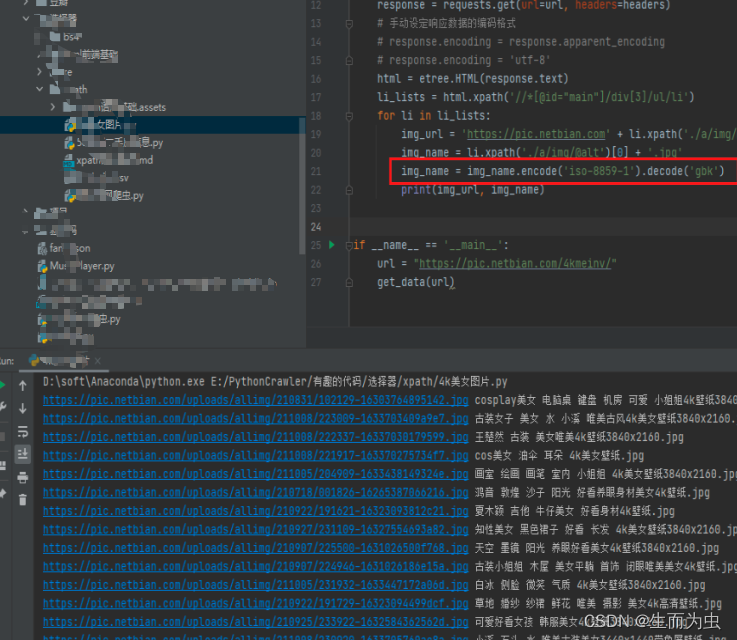
盘点3种Python网络爬虫过程中的中文乱码的处理方法
网络爬虫过程中三种中文乱码的处理方案,希望对大家的学习有所帮助 一、思路 其实解决问题的关键点就是在于一点,就是将乱码的部分进行处理,而处理的方案主要可以从两个方面进行出发。其一是针对整体网页进行提前编码,其二是针对…...

小程序富文本图片大小问题
文章目录 概要uniapp小程序情况解决方法及完整示例 概要 在小程序使用富文本或者在nuiapp(小程序的)使用富文本都会转为 <rich-text nodes"<p class"p class">内容</p>”></rich-text>如果是这种情况的话在css…...
Diagrams——制作短小精悍的流程图
今天为大家分享的是一款轻量级的流程图绘制软件——Diagrams。 以特定的图形符号加上说明,表示算法的图,称为流程图或框图。流程图是流经一个系统的信息流、观点流或部件流的图形代表。我们常用流程图来说明某一过程。 流程图使用一些标准符号代表某些类…...
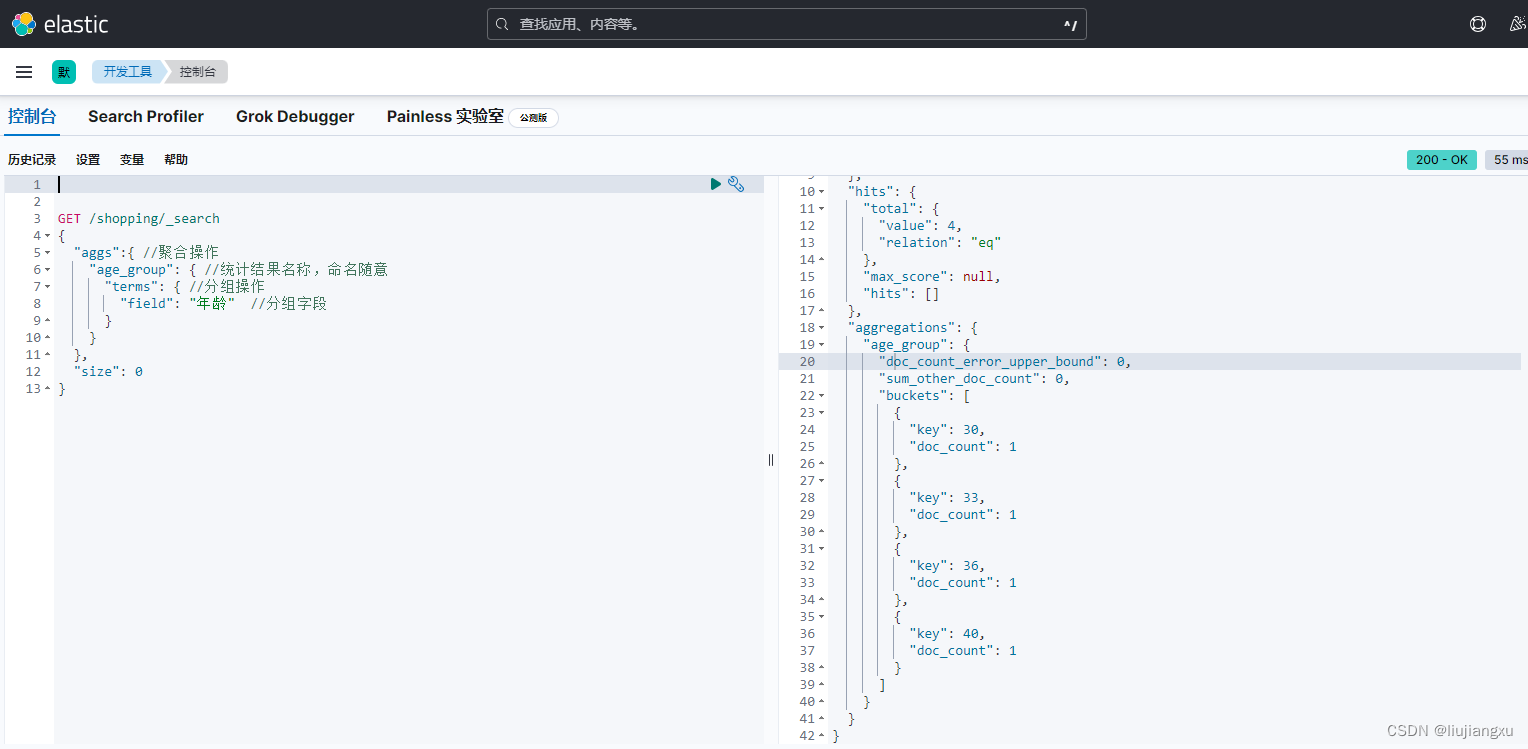
Elasticsearch基础条件查询
条件查询 query:查询 match:匹配 match_all:匹配所有 #第一种 GET /shopping/_search?q名字:张三#第二种 GET /shopping/_search {"query": {"match": {"名字": "张三"}} }#全量查询 match_all G…...

【SAP-ABAP】SAP与外围系统对接方式
SAP作为接受方 1.JAVA直接配置IP、账号、密码(有些人叫SAPWEBAPI)调用SAP里面的RFC函数 2.SAP发布RFC函数,配置webservice地址 3.SAP发布ODATA服务 4.SAP发布restful的http服务 5.我不太懂的UI5和FIORI本质好像也是odata服务 6.IDOC SA…...

云计算的发展趋势
云计算的发展一直是一个极具活力和创新的领域。随着技术的不断进步和应用场景的拓展,云计算将在未来继续发挥重要作用。以下是云计算发展的一些趋势: 边缘计算的崛起: 随着物联网设备的普及和应用场景的增多,边缘计算成为一个重要…...
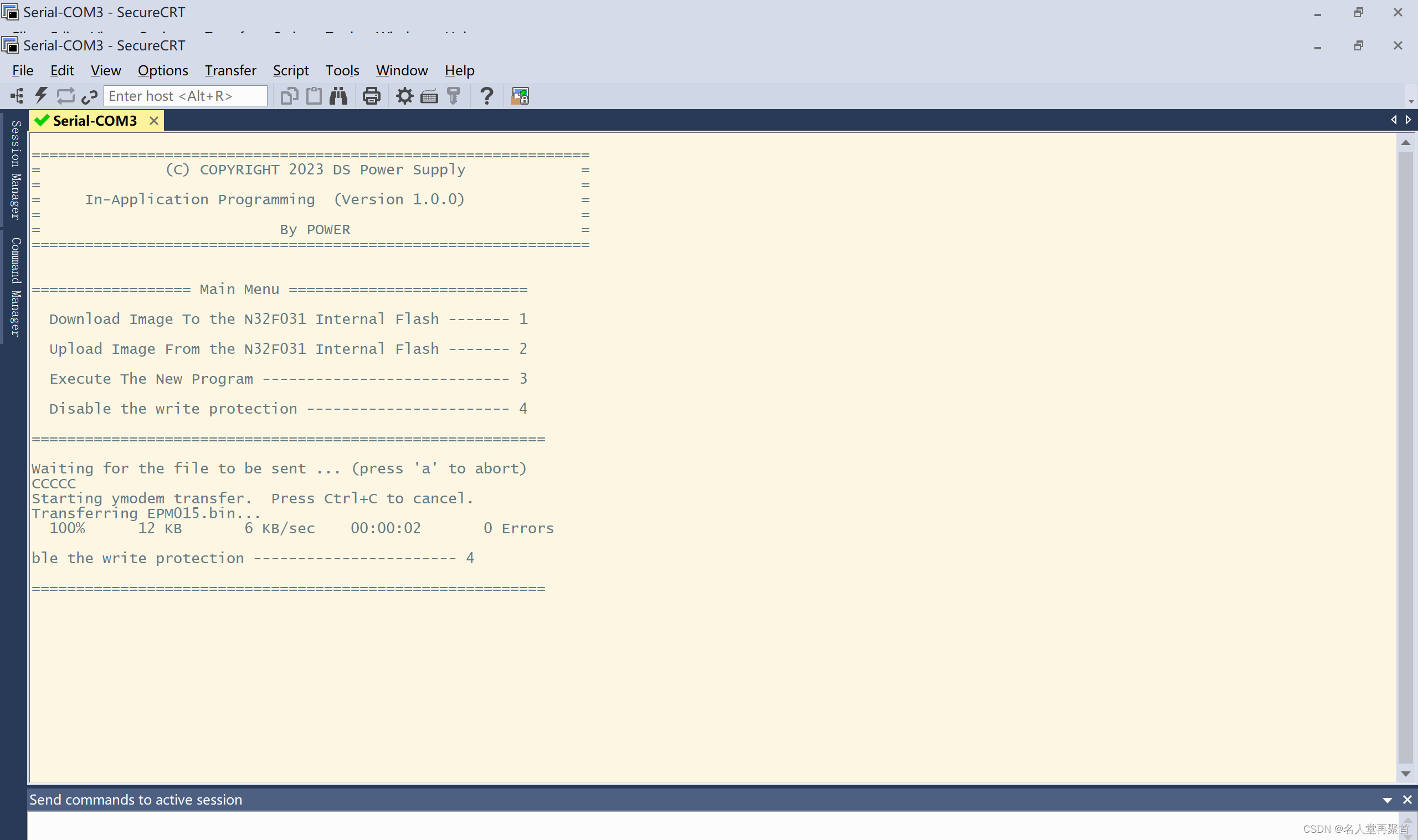
国民技术Cortex-M0系列单片机IAP升级
考虑到设备部署到现场后有可能需要进行软件升级,之前做过PIC系列单片机的升级,现在想做个国民技术N32G031系列Cortex-M0内核的单片机IAP方案。 因为国民技术系列单片机在很多大程度上都模仿了STM32,所以我想其升级方案极有可能差不多。于是在…...
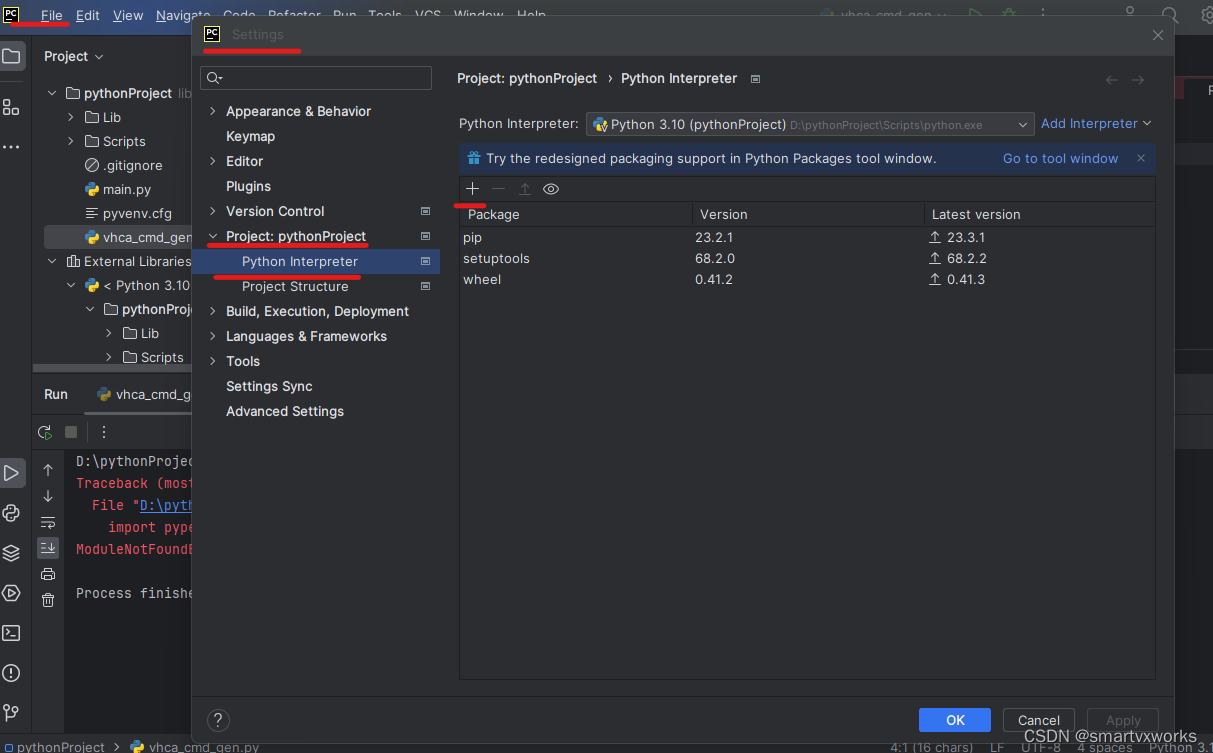
Pycharm中添加Python库指南
一、介绍 Pycharm是一款为Python开发者提供的集成开发环境(IDE),支持执行、调试Python代码,并提供了许多有用的工具和功能,其中之一就是在Pycharm中添加Python库。 添加Python库有许多好处,比如能够增加开…...

Oracle OCP / MySQL OCP认证容易通过吗
诸多学员在首次考OCP时,不清楚要如何选择。在本文中,我会为大家进行讲解! 选择OCP认证时需要考虑的几大项目: 授课老师师资经验 课程大纲 试听课程 考试通过率 业界口碑 服务质量 郭一军老师的OCP培训在业界培训的学员中已…...

flutter web 中嵌入一个html
介绍 flutter web 支持使用 HtmlElementView嵌入html import dart:html; import dart:ui as ui; import package:flutter/cupertino.dart;class WebWidget extends StatelessWidget {const WebWidget({super.key});overrideWidget build(BuildContext context) {DivElement fr…...

使用Spark SQL读取阿里云OSS的数据
读OSS数据 创建一个table,并关联OSS目录路径 CREATE TABLE my_table USING parquet OPTIONS (path oss://my_bucket/my_data_dir/dt20230904, -- 关联OSS路径header true, -- 如果Parquet文件包含列名的头部信息,则设置为true,否则设置为f…...
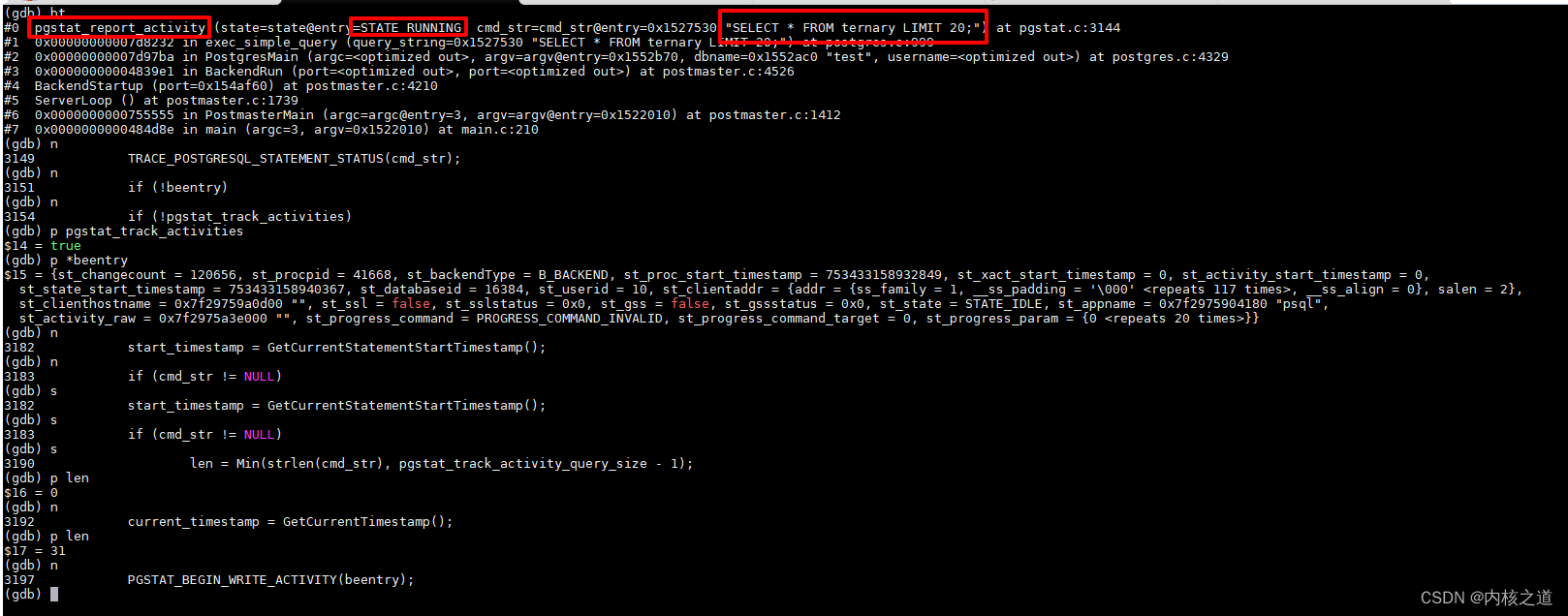
【0235】修改私有内存(private memory)中的MyBEEntry时,st_changecount值前后变化
上一篇: 【0234】PgBackendStatus 记录当前postgres进程的活动状态 1. pg_stat_activity中xxx实时信息如何实现? 客户端(eg:psql)在连接上postmaster之后,postmaster守护进程会fork()一个后端进场(backend process),之后此客户端的所有操作、交互均有此对应的Backen…...

Linux学习命令之source
在Linux中,source命令用于在当前shell环境中执行指定脚本文件中的命令。它通常用于重新加载修改过的shell配置文件,例如.bashrc或.profile,以使更改生效,而不需要退出当前的shell会话。 使用方法为: source 文件路径…...

2342. 数位和相等数对的最大和
我的解法: 对数组进行排序,最大数一定最先进入哈希表进行加和 class Solution { public:int maximumSum(vector<int>& nums) {unordered_map<int, vector<int>> h;int ans -1;sort(nums.begin(), nums.end());for (int i nums.…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
