【算法-哈希表3】四数相加2 和 赎金信
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正!
理论基础点这里
1. 四数相加2
分析题意
求符合条件的四元组的出现次数,条件:
- nums1
- nums2
- nums3
- nums4
从四个数组中的每一个数组取一个数 num1, num2, num3, num4,满足num1 + num2 + num3 + num4 == 0,则这是一个满足条件的四元组,可以记上它的出现次数。
题意转化
可以简单转化为 直接遍历取得4个数, 判断是否满足条件.但太慢,时间复杂度O(n^4)。
其实可以动动脑筋,将题意转化为 是否存在 两个两数之和 sum1 和 sum2 相加为0。
解决思路
四个数组该怎样去遍历,建立映射?
我们可以先遍历前两个数组,将数组中的元素两两求和得到sum1,把sum1和其出现次数建立映射得到哈希表sums1。接着遍历后两个数组,也两两求和得到sum2,在sums1中O(1)查找是否有一个和,和当前sum相加为0。
但为什么要这样遍历,我先遍历一个建立映射,再遍历三个不行吗?
这样我们在最终搜索比对的时候需要3层for来玩儿,那就是O(n^3)。而我们两两遍历只需要O(2 * n^2),这才是更好的。
编程实现
class Solution {
public:// 四数之和的判断 拆分为 两数之和的判断// 先遍历两个数组并求得所有两数之和sums1, 再遍历两个数组求剩下的两数之和, 查找是否有sum1 = -sum2int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {unordered_map<int, int> sums1; // <sum1, cnt> -- 题目不要求返回下标, 只用返回次数int sum1 = 0;int sum2 = 0;// 先遍历两个数组并求得所有两数之和sums1for (int &num1 : nums1) {for (int &num2 : nums2) {sum1 = num1 + num2;++sums1[sum1];}}// 再遍历两个数组求剩下的两数之和, 查找是否有sum1 = -sum2int cnt = 0;for (int &num3 : nums3) {for (int &num4 : nums4) {sum2 = num3 + num4;auto iter = sums1.find(-sum2);if (iter != sums1.end()) cnt += iter->second;}}return cnt;}
};
时间复杂度:O(n^2)
2. 赎金信
分析题意
“给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。”
题意转化
判断ransomNote的组成字符是否全部都在magazine中有足够的字符与之对应。
解决思路
查找,上哈希。遍历magazine,用哈希表描述magazine中的字符出现过多少次。
编程实现
class Solution {
public:bool canConstruct(string ransomNote, string magazine) {int appeared[26] = {0};// 用哈希表(数组)描述magazine中的哪些字符出现过.for (char &ch : magazine) ++appeared[ch - 'a'];// 在magazine中查找ransomNote的所有字符, 所有都能找到才是赎金信.for (char &ch : ransomNote) {--appeared[ch - 'a'];if (appeared[ch - 'a'] < 0) return false; // magazine中没有足够字符构成ransomNote}return true;}
};
时间复杂度:O(n)
空间复杂度:O(1)
今天的分享就到这里了,感谢您能看到这里。
这里是培根的blog,期待与你共同进步!
相关文章:

【算法-哈希表3】四数相加2 和 赎金信
今天,带来哈希表相关算法的讲解。文中不足错漏之处望请斧正! 理论基础点这里 1. 四数相加2 分析题意 求符合条件的四元组的出现次数,条件: nums1nums2nums3nums4 从四个数组中的每一个数组取一个数 num1, num2, num3, num4&am…...
wpf devexpress自定义编辑器
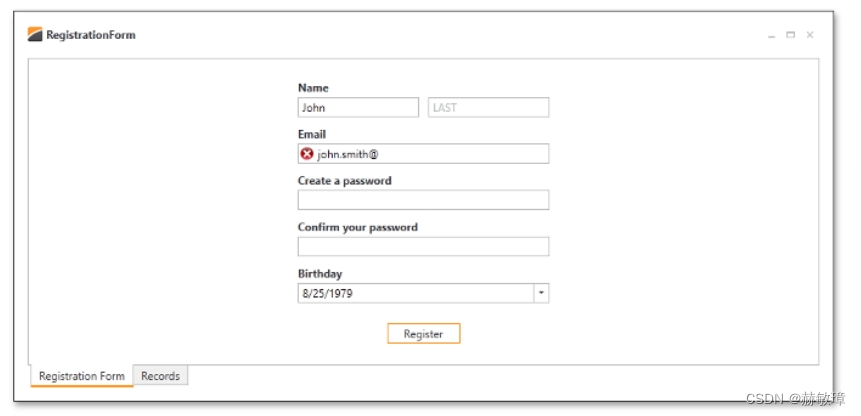
打开前一个例子 步骤1-自定义FirstName和LastName编辑器字段 如果运行程序,会通知编辑器是空。对于例子,这两个未命名编辑器在第一个LayoutItem(Name)。和最终用户有一个访客左右编辑器查阅到First Name和Last Name字段,分别。如果你看到Go…...
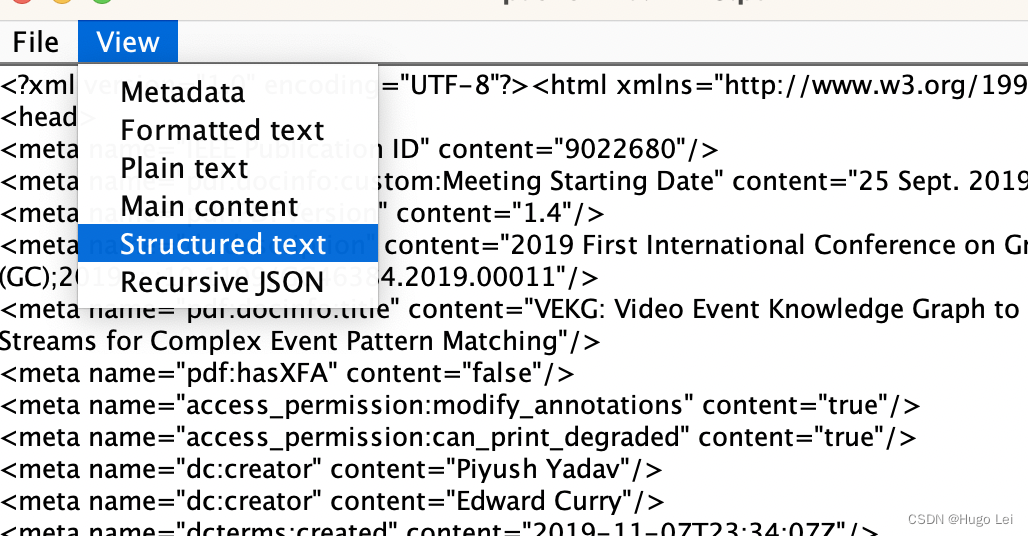
文档向量化工具(一):Apache Tika介绍
Apache Tika是什么?能干什么? Apache Tika是一个内容分析工具包。 该工具包可以从一千多种不同的文件类型(如PPT、XLS和PDF)中检测并提取元数据和文本。 所有这些文件类型都可以通过同一个接口进行解析,这使得Tika在…...

学习c#的第二十一天
目录 C# 泛型(Generic) 泛型类型参数 类型参数的约束 约束多个参数 未绑定的类型参数 类型参数作为约束 notnull 约束 class 约束 default 约束 非托管约束 委托约束 枚举约束 类型参数实现声明的接口 泛型类 泛型方法 泛型和数组 泛型…...

Michael Jordan最新报告:去中心化机器学习中的契约、不确定性和激励
导读 11月3日,智源研究院学术顾问委员会委员、机器学习泰斗Michael Jordan在以“新一代人工智能前沿”为主题的2023北京论坛 新工科专题论坛上,发表了题为Contracts, Uncertainty, and Incentives in Decentralized Machine Learning(去…...

3ds Max渲染用专业显卡还是游戏显卡?
使用3dsmax建模时,会面临诸多选择,除了用vr还是cr的决策,硬件选择上也存在着疑问,比如用专业显卡还是消费级游戏显卡?一般来说,除非是特别专业的大型项目和软件,且预算在5位数以上,常…...
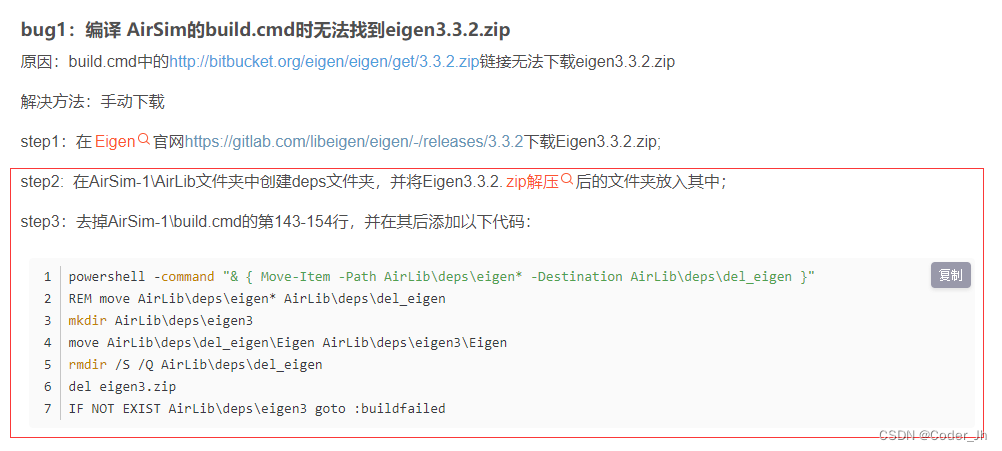
airlearning-ue4安装的踩坑记录
最近要安装airlearning-ue4,用于实现无人机仿真环境,该项目地址为:GitHub - harvard-edge/airlearning-ue4: Environment Generator for Air Learning Project. This version is build on top of UE4 game engine 由于这个项目已经完成好几年…...
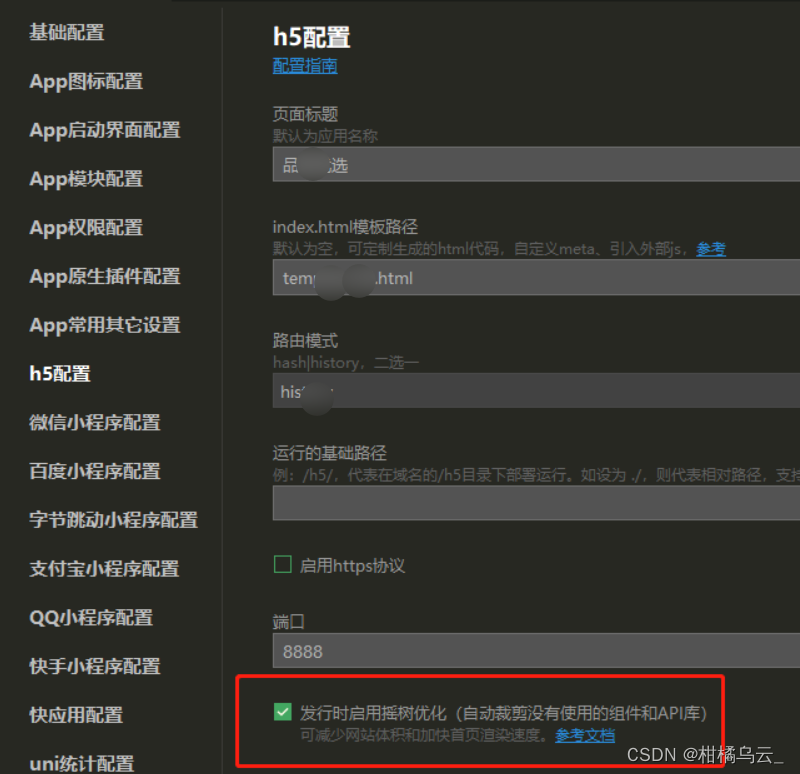
uniapp优化h5项目-摇树优化,gzip压缩和删除console.log
1.摇树优化 勾选摇树优化,打包删除死代码 2.gzip压缩和删除console.log 安装插件webpack和compression-webpack-plugin webpack插件 npm install webpack4.46.0 --save-devcompression-webpack-plugin插件 npm install compression-webpack-plugin6.1.1 --save-devconst Com…...

Pycharm之配置python虚拟环境
最近给身边的人写了脚本,在自己电脑可以正常运行。分享给我身边的人,却运行不起来,然后把报错的截图给我看了,所以难道不会利用pycharm搭建虚拟的环境?记录一下配置的过程。 第一步:右键要打开的python的代…...

如何使用MybatisPlus进行数据分页显示
如何使用MybatisPlus进行数据的分页呢? 使用Mybatis Plus提供的分页插件来简化开发,在MybatisPlusInterceptor的拦截器中添加自动分页的PaginationInnerInterceptor拦截器,当前配置需要交给spring的bean管理,类上添加注解Configu…...

代码随想录 Day49 单调栈01 LeetCode LeetCodeT739每日温度 T496 下一个最大元素I
前言 折磨的死去活来的动态规划终于结束啦,今天秋秋给大家带来两题非常经典的单调栈问题,可能你不清楚单调栈是什么,可以用来解决什么问题,今天我们就来一步一步的逐渐了解单调栈,到能够灵活使用单调栈.注意以下讲解中,顺序的描述为 从栈头到栈底的顺序 什么时候用单…...
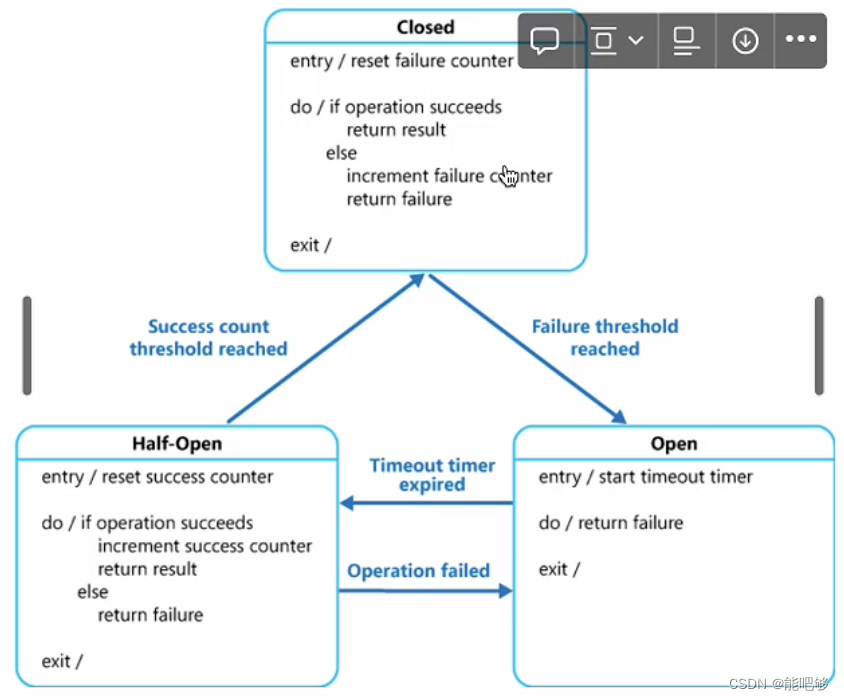
高可用--限流熔断降级
熔断 熔断是应对微服务雪崩效应的一种链路保护机制。 场景 服务端出现问题 服务指标:响应时间、错误率、连续错误数等,超过阈值出发熔断。硬件指标:CPU、网络IO、内存 目的 服务端恢复需要时间、服务端需要休息避免全调用链路崩溃&…...
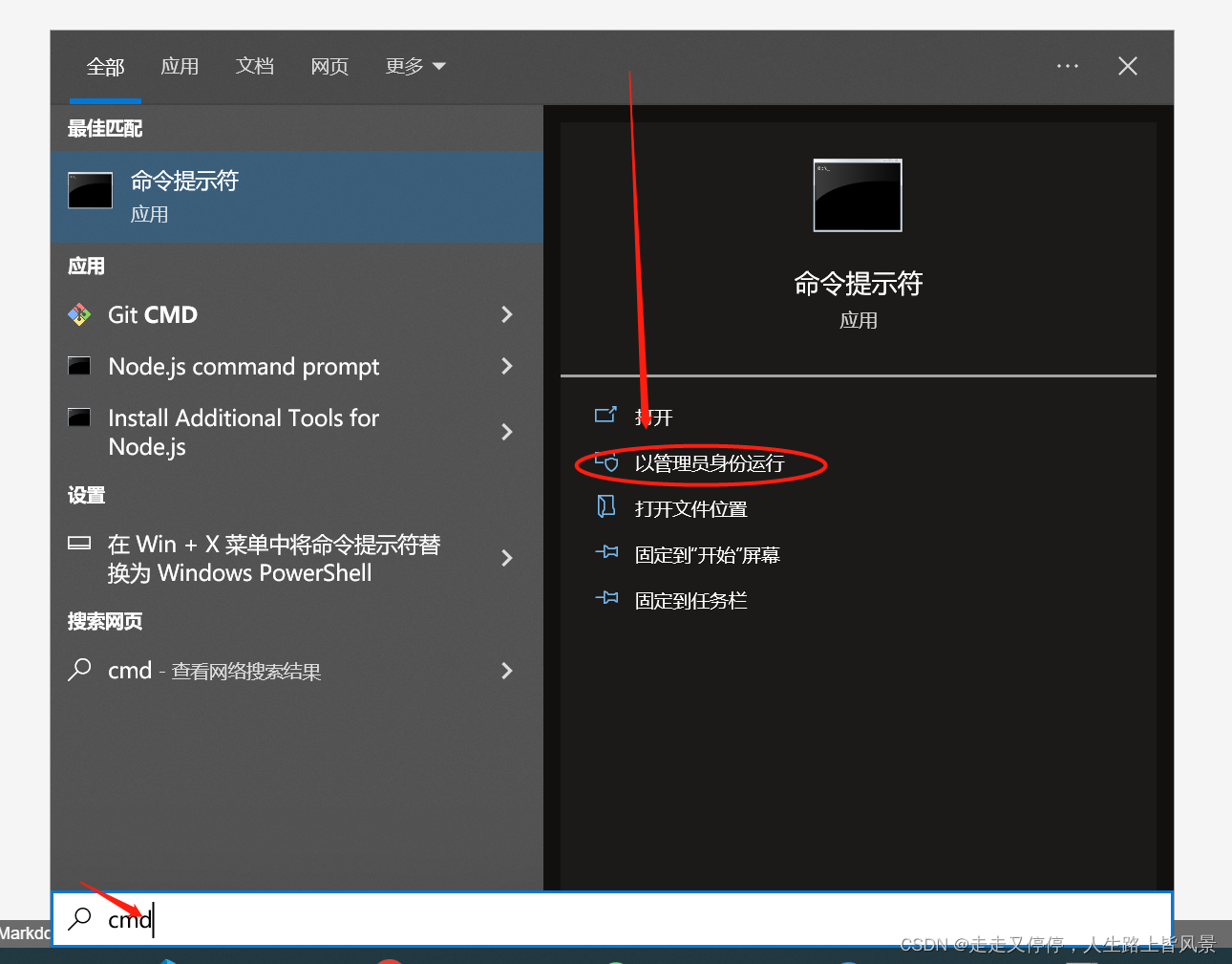
win10电脑无法联网,设置IPv4,点击属性无法打开,闪退
win10设置IPv4,点击属性无法打开,闪退 问题:win10设置IPv4,点击属性无法打开,闪退 问题:win10设置IPv4,点击属性无法打开,闪退 第1步:用管理员打开cmd命令窗口,然后输入下面的命令&…...

【数据结构】邻接表与邻接矩阵的转换
一.基本思想 1.邻接矩阵转换为邻接表: 先设置一个空的邻接表,然后查找邻接矩阵的值不为零元素,找到后在邻接表的单链表对应位置加入表边节点。 2.邻接表转换为邻接矩阵: 在邻接表上顺序取出每个表边结点,将邻接矩阵…...

VR智慧景区:VR赋能文旅产业,激活消费潜能
随着国家数字化战略的不断深入实施,文旅产业数字化转型的步伐也在逐渐加快,以VR技术赋能文旅产业,让文旅景区线上线下双渠道融合,进一步呈现文化底蕴、激活消费潜能。 VR智慧景区以沉浸式、互动式、科技感的方式,将景区…...

Spring Boot EasyPOI 使用指定模板导出Excel
相信大家都遇到过,用户提出要把界面上的数据导成一个Excel,还得是用户指定的Excel格式,用原生的POI,需要自己去实现,相信是比较麻烦的,所以我们可以使用开源的EasyPOI. 先上个图,看看是不是大家…...
postgresql:记录表膨胀引起的io问题的处理
文章目录 1. io异常2.查看profile报告2.1 生成事发时间段的pgprofile2.2 查看报告 3.检查table是否膨胀4.执行vacuum full5.总结 1. io异常 iostat -x 1 20 Device r/s w/s rkB/s wkB/s rrqm/s wrqm/s %rrqm %wrqm r_await w_await aqu-sz rareq…...
Windows下安装RabbitMQ
1.安装Erlang 因为RabbitMQ是用Erlang语言编写的,所以在安装RabbitMQ之前需要先安装Erlang。 如果还未安装Erlang,官方下载安装包,点击Download Windows installer下载Erlang Downloads - Erlang/OTP 下载Erlang/OTP后,双击otp的…...

广州华锐互动VRAR:利用VR开展刑事案件公安取证培训,沉浸式体验提升实战能力
随着科技的飞速发展,虚拟现实(VR)技术为我们的生活和工作带来了前所未有的便利。近年来,VR技术在刑事案件公安取证培训中的应用逐渐显现出其独特优势。通过模拟真实的犯罪现场,VR技术为学员提供了沉浸式的体验,使他们在安全的环境…...

消息消费过程
前言 本文介绍下Kafka消费过程, 内容涉及消费与消费组, 主题与分区, 位移提交,分区再平衡和消费者拦截器等内容。 消费者与消费组 Kafka将消费者组织为消费组, 消息只会被投递给消费组中的1个消费者。因此, 从不同消费组中的消费者来看, Kafka是多播(Pub/Sub)模式…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
