Vue3 动态设置 ref
介绍
在一些场景,ref设置是未知的需要根据动态数据来决定,如表格中的input框需要我们主动聚焦,就需要给每一个input设置一个ref,进而进行聚焦操作。
Demo
点击下面截图中的编辑按钮,自动聚焦到相应的输入框中。

<template><!-- 动态ref --><div class="test_ref"><div v-for="item in 9" :key="item"><span>{{ item }}</span><!-- 动态设置ref --><el-inputv-model="inputVal"placeholder="Please input":ref="(el:refItem) => handleSetInputMap(el, item)"/><el-button type="primary" :icon="Edit" @click="handleEdit(item)" /></div></div>
</template><script lang="ts" setup>
import { ref } from "vue";
import { Edit } from "@element-plus/icons-vue";
import { ComponentPublicInstance } from "vue";
type refItem = Element | ComponentPublicInstance | null;
const inputVal = ref();
const inputRefMap = ref({});/** 编辑 */
const handleEdit = (item: number) => {// 若输入框此时还没有渲染出来,如先隐藏再触发显示 需要使用nextTick进行聚焦inputRefMap.value[`Input_Ref_${item}`].input.focus();
};/** 动态设置Input Ref */
const handleSetInputMap = (el: refItem, item: number) => {if (el) {inputRefMap.value[`Input_Ref_${item}`] = el;}
};
</script><style lang="scss" scoped>
.test_ref {padding: 50px;> div {width: 300px;margin: 0 auto;display: flex;justify-content: center;align-items: center;gap: 20px;margin-bottom: 10px;}
}
</style>
效果

相关文章:

Vue3 动态设置 ref
介绍 在一些场景,ref设置是未知的需要根据动态数据来决定,如表格中的input框需要我们主动聚焦,就需要给每一个input设置一个ref,进而进行聚焦操作。 Demo 点击下面截图中的编辑按钮,自动聚焦到相应的输入框中。 &…...

fast lio 2 保存每一帧的点云PCD和里程计矩阵 Odom 在txt文件
修改了源代码的 laserMapping.cpp 文件,替换为下面的代码就可以保存了,注意里面有一个路径,需要修改为你的电脑的路径 // This is an advanced implementation of the algorithm described in the // following paper: // J. Zhang and S. Singh. LOAM: Lidar Odometry an…...

当前主流DDos方式有哪几类
随着互联网的普及和技术的进步,网络安全问题日益凸显。DDoS攻击作为其中一种常见且具破坏性的攻击方式,受到了广泛关注。小德将带领大家一起来了解当前流行的三种DDoS攻击方式。 1. 容量耗尽攻击 容量耗尽攻击是最常见也是最直接的DDoS攻击方式。攻击者通…...
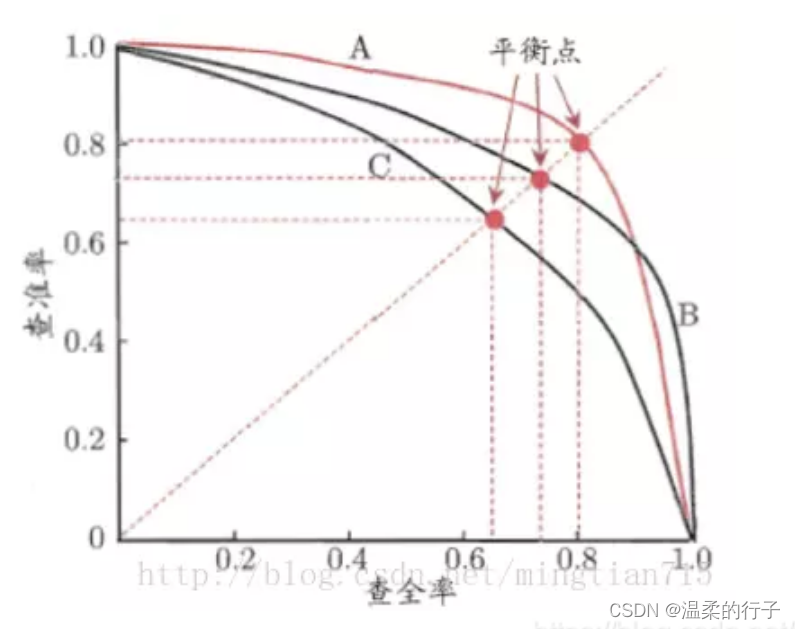
神经网络常见评价指标AUROC(AUC-ROC)、AUPR(AUC-PR)
神经网络的性能可以通过多个评价指标进行衡量,具体选择哪些指标取决于任务的性质。以下是神经网络中常见的评价指标: 准确性(Accuracy): 准确性是最常见的分类任务评价指标,表示模型正确预测的样本数占总样…...

Apache Doris安装部署
Apache Doris安装部署 版本: CentOS 7.6 Apache Doris 0.14.0 编译 选择合适的版本进行下载,此次选择0.14.0版本 下载 | Apache Doris 一、CentOS编译 1 安装依赖 sudo yum groupinstall Development Tools && sudo yum install maven c…...

Excel查询时用vlookup或者xlookup时,虽然用的参数选择的是精确匹配,但是发现不能区分大小写,应该如何解决?
Excel查询时用vlookup或者xlookup时,虽然用的参数选择的是精确匹配,但是发现不能区分大小写,应该如何解决? Index函数解决 INDEX([excel1.xlsx]Sheet1!$E:$E,MATCH(1,EXACT(G5,[excel1.xlsx]Sheet1!$E:$E)*1,0))重点说明&#x…...
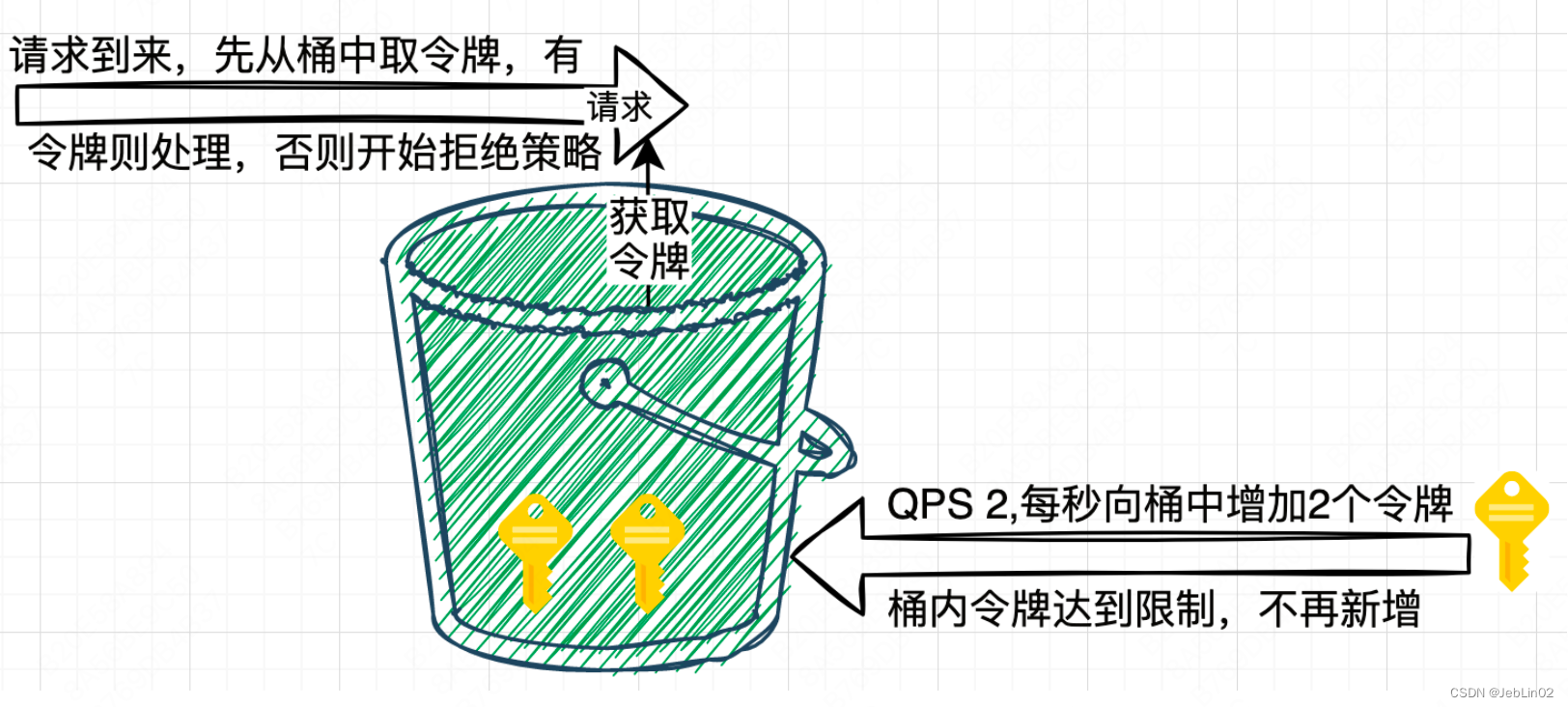
4种经典的限流算法
0、基础知识 1000毫秒内,允许2个请求,其他请求全部拒绝。 不拒绝就可能往db打请求,把db干爆~ interval 1000 rate 2; 一、固定窗口限流 固定窗口限流算法(Fixed Window Rate Limiting Algorithm)是…...
<MySQL> 什么是数据库事务?事务该如何使用?
目录 一、事务的概念 二、事务的核心特性 三、事务操作中的常见BUG 3.1 脏读 3.2 不可重复读 3.3 幻读 四、隔离级别 五、使用事务 一、事务的概念 “事务”是指一组操作,在逻辑上是不可分割的,组成这组操作的各个语句,或者全部执行成…...
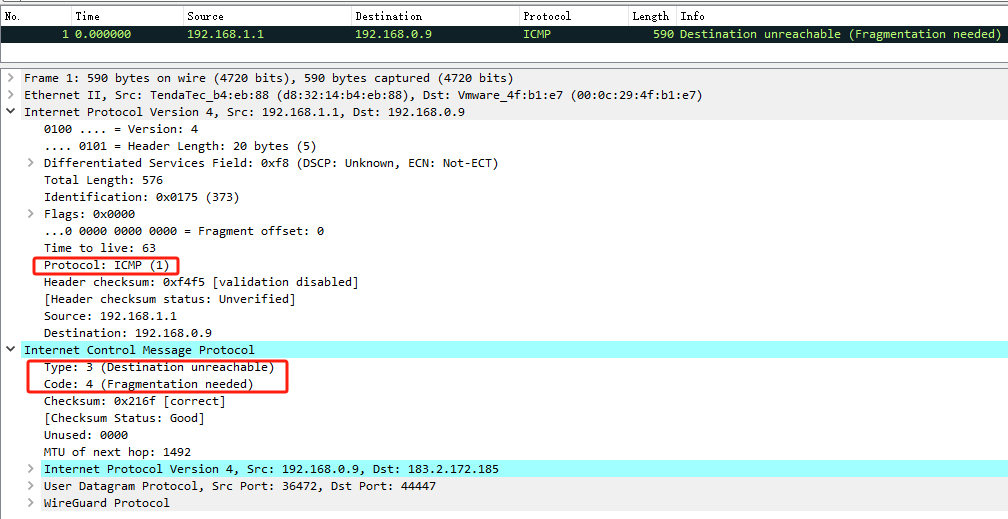
Linux 网络:PMTUD 简介
文章目录 1. 前言2. Path MTU Discovery(PMTUD) 协议2.1 PMTUD 发现最小 MTU 的过程 3. Linux 的 PMTUD 简析3.1 创建 socket 时初始化 PMTUD 模式3.2 数据发送时 PMTUD 相关处理3.2.1 源头主机发送过程中 PMTU 处理3.2.2 转发过程中 PMTUD 处理 4. PMTUD 观察5. 参考链接 1. 前…...

BatchNormalization:解决神经网络中的内部协变量偏移问题
ICML2015 截至目前51172引 论文链接 代码连接(planing) 文章提出的问题 减少神经网络隐藏层中的”内部协变量偏移”问题。 在机器学习领域存在“协变量偏移”问题,问题的前提是我们划分数据集的时候,训练集和测试集往往假设是独立同分布(i.i.d)的,这种独立同分布更有利于…...

DAC实验(DAC 输出三角波实验)(DAC 输出正弦波实验)
DAC 输出三角波实验 本实验我们来学习使用如何让 DAC 输出三角波,DAC 初始化部分还是用 DAC 输出实验 的,所以做本实验的前提是先学习 DAC 输出实验。 使用 DAC 输出三角波,通过 KEY0/KEY1 两个按键,控制 DAC1 的通道 1 输出两种…...
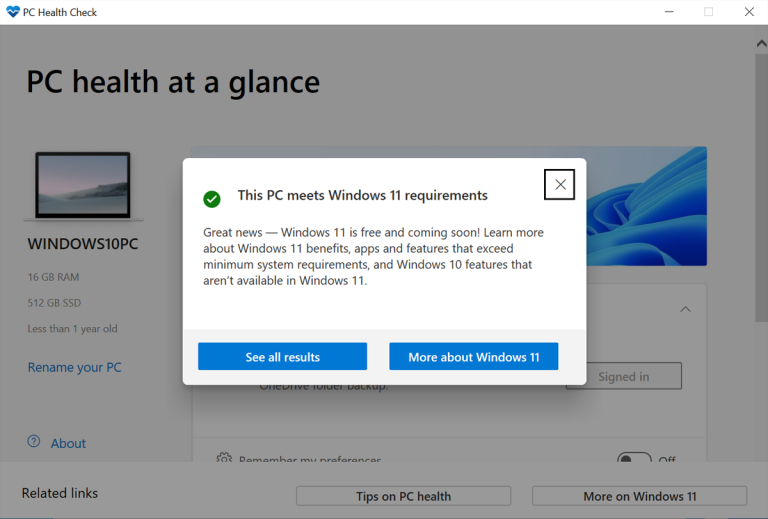
许多网友可能还不知道,升级到Windows 11其实没那么复杂,只要符合几个条件可以了
如果你的Windows 10电脑可以升级Windows 11,现在怎么办?有几种方法可以免费安装新的操作系统。以下是你的选择。 如果你想升级到Windows 11,你可以随时购买一台已经安装了操作系统的新电脑。然而,如果你目前的Windows 10 PC满足所有必要的升级要求,那么在Windows 11免费的…...
ubuntu下载conda
系统:Ubuntu18.04 (1)下载安装包 wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/Anaconda3-2021.11-Linux-x86_64.sh 报错错误 403:Forbidden 解决方法 wget -U NoSuchBrowser/1.0 https://mirrors.tuna.tsingh…...

重磅 | 进一步夯实生态建设,朗思科技与阿里龙蜥完成兼容性认证
近日,北京朗思智能科技有限公司(以下简称“朗思科技”)自主研发的数字员工产品与OpenAnolis龙蜥社区龙蜥操作系统(Anolis OS)8完成兼容性认证。测试结果显示,双方产品相互兼容,功能正常…...

Qt给控件添加图片
双击qrc文件,选择下面的addFiles,将图片添加进来,然后选中图片右键Select All 设置控件字符: ui.btnSet->setText(""); 设置资源: ui.btnSet->setStyleSheet("QPushButton{background-image:…...

3.6-Dockerfile语法梳理及最佳实践
WORKDIR是设置当前docker的工作目录 ADD 和 COPY 为了将本地的一些文件添加到docker image里面,ADD 和 COPY的作用特别像,但是ADD 和 COPY还有一些区别,ADD不仅可以添加本地文件到docker里面,还可以将文件在添加到docker image里面…...
springboot集成nacos并实现自动刷新
目录 1.说明 2.示例 3.自动刷新的注意点 1.说明 springboot项目中存在好多配置文件,比如配置数据信息,redis信息等等,配置文件可以直接放在代码,也可以放在像nacos这样的组件中,实现动态的管理,修改配置…...

java面试八股文2023完整版详解110题附带答案
以下是一份Java面试八股文2023,涵盖了Java编程语言的核心概念和常用技术,帮助你更好地准备面试。 1. Java语言有哪些特点? Java语言是一种面向对象的编程语言,具有简单、面向对象、分布式、多线程、动态等优点。它是一种跨平台的…...

微服务实战系列之Token
前言 什么是“Token”? 它是服务端生成的一串字符串,以作客户端进行请求的一个令牌,当第一次登录后,服务器生成一个Token便返回给客户端;以后客户端只携带此Token请求数据即可。 简言之,Token其实就是用户身…...

DRF纯净版项目搭建和配置
一、安装模块和项目 1.安装模块 pip install django pip install djangorestframework pip install django-redis # 按需安装 2.开启项目和api (venv) PS D:\pythonProject\env_api> django-admin startproject drf . (venv) PS D:\pythonProject\env_api> python ma…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
