图神经网络:消息传递算法

一、说明
二、图网络简述
图神经网络是一种用于以图形式呈现的数据的神经网络。图形是由顶点(节点)和边组成的空间结构。有许多结构表示为图形:三维空间(x,y,z)中的结构,如物质分子(例如咖啡因)、蛋白质(由氨基酸组成)、DNA、计算机网络以及社交网络等结构。以下是一些使用 Wolfram Mathematica 制作的例子:
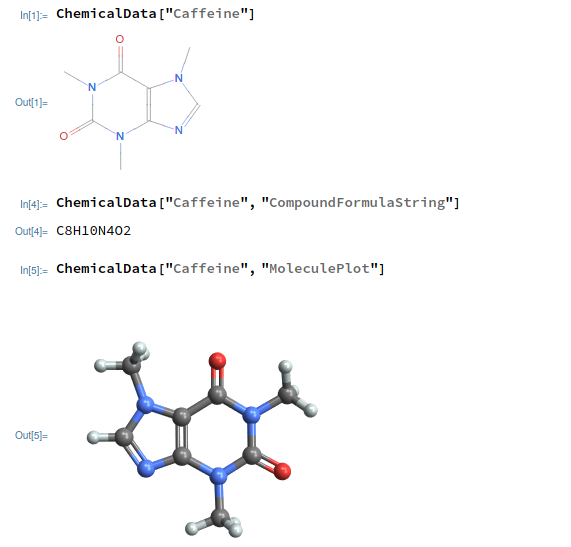
咖啡因的分子结构

蛋白
蛋白质中原子的 XYZ 坐标

社交网络
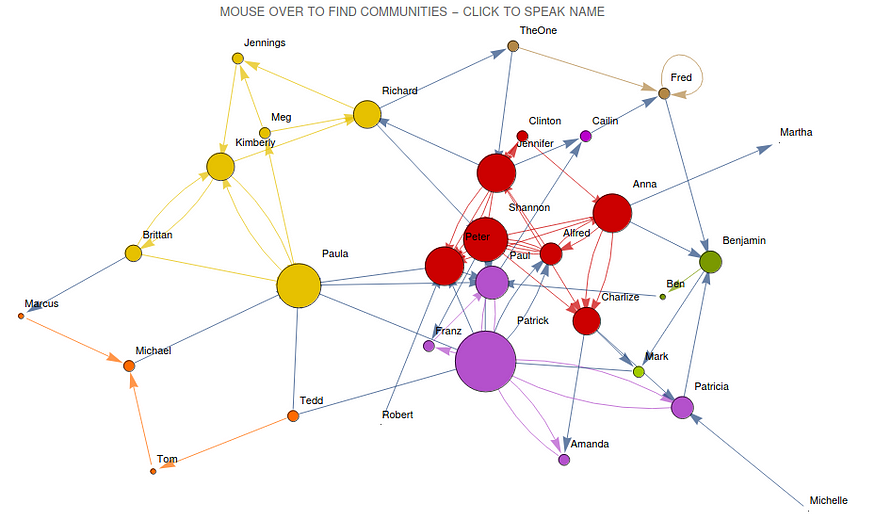
社交网络社区
基本上,每个节点代表一个人、一个原子、一个金融交易,这些节点通过边连接,在这些实体之间建立关系。在人与人之间,这可能是领带的强度、社交距离、亲密程度。在分子结构中的原子中,这些边缘可能是共价键。在金融交易中,这些边缘可以定义某人与欺诈交易的距离。
考虑到社交网络的例子(如上图),我们有密集连接的人集群,可能与“影响者”有关,也有薄弱环节(弱纽带),它们连接不同的人群,允许信息的多样性。当我们亲自或通过社交媒体相互交谈时,我们的信息会通过这个社交网络传播,并且可能会受到其内容的变形和误解的影响。原子及其电磁特性也会发生同样的情况:其他原子离得越近,它们受这些电磁特性的影响就越大。因此,经过一段距离后,这种影响会逐渐消失。此外,如果允许这种影响渗透到所有网络结构中,则由于饱和,整个网络可能会收敛到单一状态。
三、图网络的向量模型
但是,我们如何才能用数学方式来表示这些复杂的关系,以便能够对这些相互作用进行建模呢?首先,我们应该定义每个参与者之间的联系。这是通过邻接矩阵完成的,其中相同的个体被放置在该矩阵的行和列中:

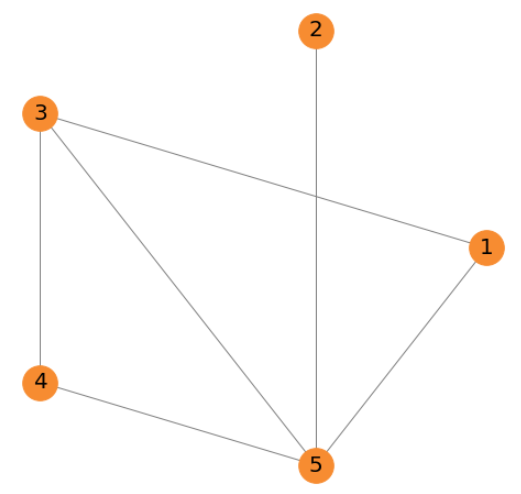
基于邻接矩阵的网络结构
此邻接矩阵中的每个数字 1 都表示一个连接。我们有一个 5 x 5 矩阵,其中节点 1 到 5 分别放置在线和列中。所以,如果你拿个体 2,他只与个体 5 相连。个体 1 连接到个体 3 和 5,依此类推。为了绘制这个网络,我使用了以下代码:
import numpy as np
import networkx as nxAdj = np.array([[0, 0, 1, 0, 1],[0, 0, 0, 0, 1], [0, 0, 0, 1, 1], [0, 0, 1, 0, 1], [1, 1, 0, 0, 0]]
)
g = nx.from_numpy_array(Adj)
pos = nx.circular_layout(g)fig, ax = plt.subplots(figsize=(8,8))
nx.draw(g, pos, with_labels=True, labels={i: i+1 for i in range(g.number_of_nodes())}, node_color='#f78c31', ax=ax, edge_color='gray', node_size=1000, font_size=20, font_family='DejaVu Sans')现在我们将邻接矩阵乘以由行数组成的向量。因此,我们将得到一个 5 x 5 矩阵乘以 5 x 1 向量。这意味着 n x p 乘以 p x m 将得到一个 n x m 向量。在本例中,5 x 1 向量:
H = Adj @ np.array([1,2,3,4,5]).reshape(-1,1)请注意,为了进行此乘法,您需要将 p x m 向量转置为 [1,2,3,4,5],并逐个元素乘以邻接矩阵和总和的那行的每个元素。结果是相连邻域的总和。按住 H 一会儿。
现在我们将找到对角线度矩阵,它由对角线中的邻域大小组成,即矩阵中每一列的总和:
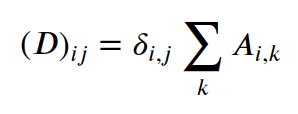
D = np.zeros(Adj.shape)
np.fill_diagonal(D, Adj.sum(axis=0))
对角线度矩阵
现在,我们将为每个边分配一个权重。我们通过将恒等矩阵除以对角度矩阵来做到这一点。
D_inv = np.linalg.inv(D)
倒置度矩阵
通过将倒置的 D 乘以邻接矩阵,我们将得到一个平均的邻接矩阵:

平均邻接矩阵
当我们处理一个没有单个值的节点,而是特征向量的集合时,平均的概念非常重要,就像图卷积网络一样。
但是,我们真正想要操作的是消息传递算法,如下所示:
![]()
反复应用的帽子将允许信息在图网络中流动。假设波浪号等于邻接矩阵加单位矩阵,我们有:
![]()
g = nx.from_numpy_array(Adj)
Adj_tilde = Adj + np.eye(g.number_of_nodes())
现在我们需要创建 D 波浪号的平方根。我们创建一个零矩阵,并将邻接矩阵波浪号的线和值相加。
D_tilde = np.zeros_like(A_tilde)
np.fill_diagonal(D_tilde, A_tilde.sum(axis=1).flatten())
然后我们计算 D 波浪号的平方反比根:
D_tilde_invroot = np.linalg.inv(sqrtm(D_tilde))现在我们已经有了 A 波浪号,以及 D 波浪号的平方反比根,我们可以计算出 A 帽子:
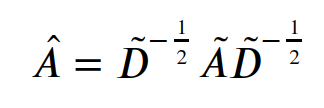
A-hat(帽子)的程序表示:
A_hat = D_tilde_invroot @ A_tilde @ D_tilde_invroot请注意,numpy 中的 @ 与 matmul 的意思相同。

A-hat 帽子的结果
现在我们将实现消息传递算法。让我们从我们拥有的消息向量 (H) 开始,检查它在图网络中的流动方式。我们知道:
H = Adj @ np.array([1,2,3,4,5]).reshape(-1,1)现在我们让信息流在图网络中:
epochs = 9
information = [H.flatten()]
for i in range(epochs):H = A_hat @ Hinformation.append(H.flatten())四、图神经网的可视化
让我们看看这个热图中的信息流。注意每个个体(x 轴)如何随时间(y 轴)获取或丢失信息。
import matplotlib.pyplot as pltplt.imshow(information, cmap='Reds', interpolation='nearest')
plt.show()
让我们把它画出来:
fig, ax = plt.subplots(figsize=(12, 12))
from time import timefor i in range(0,len(information)):colors = information[i]nx.draw(g, pos, with_labels=True, labels=node_labels, node_color=colors*2, ax=ax, edge_color='gray', node_size=1500, font_size=30, font_family='serif',vmin= np.array(information).min(), vmax=np.array(information).max())plt.title("Epoch={}".format(i))plt.savefig('/home/user/Downloads/message/foo{}.png'.format(time()), bbox_inches='tight', transparent=True)import glob
from PIL import Imagefp_in = "/home/user/Downloads/message/foo*.png"
fp_out = "/home/user/Downloads/message100_try.gif"img, *imgs = [Image.open(f) for f in sorted(glob.glob(fp_in))]
img.save(fp=fp_out, format='GIF', append_images=imgs,save_all=True, duration=1200, loop=0)从视觉上看,图网络中的信息流在每个时期都如下所示:

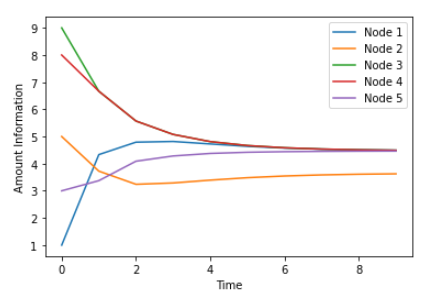
在下图中,我们可以看到网络的每个节点随时间推移有多少信息。请注意节点 1、3、4 和 5 的收敛:
有关消息传递算法在基于代理的模型中的实际应用,请参阅我在 COMSES 上使用 Python 和 NetLogo 制作的模型:鲁本斯·津布雷斯
相关文章:

图神经网络:消息传递算法
一、说明 图网络-GNN(Graph Neural Networks)是近几年研究的主题之一,虽不及深度神经网络那么火爆,但在一些领域,如分子化学方面是不得不依赖的理论。本文就一些典型意义的图神经网络消息传递展开阐述。 二、图网络简述…...

安全+Linux!IBM新一代大型机Z14全新发布
导读本周,以“架构 人机同行”为主题的IBM Systems创行者高峰论坛在北京召开,IBM全球及大中华区硬件系统部负责人,金融、医疗、制造等领域的企业、合作伙伴共与这一年度盛会,探讨认知时代下的基础架构技术趋势及IBM硬件系统业务的…...

Java中的局部变量和成员变量的区别
局部变量和成员变量的区别 区别1:代码中位置不同 成员变量:类中方法外定义的变量 局部变量:方法中定义的变量 代码块中定义的变量 区别2:代码的作用范围 成员变量:当前类的很多方法 局部变量:当前一…...
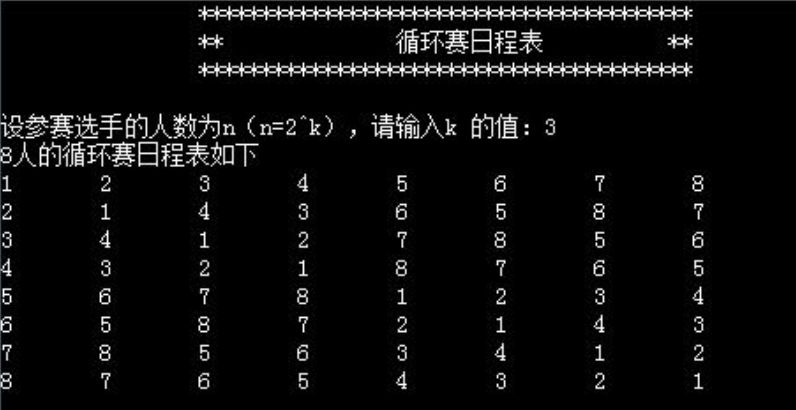
基于C++实现循环赛日程表(分治算法)
一、问题描叙 设有n2^k个运动员,要进行网球循环赛。现在要设计一个满足以下要求的比赛日程表 每个选手必须与其他n-1个选手各赛一场每个选手一天只能赛一次循环赛一共进行n-1天 二、问题分析 按此要求可将比赛日程表设计成n行n-1列的表,在表中第 i 行…...

基于uni-app的汽车租赁app的设计与实现
1.项目背景及意义 项目背景: 随着人们生活水平的提高,汽车租赁服务在城市中变得越来越普及。传统的租车方式存在一些问题,比如租车流程繁琐、费用不透明、选择有限等。因此,开发一款基于uni-app的汽车租赁app成为了满足用户需求…...
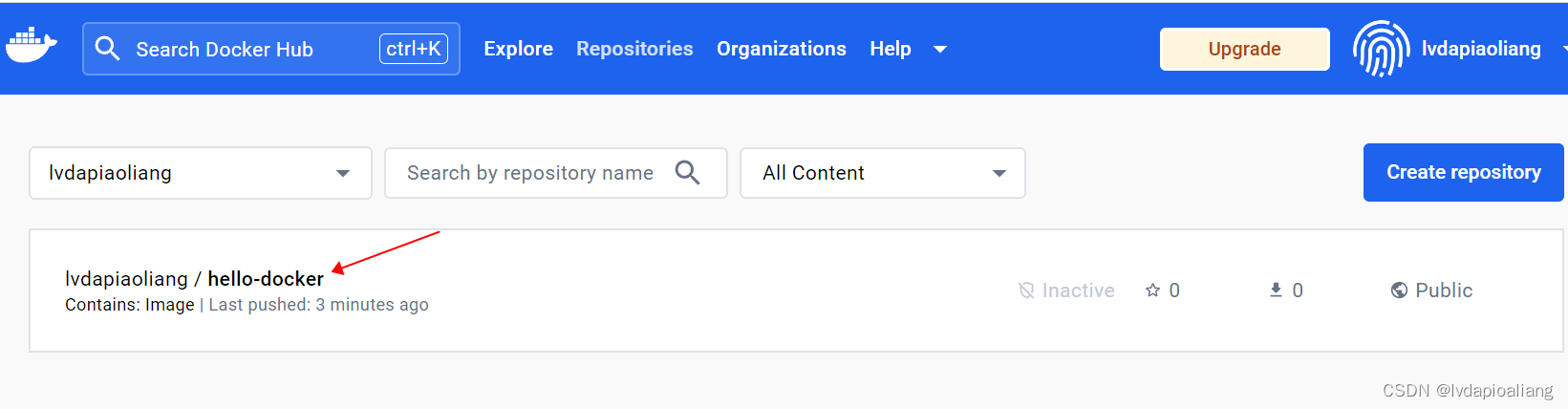
3.8-镜像的发布
如果我们想将image push到docker hub里面,那么我们的image的名字一定要是这种格式:docker hub id/imageName,例如:lvdapiaoliang/hello-docker docker hub个人账户设置地址: 在push之前要先登录: docker l…...
Navicat 基于 GaussDB 主备版的快速入门
Navicat Premium(16.2.8 Windows版或以上) 已支持对GaussDB 主备版的管理和开发功能。它不仅具备轻松、便捷的可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结构同步、协同合作、数据迁移等),这…...

String的字符串拼接
java中 String a “123” “234”; String b “123”; String c b “234”; 其中a和c的区别是什么? a c 为什么为false 在Java中,字符串的处理特别是涉及到字符串常量和字符串变量的连接时,会涉及到字符串池(String Pool&a…...
反渗透水处理成套设备有哪些
反渗透水处理成套设备主要包括反渗透装置、预处理系统、控制系统等部分。 反渗透装置:反渗透水处理设备的核心部分,由反渗透膜、压力容器、膜组件等组成。反渗透膜是一种高分子材料制成的半透膜,能够截留水中的溶解盐、有机物、细菌等杂质&a…...

DPC15 国产带有 SPI 接口的独立 CAN 控制器兼容替代MCP2551
DPC15是一款独立控制器局域网络(Controller Area Network,CAN)协议控制器,完全支持CAN V2.0B技术规范。该器件能发送和接收标准和扩展数据帧以及远程帧。 DPC15自带的两个验收屏蔽寄存器和六个验收滤波寄存器可以过滤掉不想要的报…...

【ELK01】ELK简介以及ElasticSearch安装、ES客户端工具-Head安装、报错问题整理
有一段时间没有更新这个专栏了,最近在用ELK相关的技术,今天开始写一下ELK的系列的内容,与大家共同学习 一、什么是ELK ELK 是elastic公司提供的一套完整的日志收集以及展示的解决方案,是三个产品的首字母缩写,分别是ElasticSearch、Logstash 和 Kibana。 1. E-ELASTICS…...

根据音频绘制频谱
根据音频链接绘制频谱图 封装 // 可以这样使用 也可以 import { AudioContext } from standardized-audio-context; const getAudioContext window.AudioContext ||window.webkitAudioContext ||window.mozAudioContext ||window.msAudioContext;const clearArr []export c…...
SSL证书对网站SEO的好处
随着网络安全意识的提高,越来越多的网站开始采用SSL证书来保护自己的数据传输过程。那么,SSL证书真的能为网站SEO带来好处吗?下面将为您分析这个问题。 加强用户体验和信任度 SSL证书不仅能确保数据传输的安全性,还能让客户感受…...

YB506AB是一款理电池充、放电管理专用芯片,集成锂电池充电管理和降压DC-DC电路。
YB506AB 锂电转可充电AA/AAA电池专用SOC芯片 概述: YB506AB是一款理电池充、放电管理专用芯片,集成锂电池充电管理和降压DC-DC电路。充电过程满足锂电池三段式滑流/恒流/恒压充电规范,B506内部的线性充电电路采用了恒流可配置模式,可以通过…...
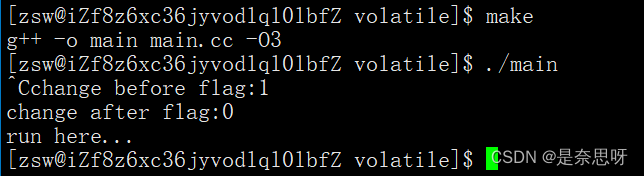
Linux | C语言中volatile关键字的理解
目录 前言 一、代码引入 二、现象解释 三、具体引用 前言 本章主要讲解介绍volatile关键的作用与使用场合;深刻理解volatile关键字;本文你需要有信号相关的基础知识; Linux | 信号-CSDN博客 一、代码引入 首先,我们来查看下面…...

汇编层面有三个主要的操作对象
1.为啥会有addi指令? 在汇编层面有三个主要的操作对象:寄存器,内存,立即数,它们是完全不同,不可以混淆,组织结构也不一样的不同对象,所以不能单纯拿针对寄存器的指令去处理内存和立…...

React中的Redux:简介和实例代码
React是一个流行的JavaScript库,用于构建用户界面。它提供了一种简单而强大的方式来构建交互式的界面。Redux是一个用于管理应用程序状态的JavaScript库。它可以与React一起使用,以帮助管理React应用程序的状态。 引言 在本文中,我们将介绍R…...

Modbus转Profinet网关在金银精炼控制系统中应用案例
金银精炼控制系统中采用Modbus转Profinet网关(XD-MDPN100)连接1200plc与PID控制阀门进行通讯,通过控制PID阀门的大小来实现温度的恒温控制。这一系统的好处在于它能够提高金银精炼过程的效率和精确度。PID控制阀门可以根据温度的变化实时调整…...

小程序商城免费搭建之java商城 电子商务Spring Cloud+Spring Boot+二次开发+mybatis+MQ+VR全景+b2b2c
1. 涉及平台 平台管理、商家端(PC端、手机端)、买家平台(H5/公众号、小程序、APP端(IOS/Android)、微服务平台(业务服务) 2. 核心架构 Spring Cloud、Spring Boot、Mybatis、Redis 3. 前端框架…...
)
Rabin加解密算法(python3)
Rabin加解密算法 详细代码如下: # 空空 # dahouzi.cn import random from sympy import isprimedef decrypt_rabin(c, p, q):"""解密 Rabin 密文Args:c (int): 密文p (int): 素数 pq (int): 素数 qReturns:tuple: 解密结果 M1, M2, M3, M4"&q…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
