golang archive/tar库的学习
archive/tar 是 Golang 标准库中用于读取和写入 tar 归档文件的包。tar 是一种常见的文件压缩格式,它可以将多个文件和目录打包成单个文件,可以用于文件备份、传输等场景。
以下是一些学习 archive/tar 包的建议:
-
了解 tar 文件格式。在学习 archive/tar 之前,建议先了解 tar 文件的格式,例如 tar 文件头部的结构,以及如何读取和写入 tar 文件。
-
学习官方文档。官方文档是学习 archive/tar 最好的资源之一。您可以在 Golang 官方网站的文档中找到完整的 archive/tar 包文档,其中包括各种结构体,函数,接口以及使用示例。
-
学习 tar 归档文件的读取和写入。archive/tar 提供了
tar.Reader和tar.Writer结构体,分别用于读取和写入 tar 归档文件。您可以使用这两个结构体来读取和写入 tar 归档文件,并操作其中的文件和目录。 -
学习 tar 归档文件的压缩和解压缩。archive/tar 可以与 compress 包结合使用,用于压缩和解压缩 tar 归档文件。您可以使用
gzip.Writer和gzip.Reader结构体来压缩和解压缩 tar 归档文件。 -
学习 tar 归档文件的权限和时间戳。tar 归档文件中包含每个文件的权限和时间戳等元数据信息。archive/tar 提供了相应的字段和方法来读取和写入这些元数据信息。
-
学习 tar 归档文件的扩展功能。tar 归档文件可以支持一些扩展功能,例如增量备份、增量更新等。archive/tar 中提供了一些相应的方法和接口,可以帮助您实现这些功能。
希望这些建议可以帮助您更好地学习和掌握 archive/tar 包。
相关文章:

golang archive/tar库的学习
archive/tar 是 Golang 标准库中用于读取和写入 tar 归档文件的包。tar 是一种常见的文件压缩格式,它可以将多个文件和目录打包成单个文件,可以用于文件备份、传输等场景。 以下是一些学习 archive/tar 包的建议: 了解 tar 文件格式。在学习…...
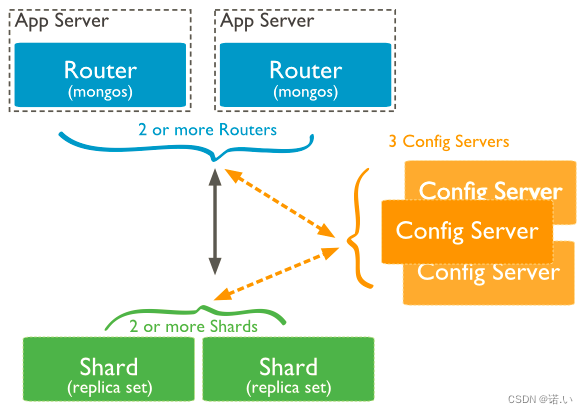
MongoDB 详细教程,这一篇就够啦
文章目录1. 简介2. 特点3. 应用场景4. 安装(docker)5. 核心概念5.1 库5.2 集合5.3 文档6. 基本操作6.1 库6.1.1 增6.1.2 删6.1.3 改6.1.4 查6.2 集合6.2.1 增6.2.2 删6.2.3 改6.2.4 查6.3. 文档6.3.1 增6.3.2 删6.3.3 改6.3.4 查1. 语法2. 对比语法3. AN…...

python为什么慢
解释性 python是动态类型解释性语言,不管使用哪种解释器 因为“解释性语言”这个概念更多地是指代码的执行方式,而不是编译方式。在解释性语言中,代码在执行时会一行一行地解释并执行,而不是预先编译为机器语言。而即使使用了PyP…...

Android kotlin 组件间通讯 - LiveEventBus 及测试(更新中)
<<返回总目录 文章目录 一、LiveEventBus是什么二、测试一、LiveEventBus是什么 LiveEventBus是Android中组件间传递消息,支持AndroidX,Event:事件,Bus:总线 范围全覆盖的消息总线解决方案 进程内消息发送App内,跨进程消息发送App之间的消息发送更多特性支持 免配…...

linux服务器时间同步
Linux服务器时间同步 需求:两台以上服务器之间的时间同步,以其中一台服务器为时间源,其余服务器同步这台时间源服务器的时间 其中,时间源服务器需要有访问外网权限,不然时间源服务器无法同互联网同步最新的时间&#…...
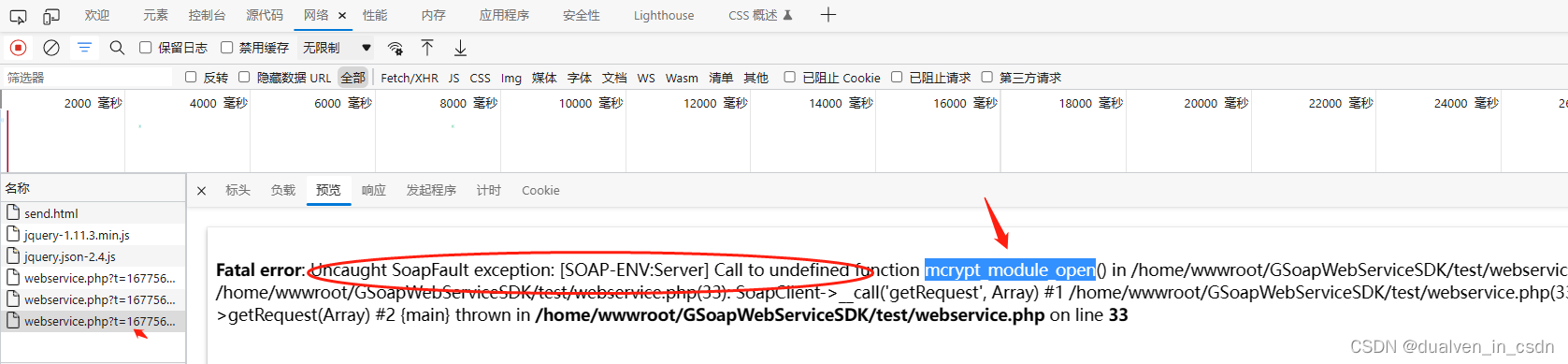
扒系统CR8记录
目录 终极改造目标 过程记录 参考 为了将一套在线安装的系统,在不了解其架构、各模块细节的基础上,进行扒弄清楚,作以下记录。 终极改造目标 最终的目标,就是只通过CreMedia8_20230207.tar.gz解压 install 就把业务包安装了&…...
面试题(基础篇)
1、你是怎样理解OOP面向对象的面向对象是利于语言对现实事物进行抽象。面向对象具有以下特征:(1)继承:继承是从已有类得到继承信息创建新类的过程(2)封装:通常认为封装是把数据和操作数据的方法…...

如何利用ReconPal将自然语言处理技术应用于信息安全
关于ReconPal 网络侦查一直是网络安全研究以及渗透测试活动中最重要的阶段之一,而这一阶段看起来很容易,但往往需要很大的努力和很强的技术才能做好来。首先,我们需要使用正确的工具、正确的查询/语法以及正确的操作,并将所有信息…...

攻略 | 6步帮助中小微企业开拓东盟机电产品市场
如何帮助中小微外贸企业在东盟市场拓展机电产品一般贸易?随着全球化的发展,越来越多的中小微外贸企业开始涉足国际贸易。对于机电产品行业而言,东盟市场是一个非常重要的出口目的地。本文将为您介绍如何帮助中小微外贸企业在东盟市场拓展机电…...
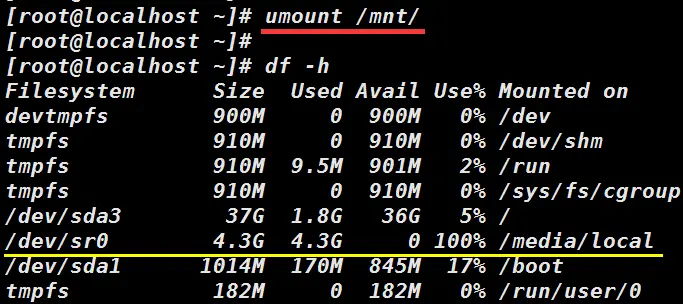
Linux服务器磁盘分区、挂载、卸载及报错处理
整体操作是:先对磁盘进行格式化,格式化后挂载到需要的挂载点,最后添加分区启动表,以便下次系统启动时自动挂载。一、linux分区1、Linux来说wulun有几个分区,分给哪一目录使用,他归根结底只有一个根目录&…...
JavaScript基础语法入门
一. JS简介 JavaScript , 简称JS, JS最初只是为了进行前端页面开发, 但随这后来JS越来越火之后, JS就被赋予了更多的功能, 可以用来开发桌面程序, 手机App, 服务器端的程序等… JS是一种动态类型, 弱类型的脚本语言, 通过解释器运行, 主要在客户端和浏览器上运行, 比如Chrome…...

Linux基础命令-ln创建链接文件
文章目录 ln 命令介绍 命令格式 基本参数 参考实例 1) 创建文件的硬链接 2)创建文件的软链接 3)创建链接文件时,相同目标文件创建备份文件 命令总结 ln 命令介绍 先看下帮助文档中的含义 NAME ln - make links …...
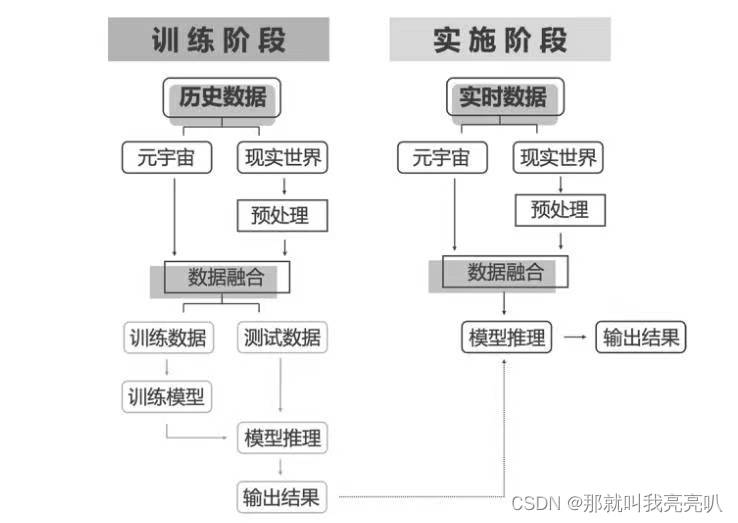
Day21【元宇宙的实践构想07】—— 元宇宙与人工智能
💃🏼 本人简介:男 👶🏼 年龄:18 🤞 作者:那就叫我亮亮叭 📕 专栏:元宇宙 0.0 写在前面 “元宇宙”在2021年成为时髦的概念。元宇宙到底是什么?元宇…...
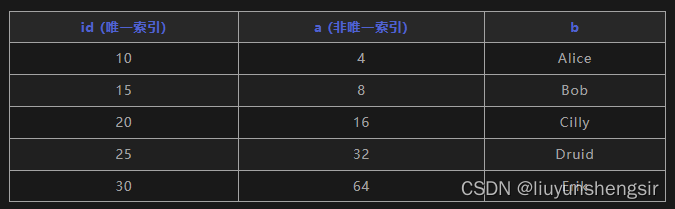
MySQL的InnoDB 三种行锁,SQL 语句加了哪些锁?
InnoDB 三种行锁: Record Lock(记录锁):锁住某一行记录 Gap Lock(间隙锁):锁住一段左开右开的区间 Next-key Lock(临键锁):锁住一段左开右闭的区间 哪些语句…...
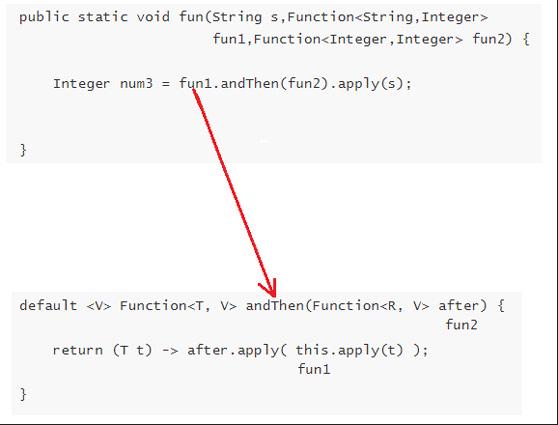
Java培训:深入解读函数式接口
函数式编程是一种编程规范或一种编程思想,简单可以理解问将运算或实现过程看做是函数的计算。 Java8为了实现函数式编程,提出了3个重要的概念:Lambda表达式、方法引用、函数式接口。现在很多公司都在使用lambda表达式进行代码编写,…...

scratch潜水 电子学会图形化编程scratch等级考试一级真题和答案解析2022年12月
目录 scratch潜水 一、题目要求 1、准备工作 2、功能实现 二、案例分析...
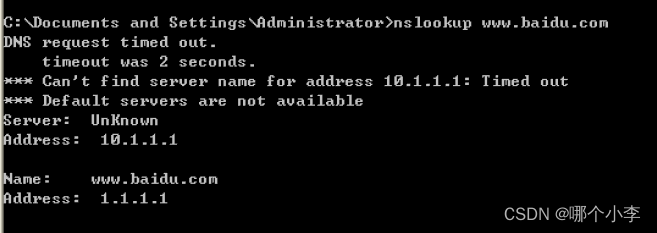
DNS服务器部署的详细操作(图文版)
DNS服务器的部署 打开虚拟机后查看已经开放的端口,可以看到没有TCP53、UDP53,说明DNS服务端口没有打开 打开我的电脑—双击CD驱动器— 选择安装可选的Windows组件 选择网络服务—域名系统(DNS)— 点击下一步后会弹出如下弹…...

Compose – List / Detail: Basics实现
Compose – List / Detail: Basics实现 在androidx中有SlidingPanelLayout可以实现折叠屏的列表详情功能,但在Compose 中还没有官方的实现,那么下面我们用Compose做一些实现。 List / Detail 我们追求的基本行为是当 UI 具有项列表时。当用户点击列表…...

【Java】TCP网络编程(字节/符流)
文章目录概念TCP网络编程ServerSocketsocket使用区别和原理演示概念 TCP(传输控制协议)是一种面向连接的协议,用于在计算机网络中可靠地传输数据。TCP是Internet协议族中的一个核心协议,它在传输层提供可靠、有序、基于流的传输服…...

Linux之init.d、rc.d文件夹说明
备注:Ubuntu没有rc.d文件夹,原因看问题四 Linux的几个重要文件 rc.d,init.d文件夹的说明 今天在研究mysql的安装的时候,最后一步要创建一个软连接,使得mysql服务可以自启动,代码如下: ln -s…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
