LeetCode 1145. 二叉树着色游戏 -- 简单搜索
- 二叉树着色游戏
提示
中等
199
相关企业
有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。
最开始时:
「一号」玩家从 [1, n] 中取一个值 x(1 <= x <= n);
「二号」玩家也从 [1, n] 中取一个值 y(1 <= y <= n)且 y != x。
「一号」玩家给值为 x 的节点染上红色,而「二号」玩家给值为 y 的节点染上蓝色。
之后两位玩家轮流进行操作,「一号」玩家先手。每一回合,玩家选择一个被他染过色的节点,将所选节点一个 未着色 的邻节点(即左右子节点、或父节点)进行染色(「一号」玩家染红色,「二号」玩家染蓝色)。
如果(且仅在此种情况下)当前玩家无法找到这样的节点来染色时,其回合就会被跳过。
若两个玩家都没有可以染色的节点时,游戏结束。着色节点最多的那位玩家获得胜利 ✌️。
现在,假设你是「二号」玩家,根据所给出的输入,假如存在一个 y 值可以确保你赢得这场游戏,则返回 true ;若无法获胜,就请返回 false 。
示例 1 :
输入:root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3
输出:true
解释:第二个玩家可以选择值为 2 的节点。
示例 2 :
输入:root = [1,2,3], n = 3, x = 1
输出:false
提示:
树中节点数目为 n
1 <= x <= n <= 100
n 是奇数
1 <= Node.val <= n
树中所有值 互不相同
题解
一开始就想复杂了,以为是博弈论和动态规划,然后静心下来想了下,发现不是。。。。。
这个题目很简单,因为是树结构(如果是图结构就很复杂了),树结构的特点就是,一号玩家一开始选定的那个节点,会把整棵树分成3个区间,父节点的区间,左子树的区间,右子树的区间,这3个区间互不相通。
于是问题简单化了,二号玩家就是要去堵一号玩家的路,于是问题又简化成了,这3个区间,哪个区间的节点数目最多,如果数目能超过整个树一半的节点数目,二号玩家就选择这个区间,就赢了。
AC代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int>edge[105];int dfs(TreeNode* root){if(root->left!=NULL){int left = dfs(root->left);edge[root->val].push_back(left);edge[left].push_back(root->val);}if(root->right!=NULL){int right = dfs(root->right);edge[root->val].push_back(right);edge[right].push_back(root->val);}return root->val;}queue<int>q;bool vis[105];int bfs(int u, int x){memset(vis,0,sizeof(vis));vis[u] = true;vis[x] = true;q.push(u);int ans = 0;while(!q.empty()){int u = q.front();q.pop();ans += 1;for(int i=0;i<edge[u].size();i++){int v = edge[u][i];if(vis[v])continue;vis[v] = true;q.push(v);}}return ans;}bool btreeGameWinningMove(TreeNode* root, int n, int x) {dfs(root);for(int i=0;i<edge[x].size();i++){int u = edge[x][i];int ans = bfs(u, x);if(ans>int(n/2))return true;}return false;}
};

相关文章:

LeetCode 1145. 二叉树着色游戏 -- 简单搜索
二叉树着色游戏 提示 中等 199 相关企业 有两位极客玩家参与了一场「二叉树着色」的游戏。游戏中,给出二叉树的根节点 root,树上总共有 n 个节点,且 n 为奇数,其中每个节点上的值从 1 到 n 各不相同。 最开始时: 「一…...

HyperGBM的三种Early Stopping方式
本文作者:杨健,九章云极 DataCanvas 主任架构师 很多机器学习框架如都提供了Early Stopping策略,主要用来防止模型过拟合。和模型训练提前停止的目标不同,AutoML的Early Stopping策略更多考虑的是算力消耗和模型质量的平衡。 通…...
心系区域发展,高德用一体化出行服务平台“聚”力区域未来
交通,是城市的血脉。通过对人、资源、产业的连接,交通建设往往是城市和区域经济发展的前提。不过,在度过了“要想富,先修路”的初级建设阶段后,交通产业内部也出现了挑战,诸如城市秩序、发展成本、用户使用…...
AI画图_stable-diffusion-webui安装使用指南(1)
本文章适用于: 有一定学习能力和钻研能力,遇到问题能合理使用搜索引擎尝试解决问题的人想在windows系统中尝试使用AI作画工具stable-diffusion-webui进行绘画的人有一定的计算机基础(会魔法上网、知道 python和Git)和英文阅读能力的人显卡为…...
浅谈MySQL主从复制
目录 1.MySQL主从复制是什么 2.MySQL主从复制的意义 3.MySQL主从复制原理 4.数据同步一致性问题 5.实现方式 1.MySQL主从复制是什么 MySQL主从复制就是指数据可以从一台MySQL的主节点复制到一个或多个从节点。 MySQL默认采用异步复制方式,这样从节点不用一直访…...
docker-compose安装kafka和php简单测试
docker-compose.yml内容: version: 3.1 services: zookeeper: container_name: zookeeper image: zookeeper:3.6 ports: - 2181:2181 kafka: image: wurstmeister/kafka container_name: kafka depends_on: - zookeeper …...

【蓝桥云课】快速幂
问题描述:快速求aba^bab 方法一:常规方法相乘a∗a∗a∗a∗...∗aa*a*a*a*...*aa∗a∗a∗a∗...∗a 方法二:分治方法求aba^bab ab{1,b0a,b1ab2⋅ab2,b为偶数ab−12⋅ab12,b为奇数a^b\begin{cases} 1& \text{,b0}\\ a& \text{,b1}\\ a…...
解决windows安装wxPython安装失败、速度过慢及PyCharm上wx包爆红问题
网上关于wxPython安装失败,安装速度过慢,以及安装成功后PyCharm中import wx仍然爆红的文章有很多,也特别杂,解决起来特别困难,今天在这里对问题的处理进行一个整合,希望能帮助到大家。 安装wxPython这里运用…...

封装小程序request请求[接口函数]
在这篇小程序API的Promise化文章中讲到小程序官方提供的异步API都是基于回调函数来实现的,在大量的使用这种回调函数就会造成回调地狱的问题,以及代码的可读性和可维护性差,通过对小程序API的Promise化能解决,那么本篇是来讲进行对…...

嵌入式 STM32 通讯协议--MODBUS
目录 一、自定义通信协议 1、协议介绍 2、网络协议 3、自定义的通信协议 二、MODBUS通信协议 1、概述 2、MODBUS帧结构 协议描述 3、MODBUS数据模型 4、MODBUS事务处理的定义 5、MODBUS功能码 6、功能码定义 7、MODBUS数据链路层 8、MODBUS地址规则 9、MO…...

互联网人看一看,这些神器你用过哪些?
很多小伙伴在剪辑视频的过程中经常可以看到一些语音素材,经常刷视频的小伙伴也可以看到很多视频中经常出现一些AI合成的声音或者音效,这些配音可以给视频增添很多亮点!那么大家都是怎么将文字转语音的呢?今天给大家分享5款非常专业…...
Kotlin学习:5.2、异步数据流 Flow
Flow一、Flow1、Flow是什么东西?2、实现功能3、特点4、冷流和热流5、流的连续性6、流的构建器7、流的上下文8、指定流所在协程9、流的取消9.1、超时取消9.2、主动取消9.3、密集型任务的取消10、背压和优化10.1、buffer 操作符10.2、 flowOn10.3、conflate 操作符10.…...
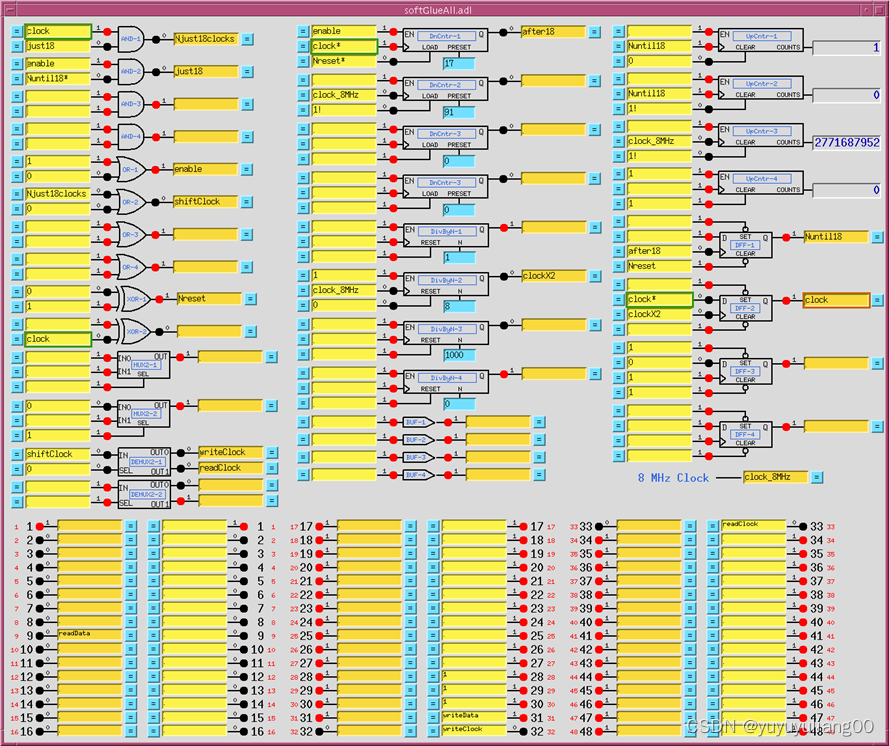
EPICS synApps介绍
一、synApps是什么? 1) 一个用于同步束线用户的EPICS模块集合。 2) EPICS模块 alive, autosave, busy, calc, camac, caputRecorder, dac128V, delaygen, dxp, ip, ip330, ipUnidig, love, mca, measComp, modbus, motor, optics, quadEM,…...
Pycharm和跳板机 连接内网服务器
Pycharm和跳板机 连接内网服务器 建立配置文件 本地配置 .ssh 文件夹下配置 config 文件 Host jumpHostName xxxPort 22User xxxServerAliveInterval 30IdentityFile C:\Users\15284\.ssh\id_rsa # 通过密钥连接Host server # 同样,任意名字,随…...
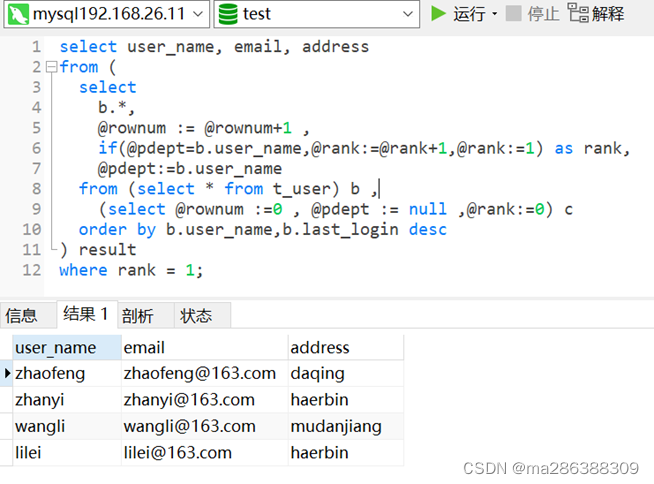
mysql去重查询的三种方法
文章目录前言一、插入测试数据二、剔除重复数据方法1.方法一:使用distinct2.方法二:使用group by3.方法三:使用开窗函数总结前言 数据库生成环境中经常会遇到表中有重复的数据,或者进行关联过程中产生重复数据,下面介…...

PHP反序列化
文章目录简介POP链构造和Phar://题目[CISCN2019 华北赛区 Day1 Web1]Dropbox字符串逃逸简介 php序列化的过程就是把数据转化成一种可逆的数据结构,逆向的过程就叫做反序列化。 php将数据序列化和反序列化会用到两个函数: serialize 将对象格式化成有序的…...

什么蓝牙耳机打电话效果最好?通话效果好的无线蓝牙耳机
2023年了,TWS耳机虽说近乎人手一只了,但用户换新的需求和呼声依然热火朝天,因为我们想要听音乐、刷视频的时候都得准备,下面整理一些通话效果不错的耳机品牌。 第一款:南卡小音舱蓝牙耳机 动圈单元:13.3m…...

Tesseract centos环境安装,基于springboot图片提取文字
下载tesseract-orc https://github.com/tesseract-ocr/tesseract/tags下载leptonica wget http://www.leptonica.org/source/leptonica-1.78.0.tar.gz解压leptonica tar -xvf leptonica-1.78.0.tar.gz 配置编译安装leptonica 进文件夹 ./configure make make install安装aut…...

Elasticsearch7.8.0版本优化——写入速度优化
目录一、 写入速度优化的概述二、如何写入速度优化2.1、 批量数据提交2.2、 优化存储设备2.31、 合理使用合并2.4、 减少 Refresh2.5、 加大 Flush2.6、 减少副本的数量一、 写入速度优化的概述 ES 的默认配置,是综合了数据可靠性、写入速度、搜索实时性等因素。实使…...
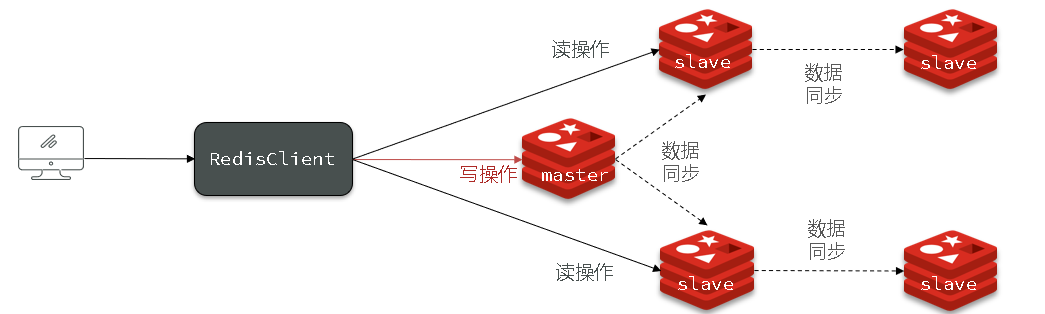
【Redis】Redis主从同步中数据同步原理
【Redis】Redis主从同步中数据同步原理 文章目录【Redis】Redis主从同步中数据同步原理1. 全量同步1.1 判断是否第一次数据同步2. 增量同步3. 优化Redis主从集群4. 总结1. 全量同步 主从第一次同步是全量同步。 数据同步包括以下三个阶段: 在从节点执行slaveof命令…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...
