离散数学---期末复习知识点
一、 数理逻辑
[复习知识点]
1、命题与联结词(否定¬、析取∨、合取∧、蕴涵→、等价↔),命题(非真既假的陈述句),复合命题(由简单命题通过联结词联结而成的命题)
2、命题公式与赋值(成真、成假),真值表,公式类型(重言、矛盾、可满足),公式的基本等值式

3、范式:析取范式、合取范式,极大(小)项,主析取范式、主合取范式
4、公式类型的判别方法:真值表法、等值演算法、主析取/合取范式法
5、命题逻辑的推理理论


6、谓词、量词、个体词(公式一阶逻辑3要素)、个体域、变元(约束出现与自由出现)
7、命题符号化、谓词赋值与解释,谓词公式的类型(永真、永假、可满足)
8、谓词公式的等值式(代换实例、消去量词、量词否定和量词辖域收与扩、量词分配)和置换规则(置换规则、换名规则)
9、一阶逻辑前束范式(定义、求法)
本章重点内容:命题与联结词、公式与解释、(主)析取范式与(主)合取范式、公式类型的判定、命题逻辑的推理、谓词与量词、命题符号化、谓词公式赋值与解释、求前束范式。
[复习要求]
1、理解命题的概念;了解命题联结词的概念;理解用联结词产生复合命题的方法。
2、理解公式与赋值的概念;掌握求给定公式真值表的方法,用基本等值式化简其它公式,公式在解释下的真值。
3、了解析取(合取)范式的概念;理解极大(小)项的概念和主析取(合取)范式的概念;掌握用基本等值式或真值表将公式化为主析取(合取)范式的方法。
4、掌握利用真值表、等值演算法和主析取/合取范式的唯一性判别公式类型和公式等价方法。
5、掌握命题逻辑的推理理论。
6、理解谓词、量词、个体词、个体域、变元的概念;理解用谓词、量词、逻辑联结词描述一个简单命题;掌握命题的符号化。
7、理解公式与解释的概念;掌握在有限个体域下消去公式量词,求公式在给定解释下真值的方法;了解谓词公式的类型。
8、掌握求一阶逻辑前束范式的方法。
二、 集 合
[复习知识点]
1、集合、元素、集合的表示方法(列元素法、谓词表示法)、子集、空集、全集、集合的包含、相等、幂集
2、集合的交、并、差、补以及对称差等运算及有穷集的计数(文氏(Venn)图、包含排斥原理)
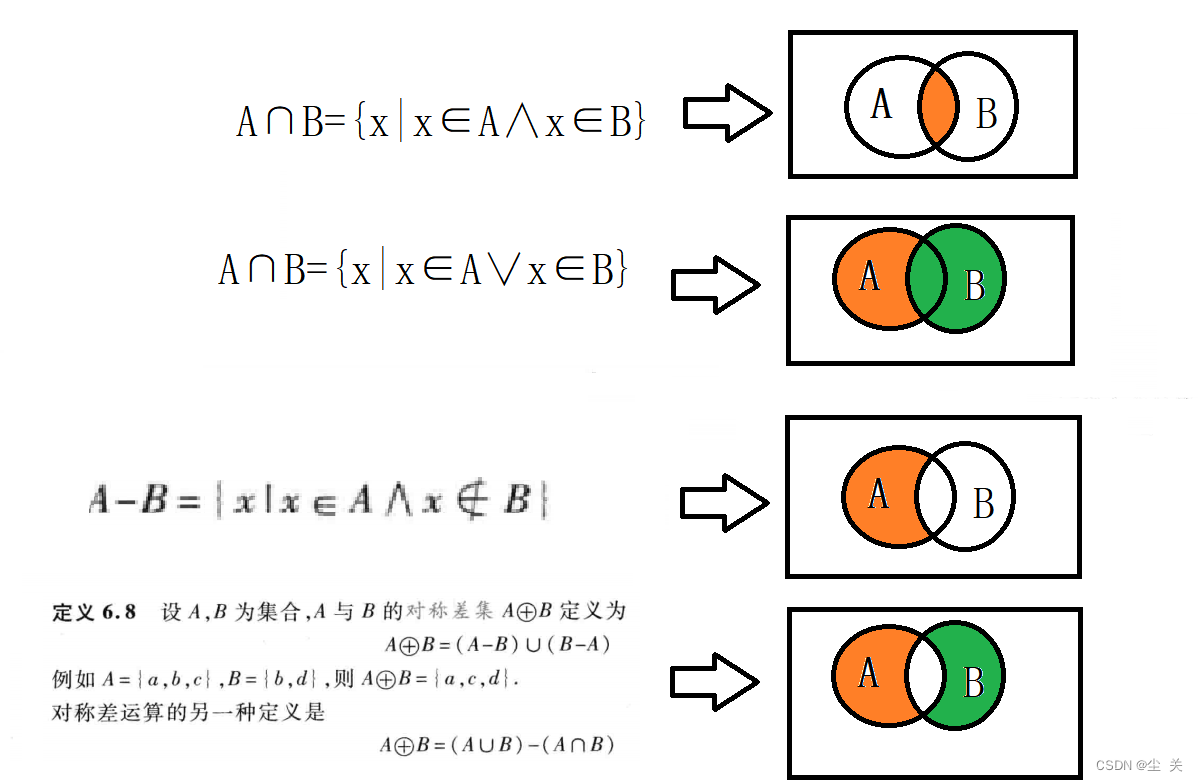
3、集合恒等式(幂等律、交换律、结合律、分配律、吸收律、矛盾律、德摩根律等)及应用

本章重点内容:集合的概念、集合的运算性质、集合恒等式的证明。
[复习要求]
三、 二元关系
[复习要求]
1、了解序偶与笛卡尔积的概念,掌握笛卡尔积的运算。
2、理解关系的概念:二元关系、空关系、全域关系、恒等关系;掌握关系的集合表示、关系矩阵和关系图、关系的运算。】



3、掌握求复合关系与逆关系的方法。
4、理解关系的性质(自反性、反自反性、对称性、反对称性、传递性),掌握其判别方法(定义、图)。
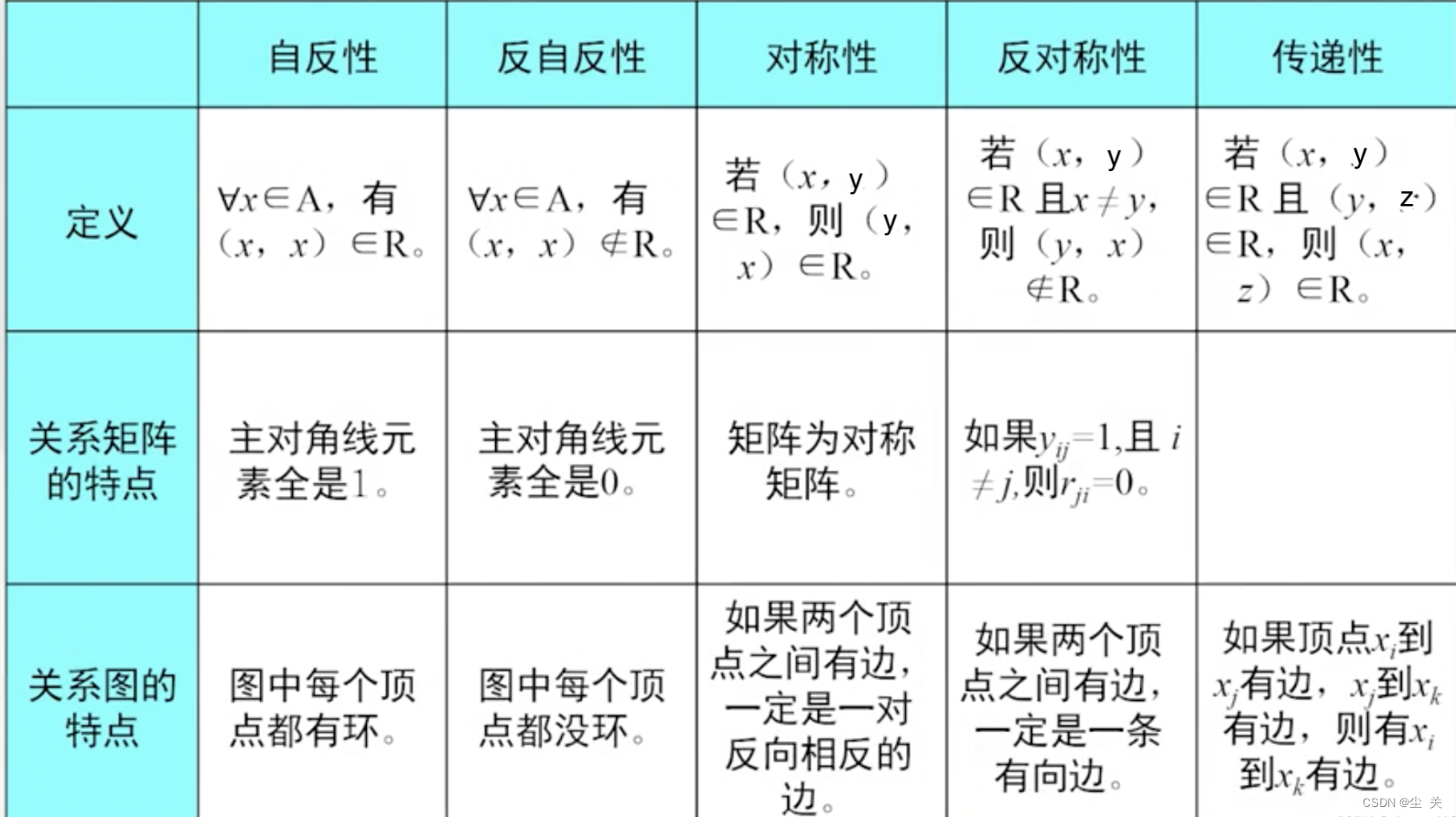
自反性:全部顶点均有环;反自反性:全部顶点均无环;对称性:有边均双边(无单边,顶点有无环不影响) ;反对称性:有边均单边(顶点有无环不影响)(无平行边)
传递性:a到b有边,b到c有边,则a到c也有边,否则不然。
5、掌握求关系的闭包 (自反闭包、对称闭包、传递闭包)的方法。

换言之:r=加自环 s=单边变双边 t:努力变传递
6.理解等价关系和划分、掌握等价类和划分的求法
7、理解偏序关系的概念,掌握画哈斯图的方法,极大/小元、最大/小元的求法。
相关概念:



哈斯图的方法:

如图7.7:5,9,6,8,7均是极大元,1是极小元,无最大元,最小元为1;右边: {a,b,c}是极大元,∅是极小元,最大元是 {a,b,c},最小元为∅
四、函数
[复习知识点]
- 理解函数概念:函数、函数相等、A到B的函数。

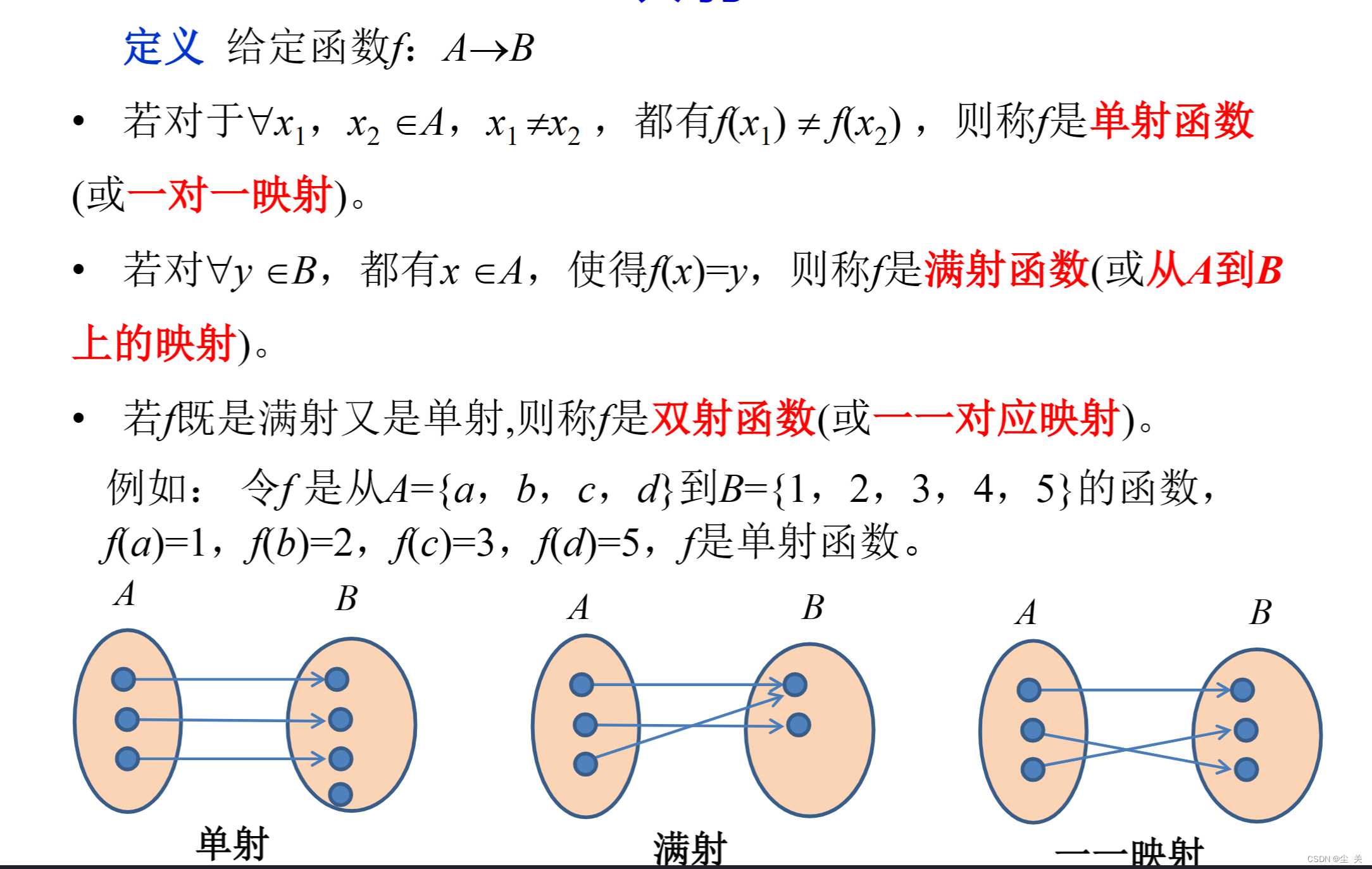
2、理解单射、满射、双射等概念,掌握其判别方法。
单射:不同的x所对应的y不同。
满射:y的值域全用到了。
双射:单+满
3、函数的复合与反函数
函数复合及相关联习

 反函数:
反函数:
本章重点内容:函数的定义及判别方法、函数的三大性质、函数的复合与反函数。
[复习要求]
- 掌握函数及从A到B的函数的判别方法。
函数:
从A到B的函数:

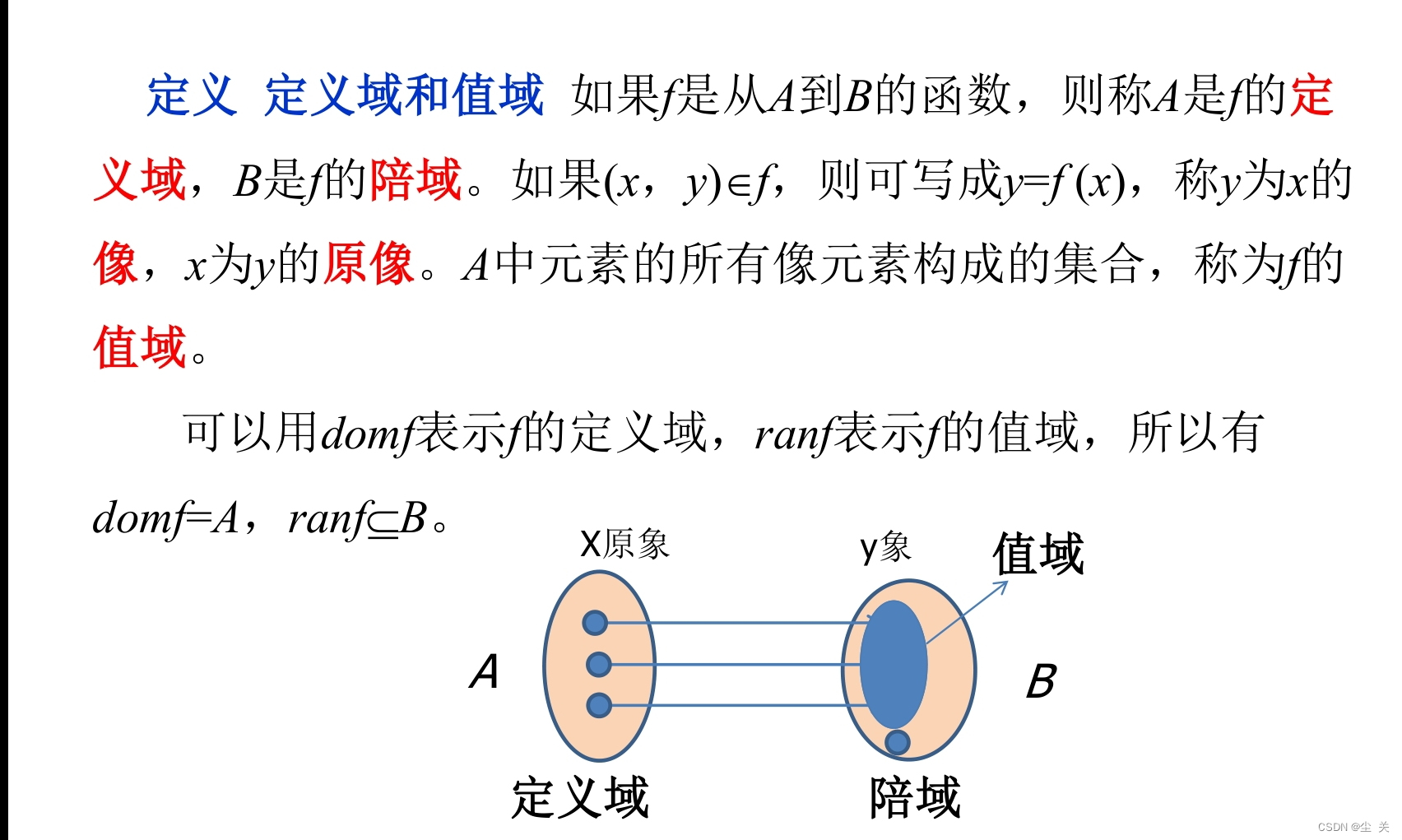
2、理解函数的像与原像。
3.掌握函数的单射、满射、双射的判别方法。
4、掌握求函数的复合与反函数的方法。

五、 图论
[复习知识点]
1、 图的基本概念:无向图与有向图(根据联结的边是否有方向)、顶点与边的关联关系、顶点(边)与顶点(边)之间邻接关系、简单图与多重图、顶点度数(度)与握手定理、图的同构、完全图、子(补)图。
度:
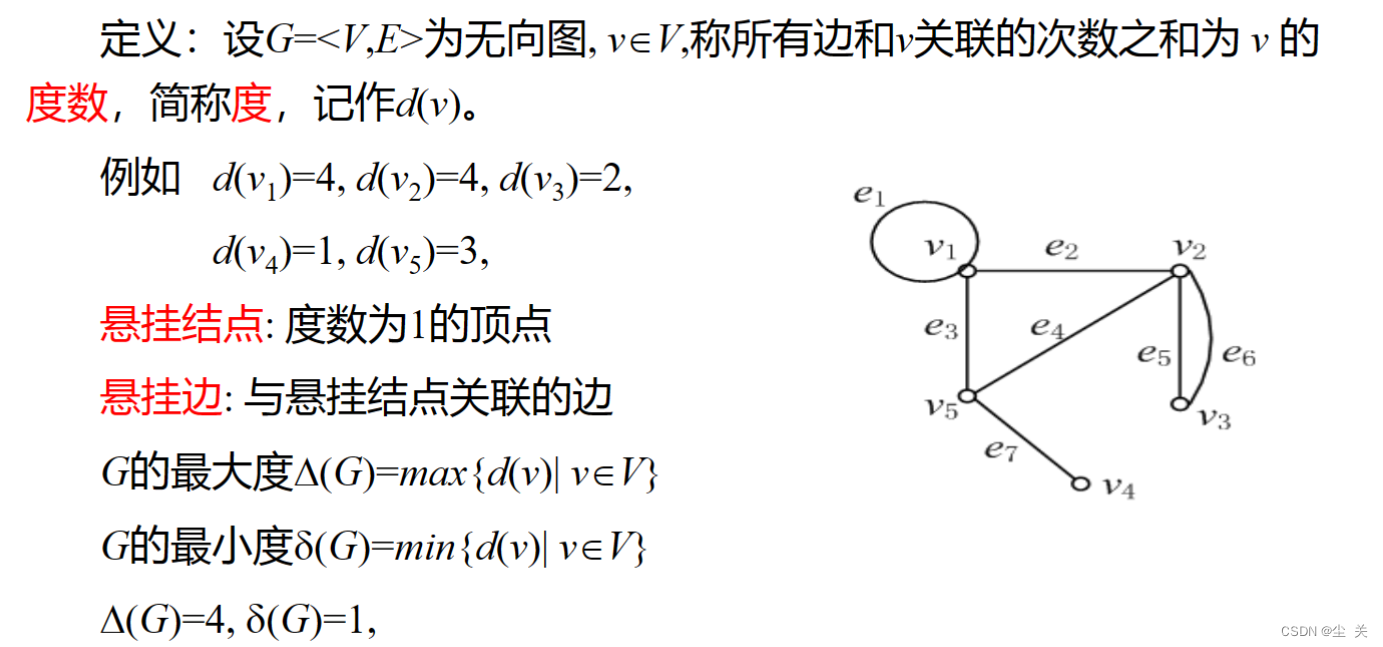

握手定理:
简单图与多重图:
2、 通路与回路、简单通(回)路与初级通(回)路;连通图与非连通图、连通分支、点割集、边割集、点(边)连通度;强连通图、单向连通图与弱连通图;二部图。
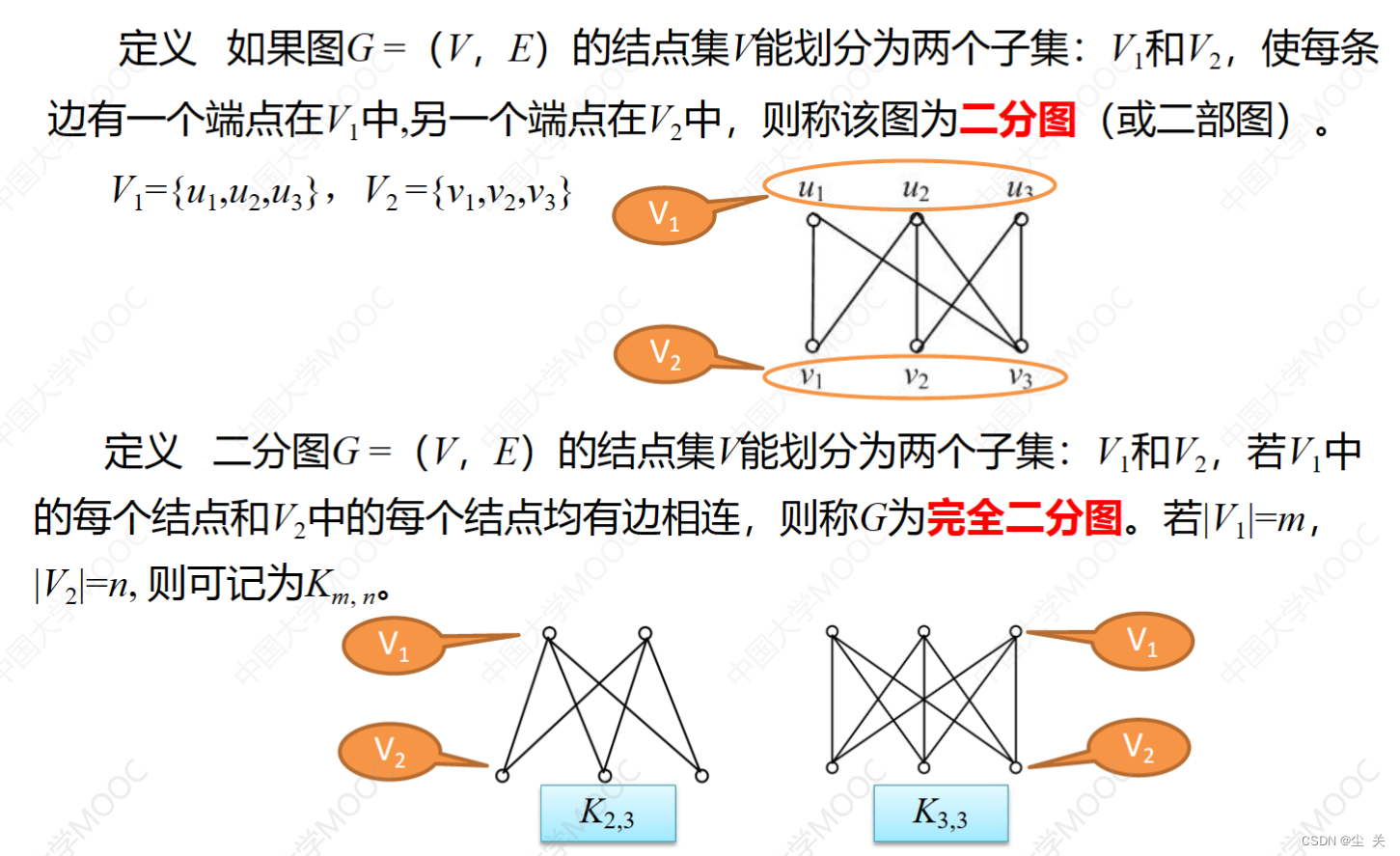
3、 图的矩阵表示:关联矩阵、邻接矩阵、可达矩阵。
4、 欧拉通(回)路、(半)欧拉图;哈密尔顿通(回)路、(半)哈密尔顿图;

5、 无向树、生成树、带权树、最小生成树。
6、 有向树、树根、有序树、二叉树、最优二叉树、前缀码、最佳前缀码、霍夫曼(Huffman)算法、二叉树的周游及应用。
本章重点内容: 握手定理、点(边)割集、通路与回路、特殊图(欧拉图与哈密顿图、无(有)向树)、最优二叉树、最佳前缀码、霍夫曼(Huffman)算法。
[复习要求]
1、理解图的有关概念:图、完全图、简单图、子图、母图、生成子图等。
2、深刻理解握手定理及其推论的内容,并能熟练地应用它们。
3、能判断两个图是否同构。
4、理解连通度、点割集、边割集、割边和割点。
5、能判断图是否为强连通图、单向连通图与弱连通图。
6、理解图的矩阵表示(关联矩阵、相邻矩阵)和性质以及熟练掌握用有向图的邻接矩阵及各次幂求图中通路与回路数的方法。
4、理解欧拉图、哈密顿图的定义及判别定理。在无向图中找出一条欧拉通路或欧拉回路、哈密顿通路或哈密顿回路。
5、理解无向树的定义,熟练掌握无向树的主要性质,并能灵活应用它们。
6、理解生成树的有关概念与性质。
7、理解有向树、根树、二叉树和前缀码的有关概念;掌握用霍夫曼(Huffman)算法求带权图的最优二分树,掌握求最佳前缀码方法,二叉树的中序和前序行遍法。
相关文章:

离散数学---期末复习知识点
一、 数理逻辑 [复习知识点] 1、命题与联结词(否定¬、析取∨、合取∧、蕴涵→、等价↔),命题(非真既假的陈述句),复合命题(由简单命题通过联结词联结而成的命题) 2、命题公式与赋值(成真、成假)&#x…...

在线安装ESP32和ESP8266 Arduino开发环境
esp32和esp8266都是乐鑫科技开发的单片机产品,esp8266价格便宜开发板只需要十多块钱就可以买到,而esp32是esp8266的升级版本,比esp8266的功能和性能更强大,开发板价格大约二十多元就可以买到。 使用Arduino开发esp32和esp8266需要…...

【Python实战】激情澎湃,2023极品劲爆舞曲震撼全场,爬虫一键采集DJ大串烧,一曲醉人女声DJ舞曲,人人都听醉~(排行榜采集,妙啊~)
导语 哈喽!大家好。我是木木子吖~今天给大家带来爬虫的内容哈。 所有文章完整的素材源码都在👇👇 粉丝白嫖源码福利,请移步至CSDN社区或文末公众hao即可免费。 今天教大家Python爬虫实战一键采集大家喜欢的DJ舞曲哦! …...

[SSD综述 1.5] SSD固态硬盘参数图文解析_选购固态硬盘就像买衣服?
版权声明:付费作品,未经许可,不可转载前言SSD (Solid State Drive),即固态硬盘,通常是一种以半导体闪存(NAND Flash)作为介质的存储设备。SSD 以半导体作为介质存储数据&…...
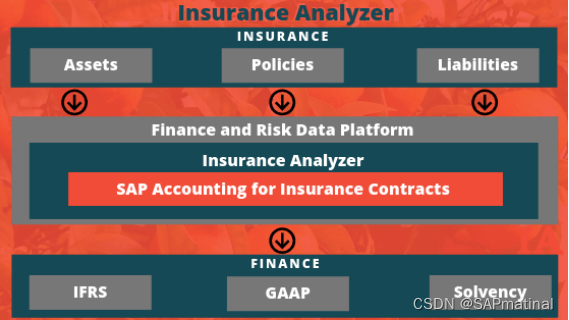
SAP Insurance Analyzer
SAP Insurance Analyzer 是一款用于保险公司财务和风险管理的软件。SAP Insurance analyzer 支持基于 IFRS 17 或 Solvency II 的保险合同估值和计算要求。SAP Insurance Analyzer 于 2013 年 5 月推出,为源数据和结果数据集成了一个预配置的保险数据模型。 源数据…...

自动化测试 ——自动卸载软件
在平常的测试工作中,经常要安装软件,卸载软件, 即繁琐又累。 安装和卸载完全可以做成自动化。 安装软件我们可以通过自动化框架,自动点击Next,来自动安装。 卸载软件我们可以通过msiexec命令行工具自动化卸载软件 用msiexec 命令来卸载软件 …...

05 封装
在对 context 的封装中,我们只是将 request、response 结构直接放入 context 结构体中,对应的方法并没有很好的封装。 函数封装并不是一件很简单、很随意的事情。相反,如何封装出易用、可读性高的函数是非常需要精心考量的,框架中…...

clean
clean code 记得以前写过这题,写的乱七八糟,分析来分析去。 后悔应该早点写代码,leetcode大一就该刷了。 https://leetcode.cn/problems/plus-one/submissions/ class Solution { public:vector<int> plusOne(vector<int>&…...

佛科院计算机软件技术基础——线性表
一、基础知识了解:结构体的理解:我们知道整型是由1位符号位和15位数值位组成,而就可以把结构体理解为我们定义的数据类型,如:typedef struct {int data[2]; //存储顺序表中的元素int len; …...

linux下终端操作mysql数据库
目录 一.检查mysql是否安装 1. 查看文件安装路径 2. 查询运行文件所在路径(文件夹地址) 二.登录mysql 三.列出mysql全部用户 四.常用指令 1.查看全部数据库 2.选择数据库 …...

MySQL参数优化之thread_cache_size
1.thread_cache_size简介 每建立一个连接,都需要一个线程来与之匹配,此参数用来缓存空闲的线程,以至不被销毁,如果线程缓存中有空闲线程,这时候如果建立新连接,MYSQL就会很快的响应连接请求。 show statu…...
:gRPC健康检查协议详解)
gRPC服务健康检查(二):gRPC健康检查协议详解
gRPC健康检查协议健康检查用于检测服务端能否正常处理rpc请求,客户端对服务端的健康检查可以点对点进行,也可以通过某些控制系统(如负载平衡)进行。客户端可以根据服务端返回的状态执行对应的策略。因为GRPC服务可以用于简单的客户…...
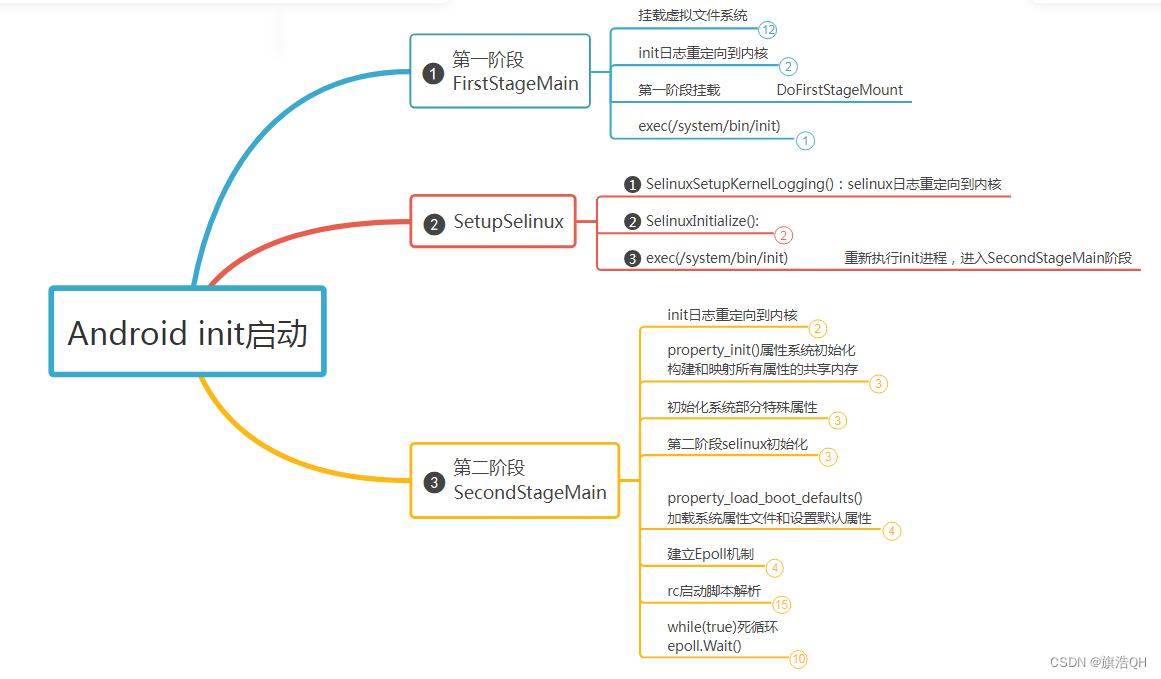
Android系统10 RK3399 init进程启动(四十七) Android init 进程整体代码逻辑简述
配套系列教学视频链接:安卓系列教程之ROM系统开发-百问100ask说明系统:Android10.0设备: FireFly RK3399 (ROC-RK3399-PC-PLUS)前言本文简单描述一下android init祖先进程启动的基本执行流程,让大家有一个整…...

CSDN 编程竞赛三十二期题解
竞赛总览 CSDN 编程竞赛三十二期:比赛详情 (csdn.net) 竞赛题解 题目1、传奇霸业 传奇霸业,是兄弟就来干。小春(HP为a)遇到了一只黄金哥布林(HP为x)。小春每次能对哥布林造成b点伤害,哥布林…...

Kubernetes 中的 Pod Hook
Pod Hook 我们知道Pod是Kubernetes集群中的最小单元,而 Pod 是有容器组组成的,所以在讨论 Pod 的生命周期的时候我们可以先来讨论下容器的生命周期。 实际上 Kubernetes 为我们的容器提供了生命周期钩子的,就是我们说的Pod Hook,…...
Linux操作系统安装MySQL(rpm安装)
Linux操作系统安装MySQL(rpm安装)1 背景2 环境说明3 准备工作3.1 端口查看3.2 检查安装3.3 创建MySQL用户和组4 MySQL安装4.1 下载MySQL4.2 解压安装包4.3 安装MySQL4.4 初始化MySQL4.5 启动MySQL4.6 设置MySQL初始密码4.6.1 查看数据库初始密码4.6.2 更…...
MySQL高级第二讲
目录 二、MySQL高级02 2.1 触发器 2.1.1 触发器介绍 2.1.2 创建触发器 2.2 MySQL的体系结构 2.3 存储引擎 2.3.1 存储引擎概述 2.3.2 各种存储引擎特性 2.3.3 InnoDB 2.3.4 MyISAM 2.3.5 MEMORY 2.3.6 MERGE 2.3.7 存储引擎的选择 2.4 优化sql 2.4.1 查看sql执行…...

凸优化专题1
多变量函数的求导与求梯度/矩阵求导 1. 导数 定义: 设f:Rn→Rm,且x∈intdomf,则f在点x的导数(或称Jacobian)记为矩阵Df(x)∈Rmnf:\R^n \rightarrow \R^m, 且x\in \mathbf{int}\ \mathbf{dom} f, 则f 在点x的导\\数(或称Jacobian)记为矩阵 Df(x) \in \R^{m\times n}f:Rn→Rm,且…...
【蓝桥杯每日一题】递推算法
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙我与杀戮之中绽放,亦如黎明的花…...
Unity性能优化: 性能优化之内存篇
前言 本文和传统的内存优化不一样,不是讲如何降低内存占用,而是讲编程开发中要注意的内存问题以及一些内存技术的演变与原理。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀 1: Application进程…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
