二分查找——34. 在排序数组中查找元素的第一个和最后一个位置

文章目录
- 1. 题目
- 2. 算法原理
- 2.1 暴力解法
- 2.2 二分查找
- 左端点查找
- 右端点查找
- 3. 代码实现
- 4. 二分模板
1. 题目
题目链接:34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
2. 算法原理
2.1 暴力解法
这里暴力解法也比较简单,直接遍历整个数组,记录第一次出现的位置和最后一次出现的位置,时间复杂度为O(N),这里就不示例了。
2.2 二分查找
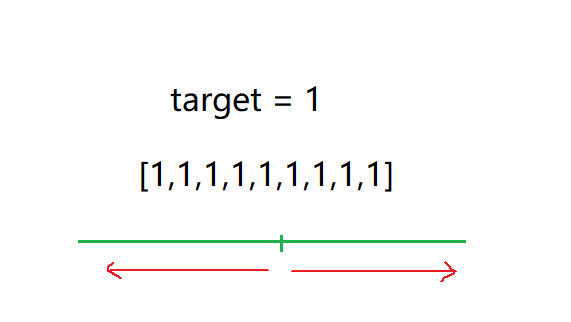
这里是不能够直接二分的,直接二分我们还需要从中间再往两边搜索,如果该数组里面的值全是目标值,效率就会降为O(N)。
这里还是利用二段性,我们可分开查找左右端点,分两种情况即可:
左端点查找
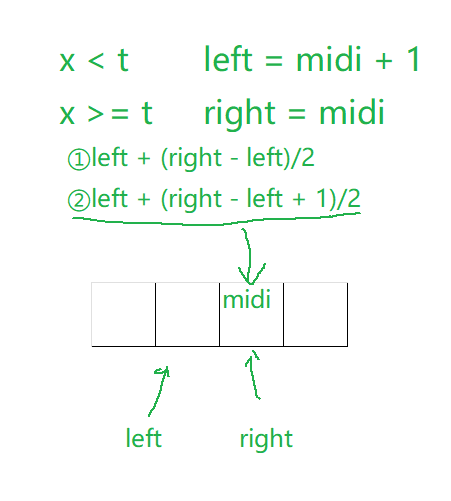
这里我们的判断条件是:nums[midi] < target和nums[midi] >= target
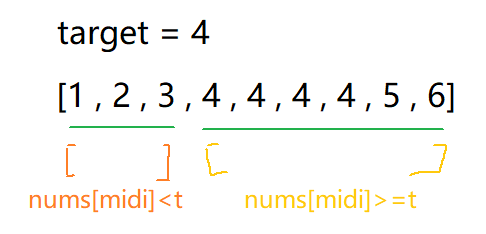
当
midi落在左区间的的时候,肯定是没有我们要寻找的值的,我们让left = midi+1即可当
midi落在右区间的时候,这个区域里面是有可能有我们的target,不能让right = midi - 1,这样会导致错失我们的target,所以直接让right = midi即可
细节处理
循环条件:
left < right
这里一共就三种情况有目标值、全是大于目标值、全是小于目标值
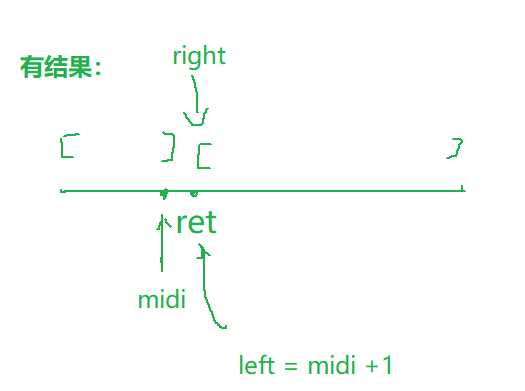
有结果:
left一直在不符合条件的区间移动;right一直在符合条件的区间移动,且不会超出这个区间
letf要执行,每次都是执行的midi+1,所以当left跳出去的时候,正好是在目标值处所以
left == right时,就是最终结果,无需判断
全是大于
target:在次情况下,左区间的条件一直都不会命中,而right,则一直在向left这边移动,最后相遇的时候,我们只需判断相遇处是不是target全是小于
target:这个情况就和上面这个一样如果我们在
left == right的时候判断了,那么就会进入死循环,无限命中右区间条件求中点:
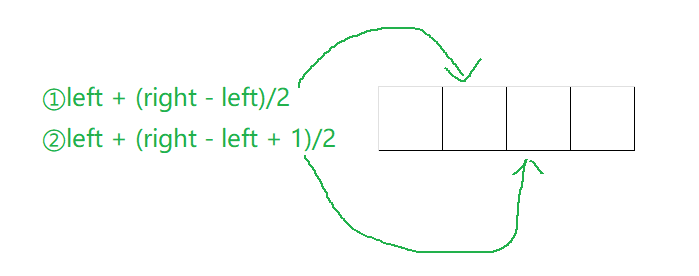
midi = left + (right - left)/2
我们求中点的时候采用left+(right-left)/2这里是防止溢出,这种与left+(right-left+1)/2的区别就是当数组为偶数的时候,前者求的是靠左位置,而后者是靠右位置
这个在普通二分是没什么影响的,可是在我们求端点的时候,进行最后一次操作:
采用②求中点时,命中右区间的条件,则会陷入死循环
右端点查找
查找右端点和查找左端点思想一致
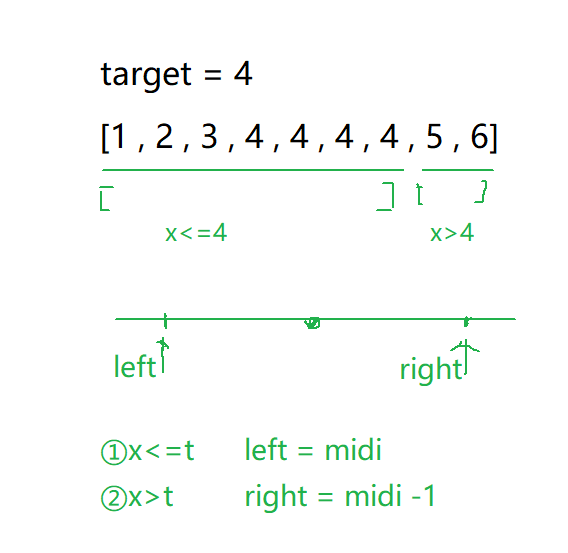
这个求中点的方式就采用left+(right-left+1)/2靠右位置
3. 代码实现
class Solution
{
public:vector<int> searchRange(vector<int>& nums, int target){//检查空数组if(nums.size() == 0) return {-1,-1};int left = 0;int right = nums.size()-1;int begin = left;//查找左端点while(left < right){int midi = left+(right-left)/2;if(nums[midi]<target){left = midi+1;}else right = midi;}//判断是否有结果if(nums[left] != target) return {-1,-1};else begin = left; //记录左端点//查找右端点//left = 0; //可不用重置right = nums.size()-1;while(left<right){int midi = left+(right-left+1)/2;if(nums[midi]<=target){left = midi;}else right = midi-1;}return {begin,right};}
};
4. 二分模板
查找区间左端点:
while(left<right)
{int mid = left + (right -left)/2;if(...){left = mid + 1;}else{right = mid;}
}
查找区间右端点:
while(left<right)
{int mid = left + (right -left+1)/2;if(...){left = mid;}else{right = mid - 1;}
}
当下面出现减肥的时候,上面就用加一
相关文章:

二分查找——34. 在排序数组中查找元素的第一个和最后一个位置
文章目录 1. 题目2. 算法原理2.1 暴力解法2.2 二分查找左端点查找右端点查找 3. 代码实现4. 二分模板 1. 题目 题目链接:34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode) 给你一个按照非递减顺序排列的整数数组 nums&#…...

MFC中的主窗口以及如何通过代码找到主窗口
MFC程序中的主窗口 在MFC程序中,可以设置主窗口,主窗口在应用程序类中设置,即设置应用程序类(通常以App结尾,通常包括InitInstance方法的类)的m_pMainWnd属性,将其设置为主窗口的指针。 一般在…...
图文详解)
Typora下载安装 (Mac和Windows)图文详解
目录 Windows版本 一、下载 二、安装 Mac版本 一、下载 二、安装...
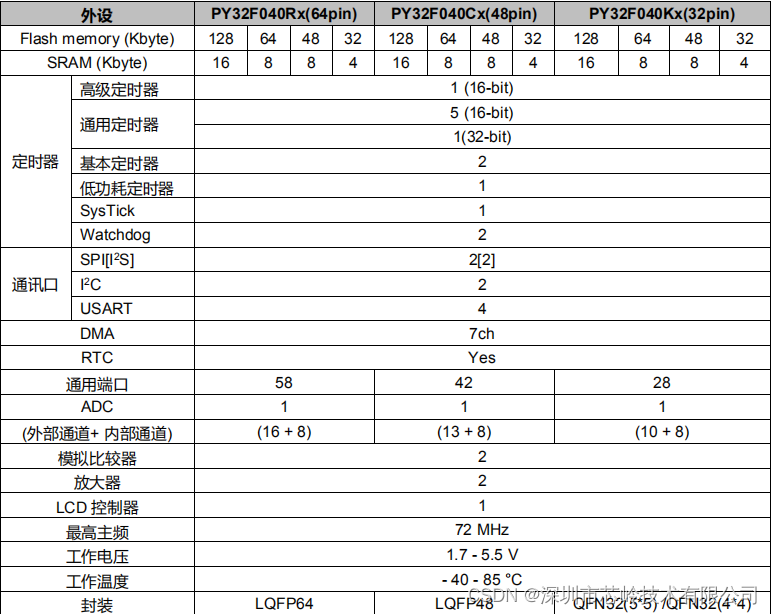
32位单片机PY32F040,主频72M,外设丰富,支持断码LCD
PY32F040 系列微控制器采用高性能的 32 位 ARM Cortex-M0 内核,宽电压工作范围的 MCU。嵌入高达 128 Kbytes flash 和 16 Kbytes SRAM 存储器,最高工作频率 72 MHz。LQFP64封装两块出头就可以拿到,我们还有开发板和开发资料帮助客户更好的开发。 PY32F040 系列微控…...
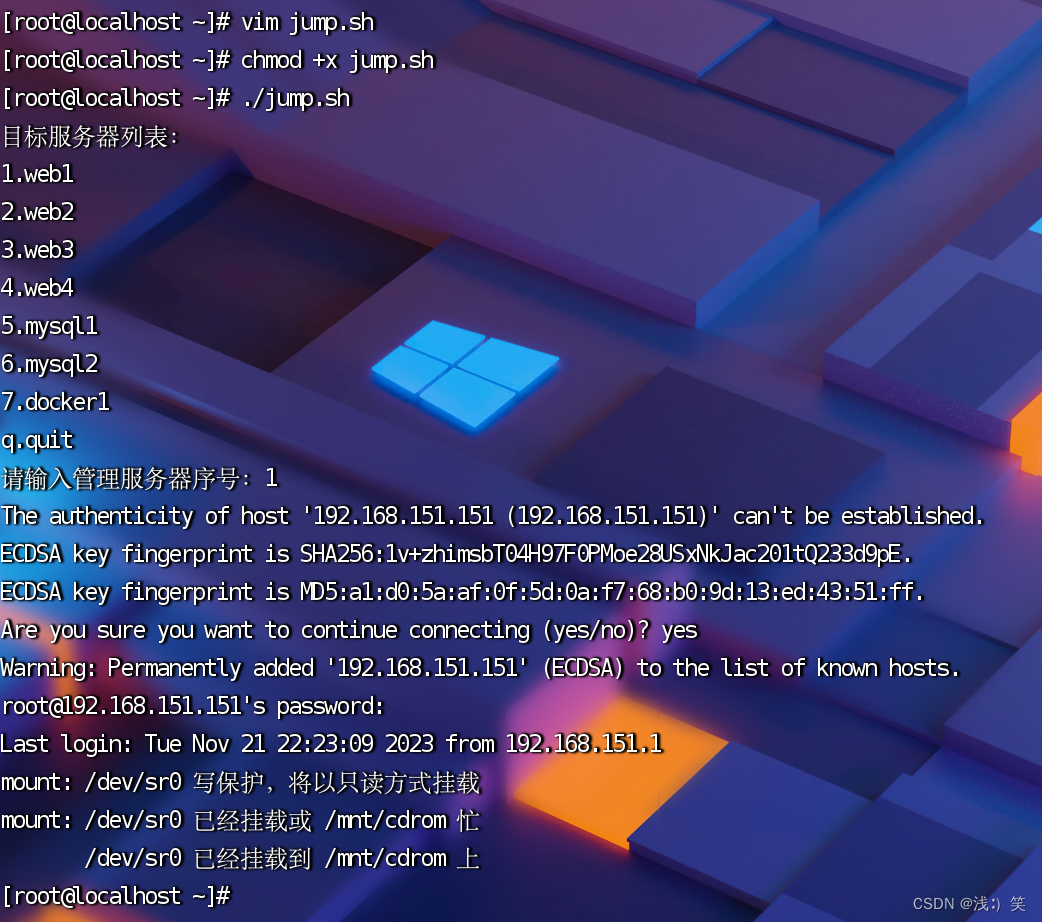
Shell判断:模式匹配:case(二)
简单的JumpServer 1、需求:工作中,我们需要管理N多个服务器。那么访问服务器就是一件繁琐的事情。通过shell编程,编写跳板程序。当我们需要访问服务器时,看一眼服务器列表名,按一下数字,就登录成功了。 2、…...
从android.graphics.Path中取出Point点,Kotlin
从android.graphics.Path中取出Point点,Kotlin /*** 从一条Path中获取多少个Point点*/private fun getPoints(path: Path, pointCount: Int): Array<FloatPoint?> {val points arrayOfNulls<FloatPoint>(pointCount)val pm PathMeasure(path, false)…...

力扣C++学习笔记——C++ 给vector去重
要使用std::set对std::vector进行去重操作,您可以将向量中的元素插入到集合中,因为std::set会自动去除重复元素。然后,您可以将集合中的元素重新存回向量中。以下是一个示例代码,演示如何使用std::set对std::vector进行去重&#…...

Flutter笔记:使用相机
Flutter笔记 使用相机 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/134493373 【简介】本文介绍在 Fl…...

包装类型的缓存机制
Java 基本数据类型的包装类型的大部分都用到了缓存机制来提升性能。 Byte,Short,Integer,Long 这 4 种包装类默认创建了数值 [-128,127] 的相应类型的缓存数据,Character 创建了数值在 [0,127] 范围的缓存数据,Boolean 直接返回 True or Fal…...

【BUG】第一次创建vue3+vite项目启动报错Error: Cannot find module ‘worker_threads‘
问题描述 第一次创建vue3vite项目启动报错如下: Error: Cannot find module worker_threadsat Function.Module._resolveFilename (internal/modules/cjs/loader.js:636:15)at Function.Module._load (internal/modules/cjs/loader.js:562:25)at Module.require (…...
多目标应用:基于非支配排序的鲸鱼优化算法NSWOA求解微电网多目标优化调度(MATLAB代码)
一、微网系统运行优化模型 微电网优化模型介绍: 微电网多目标优化调度模型简介_IT猿手的博客-CSDN博客 二、基于非支配排序的鲸鱼优化算法NSWOA 基于非支配排序的鲸鱼优化算法NSWOA简介: 三、基于非支配排序的鲸鱼优化算法NSWOA求解微电网多目标优化…...
的几种方法)
网络爬虫|Selenium——find_element_by_xpath()的几种方法
Xpath (XML Path Language),是W3C定义的用来在XML文档中选择节点的语言 一、从根目录/开始 有点像Linux的文件查看,/代表根目录,一级一级的查找,直接子节点,相当于css_selector中的>号 /html/body/div/p 二、根据…...

【Kingbase FlySync】命令模式:部署双轨并行,并实现切换同步
【Kingbase FlySync】命令模式:安装部署同步软件,实现Oracle到KES实现同步 双轨并行方案说明一.准备工作二.环境说明三.目标实操(1).准备安装环境Orcle服务器(Oracle40)1.上传所有工具包2.操作系统配置a.增加flysync 用户、设置密码b.配置环境变量c.调整limits.conf…...

echarts 多toolti同时触发图表实现
需求背景解决效果ISQQW代码地址energyChart.vue 需求背景 需要实现同x轴,4个图表的的多图表联动效果,且滑动会触发各个图表的tooltip,即一个图表拥有4个tooltip(目前echarts不支持,我这里绕过了这个问题) 解决效果 ISQQW代码地…...
2023.11.22使用flask做一个简单的图片浏览器
2023.11.22使用flask做一个简单的图片浏览器 功能: 实现图片浏览(翻页)功能 程序页面: 程序架构: 注意:在flask中常会使用src“{{ url_for(‘static’, filename‘images/’ image) }}”,…...
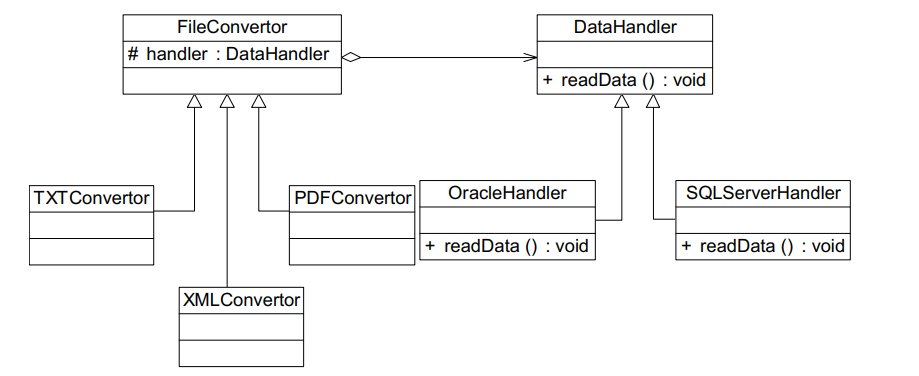
万字解析设计模式之桥接模式、外观模式
一、桥接模式 1.1概述 桥接模式是一种结构型设计模式,它的作用是将抽象部分和实现部分分离开来,使它们能够独立地变化。这样,抽象部分和实现部分可以分别进行扩展,而不会相互影响。它是用组合关系代替继承关系来实现,…...

常用系统函数
$clog2 clogb2 系统函数 $clog2 应返回参数以 2 为底的对数的上限(对数四舍五入为整数值)。参数可以是整数或任意大小的向量值。参数应被视为无符号值,参数值为 0 将产生结果 0。 该系统函数可用于计算对给定大小的存储器进行寻址所…...
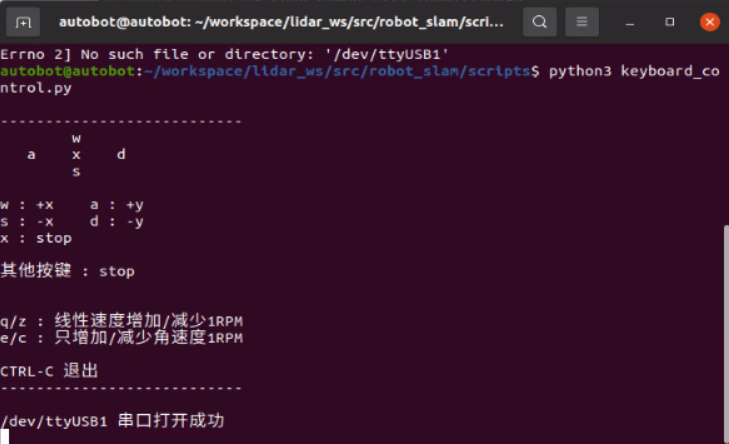
键盘控制ROS车运动
键盘控制ROS车运动 上位机 使用pyseria库与stm32单片机进行通信控制 #!/usr/bin/env python # -*- coding: utf-8 -*import sys, select, termios, tty import serialmsg """ ---------------------------w a x ds w : x a : y s : -x …...

linux上交叉编译qt库
linux上交叉编译qt库 Qt程序从X86平台Linux移植到ARM平台Linux需要做什么 1.在ubuntu上使用qt的源码交叉编译出Qt库 2.将编译好的库拷贝到开发板上并设置相应的环境变量(库路径啥的) 前两步一劳永逸,做一次就行 3.X86上写好程序代码&…...
Nacos介绍与使用
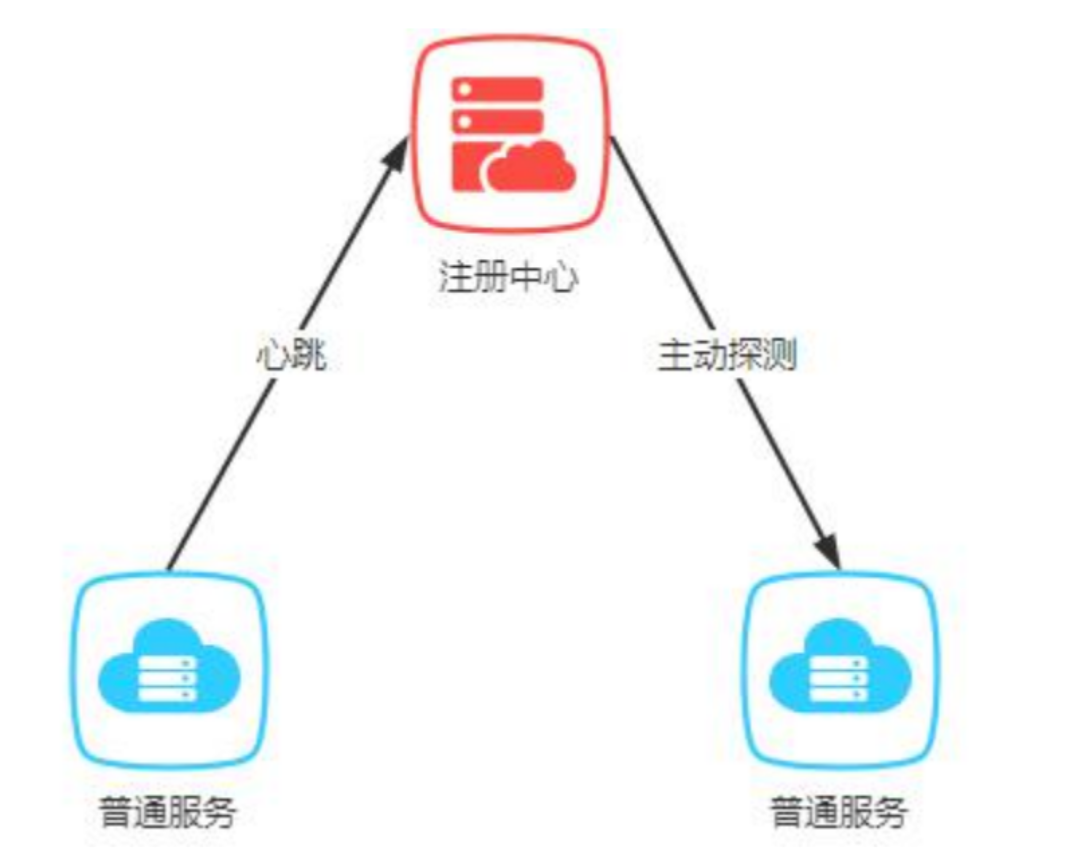
Nacos介绍与使用 文章目录 Nacos介绍与使用一. 什么是Nacos1 Nacos功能1.1 配置中心1.2 注册中心 2.为什么要使用Nacos 二.Nacos 部署安装1. Nacos 部署方式2. Nacos 安装3. 配置数据源4. 开启控制台授权登录(可选) 三. Nacos配置中心的使用1. 创建配置信…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...