# 学习 Prolog 和 离散逻辑的16个等价公式:一趟有趣的逻辑之旅

Prolog 的语法很奇怪,需要一些时间来适应,所以我花了点时间,想用Prolot来学习和验证离散逻辑的16组等价公式。
1. 双重否定律 (Double Negation Law)
A ⇔¬¬A
首先,我们来看看双重否定律。在 Prolog 中,我们可以这样验证它:
fun1(A,Z):-member(A,[false,true]),(((Z1 = not(A),Z2=not(Z1)) , equal(A,Z2)) ->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.
这个函数检查一个值和它的双重否定是否相等。是不是感觉就像在镜子里看镜子?
2. 幂等律 (Idempotent Laws)
A ⇔ A∨A
A ⇔ A∧A
接下来是幂等律,这听起来像是一种超级能力,但实际上它很简单:
fun2_1(A,Z):-member(A,[false,true]),(((Z1=(A;A)),equal(A,Z1))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun2_2(A,Z):-member(A,[false,true]),(((Z1=(A,A)),equal(A,Z1))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.
就像说“给我再多的杨幂,不如只给我一个杨幂就够了"。
3. 交换律 (Commutative Laws)
A∨B ⇔ B∨A
A∧B ⇔ B∧A
交换律告诉我们,顺序不重要,就像在决定先穿袜子还是裤子一样:
fun3_1(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=(A;B),Z2=(B;A),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.fun3_2(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=(A,B),Z2=(B,A),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
4. 结合律 (Associative Laws)
(A∨B)∨C ⇔ (A∨(B∨C)
(A∧B)∧C ⇔ (A∧(B∧C)
结合律就像是一位擅长变魔术的艺术家。就像是在告诉我们:“不管你怎么组合这些逻辑片段,结果都像是经过了魔术师的手,神奇地保持不变!”
fun4_1(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=((A;B);C),Z2=((A;(B;C)),equal(Z1,Z2)))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.fun4_2(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=((A,B),C),Z2=((A,(B,C)),equal(Z1,Z2)))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
5. 分配律 (Distributive Laws)
A∨(B∧C) ⇔ (A∨B)∧(A∨C)
A∧(B∨C) ⇔ (A∧B)∨(A∧C)
分配律像是在进行一场精彩的逻辑舞蹈。它轻松地在不同逻辑结构之间跳跃
fun5_1(A,B,C,Z):-member(A,[false,true]),member(B,[false,true]),member(C,[false,true]),(((Z1=(A;(B,C))),(Z2=((A;B),(A;C))),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w , C = ~w , Z = ~w~n',[A,B,C,Z]),fail.fun5_2(A,B,C,Z):-member(A,[false,true]),member(B,[false,true]),member(C,[false,true]),(((Z1=(A,(B;C))),(Z2=((A,B);(A,C))),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w , C = ~w , Z = ~w~n',[A,B,C,Z]),fail.
6. 德摩根律 (De Morgan Laws)
¬(A∨B) ⇔ ¬A∧¬B
¬(A∧B) ⇔ ¬A∨¬B
德摩根律就像是逻辑世界的一面镜子。当你通过这面镜子看逻辑表达式时,一切都被反转了,但令人惊奇的是,结果依然成立!
fun6_1(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Y1=(A;B),Z1=(\+Y1),Z2=(\+A,\+B),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
fun6_2(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Y1=(A,B),Z1=(\+Y1),Z2=(\+A;\+B),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
7. 吸收根律 (Absorption Laws)
A∨(A∧B) ⇔ A
A∧(A∨B) ⇔ A
吸收根律就像是一个厨师,能将一桌丰盛的菜肴减少到最基本的几样,但味道依然美妙
fun8_1(A,Z):-member(A,[false,true]),(((Z1=(A;true)),equal(Z1,true))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun8_2(A,Z):-member(A,[false,true]),(((Z1=(A,false)),equal(Z1,false))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.
8. 9. 零律和同一律 (Domination Laws & Identity Laws)
A∧1 ⇔ A
A∨0 ⇔ A
零律和同一律就像则是Prolog中的基本常量,它们是逻辑世界中的稳定点,始终如一
fun8_1(A,Z):-member(A,[false,true]),(((Z1=(A;true)),equal(Z1,true))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun8_2(A,Z):-member(A,[false,true]),(((Z1=(A,false)),equal(Z1,false))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun9_1(A,Z):-member(A,[false,true]),(((Z1=(A,true)),equal(Z1,A))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun9_1(A,Z):-member(A,[false,true]),(((Z1=(A,true)),equal(Z1,A))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun9_2(A,Z):-member(A,[false,true]),(((Z1=(A;false)),equal(Z1,false))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.
10. 11. 排中律与矛盾律 (Law of the Excluded Middle Laws & Law of Contradiction )
A∨¬A ⇔ 1
A∧¬A ⇔ 0
排中律与矛盾律这两个法则展示了逻辑的极端情况,一方面是充分性,另一方面是不可能性。
fun10(A,Z):-member(A,[false,true]),(((Z1=(A;\+A)),equal(Z1,true))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.fun11(A,Z):-member(A,[false,true]),(((Z1=(A,\+A)),equal(Z1,false))->Z=true;Z=false),format('A = ~w , Z = ~w~n',[A,Z]),fail.
12. 13. 蕴涵律和等价律 (Implication Laws & Eqivalence Laws)
A→B ⇔ ¬A∨B
A↔B ⇔ (A→B )∧(B→A)
蕴涵律和等价律是理解逻辑关系的核心
fun12(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=(A->B;true),Z2=(\+A;B),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.fun13(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=equal(A,B),Z2=(contain(A,B),contain(B,A)),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
14. 15. 假言易位律与等价否定律 (Contraposition Laws and Negation of Equivalence Laws)
A→B ⇔ ¬B→¬A
A↔B ⇔ ¬A↔¬B
假言易位律与等价否定律展示了逻辑表达式的巧妙转换,就像是逻辑世界的变形术,展示了多种面貌
fun14(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=contain(A,B),Y1=(\+B),Y2=(\+A),Z2=(contain(Y1,Y2)),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.fun15(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Z1=equal(A,B),Y1=(\+A),Y2=(\+B),Z2=(equal(Y1,Y2)),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.
16. 归谬律 (Reductio ad Absurdum)
(A→B) ∧(A→¬B) ⇔ ¬A
归谬律是Prolog中逻辑推理的终极检验,它揭示了逻辑中的悖论和矛盾
fun16(A,B,Z):-member(A,[false,true]),member(B,[false,true]),((Y1=(\+B),Z1=(contain(A,B),contain(A,Y1)),Z2=(\+A),equal(Z1,Z2))->Z=true;Z=false),format('A = ~w , B = ~w, Z = ~w~n',[A,B,Z]),fail.相关文章:

# 学习 Prolog 和 离散逻辑的16个等价公式:一趟有趣的逻辑之旅
Prolog 的语法很奇怪,需要一些时间来适应,所以我花了点时间,想用Prolot来学习和验证离散逻辑的16组等价公式。 1. 双重否定律 (Double Negation Law) A ⇔A 首先,我们来看看双重否定律。在 Prolog 中,我们可以这样验证它: fun1(A,Z):-memb…...
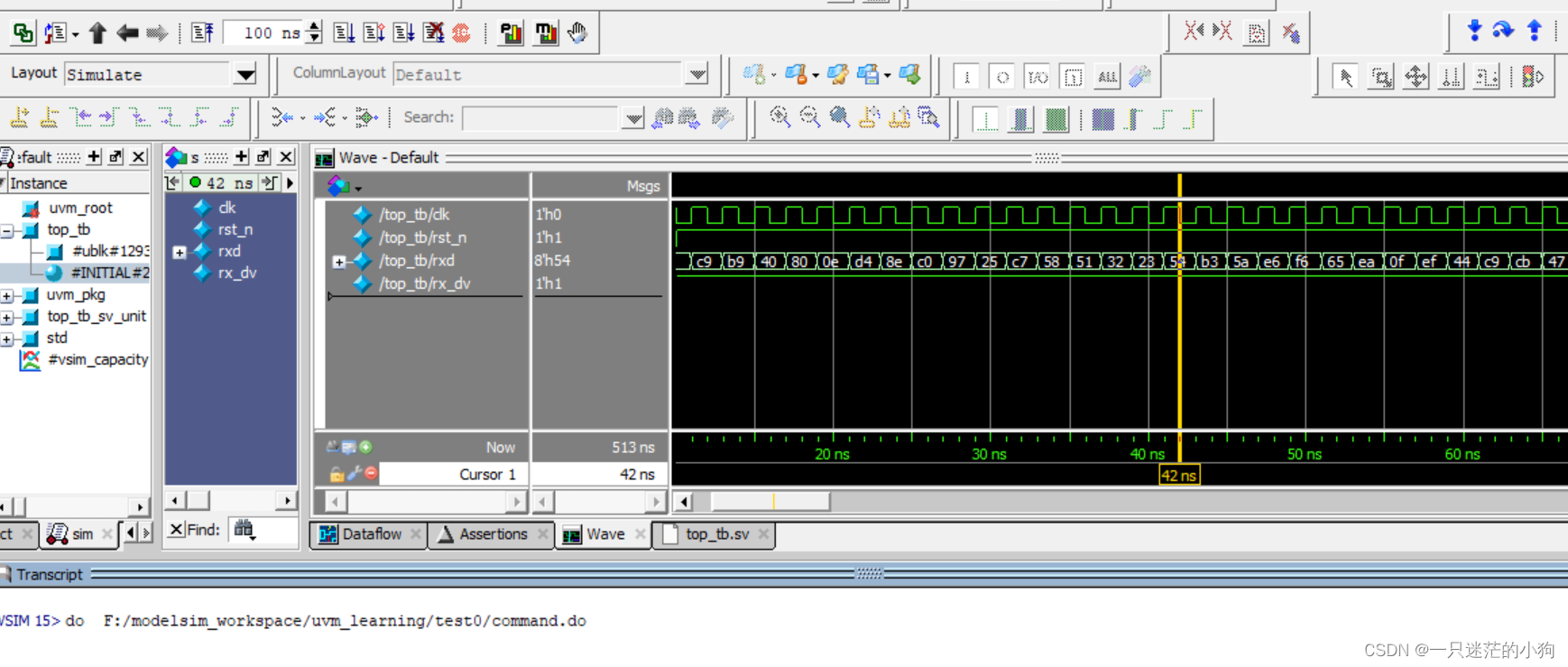
Win11+Modelsim SE-64 10.6d搭建UVM环境
1、添加源文件及tb文件 在目录下建立文件夹,将DUT和Testbench添加进去,文件夹内容如下所示: 2、以《UVM实战》中的例子做简单的示例: 2.1 设计文件 :dut.sv 功能很简单,即将接受到的数据原封不动发送出去…...
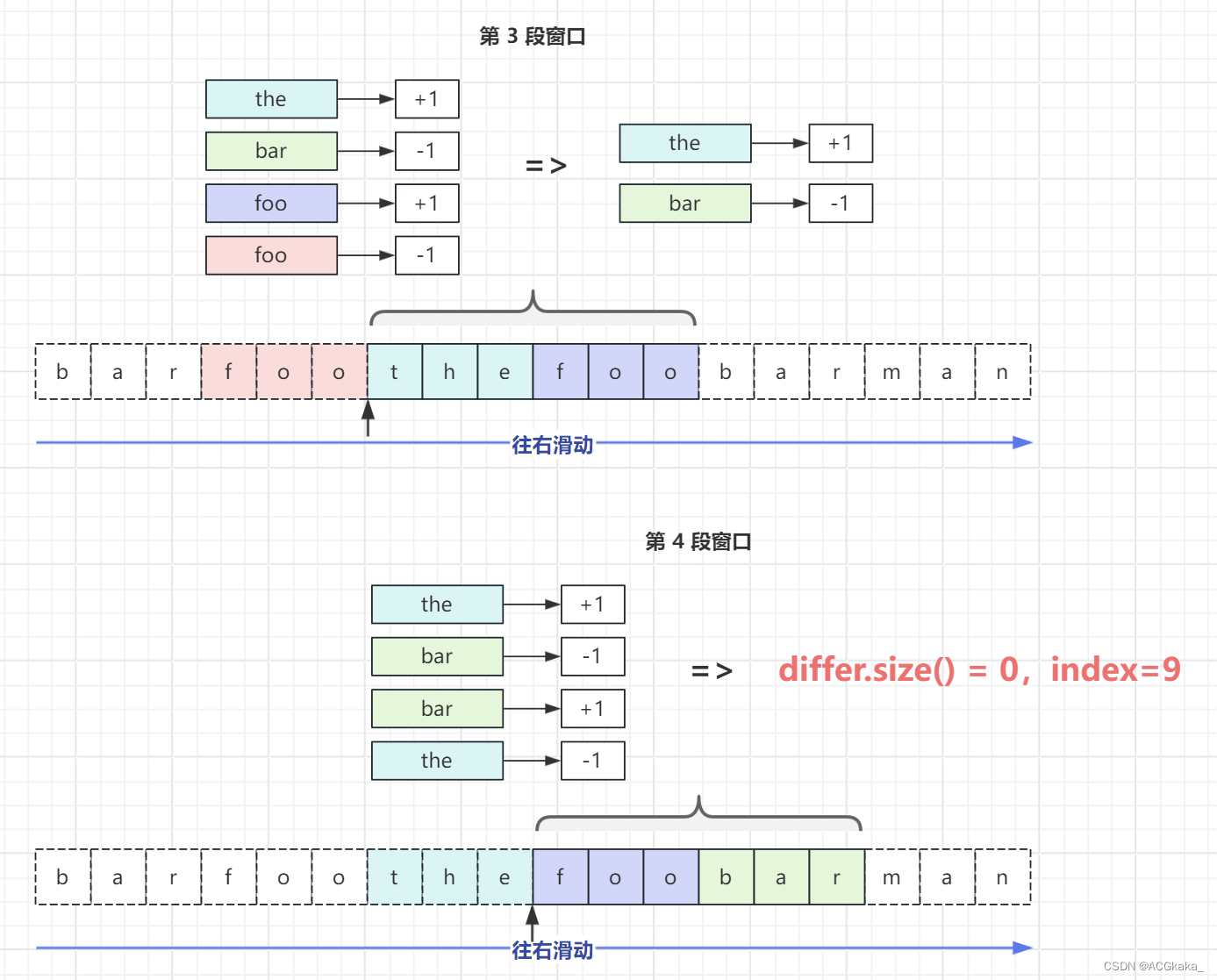
LeetCode(32)串联所有单词的子串【滑动窗口】【困难】(含图解)
目录 1.题目2.答案3.提交结果截图4.图解 链接: 串联所有单词的子串 1.题目 给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。 s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。 例如,如果 w…...
【Delphi】使用TWebBrowser执行JavaScript命令传入JSON参数执行出错解决方案
目录 一、问题背景: 二、实际示例: 三、解决方案: 1. Delphi 代码: 2. javaScript代码: 一、问题背景: 在用Delphi开发程序,无论是移动端还是PC端,都可以很方便的使用TWebBrows…...

04 if进阶
elif 否则如果 如果条件没有满足 会继续进入“否则如果”里面判断 只要满足一个条件 条件判断立即终止 chinese 100 if chinese 100:print("我们去迪士尼玩")elif chinese > 90:print("我们去朱雀森林公园")else:print("回家写作业")if n…...

2023全球数字贸易创新大赛9-12
目录 回答评委提问:先说痛点-再说怎样解决 食品安全溯源是否全流程 星火• 链网...
vue3的两个提示[Vue warn]: 关于组件渲染和函数外部使用
1. [Vue warn]: inject() can only be used inside setup() or functional components. 这个消息是提示我们,需要将引入的方法作为一个变量使用。以vue-store为例,如果我们按照如下的方式使用: import UseUserStore from ../../store/module…...

Ubuntu环境下基于libxl库文件使用C++实现对表格的操作
功能 表格不存在则创建后再进行操作创建sheet添加新的工作表在sheet中增加数据设置单元格样式 相关配置 下载地址:libxl选择 LibXL for Linux 4.2.0 i386 x64 armhf aarch64 安装配置 1,使用 tar zxvf 文件名.tar.gz 进行文件解压2,创…...

Sentinel与SpringBoot整合
好的,以下是一个简单的Spring Cloud整合Sentinel的代码示例: 首先,在pom.xml中添加以下依赖: <dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-sentinel&l…...

如何实现数据通过表格批量导入数据库
文章目录 1. 准备工作2. 创建数据库表3. 编写导入脚本4. 优化和拓展4.1 批量插入的优势4.2 错误处理4.3 数据验证4.4 数据转换 5. 总结 🎉如何实现数据通过表格批量导入数据库 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客&…...
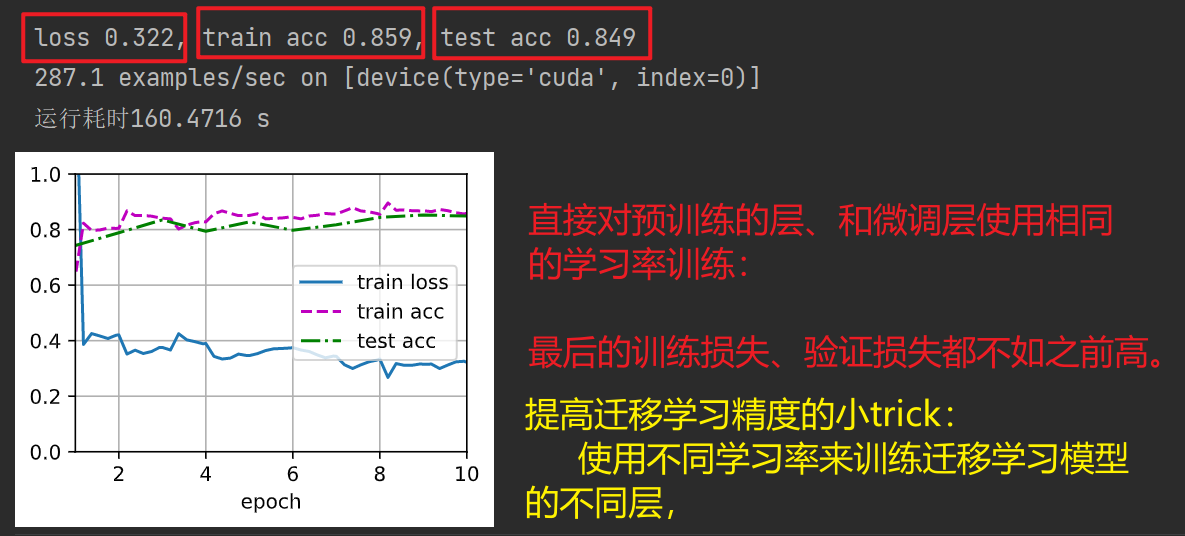
(动手学习深度学习)第13章 计算机视觉---微调
文章目录 微调总结 微调代码实现 微调 总结 微调通过使用在大数据上的恶道的预训练好的模型来初始化模型权重来完成提升精度。预训练模型质量很重要微调通常速度更快、精确度更高 微调代码实现 导入相关库 %matplotlib inline import os import torch import torchvision f…...
,剑指offer,力扣)
训练跳跃(青蛙跳台阶),剑指offer,力扣
目录 题目地址: 题目: 青蛙跳台阶问题 我们直接看题解吧: 相似题目,斐波那契数列: 解题方法: 难度分析: 审题目事例提示: 解题思路: 代码实现: 小鸡识补充 题…...

Linux中路由route
route 显示当前路由表信息 route add -net 192.168.10.0 netmask 255.255.255.0 dev ens160去往192.168.10.0/24网段的路由通过ens160网卡出去add 添加路由(del表示删除路由)-A 设置地址类型(默认ipv4 配置ipv6地址时:-A …...

美国国家安全实验室员工详细数据在网上泄露
一个从事出于政治动机的攻击的网络犯罪组织破坏了爱达荷国家实验室(INL)的人力资源应用程序,该组织周日在电报上发帖称,已获得该核研究实验室员工的详细信息。 黑客组织 SiegedSec 表示,它已经访问了“数十万用户、员…...

一石激起千层浪,有关奥特曼被炒的消息引发了一场热烈的讨论
在毫无征兆的情况下,OpenAI CEO山姆-奥特曼被炒了。 一石激起千层浪,有关奥特曼被炒的消息引发了一场热烈的讨论。 有人将其看成是一场「宫斗」,有人将其看成是OpenAI的董事会与创始人们的一次纠偏。 无论如何,这样一件看似并无…...
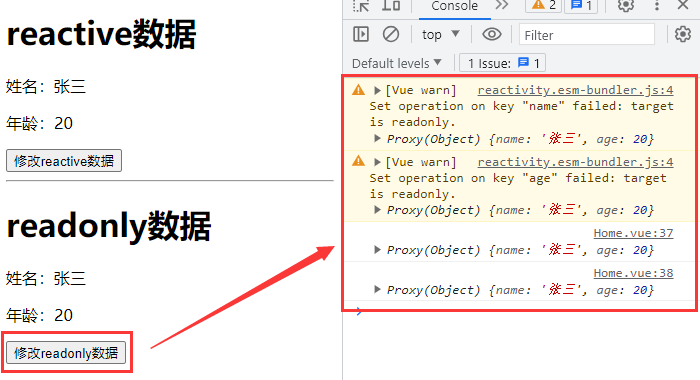
Vue 定义只读数据 readonly
readonly 让一个响应式数据变为 **深层次的只读数据**。 isReadonly 判断一个数据是不是只读数据。 应用场景:不希望数据被修改时使用。 readonly 深层次只读: <template><h1>reactive数据</h1><p>姓名:{{ info…...

[Linux] Network: IPv6 link-local 地址是否可用不自动生成
原来有一段时间在做扩充产品的VLAN个数,然后就遇到过一个问题:说这个Linux的默认配置里,会为每一个网络接口添加一个link-local的地址,就是FE80::开头的地址,在RFC-4291里有如下的定义: Link-Local unicas…...

万字解析:十大排序(直接插入排序+希尔排序+选择排序+堆排序+冒泡排序+快速排序+归并排序+计数排序+基数排序+桶排序)
文章目录 十大排序排序算法复杂度及稳定性分析一、 排序的概念1.排序:2.稳定性:3.内部排序:4.外部排序: 二、插入排序1.直接插入排序2.希尔排序 三、选择排序1.直接选择排序方法一方法二直接插入排序和直接排序的区别 2.堆排序 四…...

基于原子轨道搜索算法优化概率神经网络PNN的分类预测 - 附代码
基于原子轨道搜索算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于原子轨道搜索算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于原子轨道搜索优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要…...

“我,24岁,年薪20万”:选对了行业究竟多重要?
那些在职场上顺风顺水,按部就班拿到高薪的人都有什么特点? 今天的主人公Flee告诉我,是稳。 在她的故事里,我看到一个“别人家的姑娘”,是怎样在职场上稳步晋升,大学毕业仅2年,就拿到18.6K月薪&a…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
