AcWing算法提高课-3.1.1热浪
宣传一下算法提高课整理 <—
CSDN个人主页:更好的阅读体验 <—

题目传送门点这里
题目描述
德克萨斯纯朴的民众们这个夏天正在遭受巨大的热浪!!!
他们的德克萨斯长角牛吃起来不错,可是它们并不是很擅长生产富含奶油的乳制品。
农夫John此时身先士卒地承担起向德克萨斯运送大量的营养冰凉的牛奶的重任,以减轻德克萨斯人忍受酷暑的痛苦。
John已经研究过可以把牛奶从威斯康星运送到德克萨斯州的路线。
这些路线包括起始点和终点一共有 T 个城镇,为了方便标号为 1 到 T。
除了起点和终点外的每个城镇都由 双向道路 连向至少两个其它的城镇。
每条道路有一个通过费用(包括油费,过路费等等)。
给定一个地图,包含 C 条直接连接 2 个城镇的道路。
每条道路由道路的起点 Rs,终点 Re 和花费 Ci 组成。
求从起始的城镇 Ts 到终点的城镇 Te 最小的总费用。
输入格式
第一行: 444 个由空格隔开的整数: T,C,Ts,TeT,C,T_s,T_eT,C,Ts,Te;
第 222 到第 C+1C+1C+1 行: 第 i+1i+1i+1 行描述第 iii 条道路,包含 333 个由空格隔开的整数: Rs,Re,CiR_s,R_e,C_iRs,Re,Ci。
输出格式
一个单独的整数表示从 TsT_sTs 到 TeT_eTe 的最小总费用。
数据保证至少存在一条道路。
数据范围
1≤T≤2500,1≤T≤2500,1≤T≤2500,
1≤C≤6200,1≤C≤6200,1≤C≤6200,
1≤Ts,Te,Rs,Re≤T,1≤T_s,T_e,R_s,R_e≤T,1≤Ts,Te,Rs,Re≤T,
1≤Ci≤10001≤C_i≤10001≤Ci≤1000
样例输入
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
样例输出
7
思路
我们先抽象出图:
题目的大致意思是,给定一个无向图并给定起点和终点,求其最短路径。
这就基本上是一道模板题了,作者在这里是用朴素Dijkstra算法写的。当然,有些同学为了节省时间,可能会用SPFA。但,这是个正权图,如果出题人非常敬业 (邪恶) 的话,就会把SPFA卡掉。
所以在OI赛制下,正权图的最短路尽量还是用Dijkstra,除非时间限制真的不够用。
因为本题的点数和边数都不是很大,所以原则上,无论用邻接表或者邻接矩阵都是可以存下的。
算法时间复杂度
假定这里n表示点数,m表示边数,则:
朴素Dijkstra算法的时间复杂度是O(n2)O(n^2)O(n2);
SPFA算法的时间复杂度一般是O(m)O(m)O(m),最坏情况下是O(nm)O(nm)O(nm);
堆优化Dijkstra的时间复杂度是O(mlogn)O(m \log n)O(mlogn)
AC Code
C++C++C++
#include <iostream>
#include <cstring>using namespace std;const int N = 2520;int n, m, st, ed;
int g[N][N]; // 邻接矩阵存图
int dist[N]; // 存最短距离
bool f[N]; // 找过的点的集合int dijkstra(int st, int ed) // Dijkstra算法
{memset(dist, 0x3f, sizeof(dist)); // 初始化dist数组dist[st] = 0; // 起点距离设置为0for (int i = 1; i <= n; i ++ ){int t = -1;for (int j = 1; j <= n; j ++ )if (!f[j] && (t == -1 || dist[j] < dist[t]))t = j; // 找到当前与源点距离最短的那个点f[t] = 1; // 将该点标记上,表示这个点已经找过了for (int j = 1; j <= n; j ++ )dist[j] = min(dist[j], dist[t] + g[t][j]); // 用这个点更新源点与其他点的最短距离}return dist[ed]; // 返回st->ed的最短距离
}int main()
{memset(g, 0x3f, sizeof(g)); // 初始化邻接矩阵int a, b, c;scanf("%d%d", &n, &m);scanf("%d%d", &st, &ed);while (m -- ){scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c);g[b][a] = min(g[b][a], c); // 因为可能有重边,所以需要取最小值}int res = dijkstra(st, ed);printf("%d\n", res); // 数据保证有解,故不需要判断return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-3.1.1热浪
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 德克萨斯纯朴的民众们这个夏天正在遭受巨大的热浪!!! 他们的德克萨斯长角牛吃起来不错,可是它们并不是很擅长生产富…...

华为OD机试题【最差产品奖】用 C++ 编码,速通 (2023.Q1)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明最差产…...

NFT市场大战:Blur市场地位可持续吗?
在战胜无数虚张声势的挑战者之后,OpenSea终于迎来了一个实力雄厚的竞争对手,已威胁到它的市场主导地位。opensea是什么?参考《NFT,区块链的产物之一,了解NFT交易平台Opensea》 继成功的空投之后,Blur并没有…...

初识CSS
1.CSS语法形式CSS基本语法规则就是:选择器若干属性声明由选择器选择一个元素,其中的属性声明就作用于该元素.比如:<body><p>这是一个段落</p><!-- style可以放在代码的任意地方 --><style>p{/* 将字体颜色设置为红色 */color: red;}</style&g…...
知识总结(第3期))
kubernetes(k8s)知识总结(第3期)
1. PV 与 PVC PV 是持久卷(Persistent Volume)的首字母缩写。通常情况下,可以事先在 k8s 集群创建 PV 对象: apiVersion: v1 kind: PersistentVolume metadata:name: nfs spec:storageClassName: manualcapacity:storage: 1Giac…...

浅谈跨境电商运行模式
近些年,由于疫情的原因和人们的消费习惯的改变,线下销售越来越不占优势,电商行业由于这几年的飞速发展,成功地吸引到我国的民众,拼多多、淘宝、京东、天猫等各种各样的国内电商平台涌现,依靠着产品质量好、…...

Memcached
什么是MemcachedMemcached 是一个开源免费的高性能的分布式内存对象缓存系统、就是一个软件Memcached的作用缓存数据提高动态网站的速度Memcached的安装//方法一yum installmemcached//方法二1.安装libevent (memcached依赖包)tar -zvxflibevent-release-1.4.15-stable.tar.gzc…...
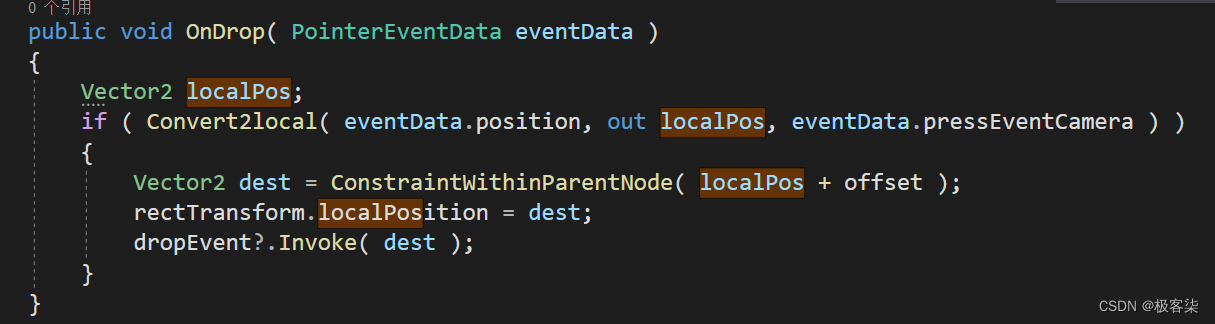
Unity UGUI 拖拽组件
效果展示 使用方式 拖到图片上即可用 父节点会约束它的活动范围哦~ 父节点会约束它的活动范围哦~ 父节点会约束它的活动范围哦~ 源码 using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.EventSystems;/// <summary> /…...

面试总结——react生命周期
react生命周期总结 生命周期主要分为以下几个阶段: Mounting:创建虚拟DOM,渲染UI(初始化)Updating:更新虚拟DOM,重新渲染UI;(更新)UnMounting:删除虚拟DOM,移除UI;(销毁) 生命周期…...

初探推荐系统-01
文章目录一、什么是推荐系统是什么为什么长尾理论怎么做二、相似度算法杰卡德相似系数余弦相似度三、基于内容的推荐算法如何获取到用户喜欢的物品如何确定物品的特征四、推荐算法实验方法评测指标推荐效果实验方法1、离线实验2、用户调查3、在线实验评测指标1、预测准确度评分…...

html实现浪漫的爱情日记(附源码)
文章目录1.设计来源1.1 主界面1.2 遇见1.3 相熟1.4 相知1.5 相念2.效果和源码2.1 动态效果2.2 源代码2.3 代码结构源码下载更多爱情表白源码作者:xcLeigh 文章地址:https://blog.csdn.net/weixin_43151418/article/details/129264757 html实现浪漫的爱情…...
)
detectron2容器环境安装问题(1)
1为避免后面出现需求python版本低于3.7的情况ERROR: Package detectron2 requires a different Python: 3.6.9 not in >3.7可以第一步就使用 nvidia/cuda:11.1.1-cudnn8-devel-ubuntu20.04镜像2如果使用了18.04的镜像nvidia/cuda:11.1.1-cudnn8-devel-ubuntu18.04可以使用我…...
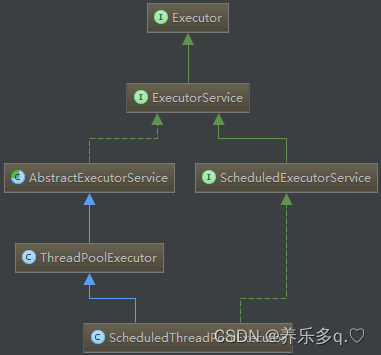
JAVA线程池原理详解二
JAVA线程池原理详解二 一. Executor框架 Eexecutor作为灵活且强大的异步执行框架,其支持多种不同类型的任务执行策略,提供了一种标准的方法将任务的提交过程和执行过程解耦开发,基于生产者-消费者模式,其提交任务的线程相当于生…...

Java 常用 API
文章目录一、Math二、System三、Object1. toString() 方法2. equals() 方法四、Arrays1. 冒泡排序2. Arrays 常用方法五、基本类型包装类1. Integer2. int 和 String 相互转换3. 字符串中数据排序4. 自动装箱和拆箱六、日期类1. Date2. SimpleDateFormat3. Calendar4. 二月天一…...

记一次分布式环境下TOKEN实现用户登录
背景: 以前的单体项目,使用的是session来保存用户登录状态,控制用户的登录过期时间等信息,但是这个session是只保存在该服务器的这个系统内存中。系统只有一个服务就没关系,但是如果是分布式的服务,每个…...

用cpolar发布本地的论坛网站 1
网页论坛向来是个很神奇的地方,曾经的天涯论坛和各种BBS,大家聚在在一起讨论某个问题,也能通过论坛发布想法,各种思维碰撞在一起,发生很多有趣的故事,也产生了很多流传一时的流行语录。当然,如果…...

CSS的4种引入方式
CSS的4种引入方式 目录CSS的4种引入方式一、内嵌式:CSS写在style标签中二、外联式:CSS写在一个单独的.css文件中三、行内式:CSS写在标签的style属性中四、导入外部样式五、css引用的优先级六、link和import的区别一、内嵌式:CSS写…...
Shell高级——Linux中的文件描述符(本质是数组的下标)
以下内容源于C语言中文网的学习与整理,非原创,如有侵权请告知删除。 前言 Linux中一切接文件,比如 C 源文件、视频文件、Shell脚本、可执行文件等,就连键盘、显示器、鼠标等硬件设备也都是文件。 一个 Linux 进程可以打开成百上…...
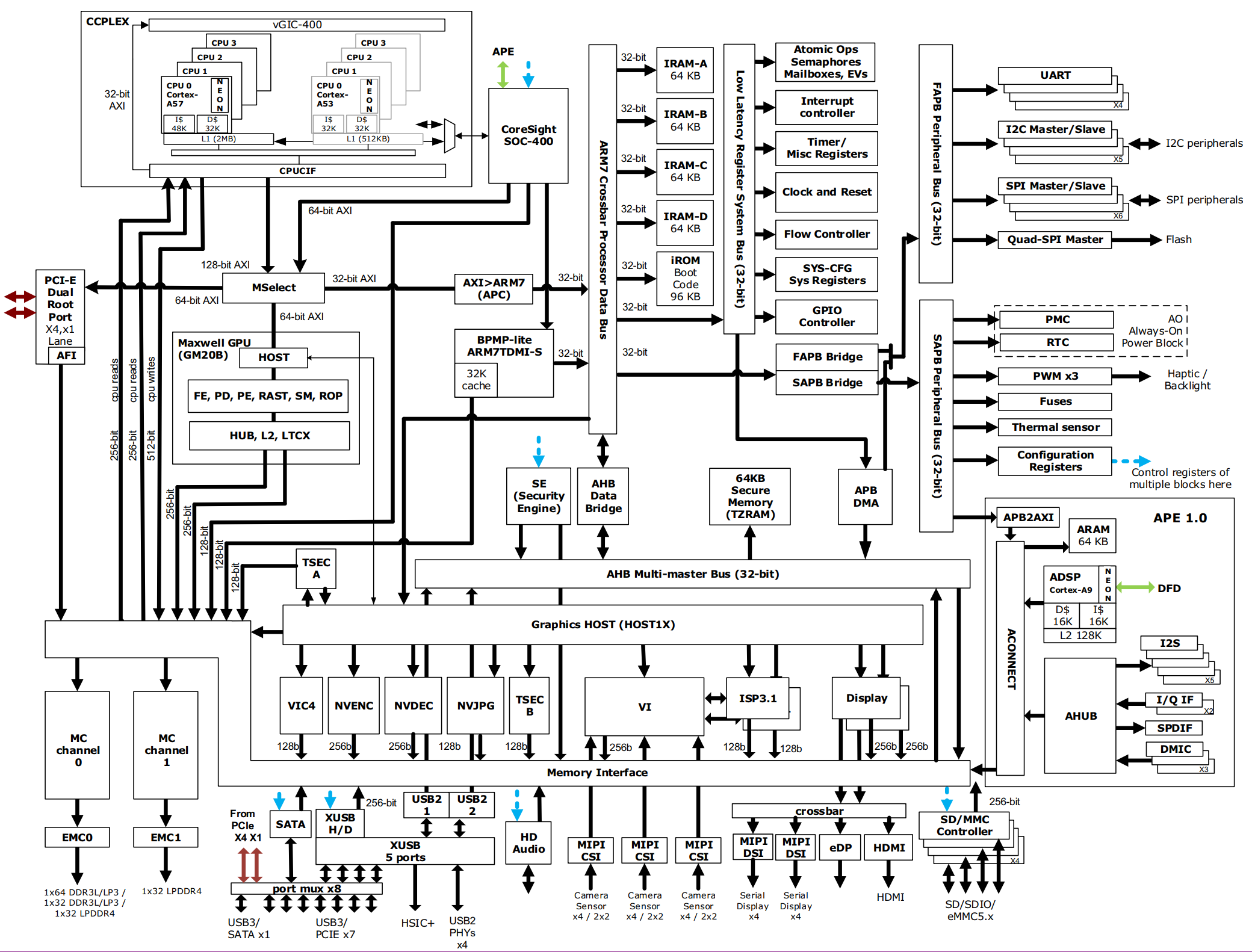
Nvidia jetson nano硬件架构
资料来源 官方文档中心 https://developer.nvidia.com/embedded/downloads -> 选jetson -> Jetson Nano Product Design Guide //产品设计指导(入口) //-> 1.1 References 列出了相关的文档 -> Jetson Nano Developer Kit Carrier Board Specification //板子标注…...

ffmpeg多路同时推流
一、ffmpeg常见使用方法1.1利用FFMPEG命令进行文件分割1.2转换格式1.3推流配置方法一:ngnix(不推荐,推流不好使)方法二:srs(强烈推荐)1.4查看nginx启动是否成功二、ffmpeg推流——>ngnix单路…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
