python数据结构与算法-15_堆与堆排序
堆(heap)
前面我们讲了两种使用分治和递归解决排序问题的归并排序和快速排序,中间又穿插了一把树和二叉树,
本章我们开始介绍另一种有用的数据结构堆(heap), 以及借助堆来实现的堆排序,相比前两种排序算法要稍难实现一些。
最后我们简单提一下 python 标准库内置的 heapq 模块。
什么是堆?
堆是一种完全二叉树(请你回顾下上一章的概念),有最大堆和最小堆两种。
- 最大堆: 对于每个非叶子节点 V,V 的值都比它的两个孩子大,称为 最大堆特性(heap order property)
最大堆里的根总是存储最大值,最小的值存储在叶节点。 - 最小堆:和最大堆相反,每个非叶子节点 V,V 的两个孩子的值都比它大。

堆的操作
堆提供了很有限的几个操作:
- 插入新的值。插入比较麻烦的就是需要维持堆的特性。需要 sift-up 操作,具体会在视频和代码里解释,文字描述起来比较麻烦。
- 获取并移除根节点的值。每次我们都可以获取最大值或者最小值。这个时候需要把底层最右边的节点值替换到 root 节点之后
执行 sift-down 操作。


堆的表示
上一章我们用一个节点类和二叉树类表示树,这里其实用数组就能实现堆。

仔细观察下,因为完全二叉树的特性,树不会有间隙。对于数组里的一个下标 i,我们可以得到它的父亲和孩子的节点对应的下标:
parent = int((i-1) / 2) # 取整
left = 2 * i + 1
right = 2 * i + 2
超出下标表示没有对应的孩子节点。
实现一个最大堆
我们将在视频里详细描述和编写各个操作
class MaxHeap(object):def __init__(self, maxsize=None):self.maxsize = maxsizeself._elements = Array(maxsize)self._count = 0def __len__(self):return self._countdef add(self, value):if self._count >= self.maxsize:raise Exception('full')self._elements[self._count] = valueself._count += 1self._siftup(self._count-1) # 维持堆的特性def _siftup(self, ndx):if ndx > 0:parent = int((ndx-1)/2)if self._elements[ndx] > self._elements[parent]: # 如果插入的值大于 parent,一直交换self._elements[ndx], self._elements[parent] = self._elements[parent], self._elements[ndx]self._siftup(parent) # 递归def extract(self):if self._count <= 0:raise Exception('empty')value = self._elements[0] # 保存 root 值self._count -= 1self._elements[0] = self._elements[self._count] # 最右下的节点放到root后siftDownself._siftdown(0) # 维持堆特性return valuedef _siftdown(self, ndx):left = 2 * ndx + 1right = 2 * ndx + 2# determine which node contains the larger valuelargest = ndxif (left < self._count and # 有左孩子self._elements[left] >= self._elements[largest] andself._elements[left] >= self._elements[right]): # 原书这个地方没写实际上找的未必是largestlargest = leftelif right < self._count and self._elements[right] >= self._elements[largest]:largest = rightif largest != ndx:self._elements[ndx], self._elements[largest] = self._elements[largest], self._elements[ndx]self._siftdown(largest)def test_maxheap():import randomn = 5h = MaxHeap(n)for i in range(n):h.add(i)for i in reversed(range(n)):assert i == h.extract()
实现堆排序
上边我们实现了最大堆,每次我们都能 extract 一个最大的元素了,于是一个倒序排序函数就能很容易写出来了:
def heapsort_reverse(array):length = len(array)maxheap = MaxHeap(length)for i in array:maxheap.add(i)res = []for i in range(length):res.append(maxheap.extract())return resdef test_heapsort_reverse():import randoml = list(range(10))random.shuffle(l)assert heapsort_reverse(l) == sorted(l, reverse=True)
Python 里的 heapq 模块
python 其实自带了 heapq 模块,用来实现堆的相关操作,原理是类似的。请你阅读相关文档并使用内置的 heapq 模块完成堆排序。
一般我们刷题或者写业务代码的时候,使用这个内置的 heapq 模块就够用了,内置的实现了是最小堆。
Top K 问题
面试题中有这样一类问题,让求出大量数据中的top k 个元素,比如一亿个数字中最大的100个数字。
对于这种问题有很多种解法,比如直接排序、mapreduce、trie 树、分治法等,当然如果内存够用直接排序是最简单的。
如果内存不够用呢? 这里我们提一下使用固定大小的堆来解决这个问题的方式。
一开始的思路可能是,既然求最大的 k 个数,是不是应该维护一个包含 k 个元素的最大堆呢?
稍微尝试下你会发现走不通。我们先用数组的前面 k 个元素建立最大堆,然后对剩下的元素进行比对,但是最大堆只能每次获取堆顶
最大的一个元素,如果我们取下一个大于堆顶的值和堆顶替换,你会发现堆底部的小数一直不会被换掉。如果下一个元素小于堆顶
就替换也不对,这样可能最大的元素就被我们丢掉了。
相反我们用最小堆呢?
先迭代前 k 个元素建立一个最小堆,之后的元素如果小于堆顶最小值,跳过,否则替换堆顶元素并重新调整堆。你会发现最小堆里
慢慢就被替换成了最大的那些值,并且最后堆顶是最大的 topk 个值中的最小值。
(比如1000个数找10个,最后堆里剩余的是 [990, 991, 992, 996, 994, 993, 997, 998, 999, 995],第一个 990 最小)
按照这个思路很容易写出来代码:
import heapqclass TopK:"""获取大量元素 topk 大个元素,固定内存思路:1. 先放入元素前 k 个建立一个最小堆2. 迭代剩余元素:如果当前元素小于堆顶元素,跳过该元素(肯定不是前 k 大)否则替换堆顶元素为当前元素,并重新调整堆"""def __init__(self, iterable, k):self.minheap = []self.capacity = kself.iterable = iterabledef push(self, val):if len(self.minheap) >= self.capacity:min_val = self.minheap[0]if val < min_val: # 当然你可以直接 if val > min_val操作,这里我只是显示指出跳过这个元素passelse:heapq.heapreplace(self.minheap, val) # 返回并且pop堆顶最小值,推入新的 val 值并调整堆else:heapq.heappush(self.minheap, val) # 前面 k 个元素直接放入minheapdef get_topk(self):for val in self.iterable:self.push(val)return self.minheapdef test():import randomi = list(range(1000)) # 这里可以是一个可迭代元素,节省内存random.shuffle(i)_ = TopK(i, 10)print(_.get_topk()) # [990, 991, 992, 996, 994, 993, 997, 998, 999, 995]if __name__ == '__main__':test()
源码
# python3
class MinHeap:def __init__(self):"""这里提供一个最小堆实现。如果面试不让用内置的堆非让你自己实现的话,考虑用这个简版的最小堆实现。一般只需要实现 heqppop,heappush 两个操作就可以应付面试题了parent: (i-1)//2。注意这么写 int((n-1)/2), python3 (n-1)//2当n=0结果是-1而不是0left: 2*i+1right: 2*i+2参考:https://favtutor.com/blogs/heap-in-pythonhttps://runestone.academy/ns/books/published/pythonds/Trees/BinaryHeapImplementation.htmlhttps://www.askpython.com/python/examples/min-heap"""self.pq = []def min_heapify(self, nums, k):"""递归调用,维持最小堆特性"""l = 2*k+1 # 左节点位置r = 2*k+2 # 右节点if l < len(nums) and nums[l] < nums[k]:smallest = lelse:smallest = kif r < len(nums) and nums[r] < nums[smallest]:smallest = rif smallest != k:nums[k], nums[smallest] = nums[smallest], nums[k]self.min_heapify(nums, smallest)def heappush(self, num):"""列表最后就加入一个元素,之后不断循环调用维持堆特性"""self.pq.append(num)n = len(self.pq) - 1# 注意必须加上n>0。因为 python3 (n-1)//2 当n==0 的时候结果是-1而不是0!while n > 0 and self.pq[n] < self.pq[(n-1)//2]: # parent 交换self.pq[n], self.pq[(n-1)//2] = self.pq[(n-1)//2], self.pq[n] # swapn = (n-1)//2def heqppop(self): # 取 pq[0],之后和pq最后一个元素pq[-1]交换之后调用 min_heapify(0)minval = self.pq[0]last = self.pq[-1]self.pq[0] = lastself.min_heapify(self.pq, 0)self.pq.pop()return minvaldef heapify(self, nums):n = int((len(nums)//2)-1)for k in range(n, -1, -1):self.min_heapify(nums, k)def test_MinHeqp():import randoml = list(range(1, 9))random.shuffle(l)pq = MinHeap()for num in l:pq.heappush(num)res = []for _ in range(len(l)):res.append(pq.heqppop()) # 利用 heqppop,heqppush 实现堆排序def issorted(l): return all(l[i] <= l[i+1] for i in range(len(l) - 1))assert issorted(res)
练习题
- 这里我用最大堆实现了一个 heapsort_reverse 函数,请你实现一个正序排序的函数。似乎不止一种方式
- 请你实现一个最小堆,你需要修改那些代码呢?
- 我们实现的堆排序是 inplace 的吗,如果不是,你能改成 inplace 的吗?
- 堆排序的时间复杂度是多少? siftup 和 siftdown 的时间复杂度是多少?(小提示:考虑树的高度,它决定了操作次数)
- 请你思考 Top K 问题的时间复杂度是多少?
延伸阅读
- 《算法导论》第 6 章 Heapsort
- 《Data Structures and Algorithms in Python》 13.5 节 Heapsort
- 阅读 Python heapq 模块的文档
Leetcode
合并 k 个有序链表 https://leetcode.com/problems/merge-k-sorted-lists/description/
相关文章:

python数据结构与算法-15_堆与堆排序
堆(heap) 前面我们讲了两种使用分治和递归解决排序问题的归并排序和快速排序,中间又穿插了一把树和二叉树, 本章我们开始介绍另一种有用的数据结构堆(heap), 以及借助堆来实现的堆排序,相比前两种排序算法要稍难实现一些。 最后我…...
vscode提交代码到Gitee(保姆教程)
Visual Studio Code(VSCode) 提交代码到Gitee(保姆教程) 1 环境配置1.1 git本地安装1.2 Vscode安装1.3 配置注册gitee账号 2 Vscode代码提交到Gitee2.1 新建仓库2.2 Vscode提交代码 1 环境配置 电脑需要已经安装好的Vscode已经配…...

【洛谷算法题】P5714-肥胖问题【入门2分支结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5714-肥胖问题【入门2分支结构】🌏题目描述🌏输入格式&a…...

促进材料基因工程基础理论、前沿技术和关键装备的发展和应用,第七届材料基因工程高层论坛将于12月重庆举办,龙讯旷腾出席会议
为了进一步促进材料基因工程基础理论、前沿技术和关键装备的发展和应用,加强国际交流,加速我国新材料的研发和应用,由中国材料研究学会、西部科学城重庆高新区管理委员会主办,重庆大学、北京科技大学、北京云智材料大数据研究院等…...

Cypress-浏览器操作篇
Cypress-浏览器操作篇 页面的前进与后退 后退 cy.go(back); cy.go(-1);前进 cy.go(forward); cy.go(1);页面刷新 cy.reload() cy.reload(forceReload) cy.reload(options) cy.reload(forceReload, options)**options:**只有 timeout 和 log forceReload 是否…...
短视频矩阵系统源码搭建部署分享
一、 短视频矩阵系统源码搭建部署分享 目录 一、 短视频矩阵系统源码搭建部署分享 二、短视频矩阵系统搭建功能设计 三、 抖音矩阵号矩阵系统功能设计原则 四、 短视频矩阵开发部分源码展示 很高兴能够帮助您,以下是短视频矩阵系统源码搭建部署分享:…...

科技赋能,创新发展!英码科技受邀参加2023中国创新创业成果交易会
11月17日至19日,2023中国创新创业成果交易会(简称:创交会)在广州市广交会展馆圆满举行。英码科技受邀参加本届创交会,并在会场展示了创新性的AIoT产品、深元AI引擎和行业热门解决方案。 据介绍,本届创交会由…...

Talk | UCSB博士生宋珍巧:基于人工智能的功能性蛋白质设计
本期为TechBeat人工智能社区第549期线上Talk。 北京时间11月22日(周三)20:00,UC Santa Barbara博士生—宋珍巧的Talk已准时在TechBeat人工智能社区开播! 她与大家分享的主题是: “基于人工智能的功能性蛋白质设计”,介绍了如何利用机器学习算…...
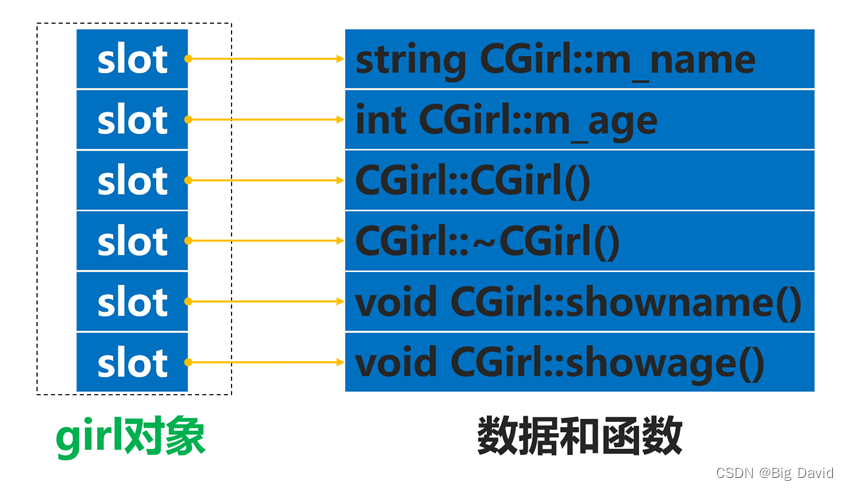
C++基础从0到1入门编程(四)类和对象
系统学习C 方便自己日后复习,错误的地方希望积极指正 往期文章: C基础从0到1入门编程(一) C基础从0到1入门编程(二) C基础从0到1入门编程(三) 参考视频: 1.黑马程序员匠心…...

如何有效解决UDP协议传输问题实现快速安全的文件传输
随着互联网技术的不断发展,UDP协议作为一种快速、简单的传输协议被广泛应用于文件传输领域。然而,UDP协议传输过程中也存在着一些问题,如传输速度不稳定、数据丢失等,这些问题会影响到文件传输的效率和安全性。本文将介绍UDP协议传…...
Mac下载的软件显示文件已损坏,如何解决文件已损坏问题,让文件可以正常运行
Mac下载的软件显示文件已损坏,如何解决文件已损坏问题,让文件可以正常运行 设备/引擎:Mac(11.6)/Mac Mini 开发工具:终端 开发需求:让显示已损坏的文件顺利安装到电脑 大家肯定都遇到过下载…...
实战 - 在Linux上部署各类软件
前言 为什么学习各类软件在Linux上的部署 在前面,我们学习了许多的Linux命令和高级技巧,这些知识点比较零散,同学们跟随着课程的内容进行练习虽然可以基础掌握这些命令和技巧的使用,但是并没有一些具体的实操能够串联起来这些知…...

Jenkins扩展篇-流水线脚本语法
JenkinsFile可以通过两种语法来声明流水线结构,一种是声明式语法,另一种是脚本式语法。 脚本式语法以Groovy语言为基础,语法结构同Groovy相同。 由于Groovy学习不适合所有初学者,所以Jenkins团队为编写Jenkins流水线提供一种更简…...

一个ETL流程搞定数据脱敏
数据脱敏是什么? 数据脱敏是指在数据处理过程中,通过一系列的技术手段去除或者替换敏感信息,以保护个人隐私和敏感信息的安全的过程。数据脱敏通常在数据共享、数据分析和软件测试等场景下使用,它旨在降低数据泄露和滥用的风险。…...
重生奇迹mu迹辅助什么好
主流辅助一号选手:弓箭手 智弓作为最老、最有资历的辅助职业,一直都是各类玩家的首要选择。因为智力MM提供的辅助能力都是最基础、最有效、最直观的辅助。能够减少玩家对于装备的渴求度,直接提升人物的攻防,大大降低了玩家升级打…...

【bug 回顾】上传图片超时
测试 bug 问题分析 - 上传图片超时 最近在测试上遇到一个莫名奇妙的问题,最后也没有得到具体是哪块的原因,看各位大佬有没有思路?? 一 、背景 现在我们有三台服务器,用来布两套环境。其中另外一台服务器3配置的 tom…...
Leetcode1410. HTML 实体解析器
Every day a Leetcode 题目来源:1410. HTML 实体解析器 解法1:模拟 遍历字符串 text,每次遇到 ’&‘,就判断以下情况: 双引号:字符实体为 " ,对应的字符是 " 。单引号&a…...

【Django使用】django经验md文档10大模块。第4期:Django数据库增删改查
Django的主要目的是简便、快速的开发数据库驱动的网站。它强调代码复用,多个组件可以很方便的以"插件"形式服务于整个框架,Django有许多功能强大的第三方插件,你甚至可以很方便的开发出自己的工具包。这使得Django具有很强的可扩展…...
SAP LU04记账更改通知单创建转储单报错:L3094 记帐修改没有份存在
解决办法: 使用事务码LU02,修改过账更改状态,将过账更改状态改为U,强制关闭 1. LU04 查找记账更改通知单号 2. 事务码LU02修改状态 这个时候再用LU04去查看的时候,就不会再显示了...
Redis:Java客户端
前言 "在当今大数据和高并发的应用场景下,对于数据缓存和高效访问的需求日益增长。而Redis作为一款高性能的内存数据库,以其快速的读写能力和丰富的数据结构成为众多应用的首选。与此同时,Java作为广泛应用于企业级开发的编程语言&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
