数学建模之拟合及其代码
发现新天地,欢迎访问Cr不是铬的个人网站
引言
与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合的最好(最小化损失函数)
最小二乘法
在一维线性拟合中,采用的是最小二乘法来求得最优拟合。
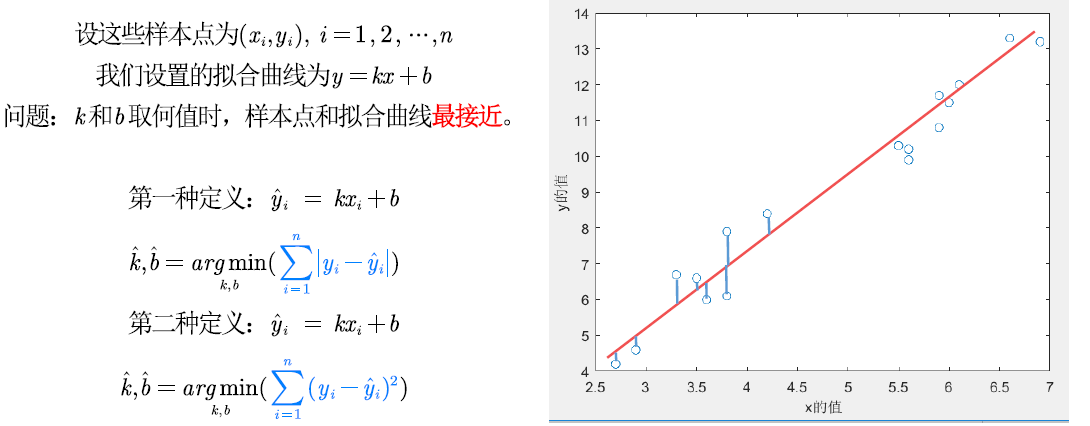
求解过程证明:

拟合好坏的评价
通过最小二乘法确定拟合方程后,怎么来评价拟合的好坏呢?
- SST:总体平方和
- SSE:误差平方和
- SSR: 回归平方和
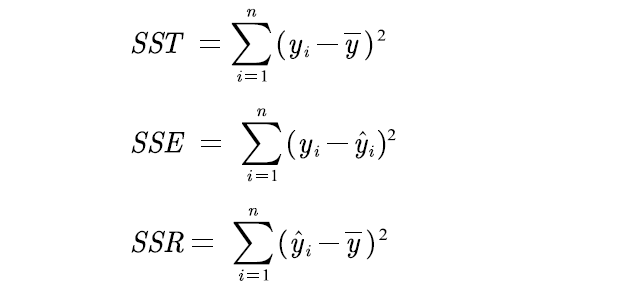
SST = SSE + SSR;
拟合优度:1 - SSE/SST.
R^2越接近1,说明误差平方和越接近0,误差越小说明拟合的越好
代码部分
最小二乘
%% 开始拟合
%行数
n = size(x,1);
%计算拟合参数
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法:模拟生成x和y的序列,比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 ; % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b; % k和b都是已知值
% plot(xx,yy,'-')
匿名函数用法
% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围% f=@(x) k*x+b;
% fplot(f,[2.5,7]);
拟合优度
%% 求拟合度
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST完整代码
%% 导入数据
load data
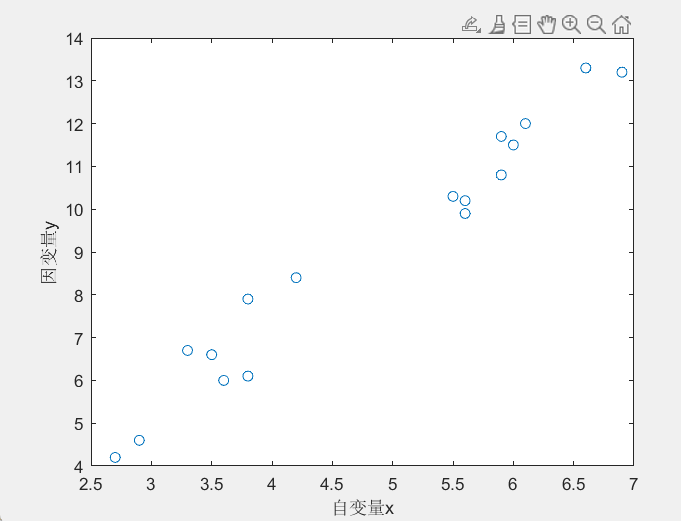
%绘制原始散点图
plot(x,y,'o')
%给x轴与y轴加上标签
xlabel('自变量x')
ylabel('因变量y')
%% 开始拟合
%行数
n = size(x,1);
%计算拟合参数
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法:模拟生成x和y的序列,比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 ; % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b; % k和b都是已知值
% plot(xx,yy,'-')% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数,可以是一个,也可以是多个,用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
% z=@(x,y) x^2+y^2;
% z(1,2)
% % ans = 5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval = [xmin xmax] 表示定义域的范围% f=@(x) k*x+b;
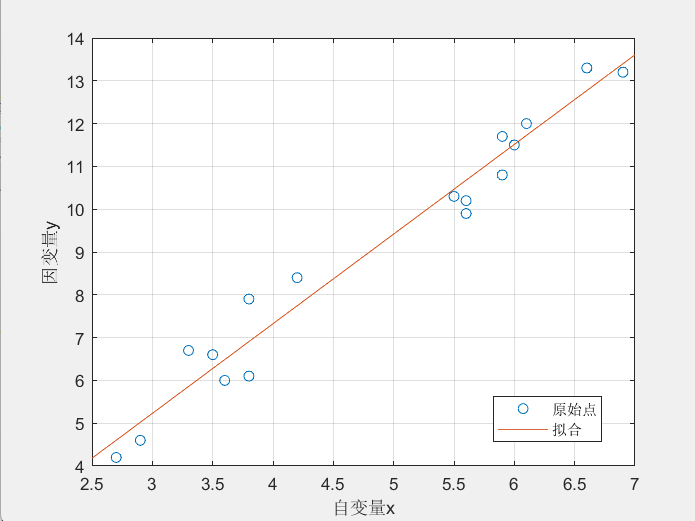
% fplot(f,[2.5,7]);f = @(x) k*x + b;
fplot(f,[2.5,7.0])
legend('原始点','拟合')
%% 求拟合度
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2) % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR % 5.6843e-14 = 5.6843*10^-14 matlab浮点数计算的一个误差
R_2 = SSR / SST本文由博客一文多发平台 OpenWrite 发布!
相关文章:

数学建模之拟合及其代码
发现新天地,欢迎访问Cr不是铬的个人网站 引言 与插值问题不同,在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数(曲线),使得该曲线在某种准则下与所有的数据点最为接近,即曲线拟合…...
GeoTrust SSL数字安全证书介绍
一、GeoTrust OV证书的介绍 GeoTrust OV证书是由GeoTrust公司提供的SSL证书,它是一种支持OpenSSL的数字证书,具有更高的安全性和可信度。GeoTrust是全球领先的网络安全解决方案提供商,为各类用户提供SSL证书和信任管理服务。GeoTrust OV证书…...
【C++上层应用】5. 文件和流
文章目录 【 1. 打开文件 】1.1 open 函数1.2 open 多种模式的结合使用 【 2. 关闭文件 】【 3. 写入 & 读取文件 】【 4. 文件位置指针 】 和 iostream 库中的 cin 标准输入流和 cout 标准输出流类似,C中另一个库 fstream 也存在文件的读取流和标准写入流。fst…...

JAVA爬虫1 - HttpClient的使用
一、简介 HttpClient 是 Apache Jakarta Common 下的子项目,用来提供高效的、最新的、功能丰富的支持 HTTP协议的客户端编程工具包,并且它支持HTTP协议最新的版本和建议。HttpClient已经应用在很多的 项目中,比如Apache Jakarta上很著名的另外两个开源项目Cactus和HTMLUnit…...

NX二次开发UF_CSYS_map_point 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CSYS_map_point Defined in: uf_csys.h int UF_CSYS_map_point(int input_csys, double input_point [ 3 ] , int output_csys, double output_point [ 3 ] ) overview 概述 Ma…...

Spring Web MVC
目录 一.简介 二.建立连接(客户端和服务器) 三.请求 1.传递单个参数 2.传递多个参数 3.对象 4.数组/集合 5.JSON 6.URL参数 7.上传文件 8.获取cookie和session (1)获取cookie (2)获取session …...
Debian系列的Linux发行版上部署wvp
Debian系列的Linux发行版上部署wvp 环境搭建1.Debian系列的Linux发行版上安装nginx2.安装mysql设置mysql密码修改权限sudo mysql ERROR 1045 (28000): Access denied for user root@localhost (using password: NO)配置相关navicat 连接不上 报错 10061navicat 连接报错 1130 -…...

无人智能柜:经营成本低,运维智能化
在现代商业领域中,无人智能柜正逐渐崭露头角,成为一种具有前景的商业模式。其独特之处在于经营成本的低廉性和运维过程的智能化。相较于传统的便利店等实体店铺,无人智能柜在运营过程中不仅能够降低成本,还能够实现高效的运维管理…...
java.lang.UnsupportedOperationException 关于Arrays.asList问题解决
解析String 字符串为List集合ArrayList<String> itemsList Arrays.asList(items.split("\\|")List<String> itemsList Arrays.asList(items.split("\\|")final Iterator<String> iterator itemsList.iterator();while (iterator.hasNex…...
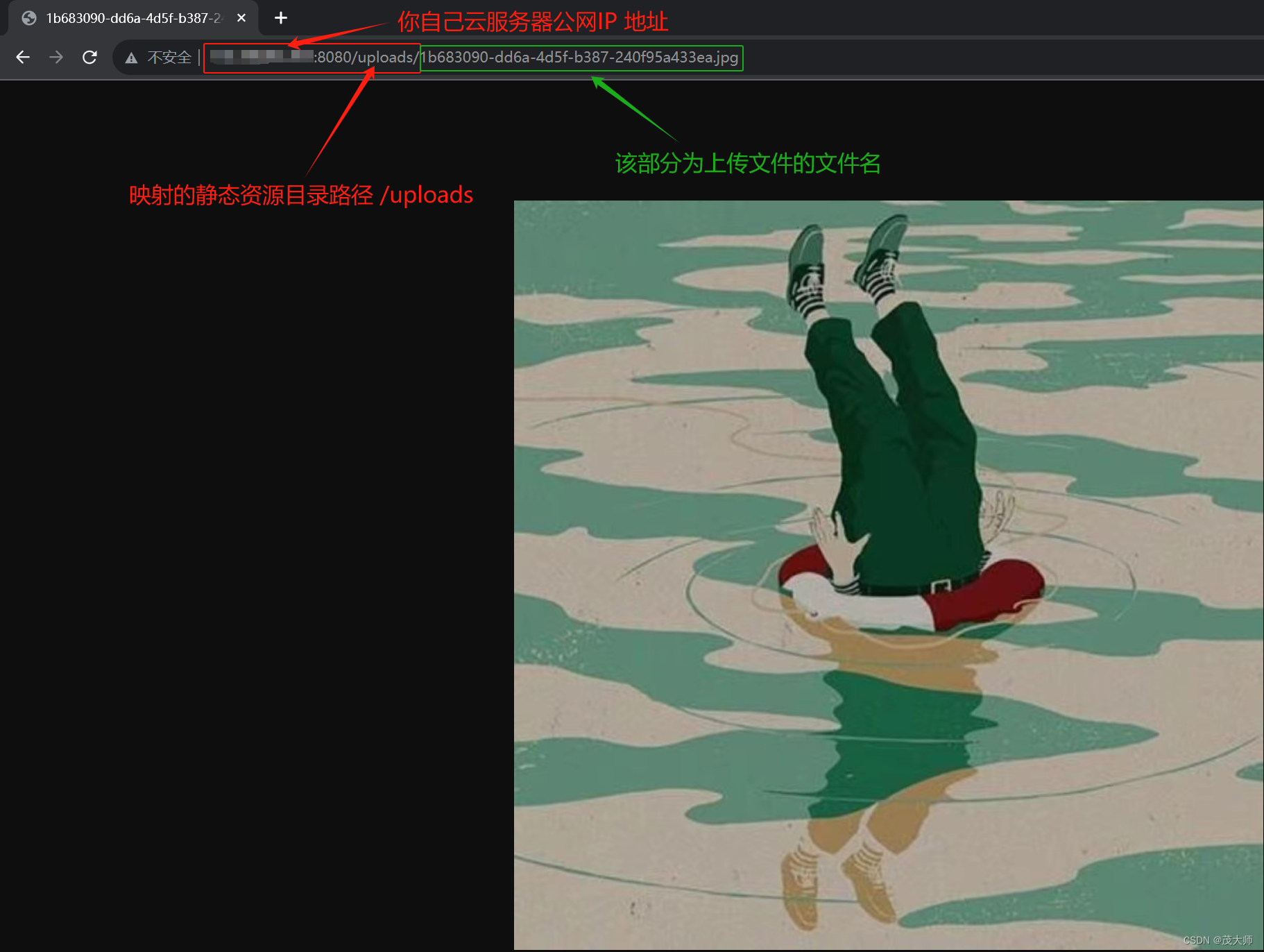
2023.11.23 云服务器实现 Spring Boot 项目文件上传并访问
环境介绍 云服务器:京东云云服务器系统: CentOS 7.9JDK 版本:1.8Spring Boot 版本:2.7.17 具体步骤 步骤一 首先我们得先创建一个 Spring Boot 项目 创建如下目录结构 关于如何创建一个 Spring Boot 项目 请点击下方链接详细了解 …...

SAP实现多个统御科目:特殊总账SGL+备选统驭科目Alternative Reconciliation Accounts
以前只知道特别总账。学习了 客商的每个公司视图主数据唯一分配一个统驭科目。一般情况下,客商经常发生的业务对应的总帐科目设为统驭科目。 客户设置的统驭科目:应收账款 供应商设置的统驭科目:应付账款 除了经常的销售和采购业务对应应收和…...
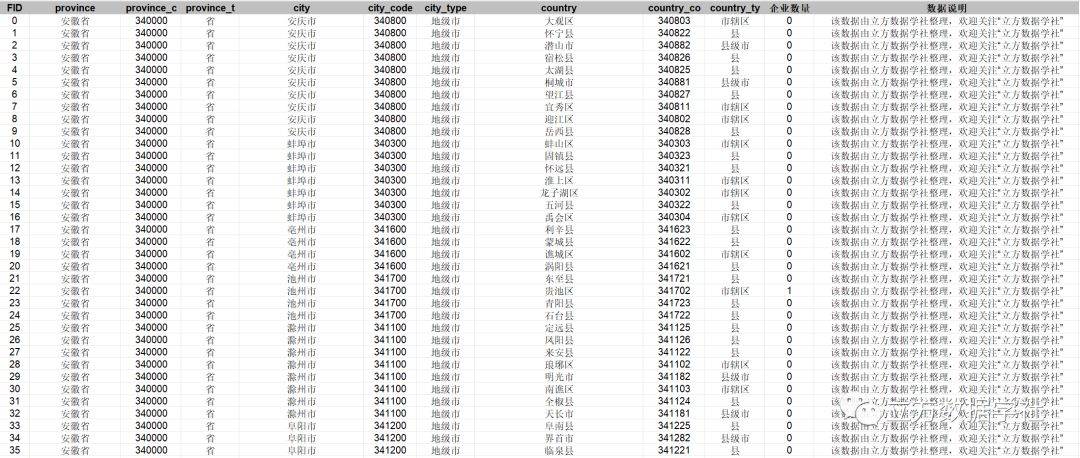
【数据分享】2023年我国省市县三级的瞪羚企业数量(免费获取/Excel/Shp格式)
企业是经济活动的参与主体。一个城市的企业数量决定了这个城市的经济发展水平!比如一个城市的金融企业较多,那这个城市的金融产业肯定比较发达;一个城市的制造业企业较多,那这个城市的制造业肯定比较发达。 之前我们给大家分享了…...
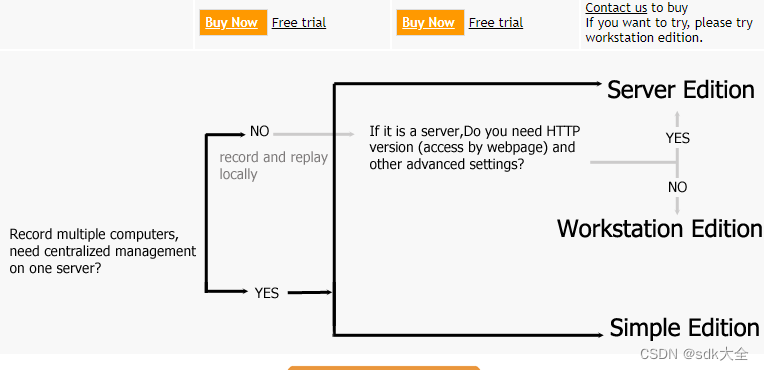
用于计算机屏幕安全摄像头系统:Screen Anytime Crack
Screen Anytime 是一款软件,旨在自动将整个用户会话或 PC/服务器/VM/Kiosk 的 /RDP/Citrix/RemoteApp 会话的屏幕活动记录到视频日志文件中,以用于记录、审核和监控目的。通过重播其高度压缩的视频,您可以轻松回顾单台计算机或一组服务器/PC …...
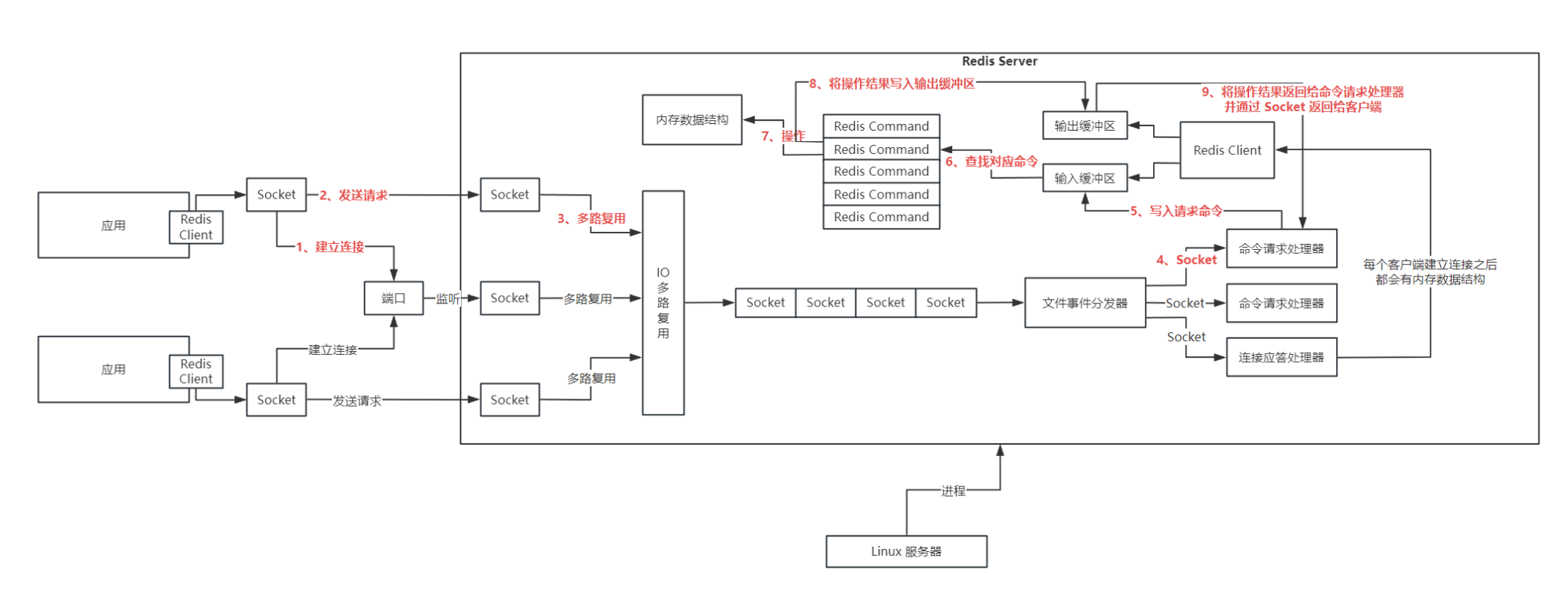
Redis深入理解-Socket连接建立流程以及文件事件处理机制
Redis Server 运行原理图 Redis 服务器中 Socket 网络建立以及文件事件模型 一个 redis 单机,可以抗几百上千的并发,这里的并发指的就是同时可以有几百个 client 对这个 redis server 发起请求,都需要去建立网络连接,同时间可能会…...

Docker run 命令
docker run :创建一个新的容器并运行一个命令 语法 docker run [OPTIONS] IMAGE [COMMAND] [ARG...]OPTIONS说明: -a stdin:指定标准输入输出内容类型,可选STDIN/STDOUT/STDERR三项; -d:后台运行容器&am…...

Vue中的$nextTick的作用
在 Vue 中,当某些数据发生变化时,DOM 并不会立即更新。相反,Vue 会在下一个事件循环周期(microtask)中异步执行更新,这样可以避免频繁的 DOM 操作。然而,有时候我们需要在 DOM 更新后执行一些操…...

浅谈Linux bash脚本----getopts获取脚本POSIX标准传参
getopts是一个在 Shell 脚本中用于解析命令行选项的内置命令。 它用于处理脚本的参数,使得脚本可以接受不同的选项和参数,并根据用户提供的输入采取相应的操作。 getopts 命令基于 POSIX 标准,并且通常与 while 循环结合使用。它的语法如下…...
PyCharm玩转ESP32
想必玩ESP32的童鞋都知道Thonny,当然学Python的童鞋用的更多的可能是PyCharm和VsCode Thonny和PyCharm的对比 对于PyCharm和VsCode今天不做比较,今天重点说一下用PyCharm玩转ESP32,在这之前我们先对比下Thonny和PyCharm的优缺点 1、使用Tho…...

uniapp自定义导航栏返回按键
目录 htmljscss最后 html <!-- #ifdef MP-WEIXIN || APP-PLUS --> <view class"tc header":style"topBarHeight() 0 ? : height: topBarHeight() px;padding-top: topBarTop() px"><view class"reg180" :style"top…...

「可移动工具车」物料管理的得力助手
随着工业制造企业不断发展,仓储的运营变得越来越重要,物料高效管理也迎来了新的挑战,工厂物料管理直接影响着生产效率和成本控制,不合理的物料管理可能导致物料溢出、过度库存、损耗增加等问题,进而影响企业的整体竞争…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
