【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量
【Python】Numpy–np.linalg.eig()求对称矩阵的特征值和特征向量
文章目录
- 【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量
- 1. 介绍
- 2. API
- 3. 代码示例
1. 介绍
特征分解(Eigendecomposition),又称谱分解(Spectral decomposition)是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。
- 需要注意:只有对可对角化矩阵才可以施以特征分解。
- 当方阵的行列式不为0时,它才可以特征分解。
- 对称矩阵的行列式不为0。故实对称矩阵 A 可被分解成:
A=QΛQTA = QΛ Q^T A=QΛQTΛ是特征值构成的对角矩阵,Q为特征向量构成的矩阵(每列为一个特征向量)。
2. API
Numpy提供了丰富的API:
- 求矩阵的特征值和特征向量;
- 求矩阵的行列式
- 求方阵的逆
import numpy as np
# 计算特征值和特征向量
x, V = np.linalg.eig(A)# 计算矩阵的行列式
det = np.linalg.det(A)# 计算方阵的逆
A_inv = np.linalg.inv(A)
3. 代码示例
import numpy as npA = np.array([[0, 1, 2, 3],[1, 0, 3, 1],[2, 3, 0, 2],[3, 1, 2, 0]])x, V = np.linalg.eig(A)V_inv = np.linalg.inv(V)print('A的行列式', np.linalg.det(A))# 注意这里:且不可使用‘*’做乘法(因为*优先使用点乘,点乘不成立,才会进行矩阵乘法)
B = np.matmul(np.matmul(V, np.diag(x)), (V_inv))print('特征值x: \n', x)print('特征向量V: \n', V)print('V_T: \n', V.T)print('V_inv: \n', V_inv)print('B: \n', B)-----------------------------输出-----------------------------------
A的行列式 9.000000000000009
特征值x:[ 6.05572176 0.15432761 -3. -3.21004937]
特征向量V:[[-5.03020107e-01 -4.75446017e-01 -7.07106781e-01 -1.44643895e-01][-4.38300211e-01 6.51958757e-01 -2.36695808e-17 -6.18742842e-01][-5.49394638e-01 3.50502424e-01 -1.50578103e-16 7.58494287e-01][-5.03020107e-01 -4.75446017e-01 7.07106781e-01 -1.44643895e-01]]
V_T:[[-5.03020107e-01 -4.38300211e-01 -5.49394638e-01 -5.03020107e-01][-4.75446017e-01 6.51958757e-01 3.50502424e-01 -4.75446017e-01][-7.07106781e-01 -2.36695808e-17 -1.50578103e-16 7.07106781e-01][-1.44643895e-01 -6.18742842e-01 7.58494287e-01 -1.44643895e-01]]
V_inv:[[-5.03020107e-01 -4.38300211e-01 -5.49394638e-01 -5.03020107e-01][-4.75446017e-01 6.51958757e-01 3.50502424e-01 -4.75446017e-01][-7.07106781e-01 -8.99464510e-16 8.86986655e-16 7.07106781e-01][-1.44643895e-01 -6.18742842e-01 7.58494287e-01 -1.44643895e-01]]
B:
[[ 1.71102595e-15 1.00000000e+00 2.00000000e+00 3.00000000e+00][ 1.00000000e+00 9.30160211e-16 3.00000000e+00 1.00000000e+00][ 2.00000000e+00 3.00000000e+00 -2.20312258e-16 2.00000000e+00][ 3.00000000e+00 1.00000000e+00 2.00000000e+00 1.88043220e-15]]
相关文章:
求对称矩阵的特征值和特征向量)
【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量
【Python】Numpy–np.linalg.eig()求对称矩阵的特征值和特征向量 文章目录【Python】Numpy--np.linalg.eig()求对称矩阵的特征值和特征向量1. 介绍2. API3. 代码示例1. 介绍 特征分解(Eigendecomposition),又称谱分解(Spectral d…...
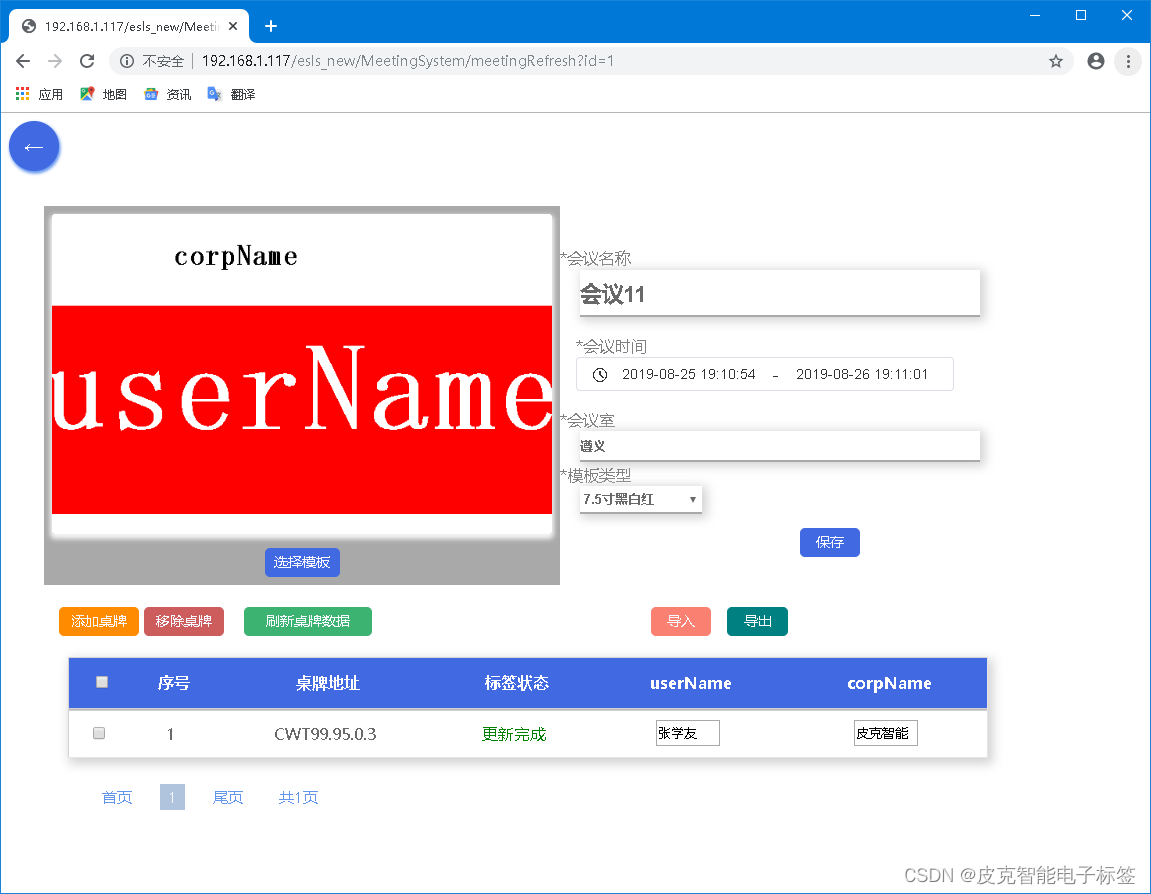
医疗床头卡(WIFI方案)
一、产品特性 7.5寸墨水屏显示WIFI无线通信,极简部署,远程控制按键及高亮LED指示灯指示800*480点阵屏幕锂电池供电,支持USB充电DIY界面支持文本/条码/二维码/图片超低功耗/超长寿命,一次充电可用一年基于现有Wifi环境,…...
[YOLO] yolo博客笔记汇总(自用
pip下载速度太慢,国内镜像: 国内镜像解决pip下载太慢https://blog.csdn.net/weixin_51995286/article/details/113972534 YOLO v2和V3 关于设置生成anchorbox,Boundingbox边框回归的过程详细解读 YOLO v2和V3 关于设置生成an…...
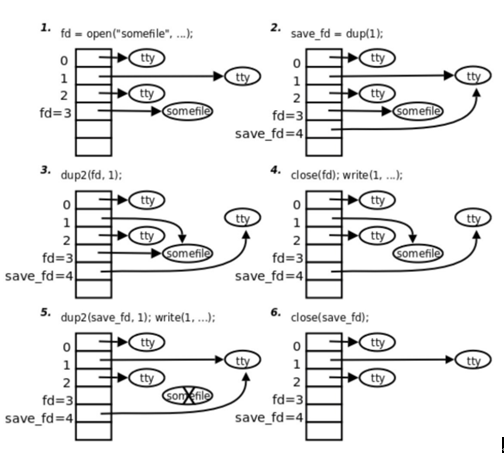
Linux 常用 API 函数
文章目录1. 系统调用与库函数1.1 什么是系统调用1.2 系统调用的实现1.3 系统调用和库函数的区别2. 虚拟内存空间3. 错误处理函数4. C 库中 IO 函数工作流程5. 文件描述符6. 常用文件 IO 函数6.1 open 函数6.2 close 函数6.3 write 函数6.4 read 函数6.5 lseek 函数7. 文件操作相…...
【转载】bootstrap自定义样式-bootstrap侧边导航栏的实现
bootstrap自带的响应式导航栏是向下滑动的,但是有时满足不了个性化的需求: 侧滑栏使用定位fixed 使用bootstrap响应式使用工具类 visible-sm visible-xs hidden-xs hidden-sm等对不同屏幕适配 侧滑栏的侧滑效果不使用jquery方法来实现,使用的是css3 tr…...

奇瑞x华为纯电智选车来了,新版ADS成本将大幅下降
作者 | 德新 编辑 | 于婷HiEV获悉,问界M5将在4月迎来搭载高阶辅助驾驶的新款,而M9将在今年秋天发布。 奇瑞一侧,华为将与奇瑞首先推出纯电轿车,代号EH3。新车将在奇瑞位于芜湖江北新区的智能网联超级二工厂组装下线。目前超级二工…...
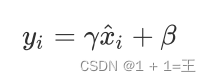
机器学习的特征归一化Normalization
为什么需要做归一化? 为了消除数据特征之间的量纲影响,就需要对特征进行归一化处理,使得不同指标之间具有可比性。对特征归一化可以将所有特征都统一到一个大致相同的数值区间内。 为了后⾯数据处理的⽅便,归⼀化可以避免⼀些不…...
程序员看过都说好的资源网站,看看你都用过哪些?
程序员必备的相关资源网站一.图片专区1.表情包(1)发表情(2)逗比拯救世界(3)搞怪图片生成(4)哇咔工具2.图标库(1)Font Awesome(2)iconf…...
Win11的两个实用技巧系列之设置系统还原点的方法、安全启动状态开启方法
Win11如何设置系统还原点?Win11设置系统还原点的方法很多用户下载安装win11后应该如何创建还原点呢?现在我通过这篇文章给大家介绍一下Win11如何设置系统还原点?在Windows系统中有一个系统还原功能可以帮助我们在电脑出现问题的时候还原到设置的时间上&…...
【Linux】项目的自动化构建-make/makefile
💣1.背景会不会写makefile,从一个侧面说明了一个人是否具备完成大型工程的能力 一个工程中的源文件不计数,其按类型、功能、模块分别放在若干个目录中,makefile定义了一系列的 规则来指定,哪些文件需要先编译ÿ…...

【Redis学习2】Redis常用数据结构与应用场景
Redis常用数据结构与应用场景 redis中存储数据是以key-value键值对的方式去存储的,其中key为string字符类型,value的数据类型可以是string(字符串)、list(列表)、hash(字典)、set(集合) 、 zset(有序集合)。 这5种数据类型在开发中可以应对大部分场景的…...

踩了大坑:https 证书访问错乱
文章目录一、问题排查及解决问题一:证书加载错乱问题二:DNS 解析污染问题问题三:浏览器校验问题二、终极解决方法2.1 可外网访问域名2.2 只能内网访问域名2.3 内网自动化配置2.4 错误解决一、问题排查及解决 今天遇到这样一个问题࿰…...
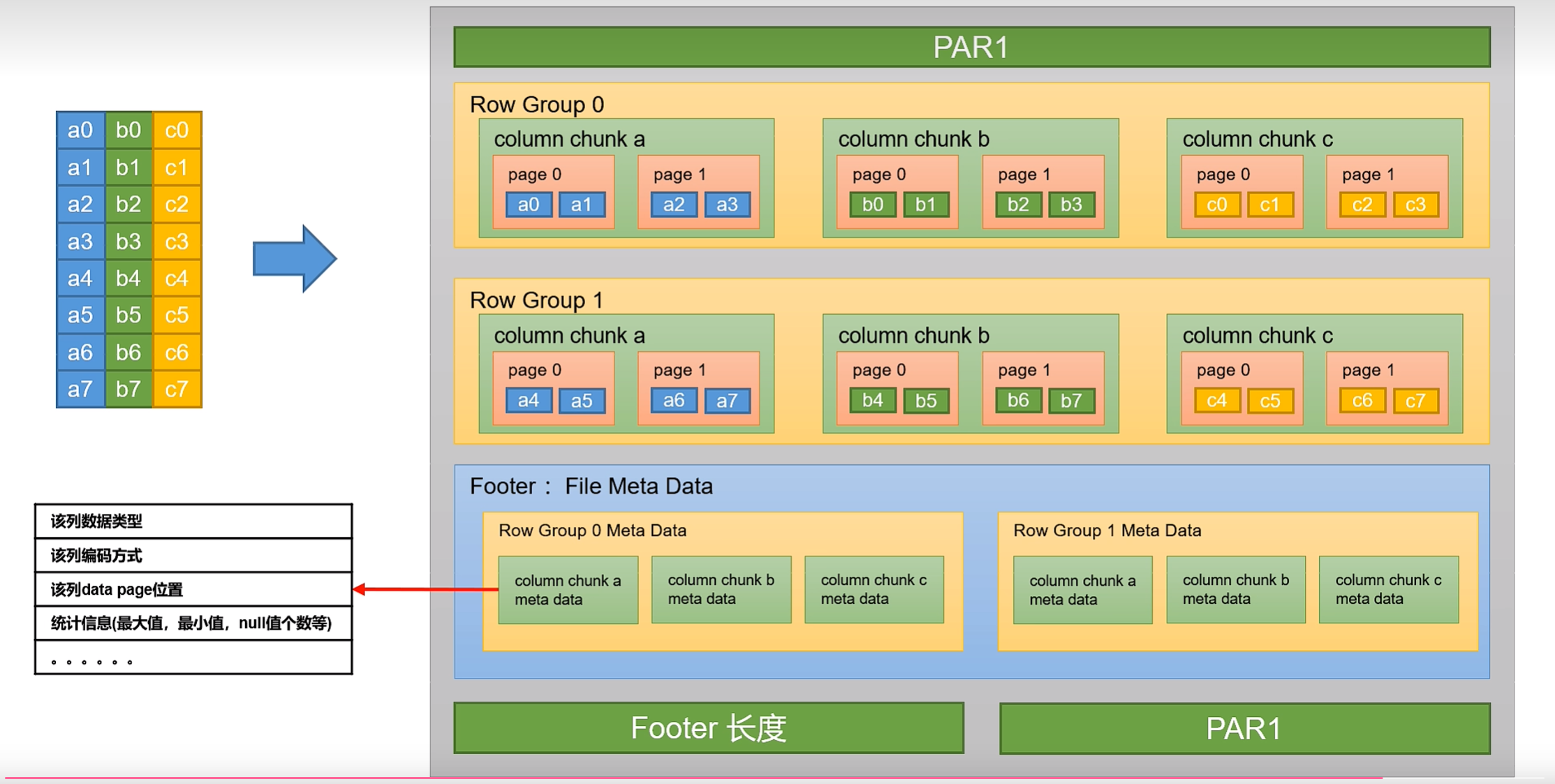
大数据技术之Hive(四)分区表和分桶表、文件格式和压缩
一、分区表和分桶表1.1 分区表partitionhive中的分区就是把一张大表的数据按照业务需要分散的存储到多个目录,每个目录就称为该表的一个分区。在查询时通过where子句中的表达式选择式选择查询所需要的分区,这样的查询效率辉提高很多。1.1.1 分区表基本语…...

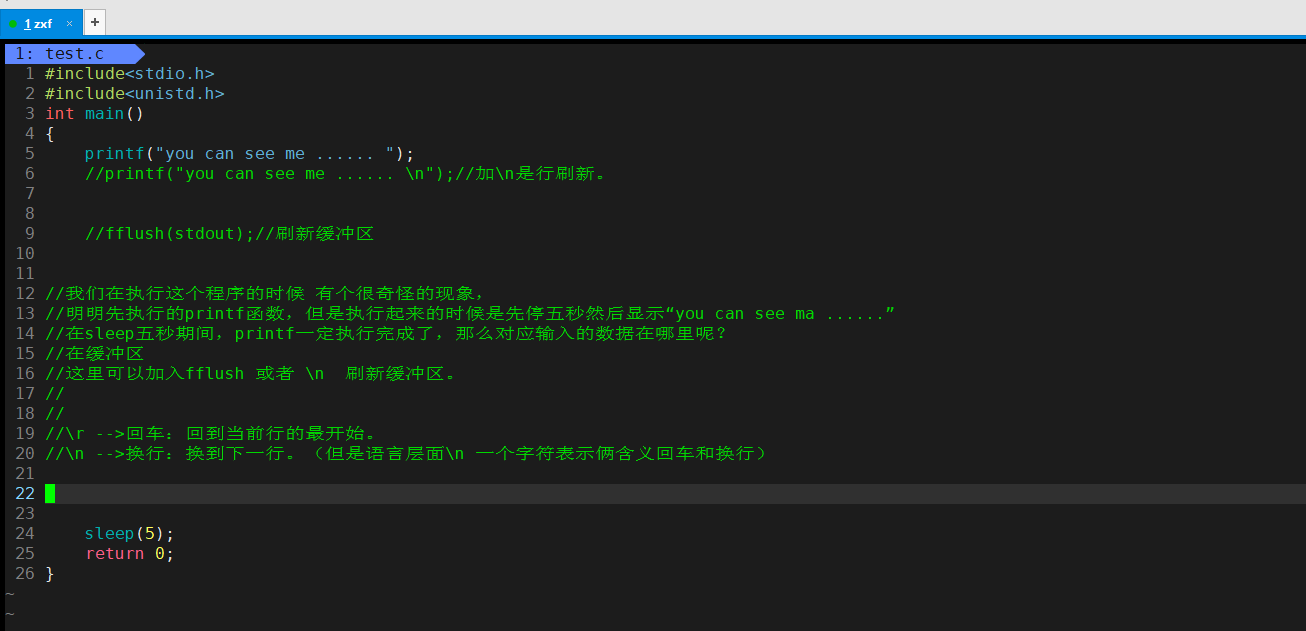
环形缓冲区(c语言)
1、概念介绍 在我们需要处理大量数据的时候,不能存储所有的数据,只能先处理先来的,然后将这个数据释放,再去处理下一个数据。 如果在一个线性的缓冲区中,那些已经被处理的数据的内存就会被浪费掉。因为后面的数据只能…...
创建自助服务知识库的指南
在SaaS领域,自助文档是你可以在客户登录你的网站时为他们提供的最灵活的帮助方式,简单来说,一个自助知识库是一个可以帮助许多客户的文档,拥有出色的自助服务知识库,放在官网或者醒目的地方,借助自助服务知…...

分层测试(1)分层测试是什么?【必备】
1. 什么是分层测试? 分层测试是通过对质量问题分类、分层来保证整体系统质量的测试体系。 模块内通过接口测试保证模块质量,多模块之间通过集成测试保证通信路径和模块间交互质量,整体系统通过端到端用例对核心业务场景进行验证,…...

开源ZYNQ AD9361软件无线电平台
(1) XC7Z020-CLG400 (2) AD9363 (3) 单发单收,工作频率400MHz-2.7GHz (4) 发射带PA,最大输出功率约20dbm (5) 接收带LNA,低…...
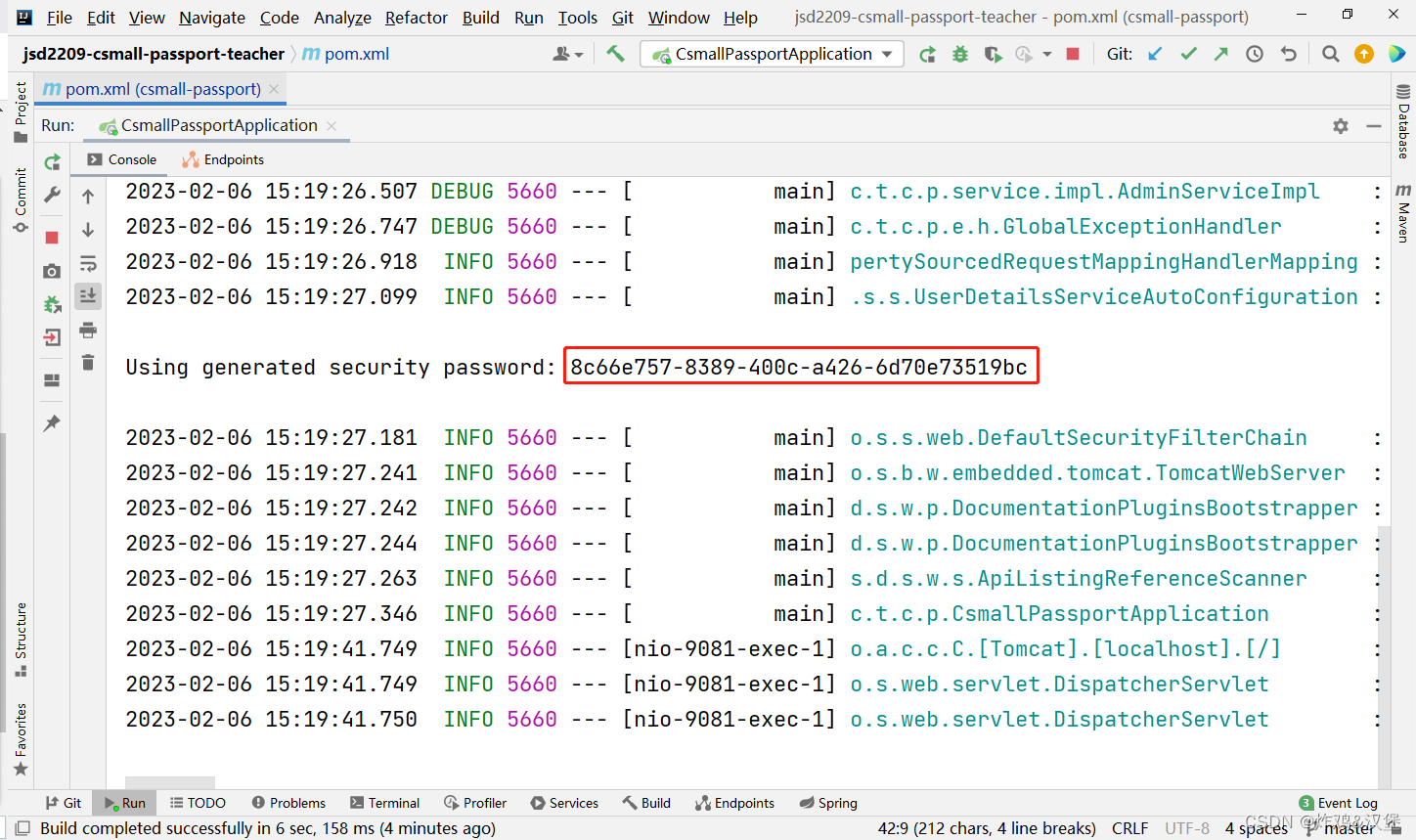
第四阶段-12关于Spring Security框架,RBAC,密码加密原则
关于csmall-passport项目 此项目主要用于实现“管理员”账号的后台管理功能,主要实现: 管理员登录添加管理员删除管理员显示管理员列表启用 / 禁用管理员 关于RBAC RBAC:Role-Based Access Control,基于角色的访问控制 在涉及…...

JPA——Date拓展之Calendar
Java Calendar 是时间操作类,Calendar 抽象类定义了足够的方法,在某一特定的瞬间或日历上,提供年、月、日、小时之间的转换提供方法 一、获取具体时间信息 1. 当前时间 获取此刻时间的年月日时分秒 Calendar calendar Calendar.getInstance(); int …...

一文吃透 Spring 中的 AOP 编程
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
