第一类曲线积分@对弧长的曲线积分
文章目录
- abstract
- 对弧长的曲线积分
- 曲线形构件的质量
- 第一类曲线积分
- 曲线积分存在性
- 利用曲线积分的定义描述曲线形构件质量问题
- 推广
- 曲线积分可加性
- 闭曲线积分
- 曲线积分性质
- 曲线积分的计算方法
- 证明(部分推导)
- 小结
- 曲线弧显函数形式方程下的曲线积分公式
- 推广
- 例
- 例
- 例
abstract
- 在积分学中,积分范围先是从数轴上(直线)的一个区间的情形,推广到平面或看空间内的一个闭区域的情形
- 不仅如此,积分概念可以推广到积分范围为一段曲线弧或一片曲面的情形,分别称为曲线积分和曲面积分
对弧长的曲线积分
曲线形构件的质量
- 对弧长的曲线积分源自某些问题的研究,其中最经典的一个问题模型是曲线形构建的质量问题
- 在讨论定积分和二重积分时,分别对应曲边梯形面积问题和曲顶柱体的体积问题
- 而理解曲线积分时,用类似理解定积分时的几何的角度就不容易,也不太合适,而从物理意义角度就比较合适
- 通过对这个问题问题模型的抽象,定义出弧长的曲线积分(第一类曲线积分)
第一类曲线积分
- 定义:设 L L L为 x O y xOy xOy面内的一条光滑曲线弧,函数 f ( x , y ) f(x,y) f(x,y)在 L L L上有界,在 L L L上任意插入一系列点 M 1 , ⋯ , M n − 1 M_1,\cdots,M_{n-1} M1,⋯,Mn−1,把 L L L分成 n n n个小段
- 设第 i i i小段的长度为 Δ s i \Delta{s_i} Δsi,又 ( ξ i , η i ) (\xi_i,\eta_i) (ξi,ηi)为第 i i i个小段上任意取定的,作乘积 f ( ξ i , η i ) Δ s i f(\xi_i,\eta_i)\Delta{s_i} f(ξi,ηi)Δsi
(0), ( i = 1 , 2 , ⋯ , n ) (i=1,2,\cdots,n) (i=1,2,⋯,n),并作和式 ∑ i = 1 n f ( ξ i , η i ) Δ s i \sum_{i=1}^{n}f(\xi_i,\eta_i)\Delta{s_i} ∑i=1nf(ξi,ηi)Δsi(1) - 若当各个小弧段的长度的最大值 λ → 0 \lambda\to{0} λ→0时,式(1)的极限总存在,切曲线弧 L L L的分法以及点 ( ξ i , η i ) (\xi_i,\eta_i) (ξi,ηi)的取法无关,则称此极限为函数 f ( x , y ) f(x,y) f(x,y)在曲线弧 L L L上对弧长的曲线积分或第一类曲线积分,记为 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds,即 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \lim\limits_{\lambda\to{0}} \sum_{i=1}^{n}f(\xi_i,\eta_i)\Delta{s_i} λ→0lim∑i=1nf(ξi,ηi)Δsi
(3) - 其中 f ( x , y ) f(x,y) f(x,y)称为被积函数, L L L称为积分弧段(积分弧段类似于定积分的积分区间或重积分的积分区域)
- 而弧段元素 Δ s i \Delta{s_i} Δsi或 d s \mathrm{d}s ds类似于定积分 ∫ a b f ( x ) d x \int_{a}^{b}f(x)\mathrm{d}x ∫abf(x)dx中的区间元素 d x \mathrm{d}x dx
- Note: f ( x , y ) f(x,y) f(x,y)和 L L L的方程是相对独立的,最简单的情形是
- f ( x , y ) f(x,y) f(x,y)为常数
- L L L为直线方程
曲线积分存在性
-
当 f ( x , y ) f(x,y) f(x,y)在光滑曲线弧 L L L上连续时,对弧长的曲线积分 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds总是存在的
- 在讨论曲线积分时,我们总假定 f ( x , y ) f(x,y) f(x,y)在 L L L上是连续的
-
函数在曲线上连续表示?(TODO)
利用曲线积分的定义描述曲线形构件质量问题
- 根据上述定义,曲线形构件的质量 m m m当线密度 μ ( x , y ) \mu(x,y) μ(x,y)在 L L L上连续时,就有等于 μ ( x , y ) \mu(x,y) μ(x,y)对弧长的曲线积分,即 m = ∫ L μ ( x , y ) d s m=\int_{L}\mu(x,y)\mathrm{d}s m=∫Lμ(x,y)ds
(4)
推广
- 上述曲线积分的定义是平面曲线积分,可以类似地推广到积分弧段为空间曲线 Γ \Gamma Γ的情形,即函数 f ( x , y , z ) f(x,y,z) f(x,y,z)在曲线弧 Γ \Gamma Γ上对弧长的曲线积分 ∫ Γ f ( x , y , z ) d s \int_{\Gamma}f(x,y,z)\mathrm{d}s ∫Γf(x,y,z)ds= lim λ → 0 ∑ i = 1 n f ( ξ i , η i , ξ i ) Δ s i \lim\limits_{\lambda\to{0}}\sum_{i=1}^{n}f(\xi_i,\eta_i,\xi_i)\Delta{s_i} λ→0lim∑i=1nf(ξi,ηi,ξi)Δsi
(5)- f ( x , y , z ) f(x,y,z) f(x,y,z)可以表示空间中坐标为 x , y , z x,y,z x,y,z的点处的密度(点附近小区域密度的代表值)
曲线积分可加性
- 若 L L L是分段光滑的(有限个点不光滑),则规定函数在 L L L上的曲线积分等于函数在光滑的各段上的曲线积分之和(空间曲线 Γ \Gamma Γ也类似)
- 例如设 L L L可分成两段光滑曲线弧 L 1 L_1 L1以及 L 2 L_2 L2,记为 L = L 1 + L 2 L=L_1+L_2 L=L1+L2),就规定 ∫ L 1 + L 2 f ( x , y ) d s \int_{L_1+L_2}f(x,y)\mathrm{d}s ∫L1+L2f(x,y)ds= ∫ L 1 f ( x , y ) d s \int_{L_1}f(x,y)\mathrm{d}s ∫L1f(x,y)ds+ ∫ L 2 f ( x , y ) d s \int_{L_2}f(x,y)\mathrm{d}s ∫L2f(x,y)ds
(6)
闭曲线积分
- 若 L L L是闭曲线,则函数 f ( x , y ) f(x,y) f(x,y)在闭曲线 L L L上对弧长的曲线积分记为 ∮ f ( x , y ) d s \oint{f(x,y)\mathrm{d}s} ∮f(x,y)ds
曲线积分性质
- 由对弧长的曲线积分的定义可知,其具有如下性质(这些性质和定积分类似)
- 线性性
- ∫ L [ α f ( x , y ) + β g ( x , y ) ] d s \int_{L}[\alpha f(x,y)+\beta{g(x,y)}]\mathrm{d}s ∫L[αf(x,y)+βg(x,y)]ds= α ∫ L f ( x , y ) d s \alpha\int_{L}f(x,y)\mathrm{d}s α∫Lf(x,y)ds+ β ∫ L g ( x , y ) d s \beta\int_{L}g(x,y)\mathrm{d}s β∫Lg(x,y)ds
(7)
- ∫ L [ α f ( x , y ) + β g ( x , y ) ] d s \int_{L}[\alpha f(x,y)+\beta{g(x,y)}]\mathrm{d}s ∫L[αf(x,y)+βg(x,y)]ds= α ∫ L f ( x , y ) d s \alpha\int_{L}f(x,y)\mathrm{d}s α∫Lf(x,y)ds+ β ∫ L g ( x , y ) d s \beta\int_{L}g(x,y)\mathrm{d}s β∫Lg(x,y)ds
- 可加性
- 若积分弧段 L L L可分为两段光滑曲线弧 L 1 , L 2 L_1,L_2 L1,L2,则
- ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= ∫ L 1 f ( x , y ) d s \int_{L_1}f(x,y)\mathrm{d}s ∫L1f(x,y)ds+ ∫ L 2 f ( x , y ) d s \int_{L_2}f(x,y)\mathrm{d}s ∫L2f(x,y)ds
(8)
- 设 L L L上 f ( x , y ) ⩽ g ( x , y ) f(x,y)\leqslant{g(x,y)} f(x,y)⩽g(x,y),则
- ∫ L f ( x , y ) d s ⩽ ∫ L g ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s\leqslant{\int_{L}g(x,y)\mathrm{d}s} ∫Lf(x,y)ds⩽∫Lg(x,y)ds
(9) - ∣ ∫ L f ( x , y ) d s ∣ ⩽ ∫ L ∣ f ( x , y ) ∣ d s |\int_{L}f(x,y)\mathrm{d}s| \leqslant{\int_{L}|f(x,y)|\mathrm{d}s} ∣∫Lf(x,y)ds∣⩽∫L∣f(x,y)∣ds
(10)- 因为 − ∣ f ( x , y ) ∣ ⩽ f ( x , y ) ⩽ ∣ f ( x , y ) ∣ -|f(x,y)|\leqslant{f(x,y)}\leqslant{|f(x,y)|} −∣f(x,y)∣⩽f(x,y)⩽∣f(x,y)∣
- − ∫ L ∣ f ( x , y ) ∣ d s ⩽ ∫ L f ( x , y ) d s ⩽ ∫ L ∣ f ( x , y ) ∣ d s -\int_{L}|f(x,y)|\mathrm{d}s\leqslant\int_{L}f(x,y)\mathrm{d}s\leqslant{\int_{L}|f(x,y)|\mathrm{d}s} −∫L∣f(x,y)∣ds⩽∫Lf(x,y)ds⩽∫L∣f(x,y)∣ds
- 改写成绝对值不等式即得证不等式
- ∫ L f ( x , y ) d s ⩽ ∫ L g ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s\leqslant{\int_{L}g(x,y)\mathrm{d}s} ∫Lf(x,y)ds⩽∫Lg(x,y)ds
曲线积分的计算方法
- 定理:设 f ( x , y ) f(x,y) f(x,y)在曲线弧 L L L上有定义且连续**, L L L的参数方程**为 x = ϕ ( t ) x=\phi(t) x=ϕ(t); y = ψ ( t ) y=\psi(t) y=ψ(t), t ∈ [ α , β ] t\in[\alpha,\beta] t∈[α,β]
- 若 ϕ ( t ) , ψ ( t ) \phi(t),\psi(t) ϕ(t),ψ(t)在 [ α , β ] [\alpha,\beta] [α,β]上具有一阶连续导数,且 ϕ ′ 2 + ψ ′ 2 ( t ) ≠ 0 \phi'^2+\psi'^2(t)\neq{0} ϕ′2+ψ′2(t)=0,则曲线积分 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds存在,且 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= ∫ α β [ f ( ϕ ( t ) , ψ ( t ) ) ] ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \int_{\alpha}^{\beta}[f(\phi(t),\psi(t))]\sqrt{\phi'^2(t)+\psi'^{2}(t)}\mathrm{d}t ∫αβ[f(ϕ(t),ψ(t))]ϕ′2(t)+ψ′2(t)dt, ( α < β ) (\alpha<\beta) (α<β)
(11)
- 若 ϕ ( t ) , ψ ( t ) \phi(t),\psi(t) ϕ(t),ψ(t)在 [ α , β ] [\alpha,\beta] [α,β]上具有一阶连续导数,且 ϕ ′ 2 + ψ ′ 2 ( t ) ≠ 0 \phi'^2+\psi'^2(t)\neq{0} ϕ′2+ψ′2(t)=0,则曲线积分 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds存在,且 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= ∫ α β [ f ( ϕ ( t ) , ψ ( t ) ) ] ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \int_{\alpha}^{\beta}[f(\phi(t),\psi(t))]\sqrt{\phi'^2(t)+\psi'^{2}(t)}\mathrm{d}t ∫αβ[f(ϕ(t),ψ(t))]ϕ′2(t)+ψ′2(t)dt, ( α < β ) (\alpha<\beta) (α<β)
证明(部分推导)
-
利用弧长公式,我们可以将第一类曲线积分化为定积分计算
- 弧长公式我们在定积分的应用中讨论过, s s s= ∫ α β ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \int_{\alpha}^{\beta}\sqrt{\phi'^2(t)+\psi'^2(t)}\mathrm{d}t ∫αβϕ′2(t)+ψ′2(t)dt
(12) - 令 r ( t ) = ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) r(t)=\sqrt{\phi'^{2}(t)+\psi'^{2}(t)} r(t)=ϕ′2(t)+ψ′2(t)
(12-1)
- 弧长公式我们在定积分的应用中讨论过, s s s= ∫ α β ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \int_{\alpha}^{\beta}\sqrt{\phi'^2(t)+\psi'^2(t)}\mathrm{d}t ∫αβϕ′2(t)+ψ′2(t)dt
-
假定当参数 t t t由 α \alpha α变至 β \beta β时,曲线弧 L L L上的点 M ( x , y ) M(x,y) M(x,y)依点 A A A运动至 B B B,该过程描出曲线弧 L L L
-
在 L L L上取一列点: A = M 0 , M 1 , ⋯ , M n = B A=M_0,M_1,\cdots,M_{n}=B A=M0,M1,⋯,Mn=B
-
设它们对应于一列单调增加的参数值 α = t 0 < t 1 < ⋯ < t n = β \alpha=t_0<t_1<\cdots<t_{n}=\beta α=t0<t1<⋯<tn=β(这表明 ( α < β ) (\alpha<\beta) (α<β))
-
根据对弧长的曲线积分的定义: ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= lim λ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \lim\limits_{\lambda\to{0}} \sum_{i=1}^{n}f(\xi_i,\eta_i)\Delta{s_i} λ→0lim∑i=1nf(ξi,ηi)Δsi(即式(3))
- 设点 ( ξ i , η i ) (\xi_i,\eta_i) (ξi,ηi)对应于参数值 τ i \tau_{i} τi,即 ξ i = ϕ ( τ i ) \xi_{i}=\phi(\tau_i) ξi=ϕ(τi), η i = ϕ ( τ i ) \eta_{i}=\phi(\tau_i) ηi=ϕ(τi)
(13),这里 τ i ∈ [ t i − 1 , t i ] \tau_{i}\in[t_{i-1},t_{i}] τi∈[ti−1,ti], - 记 t i − 1 → t i t_{i-1}\to{t_{i}} ti−1→ti在 L L L上对应的弧长为 Δ s i \Delta{s}_{i} Δsi,使用弧长公式(12),有 Δ s i \Delta{s_{i}} Δsi= ∫ t i − 1 t i ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) d t \int_{t_{i-1}}^{t_{i}}\sqrt{\phi'^2(t)+\psi'^2(t)}\mathrm{d}t ∫ti−1tiϕ′2(t)+ψ′2(t)dt
(14) - 由积分中值定理: Δ s i \Delta{s}_{i} Δsi= ϕ ′ 2 ( τ i ′ ) + ψ ′ 2 ( τ i ′ ) ⋅ Δ t i \sqrt{\phi'^2(\tau_{i}')+\psi'^2(\tau_{i}')}\cdot {\Delta{t_{i}}} ϕ′2(τi′)+ψ′2(τi′)⋅Δti
(15);其中 Δ t i \Delta{t_{i}} Δti= t i − t i − 1 t_{i}-t_{i-1} ti−ti−1, τ i ′ ∈ [ t i − 1 , t i ] \tau_{i}'\in[t_{i-1},t_{i}] τi′∈[ti−1,ti]于是 - Note:这里 τ i , τ i ′ \tau_i,\tau_i' τi,τi′有联系(都是 [ t i − 1 , t i ] [t_{i-1},t_{i}] [ti−1,ti]区间上的点),但并不相同
- 将式(13),(15)代入到式(3),于是 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= lim λ → 0 ∑ i = 1 n f [ ϕ ( τ i ) , ψ ( τ i ) ] ϕ ′ 2 ( τ i ′ ) + ψ ′ 2 ( τ i ′ ) Δ t i \lim\limits_{\lambda\to{0}}\sum_{i=1}^{n}f[\phi(\tau_{i}),\psi(\tau_{i})]\sqrt{\phi'^{2}(\tau_{i}')+\psi'^{2}(\tau_{i}')}\Delta{t_{i}} λ→0lim∑i=1nf[ϕ(τi),ψ(τi)]ϕ′2(τi′)+ψ′2(τi′)Δti
(16) - 由于函数(12-1)在闭区间 [ α , β ] [\alpha,\beta] [α,β]上连续,可以把上式中 r i ′ r_{i}' ri′替换为 r i r_{i} ri,从而式(16)写作式(11)
- 这一步要用到(12-1)函数在 [ α , β ] [\alpha,\beta] [α,β]上的一致连续性
- 设点 ( ξ i , η i ) (\xi_i,\eta_i) (ξi,ηi)对应于参数值 τ i \tau_{i} τi,即 ξ i = ϕ ( τ i ) \xi_{i}=\phi(\tau_i) ξi=ϕ(τi), η i = ϕ ( τ i ) \eta_{i}=\phi(\tau_i) ηi=ϕ(τi)
-
式(11)等号右端是一个定积分式子,因为其被积函数在 [ α , β ] [\alpha,\beta] [α,β]上连续,所以这个定积分是存在的,因此式(11)等号左端 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds也存在;并且可以有式(11)计算结果
小结
- 公式(11)表明,计算对弧长的曲线积分 f L f ( x , y ) d s f_{L}f(x,y)\mathrm{d}s fLf(x,y)ds时,只要将 x , y , d s x,y,\mathrm{d}s x,y,ds分别替换为: ϕ ( t ) , ψ ( t ) , ϕ ′ 2 t ) + ψ ′ 2 ( t ) d t \phi(t),\psi(t),\sqrt{\phi'^2{t)+\psi'^2(t)}}\mathrm{d}t ϕ(t),ψ(t),ϕ′2t)+ψ′2(t)dt
- 然后做 [ α , β ] [\alpha,\beta] [α,β]上的定积分即可 ( α < β ) (\alpha<\beta) (α<β)
曲线弧显函数形式方程下的曲线积分公式
- 若曲线弧 L L L由方程 y = ψ ( x ) y=\psi(x) y=ψ(x)
(17), ( x ∈ [ x 0 , X ] ) (x\in[x_0,X]) (x∈[x0,X])给出,则可以把这种情况看作特殊的参数方程:(参数方程的简单情形)- x = t x=t x=t, y = ψ ( t ) y=\psi(t) y=ψ(t), t ∈ [ x 0 , X ] t\in[x_{0},X] t∈[x0,X]
(17-1)
- x = t x=t x=t, y = ψ ( t ) y=\psi(t) y=ψ(t), t ∈ [ x 0 , X ] t\in[x_{0},X] t∈[x0,X]
- 将其代入公式(11),得 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= ∫ x 0 X f ( x , ψ ( x ) ) 1 + ψ ′ 2 ( x ) d x \int_{x_0}^{X}f(x,\psi(x)) \sqrt{1+\psi'^{2}(x)}\mathrm{d}x ∫x0Xf(x,ψ(x))1+ψ′2(x)dx, ( x 0 < X ) (x_0<X) (x0<X)
(18) - 类似地,若曲线弧 L L L由方程 x = ϕ ( y ) x=\phi(y) x=ϕ(y)
(19), ( y ∈ [ y 0 , Y ] ) (y\in[y_0,Y]) (y∈[y0,Y])给出- y = t y=t y=t, x = ϕ ( t ) x=\phi(t) x=ϕ(t)
(19-1), ( y ∈ [ y 0 , Y ] ) (y\in[y_0,Y]) (y∈[y0,Y])
- y = t y=t y=t, x = ϕ ( t ) x=\phi(t) x=ϕ(t)
- 则 ∫ L f ( x , y ) d s \int_{L}f(x,y)\mathrm{d}s ∫Lf(x,y)ds= ∫ y 0 Y f ( ϕ ( y ) , y ) 1 + ϕ ′ 2 ( y ) d y \int_{y_0}^{Y}f(\phi(y),y) \sqrt{1+\phi'^{2}(y)}\mathrm{d}y ∫y0Yf(ϕ(y),y)1+ϕ′2(y)dy, y 0 < Y y_{0}<Y y0<Y
(20)
推广
- 若空间曲线 Γ \Gamma Γ由参数方程 x = ϕ ( t ) x=\phi(t) x=ϕ(t), y = ψ ( t ) y=\psi(t) y=ψ(t), z = ω t z=\omega{t} z=ωt, t ∈ [ α , β ] t\in[\alpha,\beta] t∈[α,β]给出的情形,这时 f L f ( x , y , z ) d s f_{L}f(x,y,z)\mathrm{d}s fLf(x,y,z)ds= ∫ α β [ f ( ϕ ( t ) , ψ ( t ) , ω ( t ) ) ] ϕ ′ 2 ( t ) + ψ ′ 2 ( t ) + ω ′ 2 ( t ) d t \int_{\alpha}^{\beta}[f(\phi(t),\psi(t),\omega(t))]\sqrt{\phi'^2(t)+\psi'^{2}(t)+\omega'^{2}(t)}\mathrm{d}t ∫αβ[f(ϕ(t),ψ(t),ω(t))]ϕ′2(t)+ψ′2(t)+ω′2(t)dt ( α < β ) (\alpha<\beta) (α<β)
例
- 计算 ∫ L y d s \int_{L}\sqrt{y}\mathrm{d}s ∫Lyds其中 L L L时抛物线 y = x 2 y=x^2 y=x2上点 O ( 0 , 0 ) O(0,0) O(0,0)与 B ( 1 , 1 ) B(1,1) B(1,1)之间的一段弧
- 曲线 L L L表示为 x x x为参数的参数方程: y = x 2 y=x^2 y=x2, x ∈ [ 0 , 1 ] x\in[0,1] x∈[0,1]
- ∫ L y d s \int_{L}\sqrt{y}\mathrm{d}s ∫Lyds= ∫ 0 1 x 2 1 + ( x 2 ) ′ 2 d x \int_{0}^{1}\sqrt{x^2}\sqrt{1+(x^2)'^2}\mathrm{d}x ∫01x21+(x2)′2dx= ∫ 0 1 x 1 + 4 x 2 d x \int_{0}^{1}x\sqrt{1+4x^2}\mathrm{d}x ∫01x1+4x2dx
- 第一换元法: 1 2 ∫ 0 1 1 + 4 x 2 d x 2 \frac{1}{2}\int_{0}^{1}\sqrt{1+4x^2}\mathrm{d}x^2 21∫011+4x2dx2= 1 8 ∫ 0 1 1 + 4 x 2 d ( 4 x 2 + 1 ) \frac{1}{8}\int_{0}^{1}\sqrt{1+4x^2}\mathrm{d}(4x^2+1) 81∫011+4x2d(4x2+1)= 1 8 2 3 ( 1 + 4 x 2 ) 3 2 ∣ 0 1 \frac{1}{8}\frac{2}{3}(1+4x^2)^{\frac{3}{2}}|_{0}^{1} 8132(1+4x2)23∣01= 1 12 [ ( 1 + 4 ) 3 2 − 1 ] \frac{1}{12}[(1+4)^{\frac{3}{2}}-1] 121[(1+4)23−1]= 1 12 ( 5 5 − 1 ) \frac{1}{12}(5\sqrt{5}-1) 121(55−1)
例
-
若 L L L: x = R cos θ x=R\cos\theta x=Rcosθ, y = R sin θ y=R\sin\theta y=Rsinθ, θ ∈ [ − α , α ] \theta\in[-\alpha,\alpha] θ∈[−α,α]
-
I I I= ∫ L y 2 d s \int_{L}y^2\mathrm{d}s ∫Ly2ds= ∫ − α α R 2 sin 2 θ ( − R sin θ ) 2 + ( R cos θ ) 2 d θ \int_{-\alpha}^{\alpha}R^2\sin^2\theta\sqrt{(-R\sin\theta)^2+(R\cos\theta)^2}\mathrm{d}\theta ∫−ααR2sin2θ(−Rsinθ)2+(Rcosθ)2dθ
- = R 3 ∫ − a a sin 2 θ d θ R^3\int_{-a}^{a}\sin^2\theta\mathrm{d}\theta R3∫−aasin2θdθ= R 3 2 [ θ − sin 2 θ 2 ] − α α \frac{R^3}{2}[\theta-\frac{\sin 2\theta}{2}]_{-\alpha}^{\alpha} 2R3[θ−2sin2θ]−αα= R 3 2 ( 2 α − sin 2 α ) \frac{R^3}{2}(2\alpha-\sin2\alpha) 2R3(2α−sin2α)= R 3 ( α − sin α cos α ) R^3(\alpha-\sin\alpha\cos\alpha) R3(α−sinαcosα)
例
- 若 L L L: x = a cos t x=a\cos{t} x=acost, y = a sin t y=a\sin{t} y=asint, z = k t z=kt z=kt, t ∈ [ 0 , 2 π ] t\in[0,2\pi] t∈[0,2π],求 I I I= ∫ Γ ( x 2 + y 2 + z 2 ) d s \int_{\Gamma}(x^2+y^2+z^2)\mathrm{d}s ∫Γ(x2+y2+z2)ds
- I I I= ∫ Γ ( a 2 cos 2 t + a 2 sin 2 t + k 2 t 2 ) ( − a sin t ) 2 + ( a cos t ) 2 + k 2 d t \int_{\Gamma}(a^2\cos^2{t}+a^2\sin^2t+k^2t^2)\sqrt{(-a\sin{t})^2+(a\cos{t})^2+k^2}\mathrm{d}t ∫Γ(a2cos2t+a2sin2t+k2t2)(−asint)2+(acost)2+k2dt
- = ∫ 0 2 π ( a 2 + k 2 t 2 ) a 2 + k 2 d t \int_{0}^{2\pi}(a^2+k^2t^2)\sqrt{a^2+k^2}\mathrm{d}t ∫02π(a2+k2t2)a2+k2dt= a 2 + k 2 [ a 2 t + k 2 3 t 3 ] 0 2 π \sqrt{a^2+k^2}[a^2t+\frac{k^2}{3}t^3]_{0}^{2\pi} a2+k2[a2t+3k2t3]02π
- 提取与 t t t无关的因式 a 2 + k 2 \sqrt{a^2+k^2} a2+k2到积分号前
- = a 2 + k 2 [ 2 a 2 π + 8 3 k 2 π 2 ] \sqrt{a^2+k^2}[2a^2\pi+\frac{8}{3}k^2\pi^2] a2+k2[2a2π+38k2π2]
- = 2 π 3 a 2 + k 2 ( 3 a 2 + 4 π 2 k 2 ) \frac{2\pi}{3}\sqrt{a^2+k^2}(3a^2+4\pi^2k^2) 32πa2+k2(3a2+4π2k2)
相关文章:

第一类曲线积分@对弧长的曲线积分
文章目录 abstract对弧长的曲线积分曲线形构件的质量第一类曲线积分曲线积分存在性利用曲线积分的定义描述曲线形构件质量问题推广曲线积分可加性闭曲线积分 曲线积分性质曲线积分的计算方法证明(部分推导) 小结曲线弧显函数形式方程下的曲线积分公式推广例例例 abstract 在积…...
【TypeScript】常见数据结构与算法(二):链表
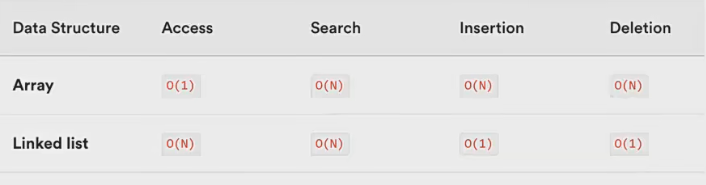
文章目录 链表结构(LinkedList)链表以及数组的缺点数组链表的优势 什么是链表?封装链表相关方法源码链表常见面试题237-删除链表中的节点206 - 反转链表 数组和链表的复杂度对比 链表结构(LinkedList) 链表以及数组的缺点 链表…...
)
原型模式 (Prototype Pattern)
定义: 原型模式(Prototype Pattern)是一种创建型设计模式,它用于创建重复的对象,同时保持性能。这种模式的核心思想是通过复制一个已存在的实例来创建新的实例,而不是新建实例并对其进行初始化。原型模式适…...

项目总结报告(案例模板)
软件项目总结报告模板套用: 项目概要项目工作分析经验与教训改进建议可纳入的项目过程资产 --------进主页获取更多资料-------...

C++ Qt QByteArray用法介绍
作者:令狐掌门 技术交流QQ群:675120140 csdn博客:https://mingshiqiang.blog.csdn.net/ 文章目录 一、QByteArray的基本用法1、初始化和赋值2、访问和修改元素3、 常用方法4、数据转换二、QByteArray与文件操作三、QByteArray与网络编程四、QByteArray数据编码1、Base64 编解…...
蓝桥杯物联网竞赛_STM32L071_3_Oled显示
地位: 对于任何一门编程语言的学习,print函数毫无疑问是一种最好的调试手段,调试者不仅能通过它获取程序变量的运行状态而且通过对其合理使用获取程序的运行流程,更能通过关键变量的输出帮你验证推理的正确与否,朴素的…...
python-opencv轮廓检测(外轮廓检测和全部轮廓检测,计算轮廓面积和周长)
python-opencv轮廓检测(外轮廓检测和全部轮廓检测,计算轮廓面积和周长) 通过cv2.findContours,我们可以进行轮廓检测,当然也有很多检测模式,我们可以通过选择检测模式,进行外轮廓检测ÿ…...

LeetCode [简单] 1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以按任意顺序返回…...
C++设计模式之工厂模式(下)——抽象工厂模式
抽象工厂模式 介绍示例示例使用运行结果抽象工厂模式的优缺点优点缺点 总结 介绍 抽象工厂模式是一种创建型设计模式,它提供了一种封装一组相关或相互依赖对象的方式,而无需指定它们具体的类。它允许客户端使用抽象接口来创建一系列相关的对象ÿ…...
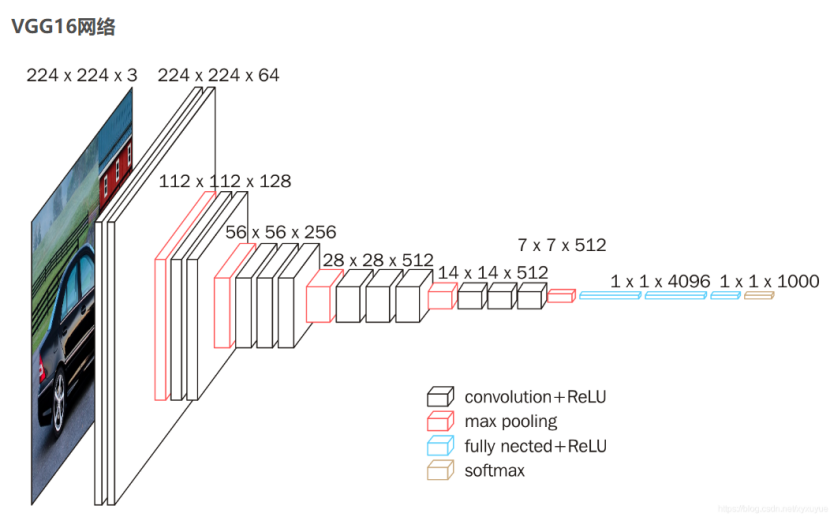
2023亚太杯数学建模A题思路分析 - 采果机器人的图像识别技术
1 赛题 问题A 采果机器人的图像识别技术 中国是世界上最大的苹果生产国,年产量约为3500万吨。与此同时,中国也是世 界上最大的苹果出口国,全球每两个苹果中就有一个,全球超过六分之一的苹果出口 自中国。中国提出了一带一路倡议…...

关于Flink的旁路缓存与异步操作
1. 旁路缓存 1. 什么是旁路缓存? 将数据库中的数据,比较经常访问的数据,保存起来,以减少和硬盘数据库的交互 比如: 我们使用mysql时 经常查询一个表 , 而这个表又一般不会变化,就可以放在内存中,查找时直接对内存进行查找,而不需要再和mysql交互 2. 旁路缓存例子使用 dim层…...

MyBatis-Plus的分页插件和乐观锁插件
MyBatis-Plus: 探索分页查询和乐观锁插件 在现代的Web应用开发中,高效的数据处理是不可或缺的一部分。MyBatis-Plus,作为MyBatis的增强版,提供了多种插件来简化和优化数据库操作。在这篇博客中,我们将重点介绍两个非常实用的插件…...
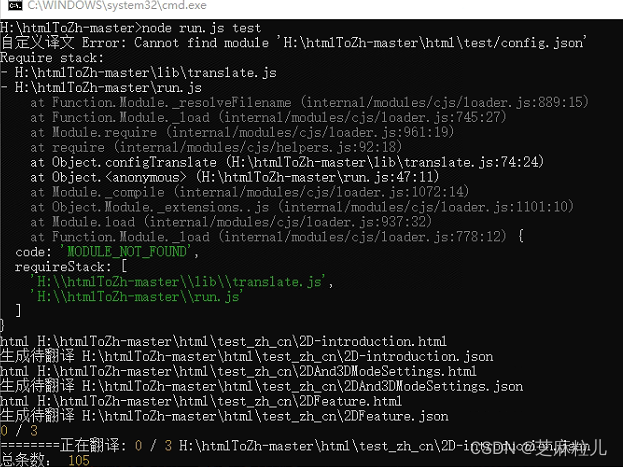
批量将本地N个英文Html文档进行中文翻译-操作篇
Unity3D特效百例案例项目实战源码Android-Unity实战问题汇总游戏脚本-辅助自动化Android控件全解手册再战Android系列Scratch编程案例软考全系列Unity3D学习专栏蓝桥系列ChatGPT和AIGC 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分…...
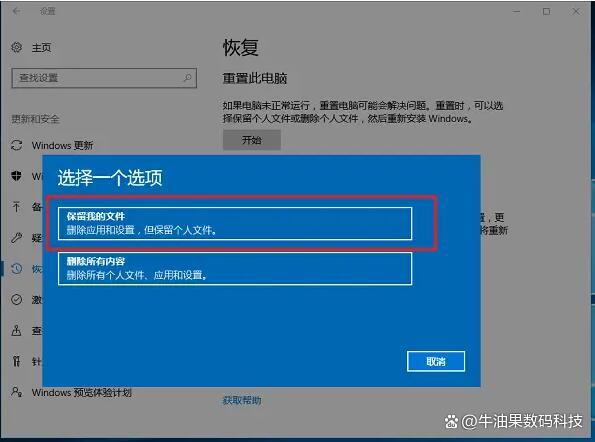
解决cad找不到vcruntime140.dll的方法,实测有效的5个的方法
最近,我在使用CAD软件时遇到了一个困扰我已久的问题:由于找不到vcruntime140.dll文件而导致CAD无法正常运行。经过一番努力和尝试,我终于找到了解决这个问题的方法。那么,如何解决vcruntime140.dll丢失的问题呢?本文将…...

2023亚太杯数学建模C题:我国新能源电动汽车的发展趋势,思路模型代码
问题C 我国新能源电动汽车的发展趋势 赛题思路:获取思路见文末名片,第一时间更新 新能源汽车是指以先进技术原理、新技术、新结构的非常规汽车燃料为动力来源( 非常规汽车燃料指汽油、柴油以外的燃料),将先进技术进行汽车动力控制…...

英语学习-爆破音
英文爆破音有:[p],[b],[t],[d],[k],[g]。 同时爆破音的发音会根据前后音的不同,发音不同,具体如下: ⒈ [p],[b],[t],[d],[k],[g] 中的任何两个音素相邻时,前面的发不完全爆破音,后面的就要完全地爆破。如…...

【Vue】图片切换
上一篇: vue的指令 https://blog.csdn.net/m0_67930426/article/details/134599378?spm1001.2014.3001.5502 本篇所需要的指令有: v-on v-bind v-show <!DOCTYPE html> <html lang"en"> <head><meta charset"…...

C++模拟如何实现vector的方法
任意位置插入,insert的返回值为新插入的第一个元素位置的迭代器;因为插入可能会进行扩容,导致start的值改变,所以先定义一个变量保存pos与start的相对位置;判断是否需要扩容;从插入位置开始,将所…...

芯知识 | 混音播报语音芯片的优势:革新音频应用的新力量
随着科技的进步,语音芯片在各个领域的应用越来越广泛。而在众多语音芯片中,混音播报语音芯片以其独特的优势,正逐渐成为音频应用领域的翘楚。本文将重点探讨混音播报语音芯片的优势及其在现代科技应用中的价值。 一、混音播报语音芯片概述 …...
)
Arduino驱动PT100数字K型高温传感器(温湿度传感器)
目录 1、传感器特性 2、控制器和传感器连线图 3、硬件原理图 4、驱动程序 PT100适用于大部分400℃以下高温的测量,但是通常家用天然气灶焰芯温度可达800℃以上,烧制陶瓷的窖子或者大功率电炉温度更可超过1000℃,在这些超高温度的场景下就需要用到K型热电偶。...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
