【机器学习】聚类(一):原型聚类:K-means聚类
文章目录
- 一、实验介绍
- 1. 算法流程
- 2. 算法解释
- 3. 算法特点
- 4. 应用场景
- 5. 注意事项
- 二、实验环境
- 1. 配置虚拟环境
- 2. 库版本介绍
- 三、实验内容
- 0. 导入必要的库
- 1. Kmeans类
- a. 构造函数
- b. 闵可夫斯基距离
- c. 初始化簇心
- d. K-means聚类
- e. 聚类结果可视化
- 2. 辅助函数
- 3. 主函数
- a. 命令行界面 (CLI)
- b. 数据加载
- c. 模型训练及可视化
- 4. 运行脚本的命令
- 5. 代码整合
原型聚类中的K均值算法是一种常用的聚类方法,该算法的目标是通过迭代过程找到数据集的簇划分,使得每个簇内的样本与簇内均值的平方误差最小化。这一过程通过不断迭代更新簇的均值来实现。
一、实验介绍

1. 算法流程
- 初始化: 从样本集中随机选择k个样本作为初始均值向量。
- 迭代过程: 重复以下步骤直至均值向量不再更新:
- 对每个样本计算与各均值向量的距离。
- 将样本划分到距离最近的均值向量所对应的簇。
- 更新每个簇的均值向量为该簇内样本的平均值。
- 输出: 返回最终的簇划分。
2. 算法解释
- 步骤1中,通过随机选择初始化k个均值向量。
- 步骤2中,通过计算样本与均值向量的距离,将每个样本分配到最近的簇。然后,更新每个簇的均值向量为该簇内样本的平均值。
- 算法通过迭代更新,不断优化簇内样本与均值向量的相似度,最终得到较好的聚类结果。
3. 算法特点
- K均值算法是一种贪心算法,通过局部最优解逐步逼近全局最优解。
- 由于需要对每个样本与均值向量的距离进行计算,算法复杂度较高。
- 对于大型数据集和高维数据,K均值算法的效果可能受到影响。
4. 应用场景
- K均值算法适用于样本集可以被均值向量较好表示的情况,特别是当簇呈现球形或近似球形分布时效果较好。
- 在图像分割、用户行为分析等领域广泛应用。
5. 注意事项
- 对于K均值算法,初始均值向量的选择可能影响最终聚类结果,因此有时需要多次运行算法,选择最优的结果。
- 算法对异常值敏感,可能导致簇的均值向量被拉向异常值,因此在处理异常值时需要谨慎。
二、实验环境
1. 配置虚拟环境
conda create -n ML python==3.9
conda activate ML
conda install scikit-learn matplotlib seaborn
2. 库版本介绍
| 软件包 | 本实验版本 |
|---|---|
| matplotlib | 3.5.2 |
| numpy | 1.21.5 |
| python | 3.9.13 |
| scikit-learn | 1.0.2 |
| seaborn | 0.11.2 |
三、实验内容
0. 导入必要的库
import numpy as np
import random
import seaborn as sns
import matplotlib.pyplot as plt
import argparse
1. Kmeans类
__init__:初始化K均值聚类的参数,包括聚类数目k、数据data、初始化模式mode(默认为 “random”)、最大迭代次数max_iters、闵可夫斯基距离的阶数p、随机种子seed等。minkowski_distance函数:计算两个样本点之间的闵可夫斯基距离。center_init函数:根据指定的模式初始化聚类中心。fit方法:执行K均值聚类的迭代过程,包括分配样本到最近的簇、更新簇中心,直到满足停止条件。visualization函数:使用Seaborn和Matplotlib可视化聚类结果。
a. 构造函数
class Kmeans(object):def __init__(self, k, data: np.ndarray, mode="random", max_iters=0, p=2, seed=0):self.k = kself.data = dataself.mode = modeself.max_iter = max_iters if max_iters > 0 else int(1e8)self.p = pself.seed = seedself.centers = Noneself.clu_idx = np.zeros(len(self.data), dtype=np.int32) # 样本的分类簇self.clu_dist = np.zeros(len(self.data), dtype=np.float64) # 样本与簇心的距离
- 参数:
- 聚类数目
k - 数据集
data - 初始化模式
mode - 最大迭代次数
max_iters - 闵可夫斯基距离的阶数
p以及随机种子seed。
- 聚类数目
- 初始化类的上述属性,此外
self.centers被初始化为None,表示簇心尚未计算self.clu_idx和self.clu_dist被初始化为全零数组,表示每个样本的分类簇和与簇心的距离。
b. 闵可夫斯基距离
def minkowski_distance(self, x, y=0):return np.linalg.norm(x - y, ord=self.p)
- 使用了NumPy的
linalg.norm函数,其中ord参数用于指定距离的阶数。
c. 初始化簇心
def center_init(self):random.seed(self.seed)if self.mode == "random":ids = random.sample(range(len(self.data)), k=self.k) # 随机抽取k个样本下标self.centers = self.data[ids] # 选取k个样本作为簇中心else:ids = [random.randint(0, self.data.shape[0])]for _ in range(1, self.k):max_idx = 0max_dis = 0for i, x in enumerate(self.data):if i in ids:continuedis = 0for y in self.data[ids]:dis += self.minkowski_distance(x - y)if max_dis < dis:max_dis = dismax_idx = iids.append(max_idx)self.centers = self.data[ids]
- 根据指定的初始化模式,选择随机样本或使用 “far” 模式。
- 在 “random” 模式下,通过随机抽样选择
k个样本作为簇心; - 在 “far” 模式下,通过计算每个样本到已选簇心的距离之和,选择距离总和最大的样本作为下一个簇心。
- 在 “random” 模式下,通过随机抽样选择
d. K-means聚类
def fit(self):self.center_init() # 簇心初始化for _ in range(self.max_iter):flag = False # 判断是否有样本被重新分类# 遍历每个样本for i, x in enumerate(self.data):min_idx = -1 # 最近簇心下标min_dist = np.inf # 最小距离for j, y in enumerate(self.centers): # 遍历每个簇,计算与该样本的距离# 计算样本i到簇j的距离distdist = self.minkowski_distance(x, y)if min_dist > dist:min_dist = distmin_idx = jif self.clu_idx[i] != min_idx:# 有样本改变分类簇,需要继续迭代更新簇心flag = True# 记录样本i与簇的最小距离min_dist,及对应簇的下标min_idxself.clu_idx[i] = min_idxself.clu_dist[i] = min_dist# 样本的簇划分好之后,用样本均值更新簇心for i in range(self.k):x = self.data[self.clu_idx == i]# 用样本均值更新簇心self.centers[i] = np.mean(x, axis=0)if not flag:break
- 在每次迭代中
- 遍历每个样本,计算其到各个簇心的距离,将样本分配到距离最近的簇中。
- 更新每个簇的均值(簇心)为该簇内所有样本的平均值。
- 上述过程迭代进行,直到满足停止条件(样本不再重新分配到不同的簇)或达到最大迭代次数。
e. 聚类结果可视化
def visualization(self, k=3):current_palette = sns.color_palette()sns.set_theme(context="talk", palette=current_palette)for i in range(self.k):x = self.data[self.clu_idx == i]sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8)sns.scatterplot(x=self.centers[:, 0], y=self.centers[:, 1], marker="+", s=500)plt.title("k=" + str(k))plt.show()
2. 辅助函数
def order_type(v: str):if v.lower() in ("-inf", "inf"):return -np.inf if v.startswith("-") else np.infelse:try:return float(v)except ValueError:raise argparse.ArgumentTypeError("Unsupported value encountered")def mode_type(v: str):if v.lower() in ("random", "far"):return v.lower()else:raise argparse.ArgumentTypeError("Unsupported value encountered")order_type函数:用于处理命令行参数中的-p(距离测量参数),将字符串转换为浮点数。mode_type函数:用于处理命令行参数中的--mode(初始化模式参数),将字符串转换为合法的初始化模式。
3. 主函数
a. 命令行界面 (CLI)
- 使用
argparse解析命令行参数
parser = argparse.ArgumentParser(description="Kmeans Demo")parser.add_argument("-k", type=int, default=3, help="The number of clusters")parser.add_argument("--mode", type=mode_type, default="random", help="Initial centroid selection")parser.add_argument("-m", "--max-iters", type=int, default=40, help="Maximum iterations")parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")parser.add_argument("--seed", type=int, default=0, help="Random seed")parser.add_argument("--dataset", type=str, default="./kmeans.2.txt", help="Path to dataset")args = parser.parse_args()b. 数据加载
- 从指定路径加载数据集。
dataset = np.loadtxt(args.dataset)
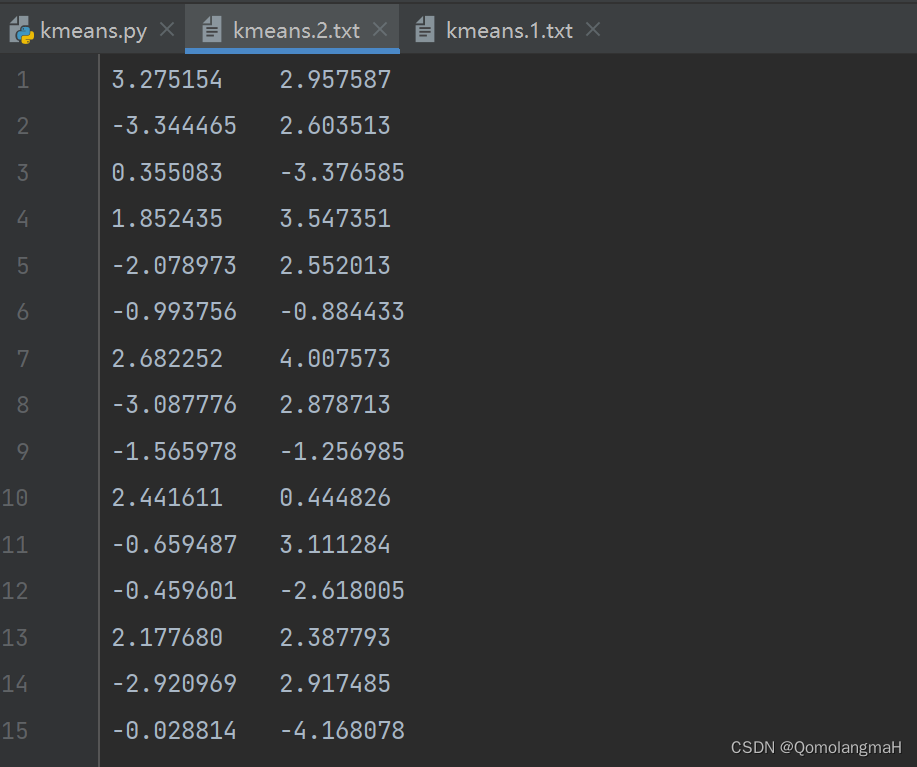
c. 模型训练及可视化
model = Kmeans(k=args.k, data=dataset, mode=args.mode, max_iters=args.max_iters, p=args.p,seed=args.seed)model.fit()# 聚类结果可视化model.visualization(k=args.k)
4. 运行脚本的命令
- 通过命令行传递参数来运行脚本,指定聚类数目、初始化模式、最大迭代次数等。
python kmeans.py -k 3 --mode random -m 40 -p 2 --seed 0 --dataset ./kmeans.2.txt
5. 代码整合
import numpy as np
import random
import seaborn as sns
import matplotlib.pyplot as plt
import argparseclass Kmeans(object):def __init__(self, k, data: np.ndarray, mode="random", max_iters=0, p=2, seed=0):self.k = kself.data = dataself.mode = modeself.max_iter = max_iters if max_iters > 0 else int(1e8)self.p = pself.seed = seedself.centers = Noneself.clu_idx = np.zeros(len(self.data), dtype=np.int32) # 样本的分类簇self.clu_dist = np.zeros(len(self.data), dtype=np.float64) # 样本与簇心的距离def minkowski_distance(self, x, y=0):return np.linalg.norm(x - y, ord=self.p)# 簇心初始化def center_init(self):random.seed(self.seed)if self.mode == "random":ids = random.sample(range(len(self.data)), k=self.k) # 随机抽取k个样本下标self.centers = self.data[ids] # 选取k个样本作为簇中心else:ids = [random.randint(0, self.data.shape[0])]for _ in range(1, self.k):max_idx = 0max_dis = 0for i, x in enumerate(self.data):if i in ids:continuedis = 0for y in self.data[ids]:dis += self.minkowski_distance(x - y)if max_dis < dis:max_dis = dismax_idx = iids.append(max_idx)self.centers = self.data[ids]def fit(self):self.center_init() # 簇心初始化for _ in range(self.max_iter):flag = False # 判断是否有样本被重新分类# 遍历每个样本for i, x in enumerate(self.data):min_idx = -1 # 最近簇心下标min_dist = np.inf # 最小距离for j, y in enumerate(self.centers): # 遍历每个簇,计算与该样本的距离# 计算样本i到簇j的距离distdist = self.minkowski_distance(x, y)if min_dist > dist:min_dist = distmin_idx = jif self.clu_idx[i] != min_idx:# 有样本改变分类簇,需要继续迭代更新簇心flag = True# 记录样本i与簇的最小距离min_dist,及对应簇的下标min_idxself.clu_idx[i] = min_idxself.clu_dist[i] = min_dist# 样本的簇划分好之后,用样本均值更新簇心for i in range(self.k):x = self.data[self.clu_idx == i]# 用样本均值更新簇心self.centers[i] = np.mean(x, axis=0)if not flag:breakdef visualization(self, k=3):current_palette = sns.color_palette()sns.set_theme(context="talk", palette=current_palette)for i in range(self.k):x = self.data[self.clu_idx == i]sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8)sns.scatterplot(x=self.centers[:, 0], y=self.centers[:, 1], marker="+", s=500)plt.title("k=" + str(k))plt.show()def order_type(v: str):if v.lower() in ("-inf", "inf"):return -np.inf if v.startswith("-") else np.infelse:try:return float(v)except ValueError:raise argparse.ArgumentTypeError("Unsupported value encountered")def mode_type(v: str):if v.lower() in ("random", "far"):return v.lower()else:raise argparse.ArgumentTypeError("Unsupported value encountered")if __name__ == '__main__':parser = argparse.ArgumentParser(description="Kmeans Demo")parser.add_argument("-k", type=int, default=3, help="The number of clusters")parser.add_argument("--mode", type=mode_type, default="random", help="Initial centroid selection")parser.add_argument("-m", "--max-iters", type=int, default=40, help="Maximum iterations")parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")parser.add_argument("--seed", type=int, default=0, help="Random seed")parser.add_argument("--dataset", type=str, default="./kmeans.2.txt", help="Path to dataset")args = parser.parse_args()dataset = np.loadtxt(args.dataset)model = Kmeans(k=args.k, data=dataset, mode=args.mode, max_iters=args.max_iters, p=args.p,seed=args.seed) # args.seed)model.fit()# 聚类结果可视化model.visualization(k=args.k)相关文章:

【机器学习】聚类(一):原型聚类:K-means聚类
文章目录 一、实验介绍1. 算法流程2. 算法解释3. 算法特点4. 应用场景5. 注意事项 二、实验环境1. 配置虚拟环境2. 库版本介绍 三、实验内容0. 导入必要的库1. Kmeans类a. 构造函数b. 闵可夫斯基距离c. 初始化簇心d. K-means聚类e. 聚类结果可视化 2. 辅助函数3. 主函数a. 命令…...

2824. 统计和小于目标的下标对数目 --力扣 --JAVA
题目 给你一个下标从 0 开始长度为 n 的整数数组 nums 和一个整数 target ,请你返回满足 0 < i < j < n 且 nums[i] nums[j] < target 的下标对 (i, j) 的数目。 解题思路 对数组进行排序,可以利用List自带的sort函数传递比较规则(代码中的…...
github上不去
想要网上找代码发现github上不去了 发现之前的fastgit也用不了了 搜了很多地方终于找到了 记录保存一下 fastgithub最新下载 选择第二个下载解压就行 使用成功!...

图像处理Scharr 算子
Scharr算子是用于图像边缘检测的一种算子,它类似于Sobel算子,但是对边缘的响应更加强烈。它可以用来检测图像中的边缘、轮廓等特征。 原理: Scharr算子是一种卷积核(也称为卷积模板),用于计算图像的梯度。…...

JAVA 面向对象编程
一. 类与对象 1.1 定义类 :类是由数据成员和成员方法组成的一个程序单元。数据成员表示类的属性,成员方法表示类的行为。 定义类的语法格式 : class 类名{数据类型 数据成员名;...public 返回值类型 方法名(参数 2, 参数 2 ...){// 方法体[return 表达…...
)
第十六章 解读深度学习中Batch Size、Iterations和Epochs(工具)
训练网络之前有很多参数要设置,不了解各个参数的含义就没法合理地设置参数值,训练效果也会因此大受影响。本篇博客记录一下网络训练里的Batch Size、Iterations和Epochs怎么理解。 一、引言 首先要了解一下为什么会出现Batch Size这个概念。深度学习算…...

基于UI交互意图理解的异常检测方法
美团到店平台技术部/质量工程部与复旦大学周扬帆教授团队开展了科研合作,基于业务实际场景,自主研发了多模态UI交互意图识别模型以及配套的UI交互框架。 本文从大前端质量保障领域的痛点出发,介绍了UI交互意图识别的方法设计与实现。基于UI交…...
ArgoWorkflow教程(一)---DevOps 另一选择?云原生 CICD: ArgoWorkflow 初体验
来自:探索云原生 https://www.lixueduan.com 原文:https://www.lixueduan.com/posts/devops/argo-workflow/01-deploy-argo-workflows/ 本文主要记录了如何在 k8s 上快速部署云原生的工作流引擎 ArgoWorkflow。 ArgoWorkflow 是什么 Argo Workflows 是…...
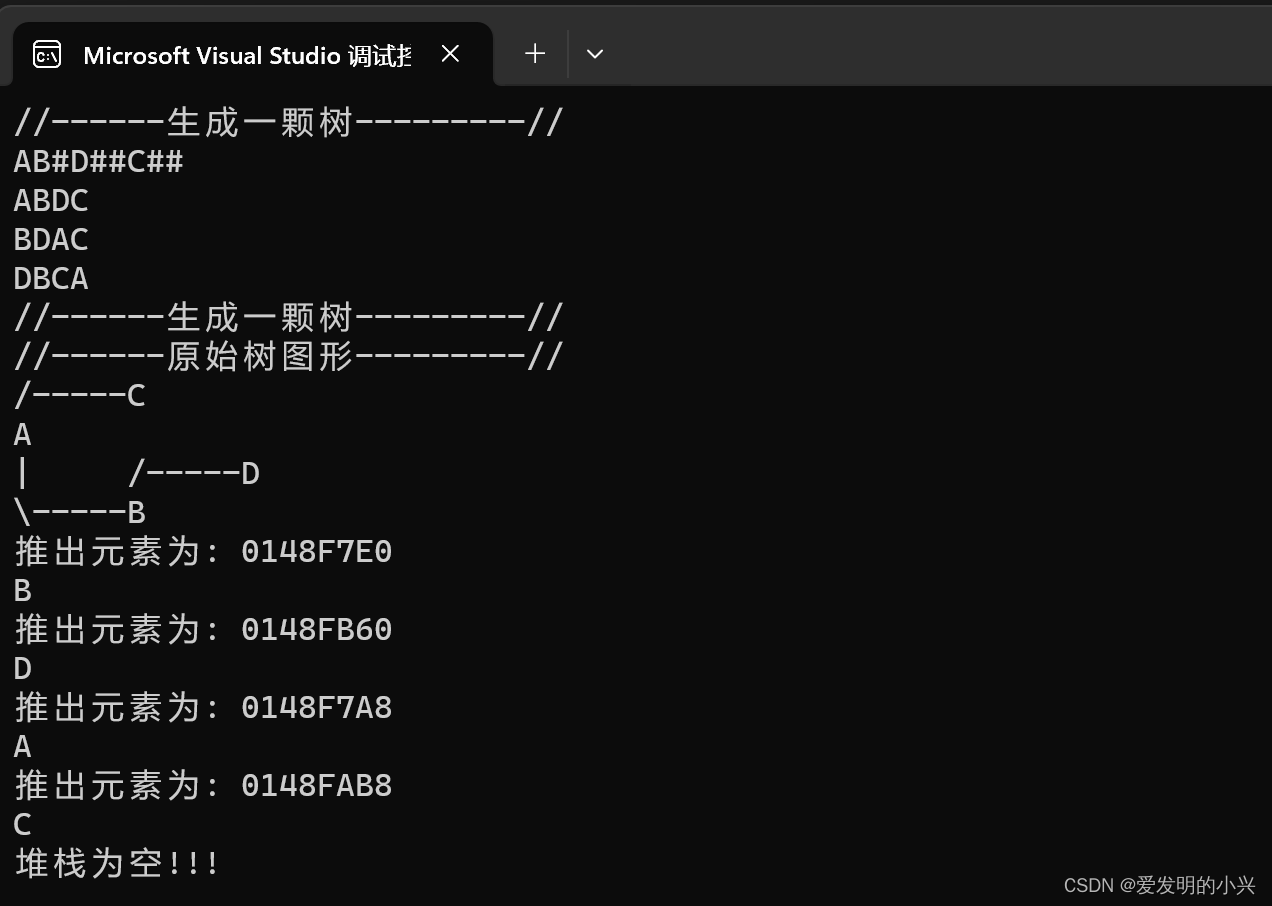
数据结构与算法编程题24
中序遍历非递归算法 #define _CRT_SECURE_NO_WARNINGS#include <iostream> using namespace std;typedef char ElemType; #define ERROR 0 #define OK 1 #define Maxsize 100 #define STR_SIZE 1024typedef struct BiTNode {ElemType data;BiTNode* lchild, * rchild; }B…...

springsecurity6配置四
一、springsecurity自定义过滤url配置 package com.school.information.config;import lombok.Data; import org.springframework.boot.context.properties.ConfigurationProperties; import org.springframework.stereotype.Component;import java.util.List;/*** 需要放行的…...
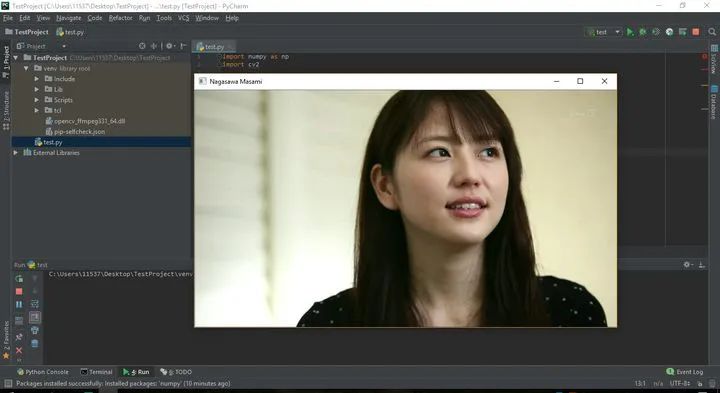
OpenCV简介及安装
前言 因为最近想做图像处理、人脸检测/识别之类的相关开发,所以就开始补OpenCV的相关知识,便开个专栏用于记录学习历程和在学习过程中遇到的一些值得注意的重点和坑。 学习过程基本上也是面向官方文档和Google。 简介 OpenCV(开源的计算机视觉库)是基于…...

Unity调用dll踩坑记
请用写一段代码,让unity无声无息的崩溃。 你说这怕是有点难哦,谁会这么不幸呢?不幸的是,我幸运的成为了那个不幸的人。 unity里面调用dll的方式是使用 DllImport ,比如有一个 Hello.dll,里面有一个 char* …...

Oracle 数据库基线安全加固操作
目录 账号管理、认证授权 ELK-Oracle-01-01-01 ELK-Oracle-01-01-02 ELK-Oracle-01-01-03 ELK-Oracle-01-01-04 ELK-Oracle-01-01-05 ELK-Oracle-01-01-06 ELK-Oracle-01-01-07 …...
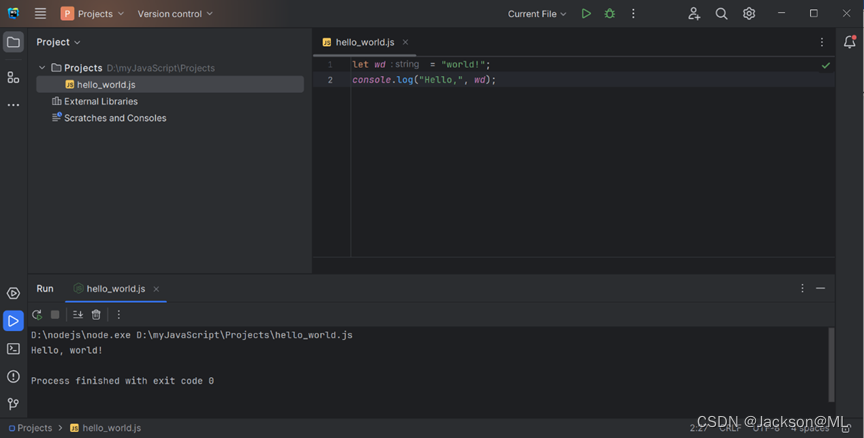
安装最新版WebStorm来开发JavaScript应用程序
安装最新版WebStorm来开发JavaScript应用程序 Install the Latest Version of JetBrains WebStorm to Develop JavaScript Applications By JacksonML 2023-11-25 1. 系统要求 WebStorm是个跨平台集成开发环境(IDE)。按照JetBrains官网对WebStorm软件…...

python opencv 放射变换和图像缩放-实现图像平移旋转缩放
python opencv 放射变换和图像缩放-实现图像平移旋转缩放 我们实现这次实验主要用到cv2.resize和cv2.warpAffine cv2.warpAffine主要是传入一个图像矩阵,一个M矩阵,输出一个dst结果矩阵,计算公式如下: cv2.resize则主要使用fx&…...
库与PyCharm】)
安装Anaconda、PyTorch(GPU版)库与PyCharm】
【Python深度学习:安装Anaconda、PyTorch(GPU版)库与PyCharm】https://www.bilibili.com/video/BV1cD4y1H7Tk?vd_source0aeb782d0b9c2e6b0e0cdea3e2121ebadownload.pytorch.org/whl/torchaudio/更改Jupyter Notebook的默认路径,亲…...
关于pytorch以及相关包的安装教程
一.查看自己电脑的配置 首先查看自己电脑的cuda的版本,WinR,敲入cmd打开终端 输入nvidia-smi,查看自己电脑的显卡等配置 这里要说明一下关于这个CUDA,它具有向后兼容性,这意味着支持较低版本的 CUDA 的应用程序通常也可以在较高版本的 CUD…...
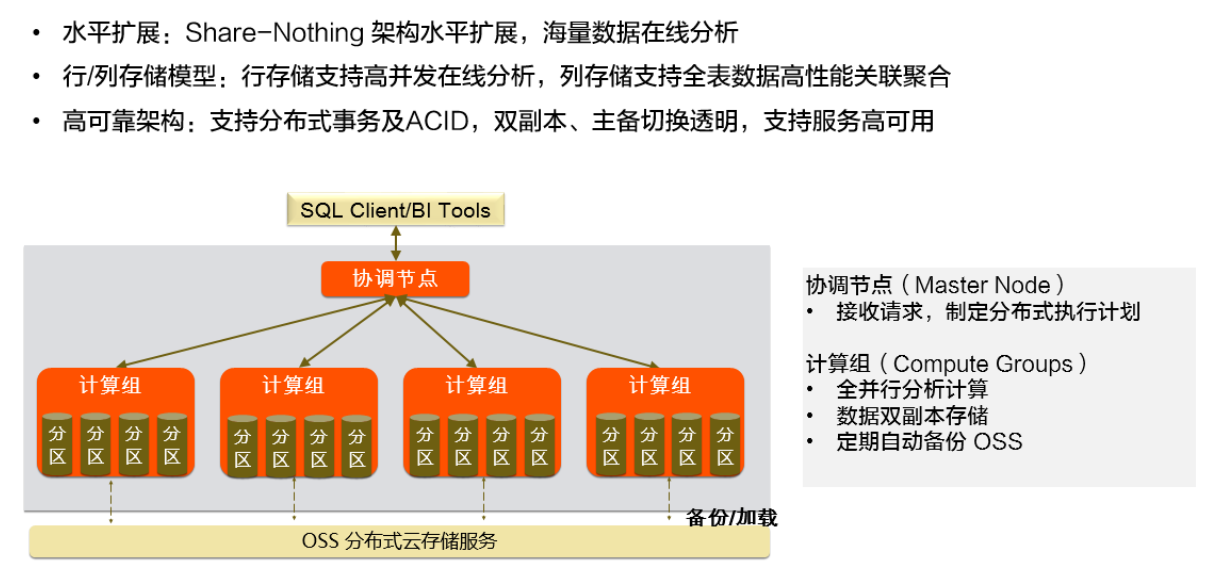
AnalyticDB for PostgreSQL 实时数据仓库上手指南
AnalyticDB for PostgreSQL 实时数据仓库上手指南 2019-04-016601 版权 本文涉及的产品 云原生数据仓库 ADB PostgreSQL,4核16G 50GB 1个月 推荐场景: 构建的企业专属Chatbot 立即试用 简介: AnalyticDB for PostgreSQL 提供企业级数…...
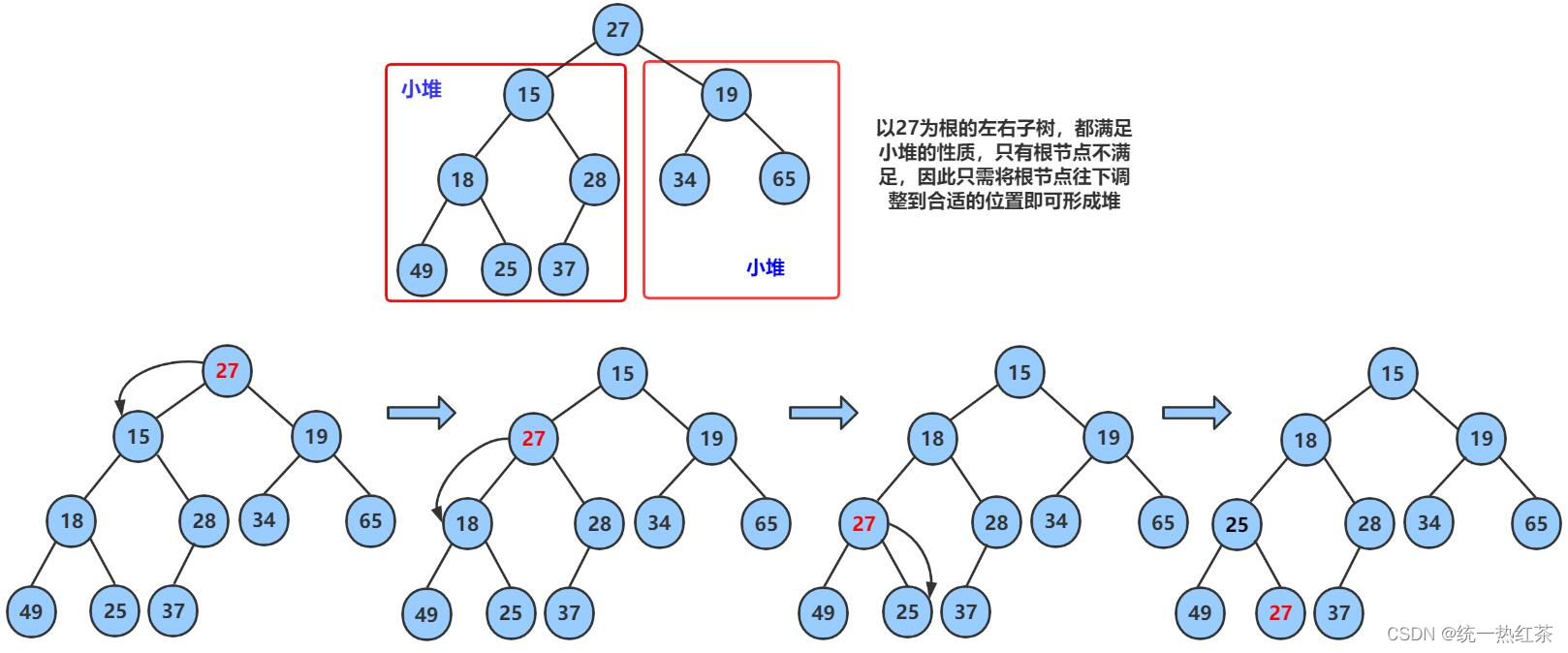
【数据结构】堆(C语言)
今天我们来学习堆,它也是二叉树的一种(我滴神树!) 目录 堆的介绍:堆的代码实现:堆的结构体创建:堆的初始化:堆的销毁:堆的push:堆的pop:判空 &am…...

使用 Raspberry Pi、Golang 和 HERE XYZ 制作实时地图
到目前为止,您可能已经看过我的一些与 Raspberry Pi 和位置数据相关的教程。我是这些小型物联网 (IoT) 设备的忠实粉丝,并编写了有关使用 Golang 进行 WLAN 定位 和 使用 Node.js 进行 GPS 定位的教程。 我想继续沿着 Golang 路线,做一个关于…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
