二分查找由浅入深--算法--java
二分查找
- 写在开头
- 算法前提:
- 算法逻辑
- 算法实现
- 简单实现
- left+right可能超过int表示的最大限度
- 代码分析和变换
- 更多需求:求索引最小的值
- java二分API
- 应用
- 基础题
- 思考难度
- 方法
写在开头
二分查找应该是算比较简单的这种算法了,我本以为还可以。但有时候也没想到过能这么用,最震惊的就是对答案进行二分了。而且有时候不够熟练,还有我遇到的问题都总结一下。算法前提:
数据需要有序,可以重复元素。
算法逻辑
以升序数列为例,
比较一个元素与数列中的中间位置的元素的大小
1.如果比中间位置的元素大,则继续在后半部分的数列中进行二分查找;
2.如果比中间位置的元素小,则在数列的前半部分进行比较;
3.如果相等,则找到了元素的位置。
每次比较的数列长度都会是之前数列的一半,直到找到相等元素的位置或者最终没有找到要找的元素。
算法实现
简单实现
// 二分查找
public static int binarySearch(int[] a, int target) {int left = 0;int right = a.length - 1;while (left <= right) {int mid = (left + right) / 2;if (a[mid] == target) {return mid;} else if (a[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;
}
left+right可能超过int表示的最大限度
出现结果:mid算出来为负数。
java中int类型占4个字节的最大值是 231−12^{31}-1231−1, 即 2147483647
如果超过了表示范围,则会发送越界,则会加到符号位。
那么我们可以进行无符号右移就可以完成除法运算,和解决越界问题了。
(有没有可能超过32位,2个int数相加最大不会大于232−12^{32}-1232−1,所以一定不会超过int存储)
所以代码修改如下
int mid =(left+right)>>>2;
代码分析和变换
简单实现里面:还是建议把等值放到最后面,因为等值的可能性是最低的,这样也就可以降低判断的次数。
把谁放第一判断,则那一边效率会高一点,如果下代码,如果数据偏右,则效率可能高些。
if (a[mid] < target) {left = mid + 1;
} else if (a[mid] > target) {right = mid - 1;
} else {return mid;
}
最坏情况O(logn)O(\log n)O(logn)
最好情况O(1)O(1)O(1)
空间复杂度O(1)O(1)O(1)
均衡性:每次循环必定需要一次判断
public static int binarySearch(int[] a, int target) {int left = 0;int right = a.length;while (right - left <= 1) {int mid = (left + right) / 2;if (target < a[mid]) {right = mid;} else{left = mid;}}return a[i]==target?i:-1;}return -1;
}
时间复杂度Ω(logn)\Omega(\log n)Ω(logn)
更多需求:求索引最小的值
public static int binarySearchMin(int[] a, int target){int l=0,r=a.length;while(l < r){int m = (l + r) >>> 1;if (a[m] < target)l = m + 1;elser = m;}return l;
}
注意:如果数据不存在则返回的是切入点
不想这样的话可以
return a[l]==target?l:-(l+1);
java二分API
在Arrays类中有一个binarySearch()的方法可以返回数组中二分查找的结果
使用:
binarySearch(数组,key)
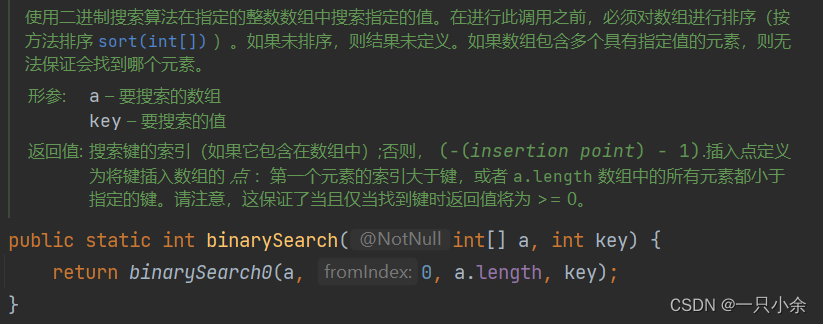
源代码:和我们实现的差不多。
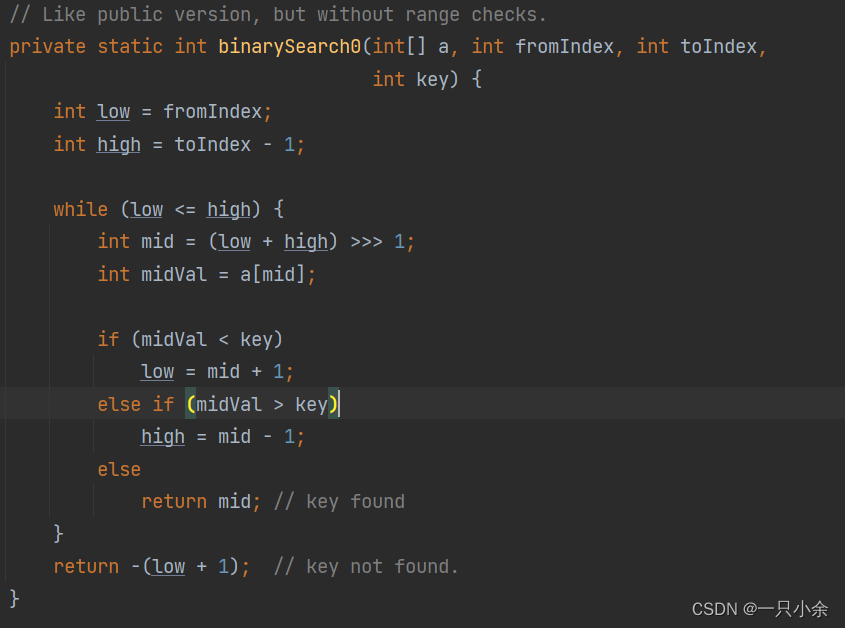
格外的api
public static int binarySearch(int[] a, int fromIndex, int toIndex,int key)
fromIndex – 要搜索的第一个元素(包括)的索引
toIndex – 要搜索的最后一个元素(独占)的索引
应用
基础题
力扣278. 第一个错误的版本
解决:二分求索引最小
public class Solution extends VersionControl {public int firstBadVersion(int n) {int l=1;int r=n;while(l < r){int mid=(l+r)>>>1;if(isBadVersion(mid))r=mid;elsel=mid+1;}return l;}
}
leetcode34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
public int[] searchRange(int[] nums, int target) {int x = -1, y = -1;int l = 0, r = nums.length - 1;while (l < r) {int m = (l + r) >>> 1;if (nums[m] >= target)r = m;elsel = m + 1;}if (l < 0 || l > nums.length-1||nums[l] != target)return new int[]{x, y};x = l;r = nums.length - 1;while (l < r) {int m = (l + r) >>> 1;if (nums[m] > target)r = m - 1;elsel = m + 1;}y = l - 1;return new int[]{x, y};}
思考难度
leetcode 4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数.
算法的时间复杂度应该为 O(log(m+n)) 。
分析:
l=n+m为总数
求中位数:
- 如果l为奇数,则中位数为(l+1)/2的位置
- 如果为偶数,则中位数为(l+1)/2和(l+2)/2的平均数
即求指定位置k的数。
在每次比较k/2位置的2个数组上的数如果n1[k/2]<n2[k/2]则n1上k/2以前的数都在合并k位置之前。
如:
n1=[1,2,4,5,6]
n2=[2,3,5,7,9,11]
l=11 k=6 k/2=3
n1[3]=4<n2[3]=5
则1,2,4都会在合并数组k位置的前面
n1=[5,6]
n2[2,3,5,7,9,11]
此时k=3 k/2=1
比较5和2
所以
n1=[5,6]
n2[3.5,7,9,11]
此时k=2,k/2=1
去掉一个3
k=1
返回2个最开始的小值就行。
问:
1.能不能在k=2的时候返回大值呢?
不行的,如果一个数组1,2另一个3,4就不可用。
2.如果k/2大于一个数组长度呢?
那就取这个数组最后一个就行了,这样要么不用考虑这个数组了,要么长数组会变短。
public double findMedianSortedArrays(int[] nums1, int[] nums2) {int n = nums1.length;int m = nums2.length;int left = (n + m + 1) / 2;int right = (n + m + 2) / 2;//将偶数和奇数的情况合并,如果是奇数,会求两次同样的 k 。return (search(nums1, 0, nums2, 0, left) + search(nums1, 0, nums2, 0, right)) * 0.5;
}
// a为一个数组,i为这个数组剩下的.b同理
// k 为需要求的数的位置
public int search(int[] a,int i,int[] b,int j,int k){//求剩余长度int l1 = a.length-i;int l2 = b.length-j;//调整l1永远为短的if(l1>l2) return search(b,j,a,i,k);if(l1 == 0) return b[j+k-1];if (k == 1) return Math.min(a[i], b[j]);int q = k/2;//x,y 为索引int x = i + Math.min(q,l1) - 1;int y = j + Math.min(q,l2) - 1;if(a[x] > b[y])return search(a,i,b,y+1,k-(y-j+1));elsereturn search(a,x+1,b,j,k-(x-i+1));
}
方法
leetcode2439. 最小化数组中的最大值
给你一个下标从 0 开始的数组 nums ,它含有 n 个非负整数。
每一步操作中,你需要:
选择一个满足 1 <= i < n 的整数 i ,且 nums[i] > 0 。
将 nums[i] 减 1 。
将 nums[i - 1] 加 1 。
你可以对数组执行任意次上述操作,请你返回可以得到的 nums 数组中最大值最小为多少。
示例 1:
输入:nums = [3,7,1,6]
输出:5
解释:
一串最优操作是:
1. 选择 i = 1 ,nums 变为 [4,6,1,6] 。
2. 选择 i = 3 ,nums 变为 [4,6,2,5] 。
3. 选择 i = 1 ,nums 变为 [5,5,2,5] 。
nums 中最大值为 5 。无法得到比 5 更小的最大值。
所以我们返回 5 。
示例 2:
输入:nums = [10,1]
输出:10
解释:
最优解是不改动 nums ,10 是最大值,所以返回 10 。
提示:
n==nums.lengthn == nums.lengthn==nums.length
2<=n<=1052 <= n <= 10^52<=n<=105
0<=nums[i]<=1090 <= nums[i] <= 10^90<=nums[i]<=109
分析:
这个题目是我第一次遇到二分答案的题目,属实打开了我的新世界了。
对答案进行二分。
1.根据题目要求右边只能降,左边只能升。第一个值可以从后面所有的值里面取过来。
2.所以对一个最大值m是否符合条件,我们可以从左往右遍历,如果这个数k比他小那么,则需要m-k个位置,如果比他大,那么把需要减掉,这时如果需求为负数,则一定不是这个数。
但是最大值如果很大,那么都会是需要位置而没有剪掉的呢?
因为我们二分会去找最小可能,即找到符合的最左边就行。
public int minimizeArrayValue(int[] nums) {int l = 0,r = Integer.MAX_VALUE;while(l < r){int m = (l+r)>>>1;if(check(nums,m))r = m;elsel = m+1;}return r;
}
public static boolean check(int[]a,int m){long count = 0;for(int i:a){if(i<m)count+=m-i;else{count -= i-m;if(count < 0)return false;}}return true;
}
相关文章:

二分查找由浅入深--算法--java
二分查找写在开头算法前提:算法逻辑算法实现简单实现leftright可能超过int表示的最大限度代码分析和变换更多需求:求索引最小的值java二分API应用基础题思考难度方法写在开头 二分查找应该是算比较简单的这种算法了,我本以为还可以。但有时候…...
【学习】笔记本电脑重新安装系统win10
安装系统有很多方法: 软件安装制作启动u盘本文使用的方法就是启动盘安装: 1.首先下载iso镜像文件: msdn我告诉你:MSDN, 我告诉你 - 做一个安静的工具站 (itellyou.cn) 2.下载启动盘制作工具: 制作启动盘rufus:Rufus - 轻松创建 USB 启动盘 3.官网下载: https://do…...
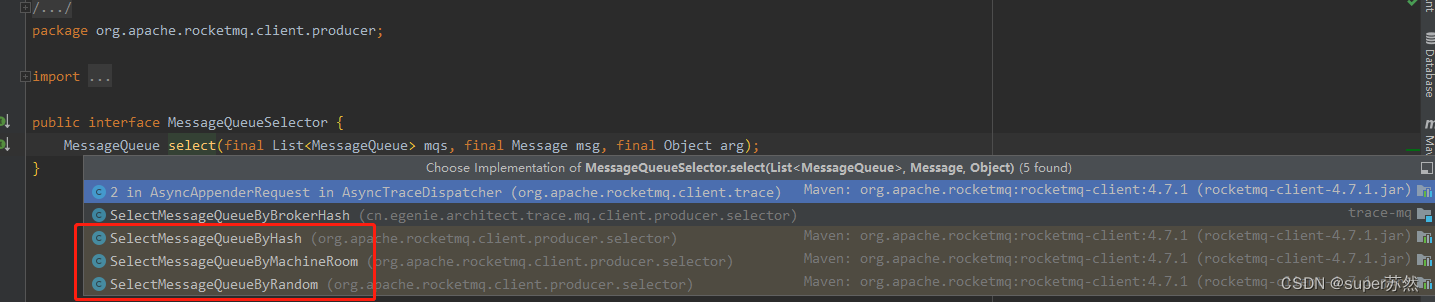
RocketMQ的一些使用理解
1.RocketMQ的生产者生产负载策略(3种) (1)SelectMessageQueueByHash (一致性hash) (2)SelectMessageQueueByMachineRoom (机器随机) (3)SelectMessageQueueByRandom (随机) 第1种一…...

Java枚举详解
一.枚举 1.为什么有枚举? 如果我们的程序需要表示固定的几个值: 比如季节:spring (春),summer(夏),autumn(秋),winter(冬) 用常量表示: public static final int SEASON_SPRING 1;public st…...

虚拟机上安装openKylin详细步骤总结
一、创建虚拟机 首先获取操作系统安装镜像文件: 链接:https://pan.baidu.com/s/1tSuXmDk2ZILR4ieee6iImw?pwdcy47 提取码:cy47 (1-1)进入新虚拟机创建向导,选择“自定义”: (1-…...
)
夜天之书 #74 企业开源的软件协议模型实践(Part 2)
在上一篇文章中,我介绍了企业开源的完全开放源码策略及其风险。完全开放源码,即以符合开源定义的软件协议发布企业自研软件的情形。本文介绍应对完全开放源码后的风险的第一种策略:提高市场占有率与开放标准。与其说是策略,不如说…...

2.webpack实时打包
简介 上一章已经实现了使用 webpack 构建了一个简单的项目;但是我们发现,每次修改了 index.js 需要重新执行 cnpm run dev 命令重新构建 main.js;这在开发阶段是无法忍受的,因为这样调式将浪费大量的时间;还好 webpac…...

KingbaseES V8R3 表加密
前言 透明加密是指将数据库page加密后写入磁盘,当需要读取对应page时进行加密读取。此过程对于用户是透明, 用户无需干预。 该文档进行数据库V8R3版本测试透明加密功能,需要说明,该版本发布时间早于V8R6,所以只能进行表…...

2 为社么软件架构很重要?
2 为社么软件架构很重要? 啊,建造,建造! 这是所有艺术中最崇高的艺术。 — 亨利沃兹沃思朗费罗 如果架构是答案,那么问题是什么? 本章从技术角度重点介绍架构的重要性。我们将研究面包师的十几个最重要…...
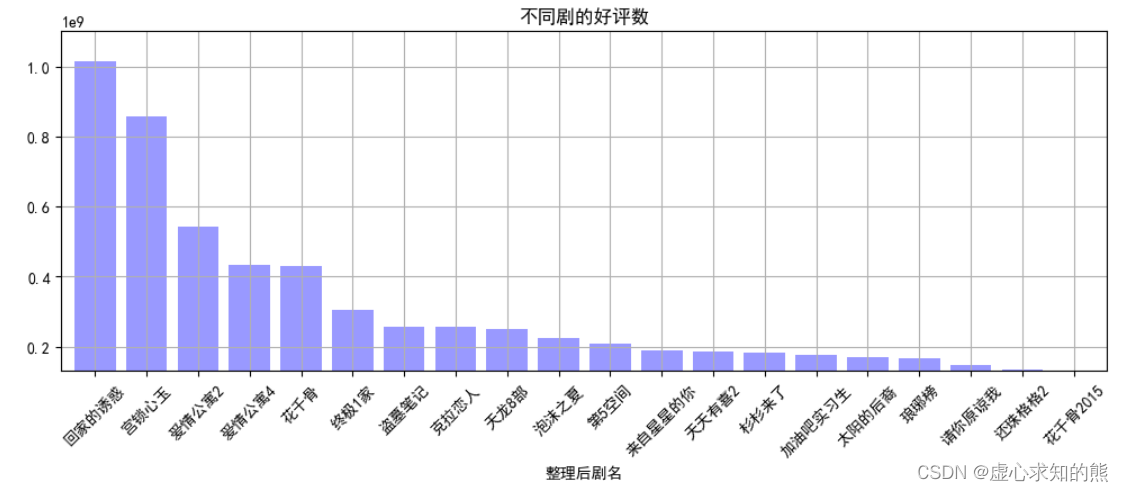
Python 之 Pandas merge() 函数、set_index() 函数、drop_duplicates() 函数和 tolist() 函数
文章目录一、merge() 函数1. inner2. left 和 right3. outer二、set_index() 函数三、drop_duplicates() 函数四、tolist() 函数五、视频数据分析案例1. 问题要求2. 解决过程在最开始,我们先导入常规的 numpy 和 pandas 库。 import numpy as np import pandas as …...
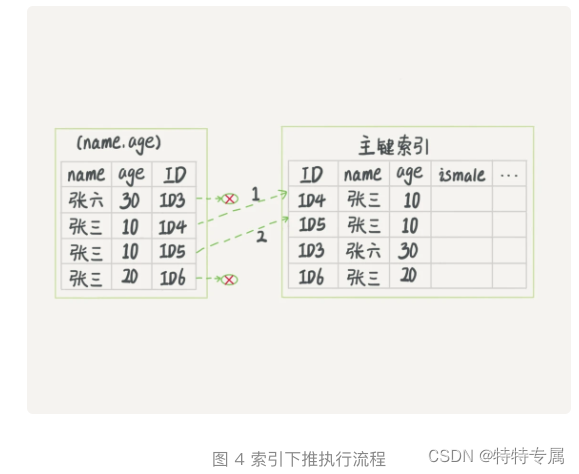
MySQL实战之深入浅出索引(下)
1.前言 在上一篇文章中,我们介绍了InnoDB索引的数据结构模型,今天我们再继续聊一下跟MySQL索引有关的概念。 在介绍之前,我们先看一个问题: 表初始化语句 mysql> create table T ( ID int primary key, k int NOT NULL DEFA…...
leetcode1539. 第 k 个缺失的正整数)
(二分查找)leetcode1539. 第 k 个缺失的正整数
文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目 1、题目描述 给你一个 严格升序排列 的正整数数组 arr 和一个整数 k 。 请你找到这个数组里第 k 个缺失的正整数。 示例 1: 输入&…...

yaml文件格式详解及实例
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录yaml简介yaml语法规则Yaml语法实例数组…...

AOP在PowerJob中的使用,缓存锁保证并发安全,知识细节全总结
这是一篇简简单单的文章,需要你简简单单看一眼就好,如果有不明白的地方,欢迎留言讨论。 在之前的文章中出现过一次AOP的使用,就是在运行任务之前,需要判断一下,触发该任务执行的server,是不是数…...
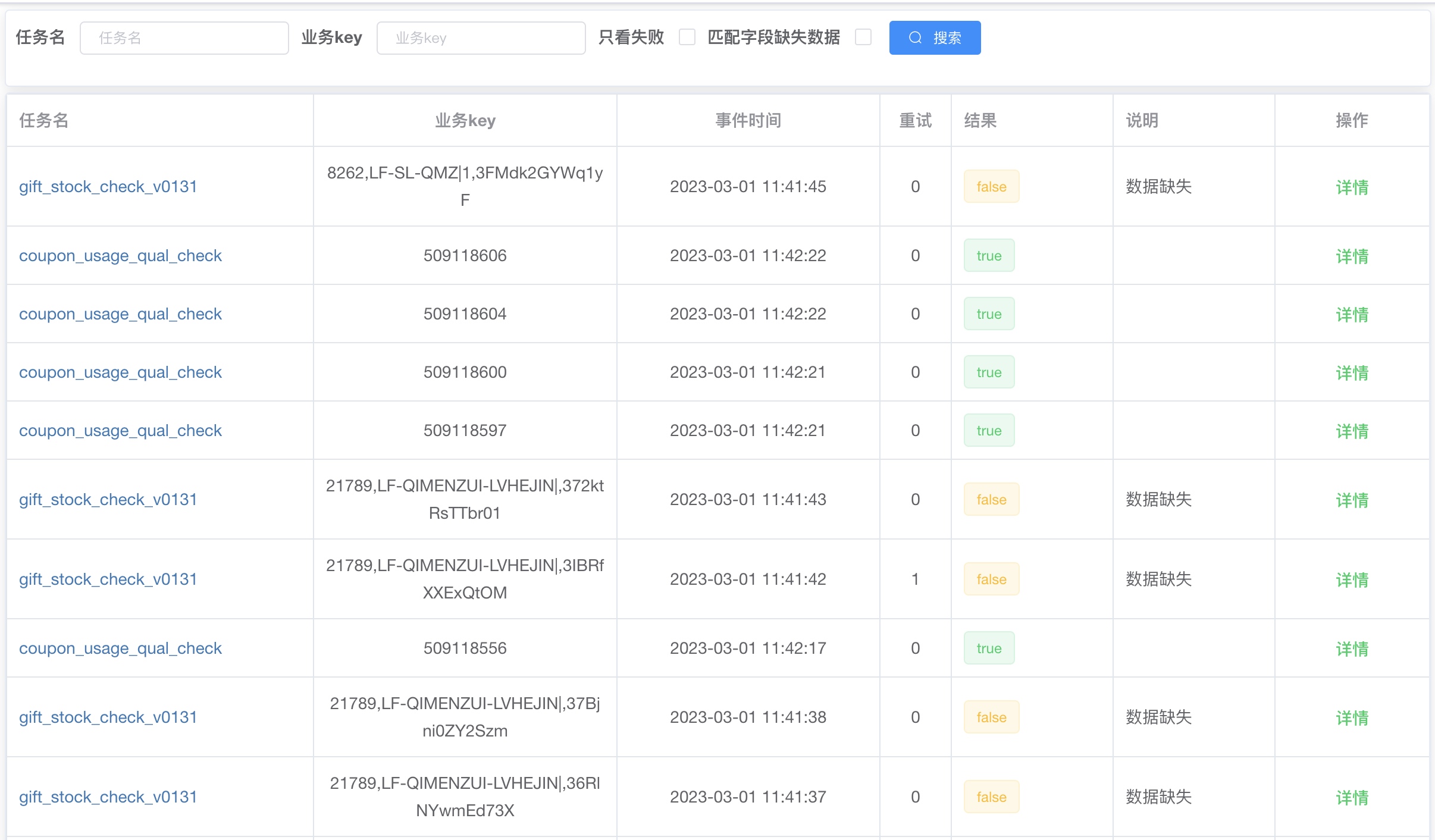
对账平台设计
背景 随着公司业务的蓬勃发展,交易履约清结算业务的复杂性也在不断的增高,资金以及各种数据的一致性和准确性也变得越发重要。 以交易链路为例,存在着如下一些潜在的不一致场景: 订单支付成功了,但是订单状态却还是“…...
JavaEE进阶第五课:SpringBoot的创建和使用
上篇文章介绍了Bean 作用域和生命周期,这篇文章我们将会介绍SpringBoot的创建和使用 目录1.为什么要学习StringBoot1.1什么是SpringBoot1.2SpringBoot的优点2.如何用Idea创建SpringBoot项目3.项目目录介绍和运行3.1输入Helloworld结尾1.为什么要学习StringBoot 在前…...

我带过的一名C++实习生——Z同学
刚开始带Z同学,吃饭聊天时,我顺便了解了下他的擅长:linux平台下C、C网络编程。 接下来的实习,主要分为两个阶段:小组公共培训和项目实训。 小组公共培训为期2周,主要学习和了解公司文化制度,讲师…...

面试题13. 机器人的运动范围
面试题13. 机器人的运动范围 难度:middle\color{orange}{middle}middle 题目描述 地上有一个 mmm 行 nnn 列的方格,从坐标 [0,0][0,0][0,0] 到坐标 [m−1,n−1][m-1,n-1][m−1,n−1] 。一个机器人从坐标 [0,0][0, 0][0,0] 的格子开始移动,它…...

LeetCode189_189. 轮转数组
LeetCode189_189. 轮转数组 一、描述 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,…...

java Files和Paths的使用详解 附有使用demo
前言 Java Files和Paths是Java 7中引入的新API,用于处理文件和目录。Files类提供了许多有用的静态方法来操作文件和目录,而Path类则表示文件系统中的路径。 创建文件和目录 在Java中创建文件和目录非常简单。我们可以使用Files类的createFile()方法和…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...
