使用VC++设计程序:实现常见的三种图像插值算法:最近邻插值,双线性插值,立方卷积插值
图像放大的三种插值算法
获取源工程可访问gitee可在此工程的基础上进行学习。
该工程的其他文章:
01- 一元熵值、二维熵值
02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转
03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器
04-分段线性变换,直方图均衡化、锐化处理
05-基于拉普拉斯算子、Canny的边缘检测功能、实现Otsu分割方法
文章目录
- 图像放大的三种插值算法
- 实验内容
- 一、 插值算法的原理
- 1. 最近邻插值
- 2. 双线性插值
- 3. 立方卷积插值
- 二、 实验代码与现象图
- 1. 最近邻插值
- 2. 双线性插值
- 3.立方卷积插值
实验内容
B–(3)研究放大图像时使用的插值算法,使用VC++实现常见的三种图像插值算法:最近邻插值,双线性插值,立方卷积插值。通过实验验证其效果。
一、 插值算法的原理
1. 最近邻插值
最近邻插值是一种简单的插值方法,它选择离目标位置最近的已知像素值。对于二维图像上的插值,最近邻插值的公式为:
I new ( x , y ) = I old ( round ( x ) , round ( y ) ) I_{\text{new}}(x, y) = I_{\text{old}}\left(\text{round}(x), \text{round}(y)\right) Inew(x,y)=Iold(round(x),round(y))
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $ I_{\text{old}}(x’, y’) $是原始图像中最近邻的已知像素值,其中 $ (x’, y’) $ 由 $ (x, y) $ 四舍五入得到。
2. 双线性插值
双线性插值考虑了目标位置周围的四个最近的已知像素值,并根据其相对位置进行加权平均。对于二维图像上的插值,双线性插值的公式为:
I new ( x , y ) = ( 1 − α ) ( 1 − β ) I old ( x 1 , y 1 ) + α ( 1 − β ) I old ( x 2 , y 1 ) + ( 1 − α ) β I old ( x 1 , y 2 ) + α β I old ( x 2 , y 2 ) I_{\text{new}}(x, y) = (1 - \alpha)(1 - \beta)I_{\text{old}}(x_1, y_1) + \alpha(1 - \beta)I_{\text{old}}(x_2, y_1) + (1 - \alpha)\beta I_{\text{old}}(x_1, y_2) + \alpha \beta I_{\text{old}}(x_2, y_2) Inew(x,y)=(1−α)(1−β)Iold(x1,y1)+α(1−β)Iold(x2,y1)+(1−α)βIold(x1,y2)+αβIold(x2,y2)
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $ I_{\text{old}}(x_i, y_i)$是原始图像中四个最近邻的已知像素值,其中 $ (x_i, y_i) $ 是目标位置的四个相邻像素的坐标。
- $ \alpha = x - x_1 $ 和 $ \beta = y - y_1$。
双线性插值算法涉及到目标位置周围的四个最近邻的已知像素值。这四个最近邻的像素可以通过目标位置坐标的整数部分和小数部分来确定。假设目标位置的坐标为 ((x, y)),则这四个最近邻的坐标可以表示为 ((x_1, y_1), (x_2, y_1), (x_1, y_2), (x_2, y_2)),其中:
- x 1 = ⌊ x ⌋ x_1 = \lfloor x \rfloor x1=⌊x⌋ 是 x x x的整数部分;
- x 2 = ⌈ x ⌉ x_2 = \lceil x \rceil x2=⌈x⌉ 是 x x x的整数部分加一;
- y 1 = ⌊ y ⌋ y_1 = \lfloor y \rfloor y1=⌊y⌋ 是 y y y 的整数部分;
- y 2 = ⌈ y ⌉ y_2 = \lceil y \rceil y2=⌈y⌉ 是 y y y 的整数部分加一。
这四个最近邻的坐标形成了一个矩形区域,如下图所示:
(x1, y1) ---------- (x2, y1)| || || |
(x1, y2) ---------- (x2, y2)
3. 立方卷积插值
立方卷积插值考虑了目标位置周围的八个最近的已知像素值,并使用立方卷积核进行加权平均。对于二维图像上的插值,立方卷积插值的公式较为复杂,其中涉及到立方卷积核的权重计算。
I new ( x , y ) = ∑ i = − 1 2 ∑ j = − 1 2 w ( i , j ) I old ( x + i , y + j ) I_{\text{new}}(x, y) = \sum_{i = -1}^{2} \sum_{j = -1}^{2} w(i, j)I_{\text{old}}(x + i, y + j) Inew(x,y)=i=−1∑2j=−1∑2w(i,j)Iold(x+i,y+j)
其中:
- $ I_{\text{new}}(x, y) $ 是目标位置的新像素值。
- $I_{\text{old}}(x + i, y + j) $ 是原始图像中八个最近邻的已知像素值,其中 $i $ 和 $j $取值为 -1, 0, 1, 2。
- $ w(i, j) $ 是立方卷积核的权重,通常采用一些特定的卷积核形式,如 Bicubic 插值。
在立方卷积插值中,涉及到的是8个点。以下是正确的描述:
对于立方卷积插值,考虑目标位置 ( x , y ) (x, y) (x,y) 周围的8个最近邻点,其坐标可以表示为 ( x i , y j ) (x_i, y_j) (xi,yj),其中:
x i = x − 1 , 0 , 1 , 2 x_i = x - 1, 0, 1, 2 xi=x−1,0,1,2
y j = y − 1 , 0 , 1 , 2 y_j = y - 1, 0, 1, 2 yj=y−1,0,1,2
这样,可以得到一个包含8个点的矩阵,如下所示:
(x-1, y-1) | (x, y-1) | (x+1, y-1) | (x+2, y-1)
(x-1, y) | (x, y) | (x+1, y) | (x+2, y)
(x-1, y+1) | (x, y+1) | (x+1, y+1) | (x+2, y+1)
(x-1, y+2) | (x, y+2) | (x+1, y+2) | (x+2, y+2)
这里的坐标形成了一个4x4的矩阵,但在立方卷积插值中,只需要考虑中间的8个点。这8个点的坐标将用于计算插值权重。
二、 实验代码与现象图
1. 最近邻插值
void CImageProcessingView::OnGeoResizing()
{// 实验 图像缩放//MessageBox("请在这里添加图像缩放的代码");// 获得当前文档对象
CImageProcessingDoc* pDoc = GetDocument();// 判断图像是否已被加载if( pDoc->m_pDibInit->IsEmpty() ){MessageBox("图像未加载");return;}int width = pDoc->m_pDibInit->GetWidth();int height = pDoc->m_pDibInit->GetHeight();int bitCount = pDoc->m_pDibInit->GetBitCount();// 将 m_pDibInit 拷贝至 m_pDibTestpDoc->m_pDibTest->CloneDib(pDoc->m_pDibInit);// 考虑将图像放大两倍的情况 float nResizing = 2;// 获得新的图像高度int newWidth = width*nResizing;int newHeight = height*nResizing;pDoc->m_pDibTest->SetWidthHeight(newWidth, newHeight);//*****************************图像的插值1最近邻插值算法************//int i=0;int j=0;float src_x, src_y;RGBQUAD Quad1;for(i=0;i<newWidth;i++)for(j=0;j<newHeight;j++){src_x = (i / nResizing) + 0.5; //四舍五入src_y = (j / nResizing) + 0.5;Quad1=pDoc->m_pDibInit->GetPixelColor(src_x,src_y);pDoc->m_pDibTest->SetPixelColor(i,j,&Quad1);}// 交换 m_pDibInit 与 m_pDibTest 指针CDib* pTmp = pDoc->m_pDibInit;pDoc->m_pDibInit = pDoc->m_pDibTest;pDoc->m_pDibTest = pTmp; // 设置脏标记pDoc->SetModifiedFlag(TRUE);// 更新视图pDoc->UpdateAllViews(NULL);
}实验现象.
图像放大2倍
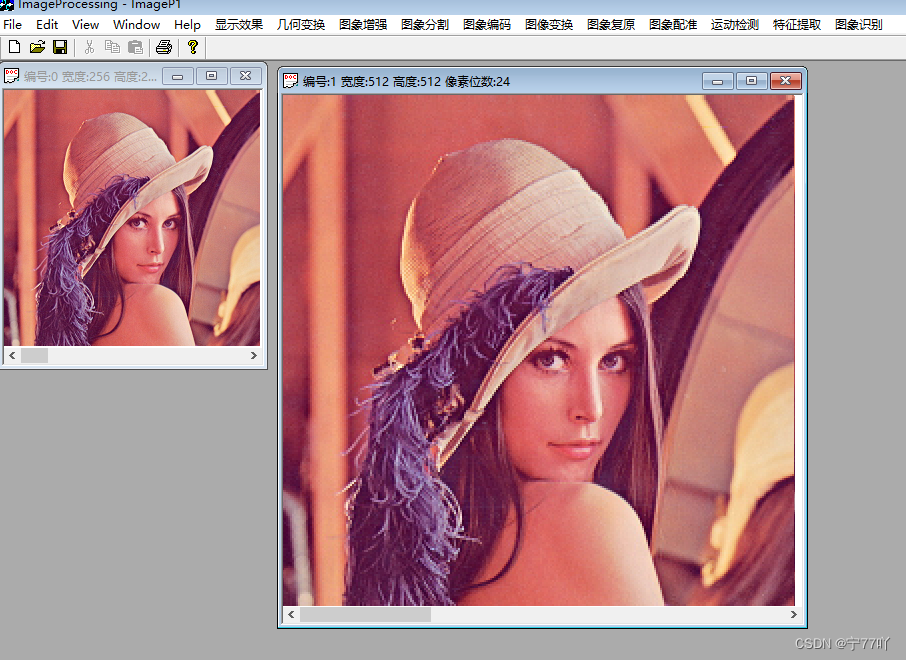
2. 双线性插值
int i=0;int j=0;for(i=0;i<newWidth;i++)for(j=0;j<newHeight;j++){int x=i/nResizing, y = j / nResizing; //定位,找周围四个点float u = i / nResizing,v = j / nResizing; //注意这个类型u =u - x; //所占权重系数v =v - y;int gray0 , gray1 , gray2 , gray3 , GRAY ;gray0 = pDoc->m_pDibInit->GetPixelGray(x, y);//边界处理 非补零if (x + 1 < 256)gray1 = pDoc->m_pDibInit->GetPixelGray(x+1, y);elsegray1 = pDoc->m_pDibInit->GetPixelGray(x, y);if (y + 1 < 256)gray2 = pDoc->m_pDibInit->GetPixelGray(x, y + 1);elsegray2 = pDoc->m_pDibInit->GetPixelGray(x, y);if (x + 1 < 256 && y + 1 < 256)gray3 = pDoc->m_pDibInit->GetPixelGray(x + 1, y + 1);elsegray3 = pDoc->m_pDibInit->GetPixelGray(x, y);GRAY = (1 - u) * (1 - v) * gray0 + (1 - u) * v * gray2 + u * (1 - v) * gray1 + u * v * gray3;pDoc->m_pDibTest->SetPixelGray(i, j, GRAY);}// 交换 m_pDibInit 与 m_pDibTest 指针CDib* pTmp = pDoc->m_pDibInit;pDoc->m_pDibInit = pDoc->m_pDibTest;pDoc->m_pDibTest = pTmp;
实验效果图.
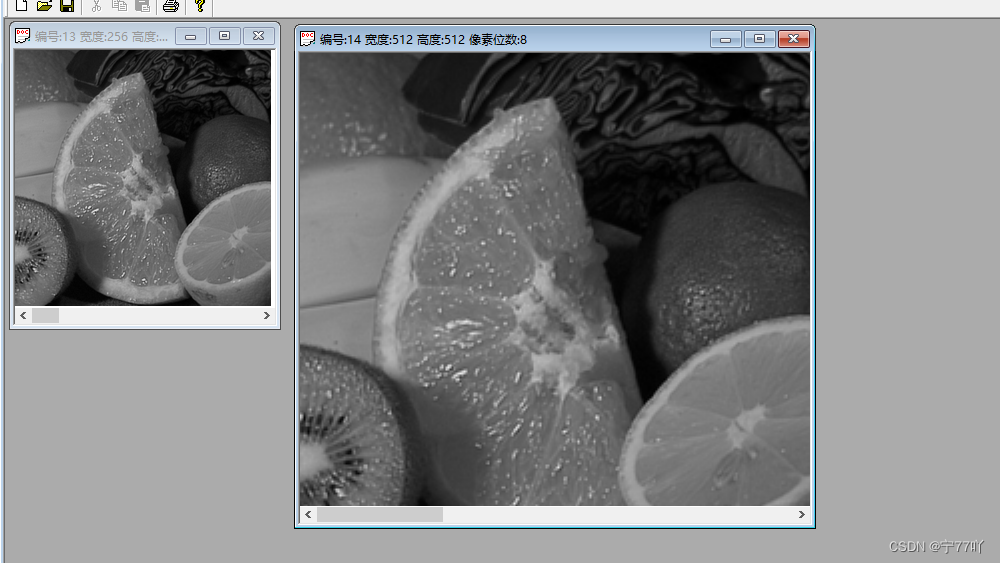
3.立方卷积插值
int a = -0.5; //系数for(int i=0;i<newWidth;i++)for (int j = 0; j < newHeight; j++){int x[4] = { 0 }, y[4] = { 0 };x[1] = i / nResizing, y[1] = j / nResizing; //找点,(1,1)位置x[0] = x[1] - 1; y[0] = y[1] - 1;x[2] = x[1] + 1; y[2] = y[1] + 1;x[3] = x[1] + 2; y[3] = y[1] + 2;float u = (i) / nResizing, v = (j) / nResizing;u =u - x[1]; //所占权重系数(大于0小于1)v =v - y[1];int gray[4][4] = { 0 };float w_x[4] = { 0 }, w_y[4] = { 0 };w_x[0] = 1 + u; w_x[1] = u; w_x[2] = 1 - u; w_x[3] = 2 - u;w_y[0] = 1 + v; w_y[1] = v; w_y[2] = 1 - v; w_y[3] = 2 - v;float W_x[4] = { 0 }, W_y[4] = { 0 };for (int k = 0; k < 4; k++) //计算x和y的权重{if (w_x[k] <= 1 && w_x[k] >= -1)W_x[k] = (a + 2) * pow(w_x[k], 3) - (a + 3) * pow(w_x[k], 2) + 1;else if (w_x[k] > 1 && w_x[k] < 2) W_x[k] = a * pow(w_x[k], 3) - 5 * a * pow(w_x[k], 2) + 8 * a * w_x[k] - 4 * a;elseW_x[k] = 0;if (w_y[k] <= 1 && w_y[k] >= -1)W_y[k] = (a + 2) * pow(w_y[k], 3) - (a + 3) * pow(w_y[k], 2) + 1;else if (w_y[k] > 1 && w_y[k] < 2)W_y[k] = a * pow(w_y[k], 3) - 5 * a * pow(w_y[k], 2) + 8 * a * w_y[k] - 4 * a;elseW_y[k] = 0;}for(int k=0;k<4;k++)for (int m = 0; m < 4; m++){if (x[k] > 0 && x[k]<height && y[m] > 0 && y[m] < width) //判断边界gray[k][m] = pDoc->m_pDibInit->GetPixelGray(x[k], y[m]);elsegray[k][m] = 0;}int Pix_gray = 0; //最终计算得到的灰度值for(int k=0;k<4;k++)for (int m = 0; m < 4; m++){Pix_gray += gray[k][m] * W_x[k] * W_y[m];}pDoc->m_pDibTest->SetPixelGray(i, j, Pix_gray);}
实验效果图.
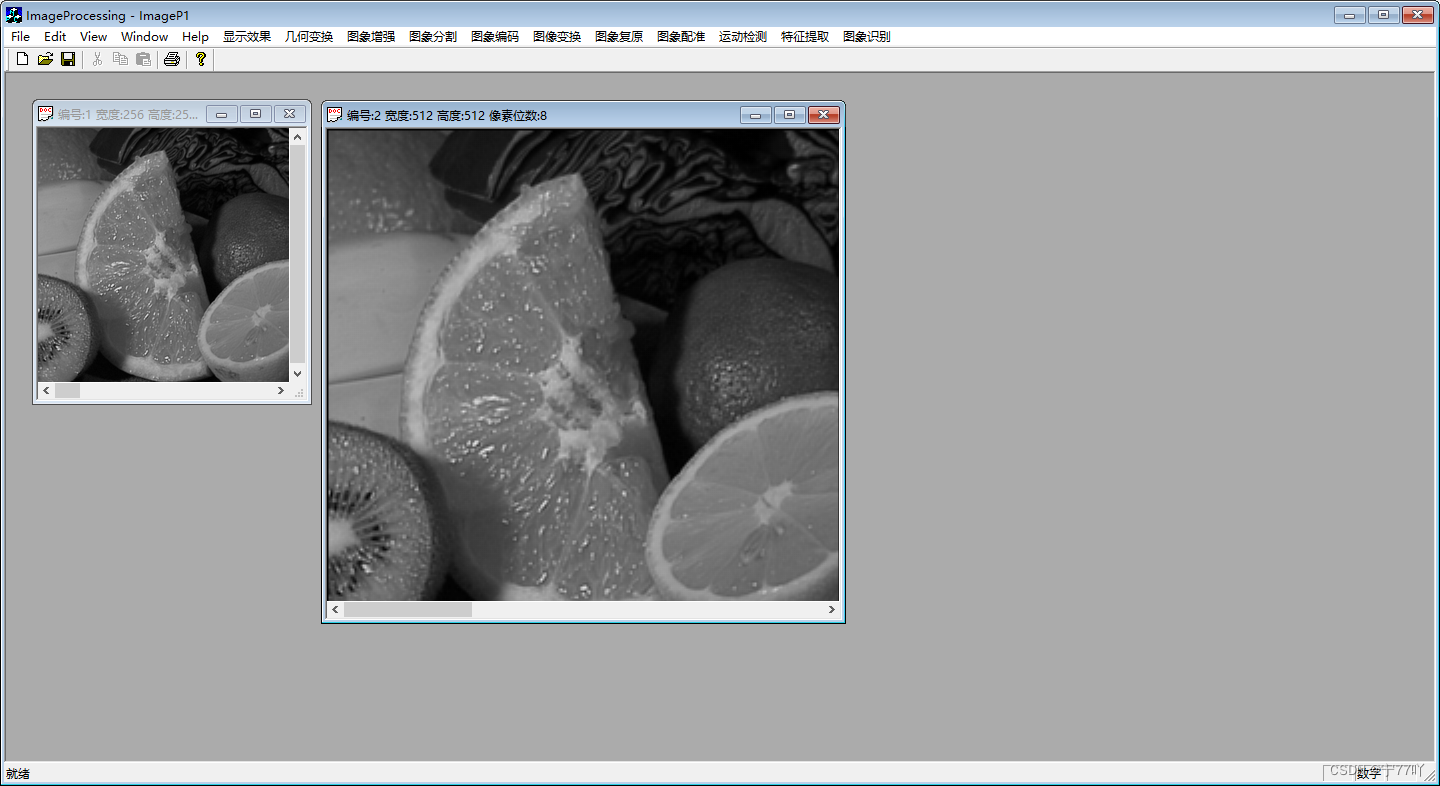
相关文章:

使用VC++设计程序:实现常见的三种图像插值算法:最近邻插值,双线性插值,立方卷积插值
图像放大的三种插值算法 获取源工程可访问gitee可在此工程的基础上进行学习。 该工程的其他文章: 01- 一元熵值、二维熵值 02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转 03-邻域平均平滑算法、中值滤波算法、K近邻均值滤波器 04-…...

多级嵌套vue同步调用用法
//需求 要求同步调用initGame2方法 //调用方法 this.initSocket(); //定义方法为同步 async initSocket() { //调用为同步 await this.initGame2(); //定义方法为同步 async initGame2() {const e await w({ url: //定义w方法 const w e.create({ baseURL: http://my_url:8…...
C#,《小白学程序》第八课:列表(List)其二,编制《高铁列车时刻表》与时间DateTime
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary&g…...

高德地图使用逆地理编码服务
进入高德地图开发者平台申请web服务,并获取web服务生成的key下面是高德地图官网的逆地理编码服务使用说明https://lbs.amap.com/api/webservice/guide/api/georegeo/ getAddressByLocation(latitude, longitude) {const key key; // 高德地图key密钥const url h…...

ArgoCD基本组件
ArgoCD有5个基本组件, $ kubectl get po -n argocd NAME READY STATUS RESTARTS AGE argocd-application-controller-0 1/1 Running 0 19h argocd-dex-server-767fb49f59-7rxn7 1/1 Running 0…...
技术分享 | 在 IDE 插件开发中接入 JCEF 框架
项目背景 当前的开发环境存在多种不同语言的 IDE,如 JetBrains 全家桶、Eclipse、Android Studio 和 VS Code 等等。由于每个 IDE 各有其特定的语言和平台要求,因此开发 IDE 插件时,需要投入大量资源才能尽可能覆盖大部分工具。同时…...
ubuntu 使用webrtc_ros 编译linux webrtc库
ubuntu 使用webrtc_ros 编译linux webrtc库 webrtc_ros 使用WebRTC流式传输ROS图像主题 该节点提供了一个WebRTC对等方,可以将其配置为流ROS图像主题并接收发布到ROS图像主题的流。 该节点托管一个提供简单测试页面的Web服务器,并提供可用于创建和配置W…...
网络通信基础概念介绍
网络通信基础概念介绍 局域网LAN 局域网,即 Local Area Network,简称LAN。 局域网内的主机之间能方便的进行网络通信,又称为内网;局域网和局域网之间在没有连接的情况下,是无法通信的。 局域网是指在一个相对较小的…...

quickapp_快应用_全局数据
全局数据 [1]本地数据存储[2] 数据缓存问题 有时在接口请求的某个数据需要在多个页面使用,此时有2个方法 [1] 将数据存储在本地—> 等价于浏览器的localStorage[2] 将数据存储在数据缓存中 -> 等价于vue中的vuex [1]本地数据存储 官方文档:官方…...

Unity接入Protobuf介绍
Protobuf介绍 Protobuf(Protocol Buffers,简称Proto)是一种轻量级和高效率的数据序列化格式,由Google公司开发。与XML和JSON等文本格式不同,Protobuf是一种二进制格式,它具有更小的体积和更快的速度。在大…...

【anaconda】numpy.dot 向量点乘小技巧
假设向量A[1,1], 向量B[2,3]。如果想知道他们的内积就可以输入如下代码: 当然,如果是两个列向量相乘,肯定是不对的 但是如果没有维度也一样可以求得内积,而且结果不会套在列表里...

YOLOv5小目标检测层
目录 一、原理 二、yaml配置文件 一、原理 小目标检测层,就是增加一个检测头,增加一层锚框,用来检测输入图像中像素较小的目标 二、yaml配置文件 # YOLOv5 🚀 by Ultralytics, GPL-3.0 license# Parameters nc: 3 # number of classes depth_multiple: 0.33 # model…...

mysql 更改密码
由于两台设备的mysql数据库的密码不一样,开发时每次连接数据库都需要更改配置文件,所以想修改一下mysql数据库的密码。 mysql 修改密码千万不要直接修改,直接修改的话会出现两种情况: 1,修改成功,无法登录。…...

Android YUV存储方式
排名 性能:YUV444 > YUV422 > YUV420 > YUV411 YUV444:YUV444 提供最高质量的色彩准确性和图像细节,但需要更多的存储空间和传输带宽。适用于对图像质量要求很高的应用,如专业视频编辑或高端图像处理。YUV422࿱…...
SSM家具个性定制管理系统开发mysql数据库web结构java编程计算机网页源码eclipse项目
一、源码特点 SSM 家具个性定制管理系统是一套完善的信息系统,结合springMVC框架完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码和数据库,系统主要采用…...

来自Microsoft Teams的摄像头背景图片
原文件在👆,下面是预览图 如果你安装了Microsoft Teams也可以搜索MSTeams,就在MSTeams/Backgrounds...
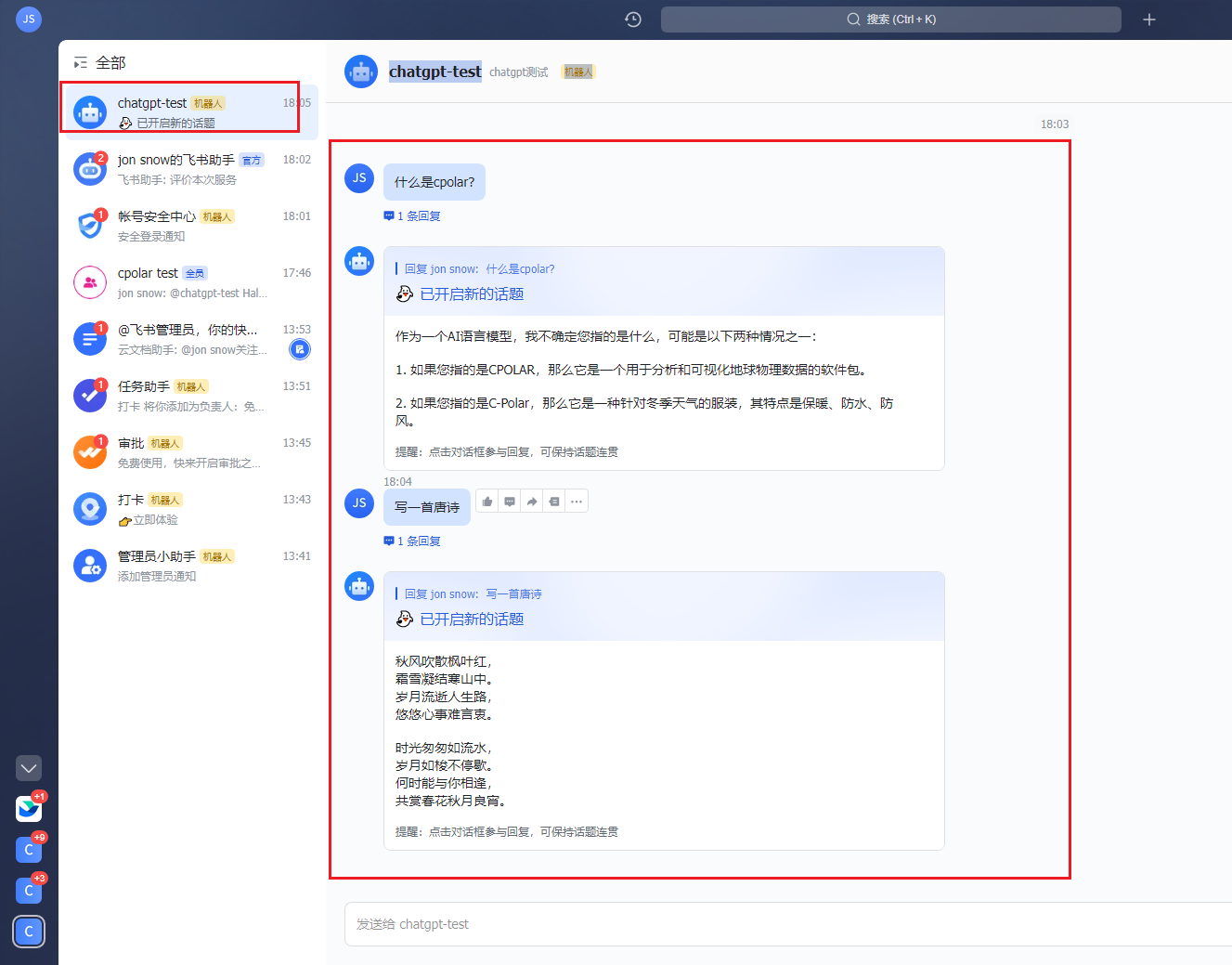
飞书如何接入ChatGPT-打造个人智能问答助手实现无障碍交流
目录 前言 环境列表 1.飞书设置 2.克隆feishu-chatgpt项目 3.配置config.yaml文件 4.运行feishu-chatgpt项目 5.安装cpolar内网穿透 6.固定公网地址 7.机器人权限配置 8.创建版本 9.创建测试企业 10. 机器人测试 总结 前言 在飞书中创建chatGPT机器人并且对话&am…...
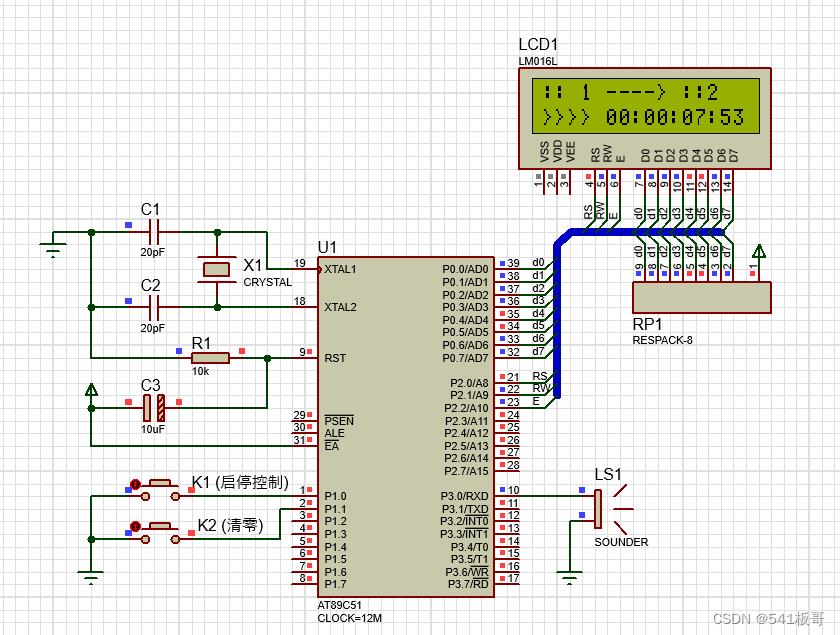
Proteus仿真--基于1602LCD的秒表设计
本文介绍基于1602LCD的秒表设计(完整仿真源文件及代码见文末链接) 仿真图如下 本设计中80C51单片机作为主控,用1602LCD作为显示模块,共有2个按键,K1按键用于秒表计时启停控制,K2用于清零显示内容 仿真运…...

香港站群服务器中1C/2C/4C/8C 的概念及区别
在选择香港站群服务器时,经常会看到1C、2C、4C和8C等不同的IP段。这些IP段代表了不同的子网掩码长度,也反映了服务器的IP地址数量和丰富性。 让我们来了解一下什么是IP段。IP段是指一组连续的IP地址,其中每个地址的前三个数字相同&…...
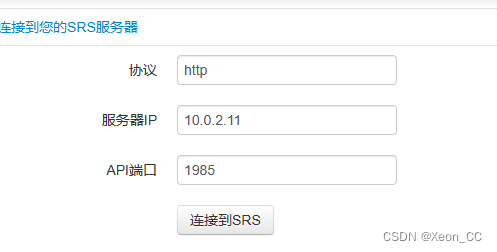
搭建SRS视频服务器
去官方网站下载FFmpeg6.1 https://ffmpeg.org/download.html拷贝到CentOS7.9中的/opt目录下,解压并重命名 tar -xvf ffmpeg-6.1.tar.xz 解压后编译安装 ./configure make make install从github下载SRS4.0release 解压后 如果ffmpeg的路径不在/usr/local/bin/ffmpe…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
