python树长子兄弟链存储结构(孩子兄弟链存储结构)
长子兄弟链存储结构(孩子兄弟链存储结构)解释:
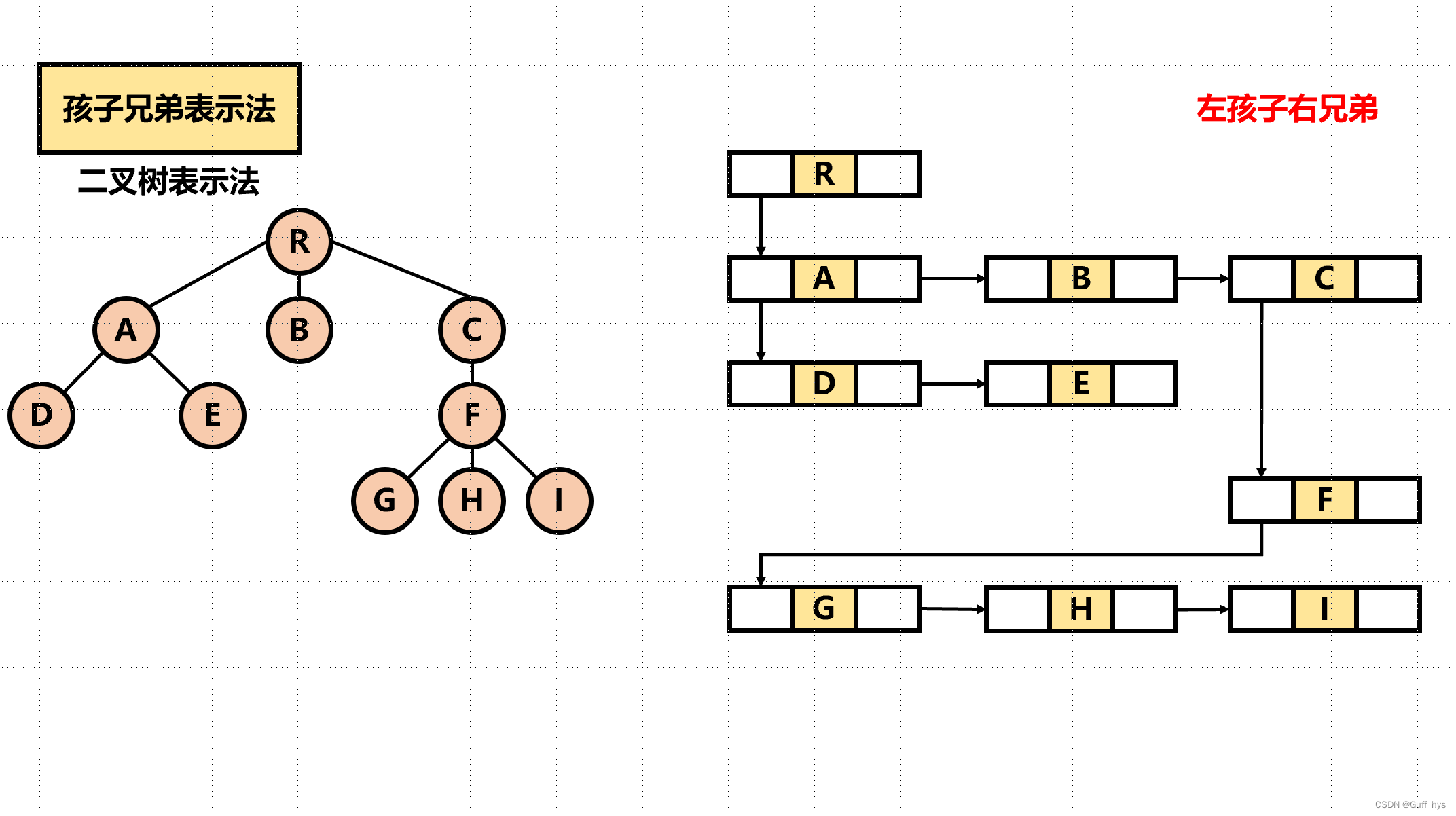
长子兄弟链存储结构是一种树的存储结构,它使用孩子兄弟表示法(也称作左孩子右兄弟表示法)来表示树的结构。这种表示方法主要用于存储一般的树,而不是二叉树。
在长子兄弟链存储结构中,树中的每个节点都有两个指针:一个指向它的第一个孩子节点,另一个指向它的右边(兄弟)的节点。这种表示方法使用了类似链表的结构,使得树的每个节点可以灵活地连接到它的子节点和兄弟节点。
使用长子兄弟链存储结构,可以有效地表示任意形状的树,而且在进行树的遍历和操作时也相对容易。这种存储结构的主要优点是节省空间,因为不需要额外的指针来表示左右子树,同时也便于实现树的各种操作,如插入、删除和查找等。长子兄弟链存储结构在树的应用中具有一定的灵活性和效率。
代码:
class BENode():def __init__(self,data,son=None,brother=None):self.data=dataself.son=sonself.brother=brotherclass BEStree():def __init__(self):self.data=[]# 建立根节点,并存储在self.data中def create_t(self,e):a = BENode(e)self.data.append(a)# 建立节点与节点之间关系,并存储在self.data中,brother的存储优先级<son的存储优先级(增加节点)def create_other(self,i,son=None,brother=None):#i为节点的下标if son!=None:s = BENode(son)self.data.append(s)self.data[i].son = sif brother!=None:b = BENode(brother)self.data.append(b)self.data[i].brother=b# 删除节点值def delx(self,e):for i in range(len(self.data)):# 从节点属性删除节点值if self.data[i].brother != None:if self.data[i].brother.data==e:self.data[i].brother.data=Nonebreakif self.data[i].son != None:if self.data[i].son.data==e:self.data[i].son.data=Nonebreakfor i in range(len(self.data)):# 从存储结构删除if self.data[i].data==e:self.data[i].data=Nonebreak#修改节点值,将e修改为n_edef change(self,e,n_e):for i in range(len(self.data)):# 从节点属性修改节点值if self.data[i].brother!=None:if self.data[i].brother.data==e:self.data[i].brother.data=n_ebreakif self.data[i].son != None:if self.data[i].son.data==e:# 从存储结构修改self.data[i].son.data=n_ebreakfor i in range(len(self.data)):if self.data[i].data==e:self.data[i].data=n_ebreak# 查询节点值,返回节点def find(self,e):for i in range(len(self.data)):if self.data[i].data==e:return self.data[i]#先序遍历,传入的t的参数为self.data[0]def display_f(self,t):if t!=None:print(t.data,end=' ')self.display_f(t.son)self.display_f(t.brother)#后序遍历def display_t(self,t):if t!=None:self.display_t(t.son)self.display_t(t.brother)print(t.data,end=' ')#中序遍历def display_m(self,t):if t!=None:self.display_m(t.son)print(t.data,end=' ')self.display_m(t.brother)a = BEStree()
a.create_t('A')
a.create_other(0,'B')
a.create_other(1,'D','C')
a.create_other(2,'G')
a.create_other(3,'E')
a.create_other(5,None,'F')
#后序遍历
a.display_t(a.data[0])
print()
#中序遍历
a.display_m(a.data[0])
print()
#先序遍历
a.display_f(a.data[0])
print()
# 改变值
a.change('A',"10")
a.display_f(a.data[0])
print()
# 删除值
a.delx('10')
a.display_f(a.data[0])长子兄弟链存储结构的优点:
1. 节省空间:相比于其他树的存储结构,长子兄弟链存储结构更加节省空间,因为它不需要额外的指针来表示左右子树。
2. 灵活性:长子兄弟链存储结构可以有效地表示任意形状的树,包括多叉树和不规则树,因此具有较强的灵活性。
3. 操作便利:在长子兄弟链存储结构中,树的节点之间使用指针连接,这样可以方便地进行树的遍历、插入、删除和查找等操作。
长子兄弟链存储结构的缺点:
1. 操作复杂性:相对于其他树的存储结构,长子兄弟链存储结构的操作可能会更加复杂,因为需要考虑节点之间的兄弟关系和孩子关系。
2. 不适用于特定场景:长子兄弟链存储结构主要适用于一般的树结构,对于特定的树,如二叉树或平衡树等,可能不是最佳的选择。
3. 不适合频繁修改的树:长子兄弟链存储结构对于频繁进行插入和删除操作的树可能不太适用,因为这样的操作可能会导致链的频繁调整,影响效率。

相关文章:

python树长子兄弟链存储结构(孩子兄弟链存储结构)
长子兄弟链存储结构(孩子兄弟链存储结构)解释: 长子兄弟链存储结构是一种树的存储结构,它使用孩子兄弟表示法(也称作左孩子右兄弟表示法)来表示树的结构。这种表示方法主要用于存储一般的树,而不…...

开源和闭源软件对开发的影响
开源软件的优势: 开源性:开源软件允许任何人查看、修改和发布源代码,这促进了代码的共享和集体学习。透明性:开源软件提高了软件的透明度,使用户可以更好地理解软件的工作原理,增加对软件的信任。社区支持…...

centos无法进入系统之原因解决办法集合
前言 可爱的小伙伴们,由于精力有限,暂时整理了两类。如果没有你遇到的问题也没有关系,欢迎底下留言评论或私信,小编看到后第一时间帮助解决 一. Centos 7 LVM xfs文件系统修复 情况1: [sda] Assuming drive cache:…...

【Linux】系统初始化配置
CentOS 7 的虚拟机安装后必须要做的几个操作,记录以下,网络配置修改、yum源安装、基础工具安装: 1、先修改权限,新建普通用户,并授权普通用户apps 的sudo权限; useradd apps password apps visudo apps A…...
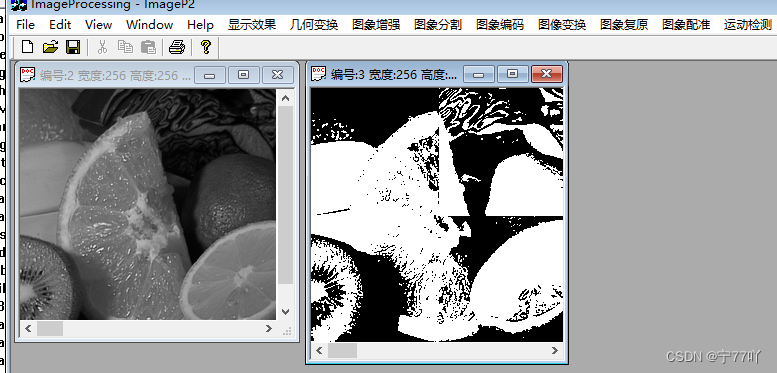
使用VC++设计程序对一幅256级灰度图像进行全局固定阈值分割、自适应阈值分割
图像分割–全局固定阈值分割、自适应阈值分割 获取源工程可访问gitee可在此工程的基础上进行学习。 该工程的其他文章: 01- 一元熵值、二维熵值 02- 图像平移变换,图像缩放、图像裁剪、图像对角线镜像以及图像的旋转 03-邻域平均平滑算法、中值滤波算法、…...

【ArcGIS Pro微课1000例】0035:栅格影像拼接(dem高程数据)
本实验讲解在ArcGIS Pro中,栅格数据的两种拼接(镶嵌)方法,适用于遥感影像、DOM、DEM、DSM等常见栅格数据。 文章目录 一、加载实验数据二、栅格拼接工具1. 镶嵌2. 镶嵌至新栅格三、注意事项四、拓展阅读一、加载实验数据 加载配套实验数据中的0035.rar中的两个dem数据,如…...

Zynq-7000系列FPGA使用 Video Processing Subsystem 实现图像缩放,提供工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐FPGA图像处理方案FPGA图像缩放方案自己写的HLS图像缩放方案 3、设计思路详解Video Processing Subsystem 介绍 4、工程代码详解PL 端 FPGA 逻辑设计PS 端 SDK 软件设计 5、工程移植说明vivado版本不一致处理FPGA型号不一致处理其他注意事项…...
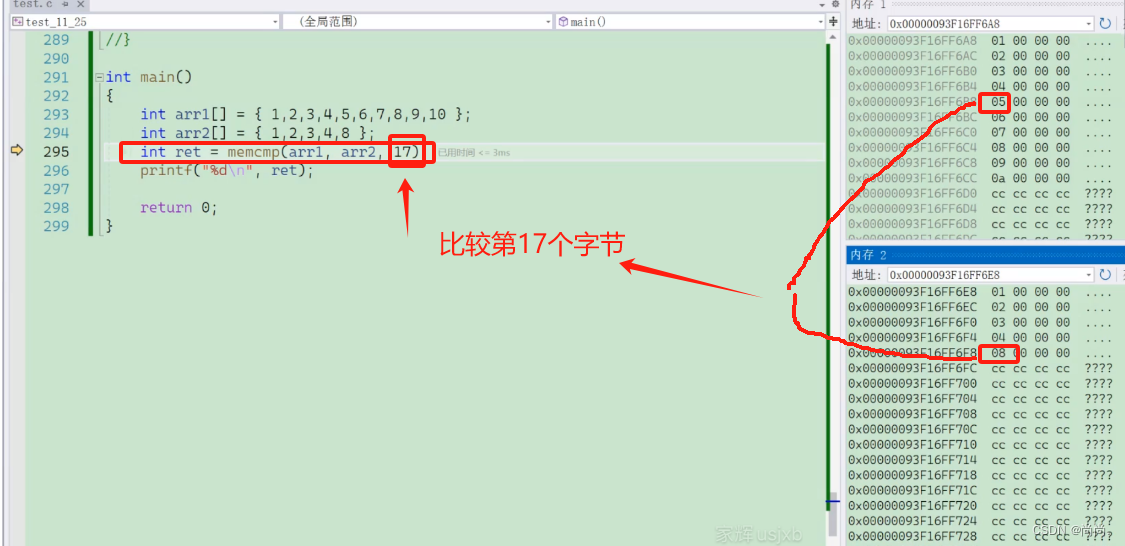
【C】内存函数
目录 1. memcpy 使用和模拟实现 2. memmove 使⽤和模拟实现 3. memset 函数的使用 4. memcmp 函数的使用 1. memcpy 使用和模拟实现 void * memcpy ( void * destination, const void * source, size_t num ); • 函数memcpy从source的位置开始向后复制num个字节的数据到d…...

windows系统玩游戏找不到d3dx9_35.dll缺失的解决方法
分享一个我们在打开游戏或许软件过程中遇到的问题——“由于找不到d3dx9_35.dll,无法继续执行代码”的五个修复方案。这个问题可能会影响到我们的工作和娱乐效率,甚至可能导致工作的延期。因此,我希望通过今天的文章,能够帮助大家更好地解决这…...
webshell之内置函数免杀
原始webshell 查杀的点在于Runtime.getRuntime().exec非常明显的特征 利用ProcessBuilder替换Runtime.getRuntime().exec(cmd) Runtime.getRuntime().exec(cmd)其实最终调用的是ProcessBuilder这个函数,因此我们可以直接利用ProcessBuilder来替换Runtime.getRunti…...
)
react高阶成分(HOC)
使用React函数式组件写了一个身份验证的一个功能,示例通过高阶组件实现的一个效果展示: import React, { useState, useEffect } from react;// 定义一个高阶组件,它接受一个组件作为输入,并返回一个新的包装组件 const withAuth…...
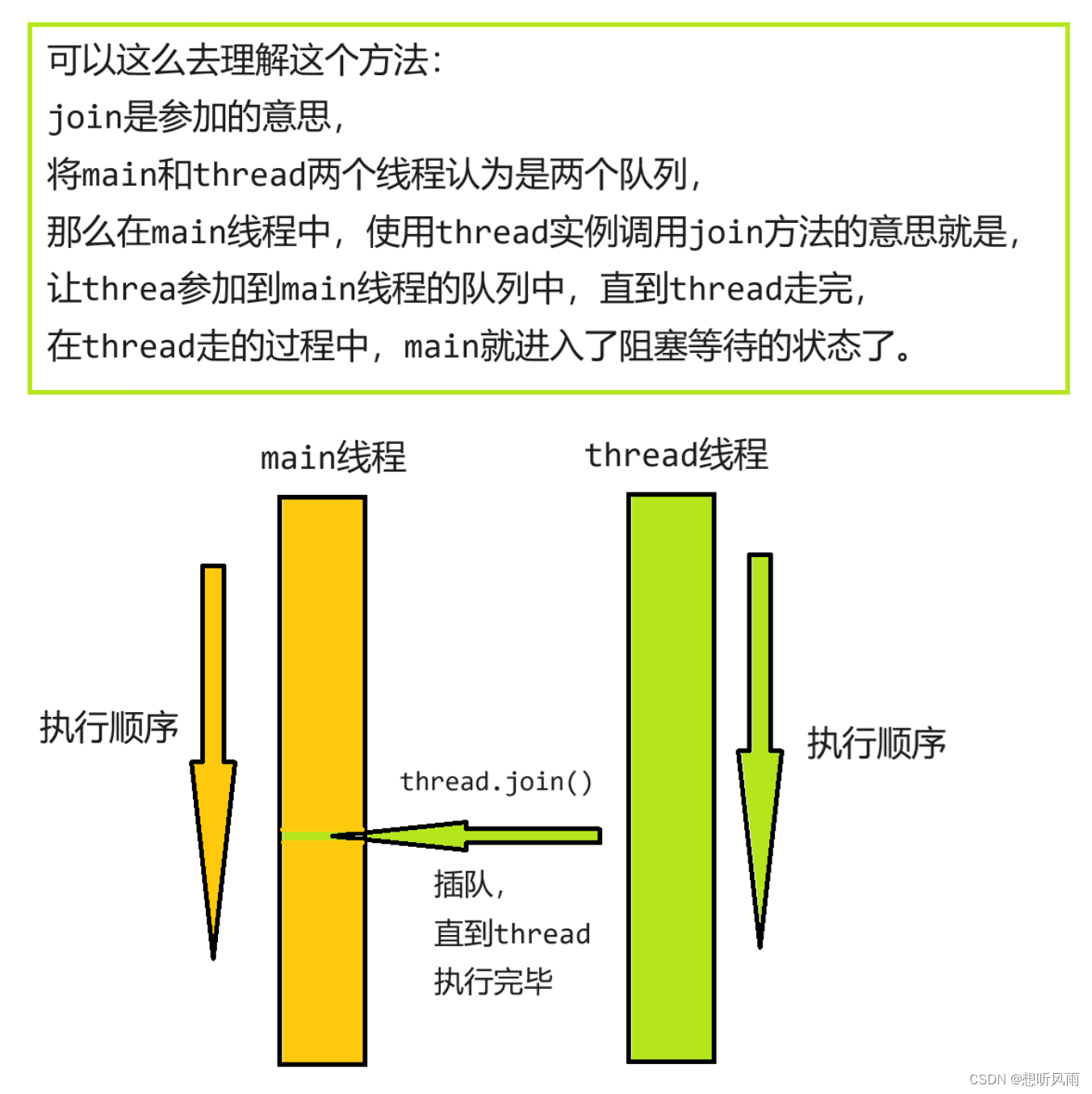
<JavaEE> Thread线程类 和 Thread的常用方法
目录 一、Thread概述 二、构造方法 三、常用方法 1.1 getId()、getName()、getState()、getPririty() 1.2 start() 1.3 isDaemon()、setDaemon() 1.4 isAlive() 1.5 currentThread() 1.6 Interrupt()、interrupted()、isInterrupted() 1.6.1 方法一:添加共…...

Linux加强篇004-Vim编辑器与Shell命令脚本
目录 前言 1. Vim文本编辑器 1.1 编写简单文档 1.2 配置主机名称 1.3 配置网卡信息 1.4 配置软件仓库 2. 编写Shell脚本 2.1 编写简单的脚本 2.2 接收用户的参数 2.3 判断用户的参数 3. 流程控制语句 3.1 if条件测试语句 3.2 for条件循环语句 3.3 while条件循环语…...

【shell脚本】常见的shell脚本面试题目
1、请用shell脚本for,while,until这三种方式写出输出1到100的所有偶数的方法。 sum=0;for((i=0;i<=100;i+=2));do let sum+=i;done;echo $sum sum=0;i=0;while [ $i -le 100 ];do let sum+=i;let i+=2;done;echo $sum sum=0;i=0;until [ $i -gt 100 ];do let sum+=i;let i+…...
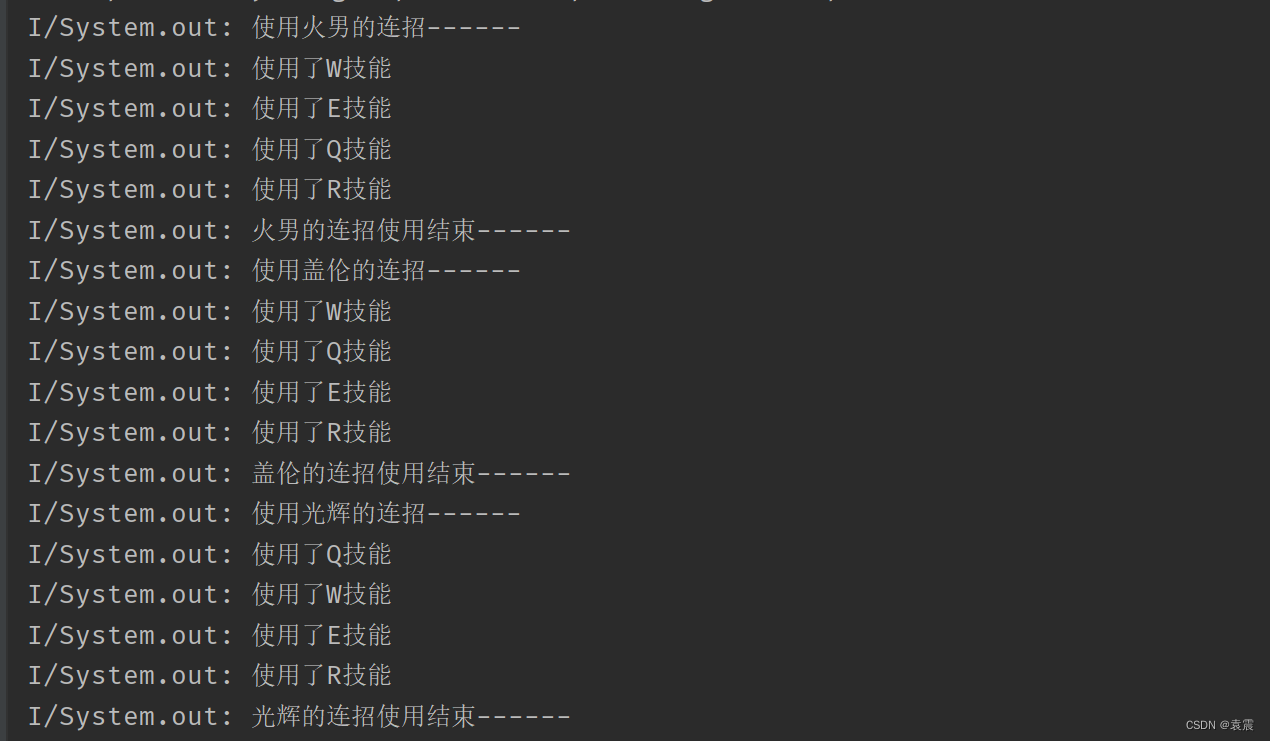
Android设计模式--外观模式
弈之为术,在人自悟 一,定义 外观模式要求一个子系统的外部与其内部的通信必须通过一个统一的对象进行。提供一个高层次的接口,使得子系统更易于使用。 外观模式在开发中的使用频率是非常高的,尤其是在第三方的SDK里面࿰…...
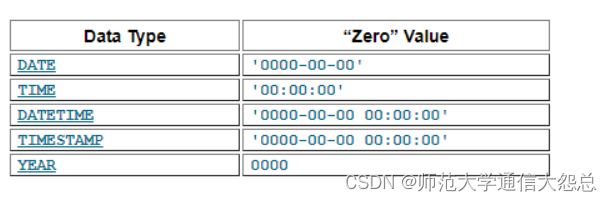
03_MySQL基本SQL语句讲解
#课程目标 能够创建、删除数据表能够对表里的数据记录进行增加、删除、修改、查询操作能够创建、删除用户能够给用户授权并回收权限了解delete和truncate语句的区别 #一、数据库基本操作 ##1、查看数据库相关信息 mysql> show databases; 查看所有数据库 mysql>…...

【C语法学习】28 - 字符测试函数
文章目录 1 isalnum()函数2 isalpha()函数3 islower()函数4 isupper()函数5 isdigit()函数6 isxdigit()函数7 iscntrl()函数8 isgraph()函数9 isspace()函数10 isblank()函数11 isprint()函数12 ispunct()函数13 tolower()函数14 toupper()函数 1 isalnum()函数 isalnum()函数…...
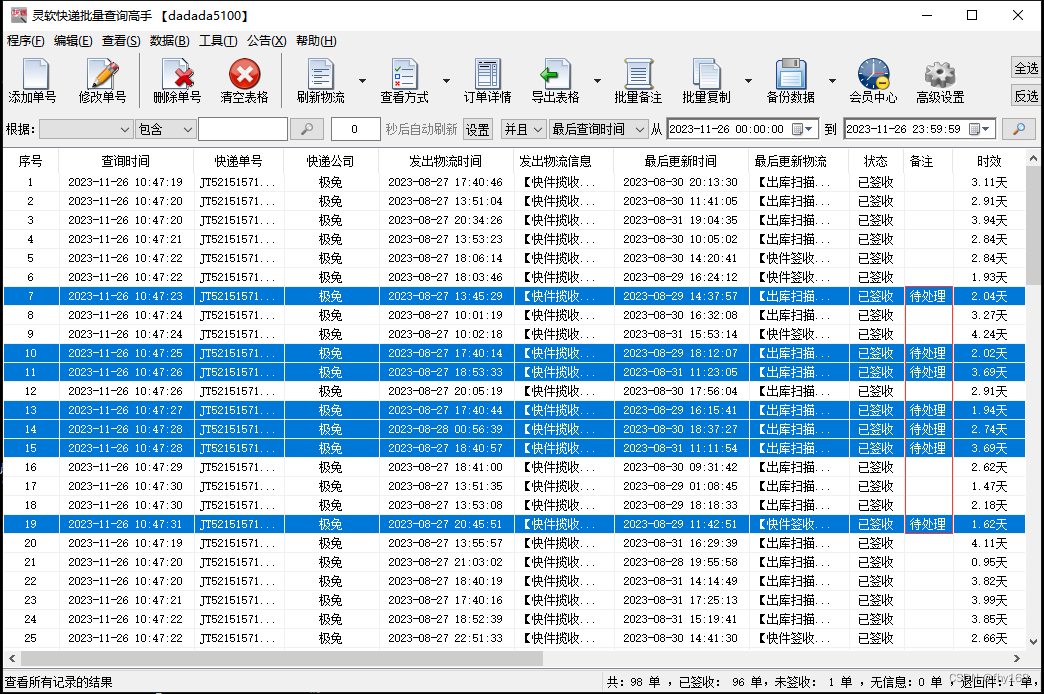
极兔快递查询,极兔快递单号查询,对需要的单号记录进行备注
批量查询极兔快递单号的物流信息,对需要的快递单号记录进行备注。 所需工具: 一个【快递批量查询高手】软件 极兔快递单号若干 操作步骤: 步骤1:运行【快递批量查询高手】软件,并登录 步骤2:点击主界面左…...

树的序列化与反序列化
1 序列化与反序列化 二叉树的序列化与反序列化 1.1 实现思路 方式一:前序遍历 通过前序遍历方式实现二叉树的序列化将结果存入队列中要注意空节点也要存null 方式二:层序遍历 层序遍历也是用队列实现注意从左到右,遇到空节点存null 1.2 …...
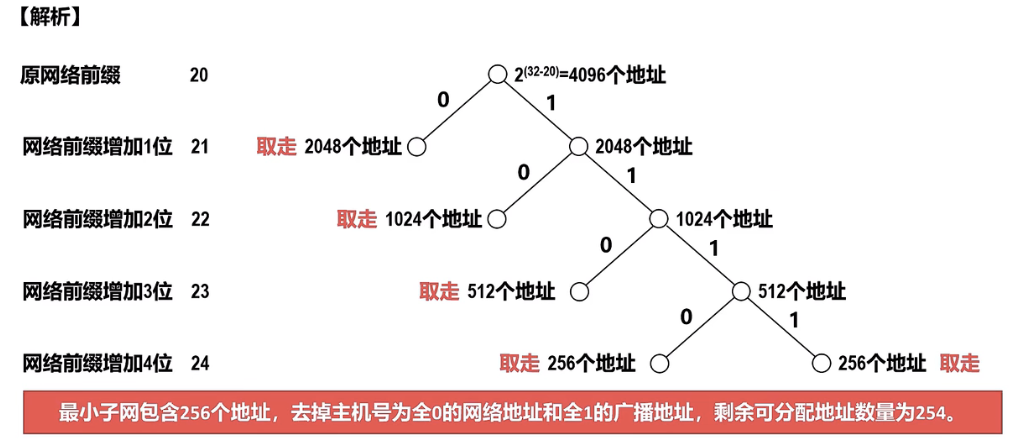
定长子网划分和变长子网划分问题_二叉树解法_通俗易懂_配考研真题
引入:定长子网划分和变长子网划分的基本概念 定长子网划分和变长子网划分的基本概念 目前常用的子网划分,是基于CIDR的子网划分,也就是将给定的CIDR地址块划分为若干个较小的CIDR地址块。 定长子网划分: 使用同一个子网掩码来划分子网,因…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
