『OPEN3D』1.8 点云的配准理论
点云的配准是将不同的3D点云对齐成一个完成的点云模型;配准的目标是找到两帧点云之间的相对旋转(rotation)与平移(translation),使得两份点云中有重叠的区域能够完好拼接。
点云配准示例图(来自PCL)

上图为初始的5份点云数据,需要将着几份点云数据拼接成如下图中完整的模型

点云动态配准示例

常见的点云配准方式主要包含ICP配准以及NDT配准以及他们的配准,当然还包括神经网络的点云配准方式。
1、点云配准理论
点云配准需要找到两份点云数据之间点的对应估计,也就是找到两份点云中重叠的部分才可以进行配准,这类配准,对于有确定对应点的配准拥有闭式解(closed form solution)不需要迭代求解即可获取最优值。
对应点的寻找方式:
1 若为深度相机,则可以借助图像信息来寻找对应的匹配点并投影回3d空间
2 若为两帧点云信息,则可以借助点云特征点来进行确立
不过上诉方法都会出现误匹配,一般会借助RANSAC(随机采样一致性)来得到更为robust的估计。
1 ICP主要为point2point ICP和point2plane两种ICP方式
ICP配准点云时需要有较为准确的初始位姿后再使用该方法进行精配准;ICP的点云配准大体步骤分为如下几步:
1 点的匹配(可以从图像中来或者点云中来)
1.1 在两帧点云中找到对应的关键点,点云中的关键点一般为特定的几何结构,比如书本的边角,与图像类似;点云中的关键点包括NARF;SIFT;FAST;当然也可以不适用关键点;使用每一个点或者点云中的一部分点来进行配准;不过那样的话会导致计算量过大。
1.2 特征的描述子;与图像类似,再找到点云的关键点后,需要提取该关键点的描述子信息;通过组合该结构的信息来生成对应的向量用于比对;点云的中描述子包括NARF;FPFH;BRIEF;SIFT等。
2 匹配点估计;给定两帧点云的特征向量集合;通过关键点与描述子来找到重叠区域中相互对应的关键点:对于关键点或特征的匹配,可以使用暴力搜索;kd-tree(FLANN)等方式来进行匹配
3 匹配点对估计;类似与图像中关键点匹配;点云中的关键点匹配也存在许多误匹配;误匹配会影响最终的配准结果;因此此处可以使用ransac或者根据匹配点对的百分位进行截取等方式来进行优化;如果一帧中的某个关键点与另一帧中的多个关键点匹配;则会取最小距离来确定匹配点
4 变换矩阵计算;再得到准确的相互匹配的点云后;则可以计算变换矩阵;
其中point2point的评估误差为
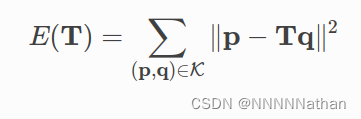
point2plane的评估误差为(其中np为点P的法线信息)
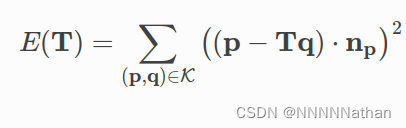
估计两个点集的R和t可以使用使用SVD或者非线性优化求解;
1 SVD方法
给定两对匹配点的点集和
,对其中第i对匹配点的误差项为:
因此可以对所有点构建最小二乘问题,求得使误差平方和达到极小的R和t:
分别定义两组点的质心为(此处使用不带下标的项来代表质心):
在误差函数中进行展开
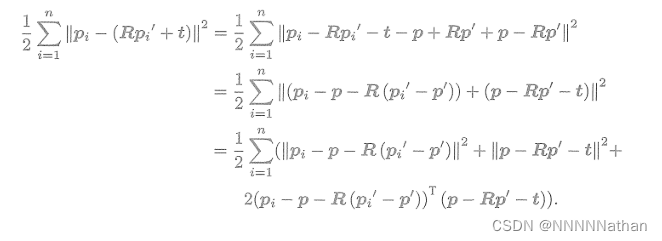
展开后最后一项元素求和为0(所有元素相加减去n个
的质心
为0),因此优化的结果仅与前两项相关,即
上式中,只有左边和旋转矩阵R相关,右侧同时R与t。因此只要求得R后令右式为0即可求出t。
ICP的SVD方法流程如下
1、计算两组匹配点的质心与
, 然后将每个点减去质心得到去质心的坐标:
2、根据上述阐述的优化,计算旋转矩阵:
3、根据计算得到的旋转矩阵计算平移向量t
因此,按照上面的步骤,要先求取两组点集之间的旋转矩阵,所以下面说重点一下R的计算:
其中第一项与R无关;第二项
中因为R为正交矩阵因此
,也与R无关;只有最后一项的
与R有关,因此有如下推导:
注: 其中为trace(迹),有
然后可以使用SVD分解得出最优的旋转矩阵R。
可知W是一个n*n的矩阵,n为点集的维度,若是点云数据则n=3则W是3*3的矩阵,
若此时W是可逆矩阵,则可以直接通过公式获得最优的旋转矩阵
但考虑到所有情况,直接对W进行SVD分解也是可以的:
其中为奇异值组成的对角矩阵,对角线元素从大到小排列,UV则为正交矩阵;当W满秩时,R为
若R的行列式为负数,则去-R为最优数值。
对这块刚兴趣的同学可以参考Kabsch算法的实现
https://en.wikipedia.org/wiki/Kabsch_algorithm![]() https://en.wikipedia.org/wiki/Kabsch_algorithm
https://en.wikipedia.org/wiki/Kabsch_algorithm
2 非线性优化
2 open3d中使用ICP
更新中
相关文章:
『OPEN3D』1.8 点云的配准理论
点云的配准是将不同的3D点云对齐成一个完成的点云模型;配准的目标是找到两帧点云之间的相对旋转(rotation)与平移(translation),使得两份点云中有重叠的区域能够完好拼接。 点云配准示例图(来自…...

Python数据结构
目录 5.1. 列表详解 5.1.1. 用列表实现堆栈 5.1.2. 用列表实现队列 5.1.3. 列表推导式 5.1.4. 嵌套的列表推导式 5.2. del 语句 5.3. 元组和序列 5.4. 集合 5.5. 字典 5.6. 循环的技巧 5.7. 深入条件控制 5.8. 序列和其他类型的比较 本章深入讲解之前学过的一些内容…...

突发!新华三总裁《致全体员工的一封信》,中高层全面降薪10%-20%!
* 你好,我是前端队长,在职场,玩副业,文末有福利! 精彩回顾:进了央企,拿了户口,却感觉被困住了。 11月23号,某社交平台爆出了新华三总裁于英涛的《致全体员工的一封信》&a…...

QIIME 2介绍
QIIME 2(Quantitative Insights Into Microbial Ecology 2)是一个用于分析和解释微生物组数据的开源生物信息学工具。它是QIIME的第二个版本,经过重新设计以提高灵活性、可扩展性和可重复性。 1. 关于QIIME 2的一些重要特征和概念࿱…...

Spring Cloud Gateway 的简单介绍和基本使用
前言 本文主要对Spring Cloud Gateway进行简单的概念介绍,并通过多模块编程的方式进行一个简单的实操。 文章目录 前言1 什么是网关(概念)2 微服务中的网关2.1 问题12.2 问题2 3 网关作用4 Spring Cloud Gateway组成5 Spring Cloud Gateway基…...
Leaflet结合Echarts实现迁徙图
效果图如下: <!DOCTYPE html> <html><head><title>Leaflet结合Echarts4实现迁徙图</title><meta charset"utf-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0">…...

在mysql存储过程中间部分,使用游标遍历动态结果集(游标动态传参使用)
mysql游标动态传参实现(动态游标) 1.问题2.需求描述3.实现3.1.使用3.2.代码(直接看这都可以) 1.问题 众所周知,mysql存储过程功能是没有oracle的包功能强大的,但是在去O的趋势下,mysql存储过程的…...
全球SAR卫星大盘点与回波数据处理专栏目录
近年来,随着商业航天的蓬勃发展,商业SAR卫星星座成为美欧等主要航天国家的发展重点,目前已在全球范围内涌现出众多初创公司进军商业SAR领域,开始构建大规模商业微小SAR卫星星座,其所具有的创新服务能力将为传统的商业遥…...

C语言重点编程题——21-30
目录 21. 从键盘输入的10个整数中,找出第一个能被7整除的数。若找到,打印此数后退出循环;若未找到,打印"not exist" ★★★★22.有一个一维数组,内放10个学生成绩,写一个函数,求出平均分。 23.有N个学生,每个学生的信息包括学号、 性别、姓名、四门课的成绩…...

pip install 使用清华镜像源
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple some-package 官方文档: pypi | 镜像站使用帮助 | 清华大学开源软件镜像站 | Tsinghua Open Source Mirror...

VBA技术资料MF86:将PPT文件批量另存为PDF文件
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套,分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的入门,到…...
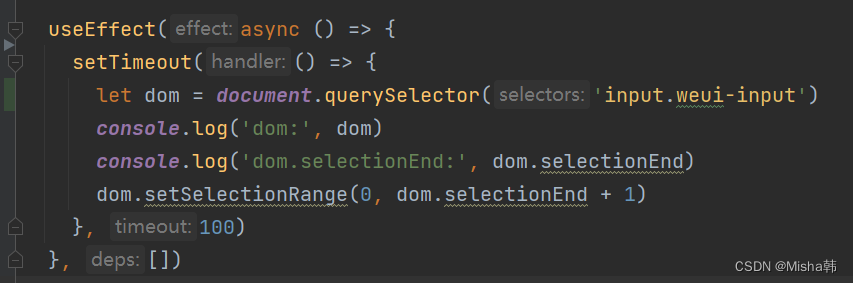
taro h5 ios解决input不能自动获取焦点拉起键盘
描述:页面中有个按钮,点击跳转到第二个页面(有input),能直接获取焦点拉起键盘输入 安卓: 直接用focus() ios: focus无效,必须手动拉起 原理: 点击按钮的时候拉起一…...
「Docker」如何在苹果电脑上构建简单的Go云原生程序「MacOS」
介绍 使用Docker开发Golang云原生应用程序,使用Golang服务和Redis服务 注:写得很详细 为方便我的朋友可以看懂 环境部署 确保已经安装Go、docker等基础配置 官网下载链接直达:Docker官网下载 Go官网下载 操作步骤 第一步 创建一个…...

Vue环境的搭建
1.Vue开发的两种方式 (1)核心包传统开发模式 基于html/css/js文件,直接引入,开发Vue。 (2)工程化开发模式(更常用的一种): 主要是基于构建工具(例如,webp…...
在Spring Boot中实现单文件,多文件上传
这篇文章算是一篇水文,因为也没啥好讲的,在Spring Boot中,上传文件是我们常常做的,包括我们在实际开发过程中,我们也经常碰到与文件上传有关的功能,这也算是我们常用的一个功能了,毕竟作为开发者…...
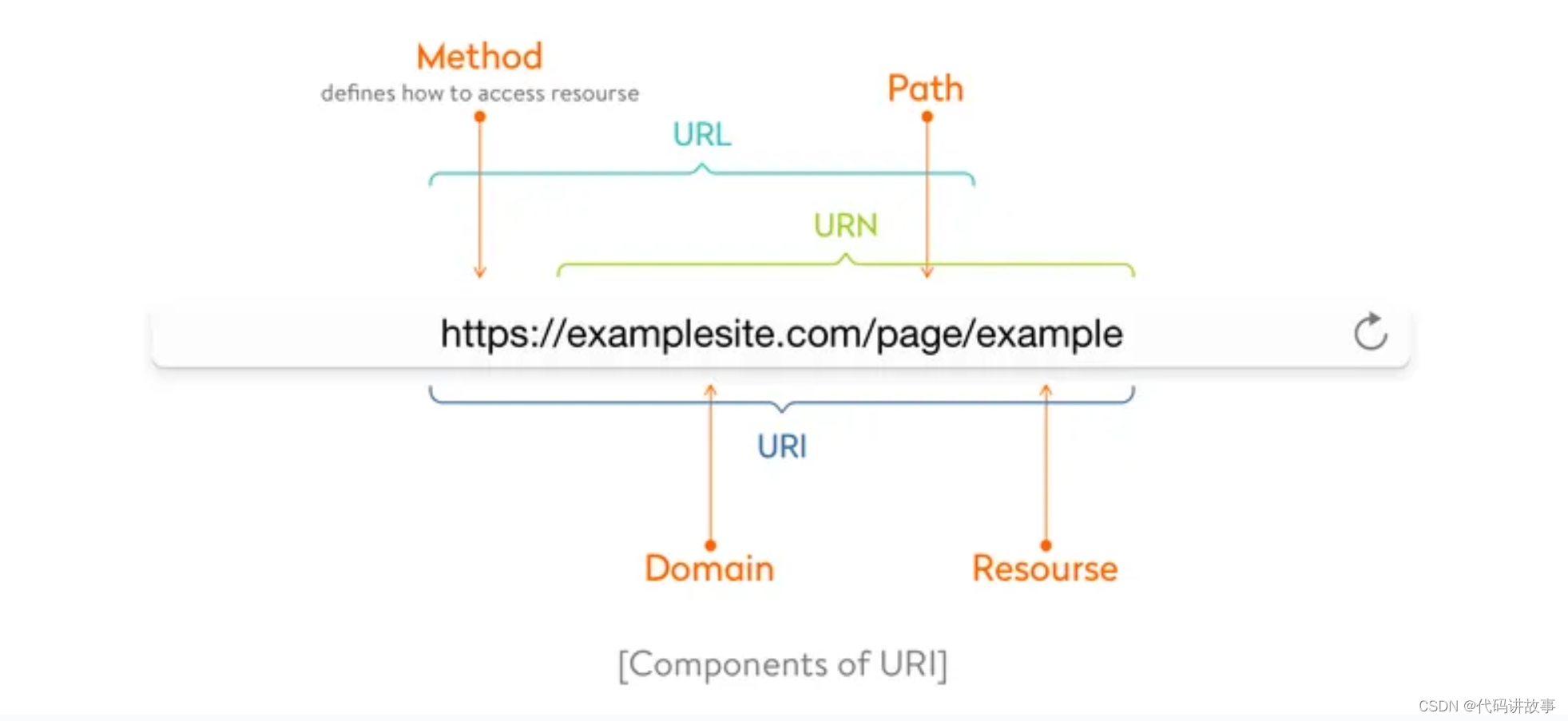
如何在 Web 应用程序中查找端点?
如何在 Web 应用程序中查找端点? 这篇文章主要讲述了如何在网络应用中找到端点。以下是文章的主要要点: 端点是网络服务的访问地址,通过引用这个URL,客户可以访问服务提供的操作。端点提供了寻址Web服务端点所需的信息。 HTTP消息是服务器和客户端之间交换数据的方式,包…...

使用el-scrollbar实现定位滚动,以及el-scrollbar去掉横向滚动条
实现滚动 <el-scrollbar ref"scroll" style"height: 100%;">// ... </el-scrollbar>可以使用如下属性: 想要滚动到哪个指定位置,自己获取或计算 this.$refs[scroll].wrap.scrollTop 0 //想滚到哪个高度,…...
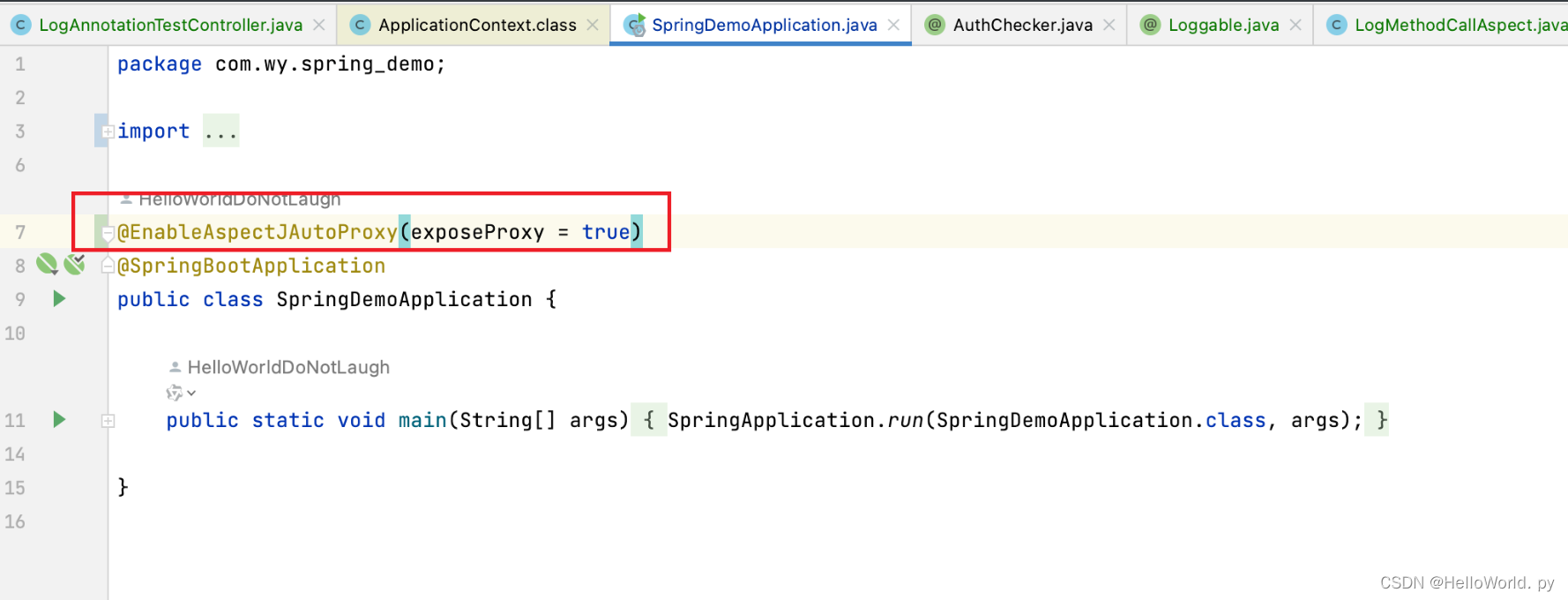
AOP + 自定义注解实现日志打印
1. 先定义个注解,让它作用于方法上 Target({ElementType.METHOD}) Retention(RetentionPolicy.RUNTIME) public interface Loggable {}2. 定义切面 Aspect Component Slf4j public class LogMethodCallAspect {Pointcut("annotation(com.wy.spring_demo.aop.…...

美团YOLOv6量化部署实战方案
文章目录 1. 背景和难点2. 量化方案实战2.1 重参数化优化器2.1.1 RepOpt2.1.2 RepOpt 版本的 PTQ2.1.3 RepOpt 版本的 QAT2.2 基于量化敏感度分析的部分量化2.3 基于通道蒸馏的量化感知训练2.3.1 通道蒸馏2.3.2 YOLOv6 量化感知蒸馏框架3. 部署时优化3.1 图优化3.1.1 性能分析3…...
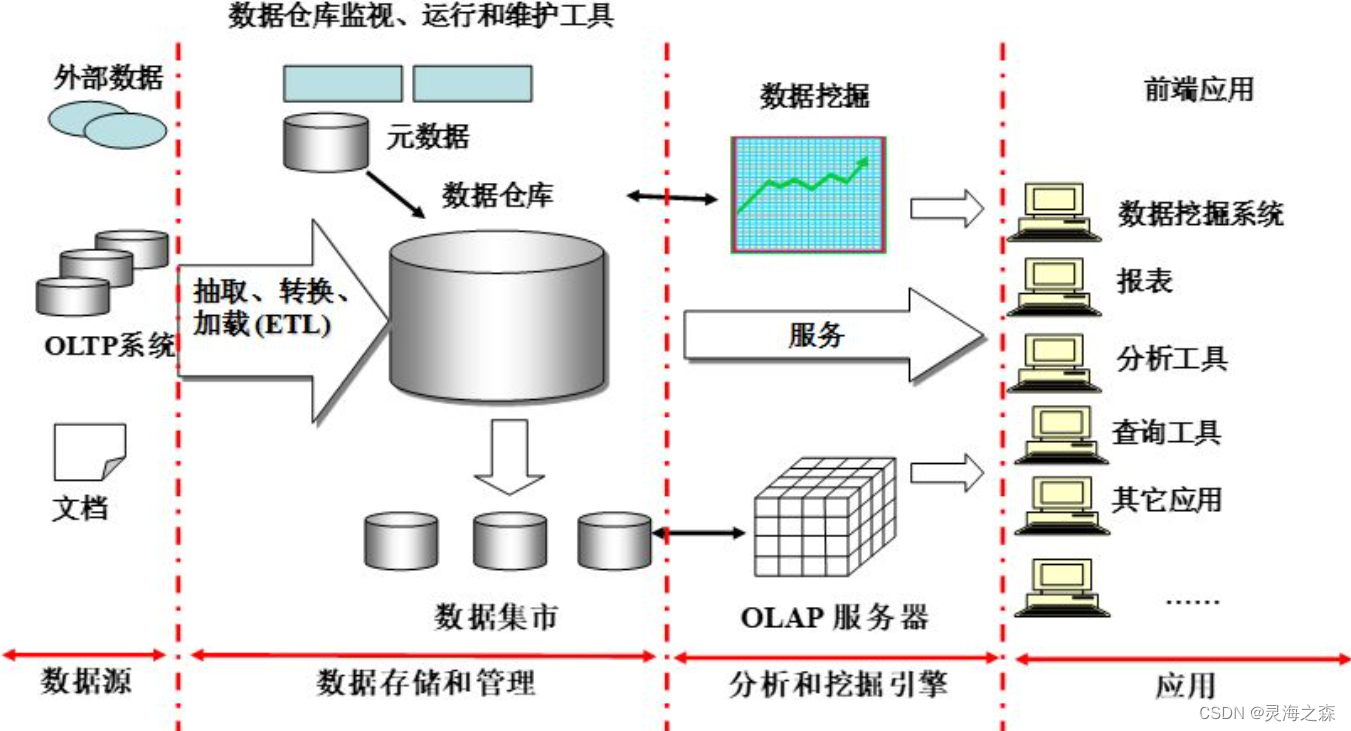
hive杂谈
数据仓库是一个面向主题的、集成的、非易失的、随时间变化的,用来支持管理人员决策的数据集合,数据仓库中包含了粒度化的企业数据。 数据仓库的主要特征是:主题性、集成性、非易失性、时变性。 数据仓库的体系结构通常包含4个层次ÿ…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
