[Matlab有限元分析] 2.杆单元有限元分析
1. 一维杆单元有限元分析程序
一维刚单元的局部坐标系(单元坐标系)与全局坐标系相同。
1.1 线性杆单元
如图所示是一个杆单元,由两个节点i和j,局部坐标系的X轴沿着杆的方向,由i节点指向j节点,每个节点有一个自由度,在使用时需要定义杆长L、截面积A和弹性模型E。

单元刚度矩阵为:
线性杆单元有限元分析MATLAB程序主要包括单元刚度矩阵(Bar1D2Node_Stiffness)、单元组装(Bar1D2Node_Assembly)、单元应力(Bar1D2Node_Stress)和节点力(Bar1D2Node_Forces)四个函数,分别如下:
function k = Bar1D2Node_Stiffness(E,A,L)
% 该函数计算线性杆单元的刚度矩阵
% 输入:弹性模量E,杆的横截面积A和长度L
% 输出:单元刚度矩阵k(2*2)
k = [E*A/L -E*A/L ; -E*A/L E*A/L];function y = Bar1D2Node_Assemble(K,k,i,j)
% 该函数进行单元刚度矩阵的组装
% 输入:单元刚度矩阵k和单元节点编号i,j
% 输出:整体刚度矩阵K
DOF(1) = i;
DOF(2) = j;
for n1 = 1:2for n2 = 1:2K(DOF(n1),DOF(n2)) = K(DOF(n1),DOF(n2))+k(n1,n2);end
end
y = K;function forces = Bar1D2Node_Forces(k,u)
% 该函数计算线性杆单元的节点力
% 输入:单元刚度矩阵k,单元的位移列阵u(2*1)
% 输出:单元节点力forces
forces = k*u;function stress = Bar1D2Node_Stress(k,u,A)
% 该函数计算线性杆单元的应力
% 输入:单元刚度矩阵k,单元的位移列阵u(2*1),单元横截面积A
% 输出:单元应力stress
stress = k * u/A;1.2 二阶杆单元
二阶杆单元是带中间节点的杆单元,如下图所示,单元节点为i,j,m,杆单元界面为A,弹性模量为E,坐标系为i指向j的x方向。

单元刚度矩阵为:
二阶杆单元有限元分析MATLAB程序主要包括单元刚度矩阵(Bar1D3Node_Stiffness)、单元组装(Bar1D3Node_Assembly)、单元应力(Bar1D3Node_Stress)和节点力(Bar1D3Node_Forces)四个函数,分别如下:
function k = Bar1D3Node_Stiffness(E,A,L)
% 该函数计算二阶杆单元的刚度矩阵
% 输入:弹性模量E,杆的横截面积A和长度L
% 输出:单元刚度矩阵k(3*3)
k = E*A/(3*L)*[7 1 -8;1 7 -8;-8 -8 16];function y = Bar1D3Node_Assemble(K,k,i,j,m)
% 该函数进行二阶杆单元刚度矩阵的组装
% 输入:单元刚度矩阵k和单元节点编号i,j, m
% 输出:整体刚度矩阵K
DOF(1) = i;
DOF(2) = j;
DOF(3) = m;
for n1 = 1:3for n2 = 1:3K(DOF(n1),DOF(n2)) = K(DOF(n1),DOF(n2))+k(n1,n2);end
end
y = K;function forces = Bar1D3Node_Forces(k,u)
% 该函数计算二阶杆单元的节点力
% 输入:单元刚度矩阵k,单元的位移列阵u(3*1)
% 输出:单元节点力forces
forces = k*u;function stress = Bar1D3Node_Stress(k,u,A)
% 该函数计算二阶杆单元的应力
% 输入:单元刚度矩阵k,单元的位移列阵u(3*1),单元横截面积A
% 输出:单元应力stress
stress = k * u/A;2. 二维杆单元有限元分析程序
未完待续....
3. 三维杆单元有限元分析程序
参考文献
曾攀《有限元基础教程》;
相关文章:
[Matlab有限元分析] 2.杆单元有限元分析
1. 一维杆单元有限元分析程序 一维刚单元的局部坐标系(单元坐标系)与全局坐标系相同。 1.1 线性杆单元 如图所示是一个杆单元,由两个节点i和j,局部坐标系的X轴沿着杆的方向,由i节点指向j节点,每个节点有…...
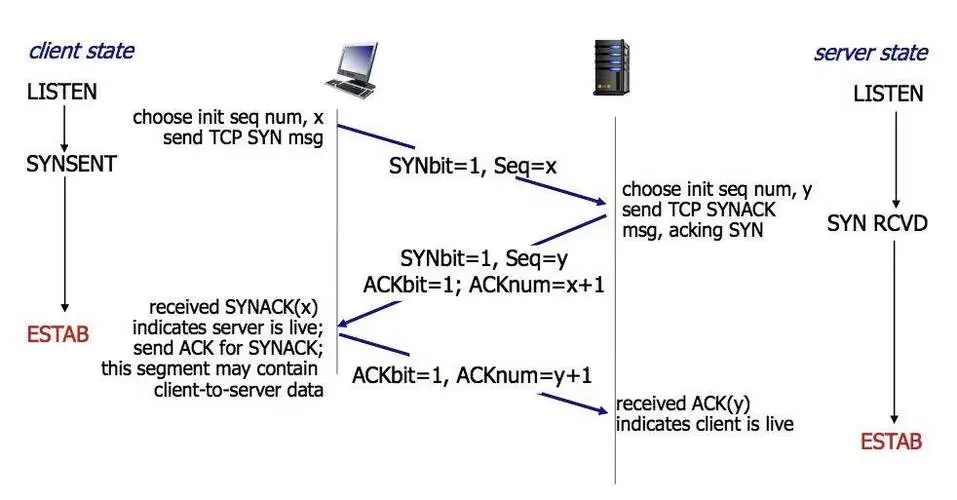
透过对话聊天聊网络tcp三次握手四次挥手
序 说起来网络,就让我想起的就是一张图。我在网上可以为所欲为,反正你又不能顺着网线来打我。接下来我们来详细说一下网络到底是怎么连接的。 TCP三次打招呼 首先我会用男女生之间的聊天方式,来举一个例子。 从tcp三次握手来说,…...
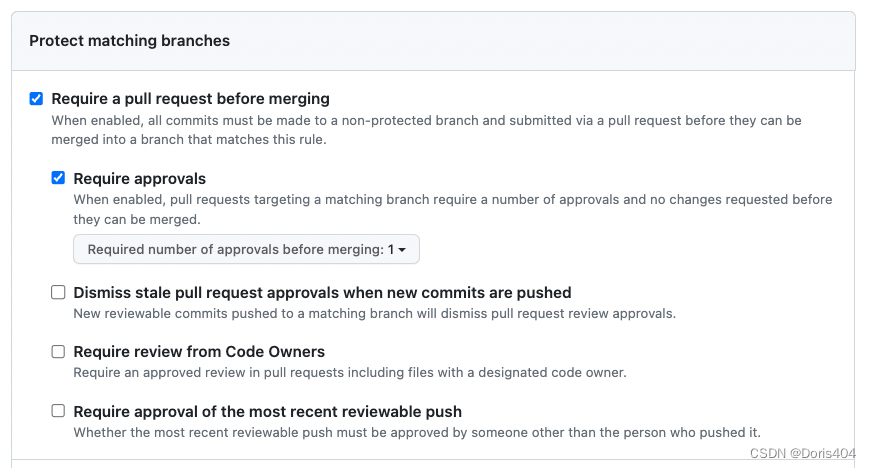
项目管理套路:看这一篇绝对够用❤️
写论文必不可少的,就是创建代码并进行实验。好的项目管理可以让实验进行得更加顺利。本篇博客以一次项目实践为例,介绍项目管理的方法,以及可能遇到的问题,并提供一些可行的解决方案。 目录 项目管理工具开始第一步版本管理十分关…...

华为-算法---测试开发工程师----摘要牛客网
Java面试题---摘要牛客网-CSDN博客package extendNiuKeWang;import java.util.Scanner;public class GoodHuaWei {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int money = sc.nextInt();System.out.println("n值总金额:"+money)…...
python环境搭建-yolo代码跑通-呕心沥血制作(告别报错no module named torch)
安装软件 安装过的可以查看有没有添加环境变量 好的! 我们发车! 如果你想方便快捷的跑通大型项目,那么必须安装以下两个软件: 1.pycharm2.anaconda对应作用: pycharm:专门用来跑通python项目的软件,相当于一个编辑器,可以debug调试,可以接受远程链接调试!anaconda:专…...
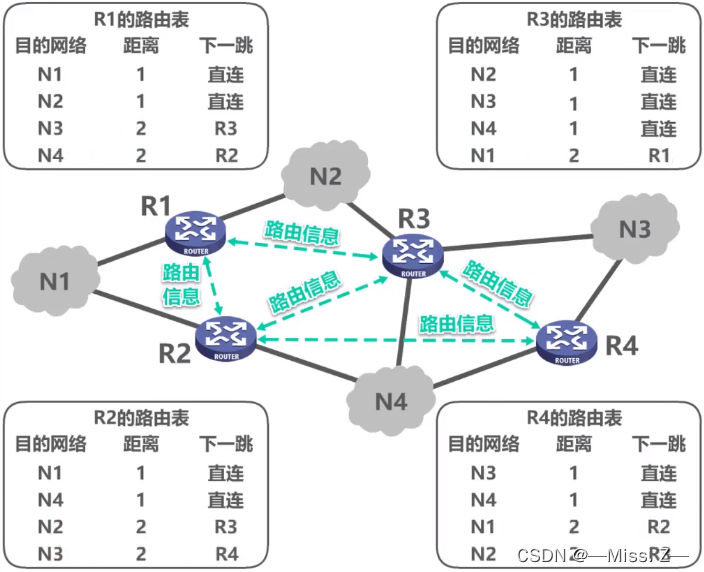
Cisco Packet Tracer配置命令——路由器篇
路由基础 路由器用于互联两个或多个网络,具有两项功能:为要转发的数据包选择最佳路径以及将数据包交换到正确的端口,概括为路由选择和分组转发。 路由选择 路由选择就是路由器根据目的IP地址的网络地址部分,通过路由选择算法确…...
) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins))
setContentsMargins(QMargins()) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins)
setContentsMargins(QMargins()) 是 QWidget 类的成员函数,用于设置小部件的内容边距(Contents Margins)。 在 Qt 中,内容边距指的是小部件内部内容与小部件边界之间的空白区域。通过设置内容边距,可以控制和调整小部…...

Redis key 过期监听实现
1.技术背景,想知道 redis 设置了TTL时间的key 过期,且有后续的业务处理的场景可以使用。 bug点: 使用redis 缓存失效监听会有一定的延迟, 过期事件是在redis服务器删除键的时候生成的,而不是在理论上生存时间到达0值得…...
Gee教程2.上下文Context
先来看看Gin框架的简单例子 func main() {engine : gin.Default()engine.GET("/", func(c *gin.Context) {c.String(http.StatusOK, "hello World!")})//监听并启动服务,默认 http://localhost:8080/engine.Run() }//我们自己写的 func main()…...
【从浅识到熟知Linux】基本指定之cat、more和less
🎈归属专栏:从浅学到熟知Linux 🚗个人主页:Jammingpro 🐟每日一句:写完这篇我要去吃晚饭啦!! 文章前言:本文介绍cat、more和less指令三种查看文件的用法并给出示例和截图…...

2018年7月24日 Go生态洞察:Go Cloud实现便携式云编程
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
storyBook常见踩坑报错 和 解决
用StoryBook官网的代码,但报错,Unexpected token’<’ 在js文件中// Button.stories.js|jsx import { Button } from ‘./Button’; export default { component: Button, }; /* *👇 Render functions are a framework specific featur…...

python 笔记 根据用户轨迹+基站位置,估计基站轨迹+RSRP
1 问题描述 已知用户实际的轨迹,和基站的位置,能不能得到用户所连接的基站,以及基站的信号强度RSRP? 1.1 几个假设 这里我们做几个假设: 每个用户有80%的概率连接最近的基站,有20%的概率选择其他的基站连…...
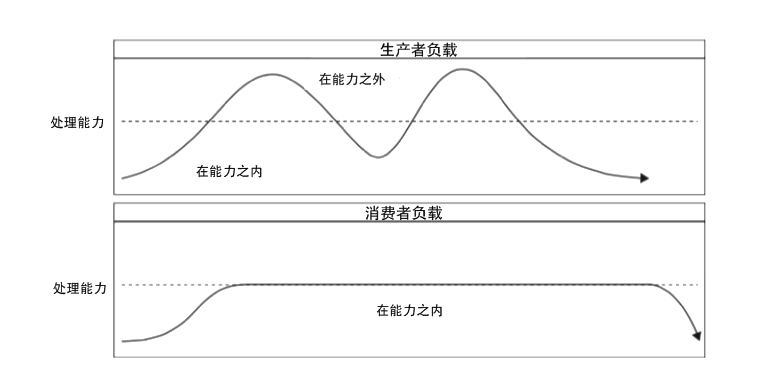
RocketMQ 安装部署及应用场景记录
文章目录 前言一、RocketMQ简介1.1 整体架构 二、RocketMQ安装部署2.1 RocketMQ 下载2.2 修改 JVM 参数2.3 启动 NameServer 和 Broker2.4 验证发送和接受消息2.5 停止 NameServer 和 Broker2.6 配置全局环境 三、RocketMQ应用场景3.1 异步处理3.2 应用解耦3.3 流量削峰 前言 …...

人工智能面面观
人工智能简介 人工智能(Artificial Intelligence,简称AI)是一门研究如何使计算机能够模拟和执行人类智能任务的科学和技术领域。它致力于开发能够感知、理解、学习、推理、决策和与人类进行交互的智能系统。人工智能的背景可以追溯到上世纪50…...

vue-router的使用技巧
一、安装 npm install vue-router 二、引入 main.ts引入 import { createApp } from vue import App from ./App.vue import router from ./routerconst app createApp(App)app.use(router) app.mount(#app)三、定义路由文件 路由的参数 meta添加路由的其他参数 redire…...
CV计算机视觉每日开源代码Paper with code速览-2023.11.21
点击CV计算机视觉,关注更多CV干货 论文已打包,点击进入—>下载界面 点击加入—>CV计算机视觉交流群 1.【基础网络架构:Transformer】Multi-entity Video Transformers for Fine-Grained Video Representation Learning 论文地址&…...

人工智能对当代生活的影响
人工智能(AI)是指通过模拟人类智能的方式,使机器能够执行某些需要智能的任务。随着技术的快速发展和应用的广泛推广,人工智能已经深入到我们的日常生活中,对我们的生活和社会产生了深远的影响。本文将探讨人工智能对当…...
)
笔记:如何搭建一套前端监控系统?(持续更新中)
数据敏感处理 数据加密,对涉及用户隐私的数据做到加密防护 独立部署,不和其它应用共享监控系统 不采集具体数据,只采集用户操作数据 错误采集 Runtime Error: JS运行错误,可通过error监听器捕获 load Error: 资源加载错误&#x…...
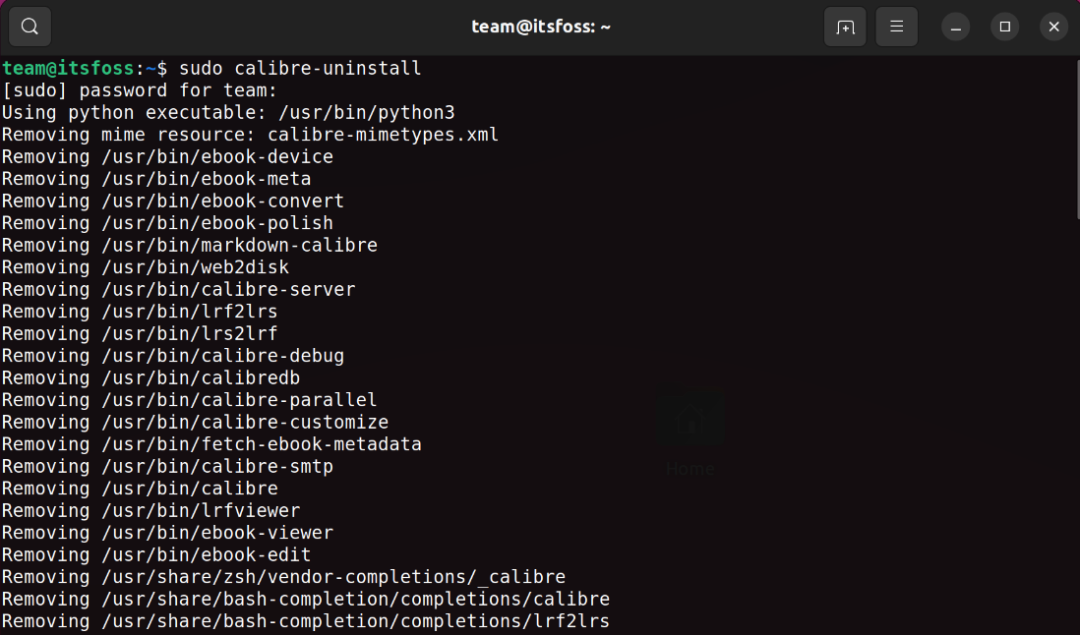
在 Ubuntu 上安装最新版的 Calibre
目录 前言 方法1:从 Ubuntu 的仓库安装 Calibre 卸载 Calibre 方法2:获取最新版本的 Calibre 卸载 Calibre 结语 前言 Calibre 是一款自由开源的电子书软件。下面介绍如何在 Ubuntu Linux 上安装它。 作为电子书管理的瑞士军刀,Calibre …...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
