我的第一次SACC之旅
今年有很多第一次,第一次作为“游客”参加DTCC(中国数据库大会),第一次作为讲师参与ACDU·中国行(成都站),第一次参加OB年度发布会(包含DBA老友会),而这次是第一次参加SACC(中国系统架构师大会)·上海站,而且这次也作为演讲嘉宾在“向量数据库技术探索”专题研讨会中进行了题目为《Oracle AI向量搜索》的主题演讲。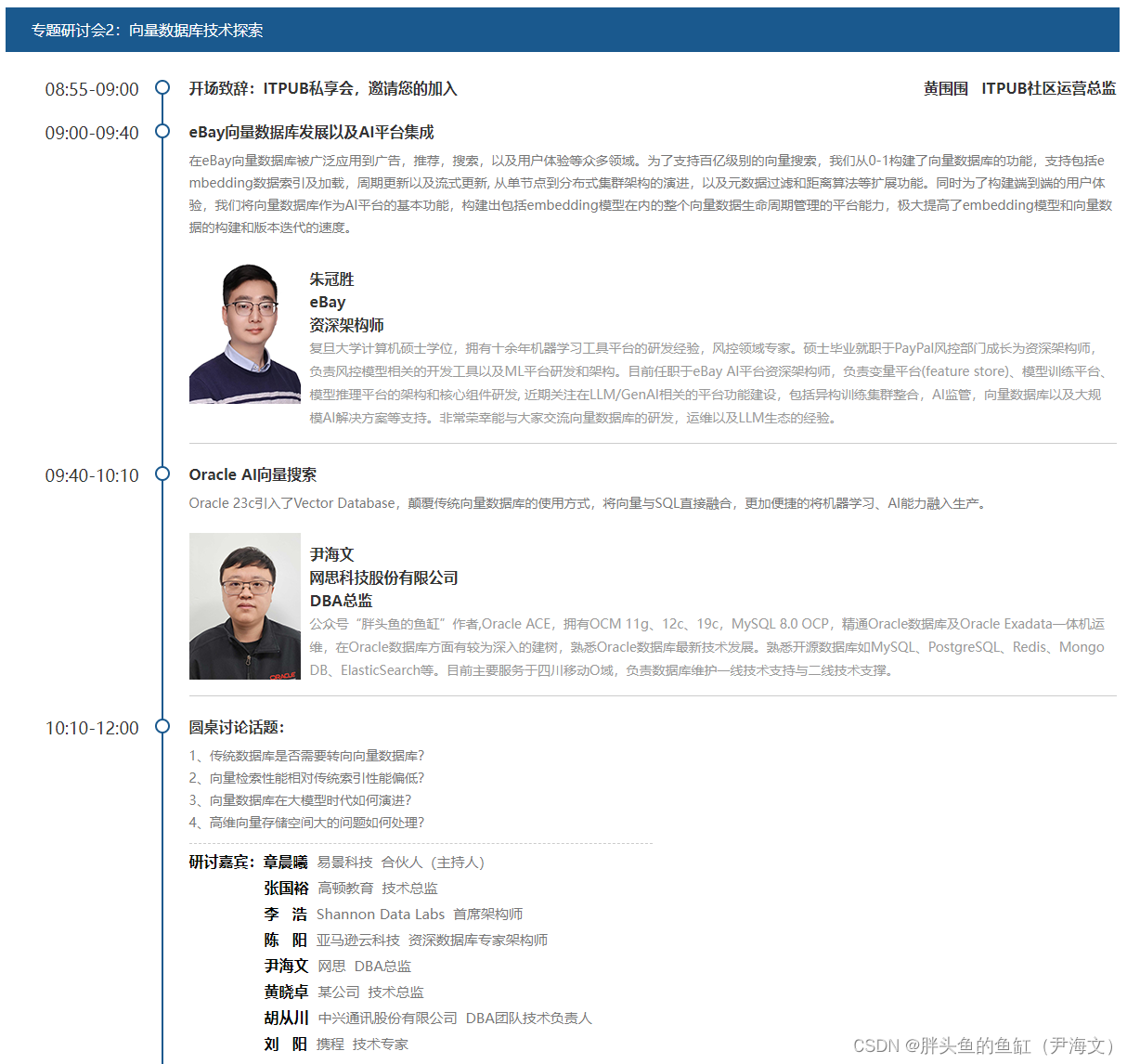
1 向量数据库
作为“向量数据库技术探索”专场的演讲嘉宾,这一堂是我参与最深的两个专场之一。随着ChatGPT的大火,LLM语言大模型的飞速发展,在LLM中出现了幻觉和过时信息的相关问题。通过RAG(检索式增强生成方法),可以让LLM不用重新训练就能够获取最新的信息,基于RAG产生更可靠更专业的输出。实施 RAG 需要向量数据库等技术,这些技术可以快速嵌入(Embedding )新数据,快速搜索数据并输入给LLM。
在这一场我对Oracle在23c正式版中即将发布的Vector数据库中是如何定义向量数据库的存储与使用方式,比如将向量作为一个作为一个新的可配置维度值类型或自适应数据类型引入Oracle数据库中用于存储向量数据,通过一些列新的SQL Embedding函数生成向量数据,一系列新的SQL语法与函数轻松实现表达相似性搜索,并且向量数据可以像传统关系型数据库一样实现DML事务处理,也可以和专用向量数据库一样使用HNSW、IVF等算法对向量进行索引操作。同时作为融合数据库的先驱,向量数据库可以与GIS、文本、JSON、图、关系型数据通过SQL进行融合使用,包含窗口分析函数与存储过程中使用,并且支持JOIN操作。由于目前Oracle 23c还未正式发布,而且相关资料主要源自于Oracle内部,并不能作为最终的产品呈现,所以相关细节我这里就不做分享了。

专场中也有针对专用向量数据库的分享,也做了专用数据库与向量数据库之争的小专题讨论(让我想起了其他的“斗争”),主要在于一下几个点:
- 专用向量数据库确实能在向量这个赛道做到很好的性能与稳定性,而类似于ES插件这种向量支持也能做到快速功能实现。但是由于数据更新操作的缺失,在很多情况下需要,需要预留操作空间给更新操作,且很多产品会出现无用数据(多为过期历史数据)保留的现象,会出现磁盘容量、内存容量方面等问题。(一次全量ChatGPT知识库更新操作的成本是很高的)
- 虽然PG的Vector插件也很火,但是现场多位业内专家也指出了PG在向量方面性能(<60%)与稳定性不佳的问题,对目前情况下通用数据库融合向量提出了质疑。而对于Oracle的向量数据库,虽然从12.1的Inmemory和第一代Exadata开始Oracle就开始使用向量能力来加速通用数据库能力(可以查看数据库管理-第106期 以前版本Oracle数据库中的AI与向量应用(20230921)),向量数据库性能应该会很不错,但是由于没有正式发布与使用,确实没法去判断。
但是大多数向量数据库的使用方也提出了,如果通用数据库能够实现专用数据库80-90%的性能且稳定性没有问题的话,会毫不犹豫转向通用数据库,因为可以不用像专用数据库(主要是不能存放其他类型数据)需要结果的时候在向量数据库查询完成后还需要去其他数据库做匹配的几步走操作;同时完整的事务支持也能很好的对向量数据进行删改,可以极大节省磁盘与内存空间。
薛首席有句总结很好“平时随意拍照肯定用手机,但是婚纱照可能就会找专业照相”,总结下来还是与使用场景和程度有关,因此未来向量数据库何去何从,还得看各家发展情况。
2 成本到底该咋算
参加比较深入的第二场则是主要是给薛首席捧场的“FinOps实践:云成本管理与优化”专题研讨会,同时也被会务组“强制”加入了本场嘉宾行列。(我和薛老师俩搞数据库的,来云相关专场“砸场子”,属实是…干得漂亮)

众所周知,我主要给移动做服务,没有上云机会,而薛首席作为国企…呸!央企,也是没有上云机会的,反而我俩可以更加的…不中立吧。其实FinOps我也是知道点皮毛,听会中来自大佬分享有了进一步的了解,但我有一些疑问吧:
- 不是所有地方都能上云,而FinOps主要还是针对公有云上的成本估算与降本增效(当然B站老师也提到了也想用于自建私有云)
- FinOps目前还主要用于云上的基础设施方面,但是对于研发层面(我认为是包含架构选型、研发质量这些)向上的几乎没有,而且对基础设施本身人力投入这块也是缺失的,我认为需要补齐。
还是最后还是用薛首席的一句话来结束这一节“砍掉不需要的需求比其他方式效果更好吧”。

(注:图文内容无直接关系)
3 扩展与展望
直接上大佬合影图,这次又认识了很多数据库or非数据库方面的大佬,收货良多啊:

今年完成了各种参会的第一次,明年应该还会参加很多,一方面是拓宽自己的眼界,见识更多,结识更多;另一方面也是给公司做做宣传,也希望能从这些会中汲取一些东西能给公司发展提供一些助力。
预告一下,明年DTCC已经报名作为演讲嘉宾,预约了一个专场,就希望到时候薛首席不要仅仅当个主持人。
相关文章:

我的第一次SACC之旅
今年有很多第一次,第一次作为“游客”参加DTCC(中国数据库大会),第一次作为讲师参与ACDU中国行(成都站),第一次参加OB年度发布会(包含DBA老友会),而这次是第一…...
)
Codeforces Round 908 (Div. 2)
Codeforces Round 908 (Div. 2) 文章目录 Codeforces Round 908 (Div. 2)ABCD A 获取对战的最后一个即为胜者 #include <bits/stdc.h>using namespace std;void solve() {int n;cin >> n;string s;cin >> s;cout << s[n-1] << endl; }int main…...
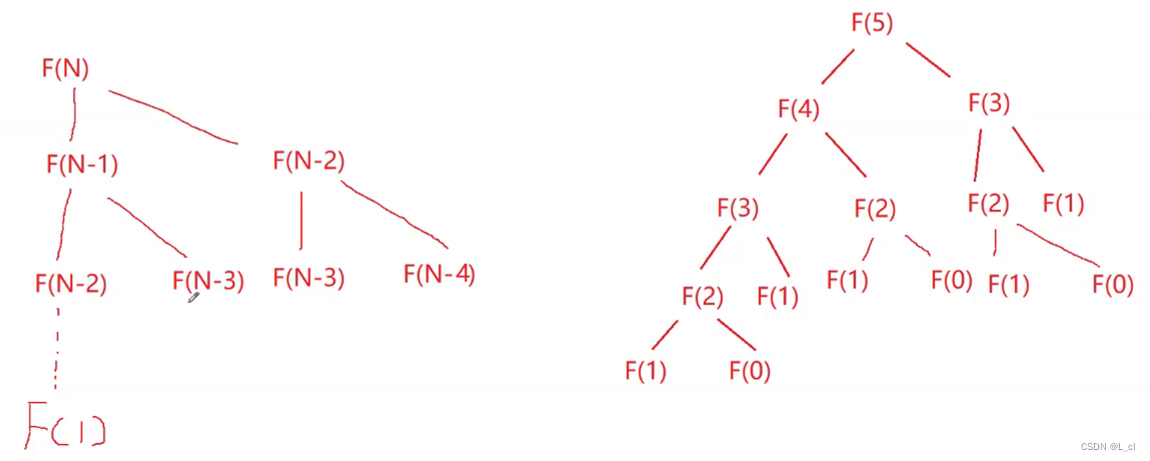
Java实现-数据结构 2.时间和空间复杂度
.如何衡量一个算法的好坏:时间复杂度和空间复杂度 算法效率分为时间效率和空间效率,时间效率称为时间复杂度,空间效率称为空间复杂度 时间复杂度 算法的时间复杂度是一个数学函数,它描述了算法的运行时间,一个算法执…...

Docker exec命令
docker exec :在运行的容器中执行命令。 语法: docker exec [OPTIONS] CONTAINER COMMAND [ARG...]OPTIONS说明: -d:分离模式: 在后台运行 -i:即使没有附加也保持STDIN打开 -t:分配一个伪终…...

可燃气体监测仪助力燃气管网安全监测,效果一览
城市地下管线是指城市范围内供应水、排放水、燃气等各类管线及其附属设施,它们是保障城市正常运转的重要基础设施且影响着城市生命线。其中燃气引发的事故近些年不断增加,由于燃气管线深埋地下环境复杂,所以仅仅依赖人工巡查难以全面有效地防…...
在WSL搭建Schema Registry)
Kafka(二)在WSL搭建Schema Registry
目录 1 Avro与Schema Registry2 搭建Schema Registry2.1 下载Confluent并解压2.2 设置环境变量2.3 修改配置2.4 启动服务 3 API列表 1 Avro与Schema Registry Apache Avro 是一种高效的数据序列化系统,用于在不同的应用程序和平台之间传输和存储数据。它提供了一种…...
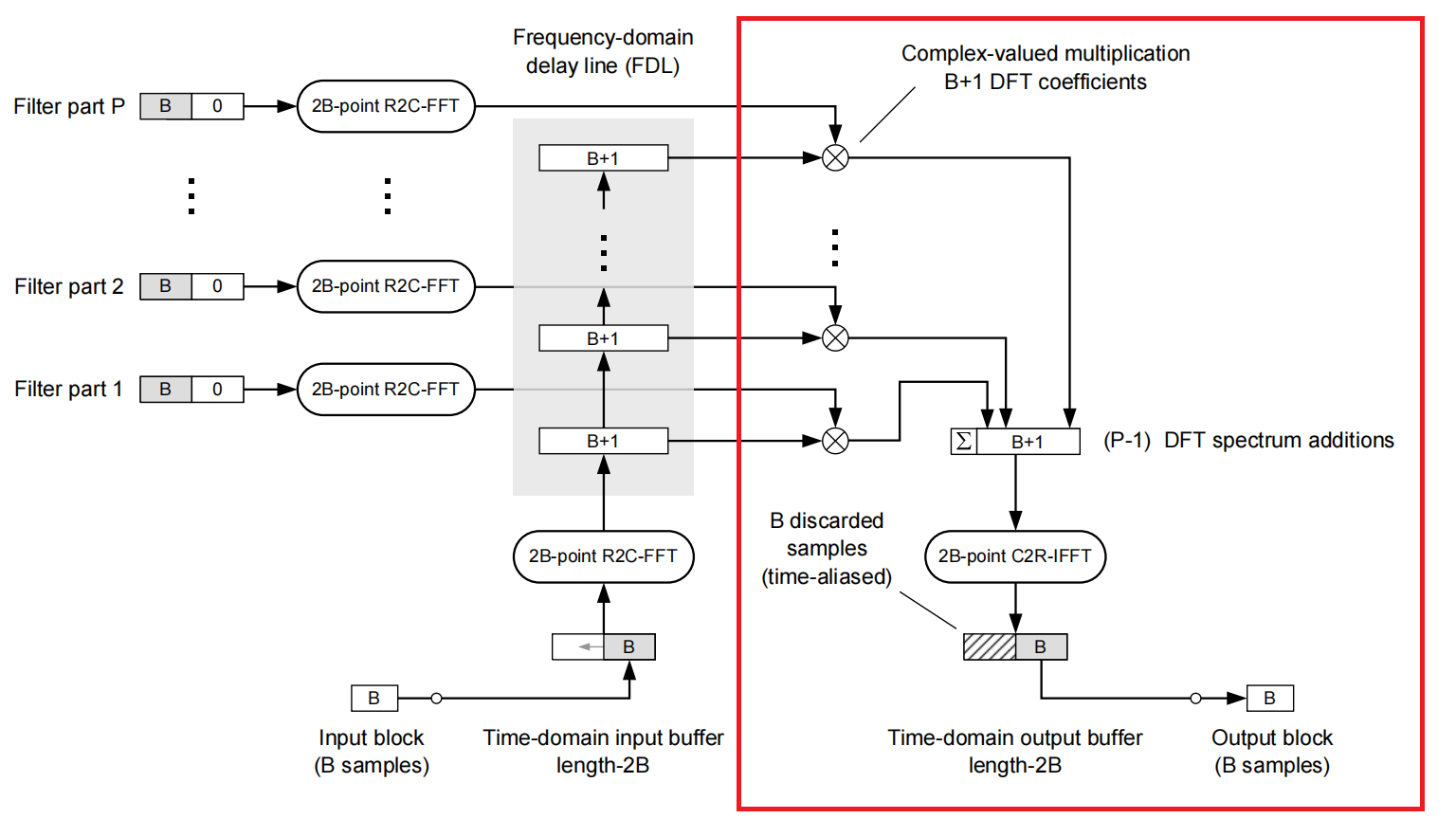
webrtc AEC 线性滤波 PBFDAF(均匀分块频域自适应滤波)介绍
计算一个脉冲响应和输入信号的卷积,除了使用原始的时域卷积以外,还有如下方法: FFT卷积的方法:对输入信号(长度M)和脉冲响应(长度N)分别补零到K(K>MN-1),…...

开源vs闭源,处在大模型洪流中,向何处去?
文章目录 一、开源和闭源的优劣势比较1.1 开源优势1.2 闭源的优势 二、开源和闭源对大模型技术发展的影响2.1 数据共享2.2 算法创新2.3 业务拓展2.4 安全性和隐私2.5 社会责任和伦理 三、开源与闭源的商业模式比较3.1 盈利模式3.2 市场竞争3.3 用户生态3.4 创新速度 四…...

web前端之vue和echarts的堆叠柱状图顶部显示总数、鼠标悬浮工具提示、设置图例的显示与隐藏、label、legend、tooltip
MENU 效果图htmlJavaScripstyle解析 效果图 html <template><div><div><div id"idStackedColumnChart" style"width: 100%; height: 680px"></div></div></div> </template>JavaScrip export default {…...
Excel表中合并两个Sheet的方法?
按AltF11,调出Visual Basic 界面。 在左侧窗口中,右键选择“插入”—“模块”: 将如下代码粘贴进去,点击运行按钮,完成数据表合并。 Sub MergeAllSheetsInThisWorkbook() On Error Resume Next Application.ScreenU…...

1个10进制数转为2进制和转为8进制, 各位上数字后2进制的值与8进制的值相同的值有 1 8 9 64 问第23个值是多少?
1个10进制数转为2进制和转为8进制, 各位上数字后2进制的值与8进制的值相同的值有 1 8 9 64 问第23个值是多少? #define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <malloc.h> #include<cmath&g…...

27、Nuxt.js项目整合ElementUI组件库
参考element-ui官网安装组件库 项目中新建插件引入element-ui plugins\element-ui.js import Vue from vue; import ElementUI from element-ui;Vue.use(ElementUI);nuxt.config.js plugins: ["/plugins/element-ui.js"],build: {// 将位于 node_modules 目录下的…...

设计问卷调查问题的9大技巧!技巧1:明确目标与问题
我们在设计问卷调查时要考虑很多因素,其中问卷问题是需要关注的重要因素之一。有效的问题能够帮助我们获取到有用的信息,让问卷结论更准确。怎么设计问卷调查的问题呢?本文就为大家提供几个设计问题时的神仙技巧! Tip1࿱…...
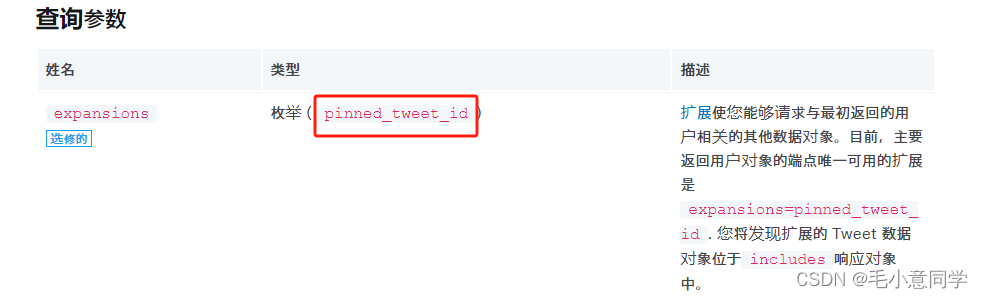
java代码调用twitter-api用例实战
一、申请twitter开发者账号 首先先申请twitter开发者免费的API,要填写申请的内容,放心大胆地写,申请完,会提供免费的API接口。 以下是我申请到的三个免费API 申请完开始进行测试调用。 读官方文档账户认证那块:https…...
】)
UniWebView的更新日志【### 5.3.0 (28 Jan, 2023)】
UniWebView的更新日志 # Release Note ### 5.3.0 (28 Jan, 2023) #### Add * Support for customization of Kotlin and Android Browser package versions. This can help to resolve the conflict with other plugins which use another version of these packages. ###…...
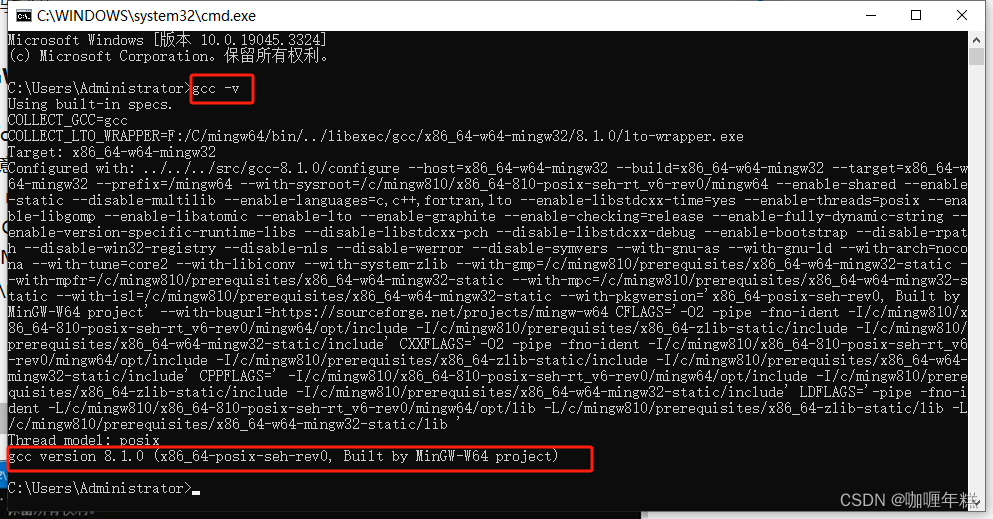
【VScode】安装配置、插件及远程SSH连接
一、VSCode安装 二、配置安装插件 三、配置远程连接SSH 四、MinGW 一、VSCode安装 VS官网 Visual Studio Code - Code Editing. Redefined下载安装包: 二、配置安装插件 安装中文插件 配置字体为20 配置文件–>首选项->设置->Font Size为20 设置 VSC…...

IOS Frida 常用脚本
调用堆栈 console.log("bt:" + Thread.backtrace(this.context,Backtracer.ACCURATE).map(DebugSymbol.fromAddress).join(\n\t)); Hook 调用,修改返回值 // Get a reference to the openURL selectorvar openURL = ObjC.classes.UIApplication["- openURL:&qu…...

vuex actions异步请求 跟module模块化
actions vuex里面的异步操作,接受参数context ,参数有commt,getters,state 列如:调用 mutations 方法实现修改state 数据 (只能通过mutations 修改 state 数据) state:()>{count: 0, }mutations: {addCount(state)…...

医学图像分割:U_Net 论文阅读
“U-Net: Convolutional Networks for Biomedical Image Segmentation” 是一篇由Olaf Ronneberger, Philipp Fischer, 和 Thomas Brox发表的论文,于2015年在MICCAI的医学图像计算和计算机辅助干预会议上提出。这篇论文介绍了一种新型的卷积神经网络架构——U-Net&a…...

从0到0.01入门 Webpack| 008.精选 Webpack面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
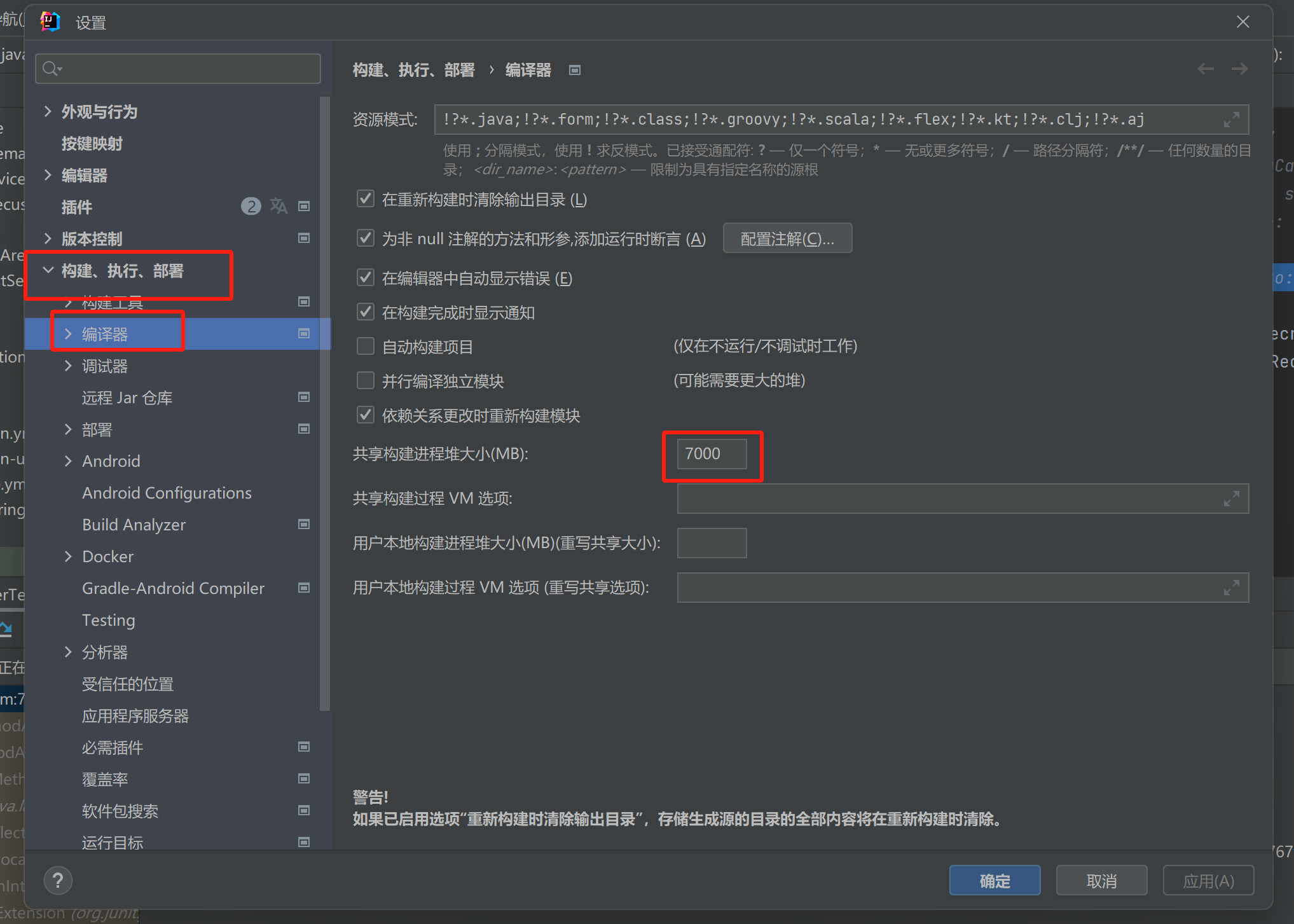
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
