【数据结构】堆的详解
本章的知识需要有树等相关的概念,如果你还不了解请先看这篇文章:初识二叉树
堆的详解
- 一、二叉树的顺序结构及实现
- 1、二叉树的顺序结构
- 2、堆的概念及结构
- 二、堆的简单实现 (以大堆为例)
- 1、堆的定义
- 2、堆的初始化
- 3、堆的销毁
- 4、堆的打印
- 5、堆的插入
- 6、堆顶元素的获取
- 7、堆的删除
- 8、堆元素个数的获取
- 8、堆的判空
- 10、堆简单的应用
- 三、堆的创建
- 1、向上调整建堆
- 2、向下调整建堆
- 四、堆的应用
- 1、堆排序
- 2、TOP-K问题
一、二叉树的顺序结构及实现
1、二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
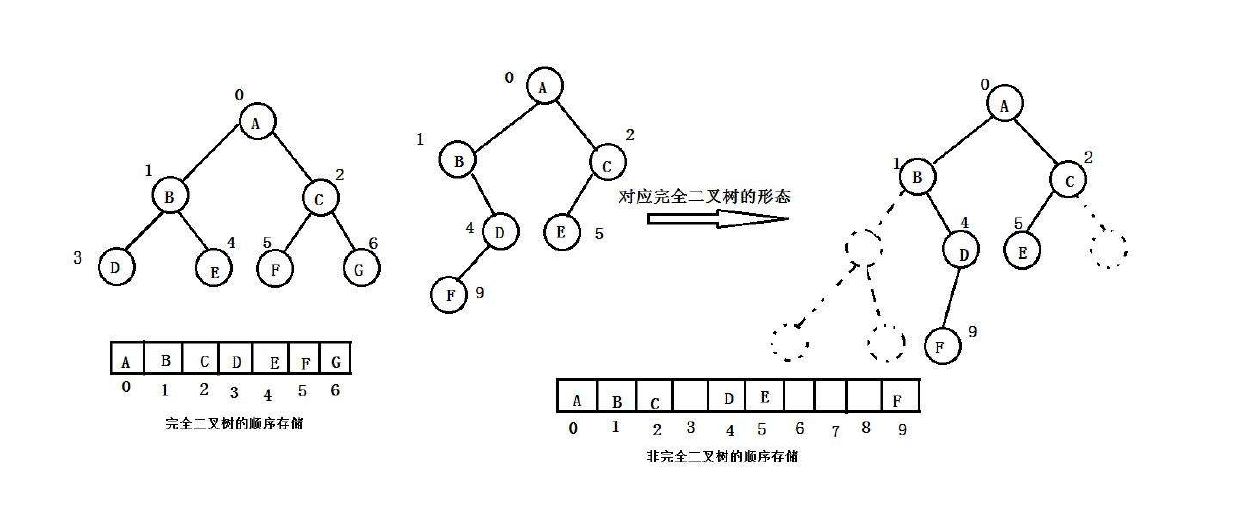
2、堆的概念及结构
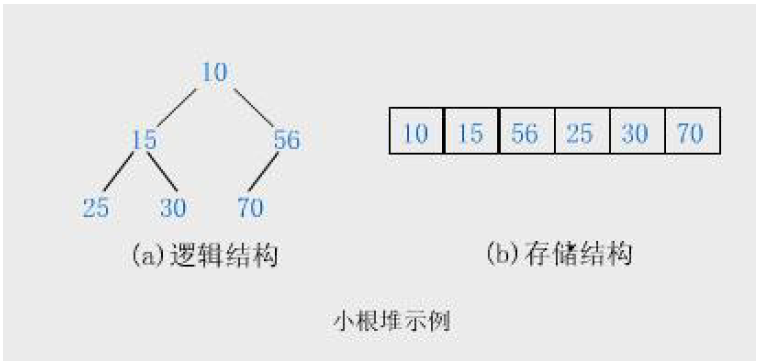
严格定义:如果有一个关键码的集合K=K=K={ k0,k1,k2,..,kn−1k_0,k_1, k_2,..,k_{n-1}k0,k1,k2,..,kn−1 },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足: Ki<=K2i+1K_i<= K_{2i+1}Ki<=K2i+1且Ki;<=K2∗i+2(Ki>=K2i+1且Ki>=K2∗i+2)i=0,1,⋅⒉...,K_i;<= K_{2*i+2}(K_i>= K_{2i+1}且K_i>= K_{2*i+2}) i=0,1,·⒉...,Ki;<=K2∗i+2(Ki>=K2i+1且Ki>=K2∗i+2)i=0,1,⋅⒉...,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
非严格定义:堆有两种,分为大堆与小堆,它们都是完全二叉树!
大堆:树中所有父亲都大于等于孩子
小堆:树中所有父亲都小于等于孩子

在前一篇文章中我们也讲过,左孩子都是奇数,右孩子都是偶数,并且孩子和父亲下标也是有一定关系的(我们也可以通过找规律得到下面的关系):
leftchild = parent*2+1
rightchild = parent*2+2
parent = (child-1)/2 //偶数会被取整数,因此可以直接按照左孩子公式反推
二、堆的简单实现 (以大堆为例)
1、堆的定义
由于堆比较适合用数组存储,我们可以按照顺序表的结构来进行定义,但是切记数组存储是物理结构,我们要把这个物理结构给抽象为完全二叉树。
//堆的结构定义
typedef int HPDateType;
typedef struct Heap
{HPDateType* a; //指向要存储的数据int size; //记录当前结构存储了多少数据int capacity; //记录当前结构的最大容量是多少
}HP;
2、堆的初始化
堆的初始化,我们可以给指针a开辟空间,也可以不开辟空间,这里选择不开辟空间。
//堆的初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}
3、堆的销毁
堆的销毁我们可以直接将空间进行释放,然后将指针置空size与capacity置成0就行了。
//堆的销毁
void HeapDestroy(HP*php)
{assert(php);free(php->a); //指针置空php->a = 0; //size置成0php->size = php->capacity = 0; //capacity置成0
}
4、堆的打印
由于我们是使用数组实现堆,我们可以直接遍历一遍数组将它们打印出来就行了。
//堆的打印
void HeapPrint(HP* php)
{assert(php);int i = 0;for (i = 0; i < php->size; ++i){printf("%d ", php->a[i]);}
}
5、堆的插入
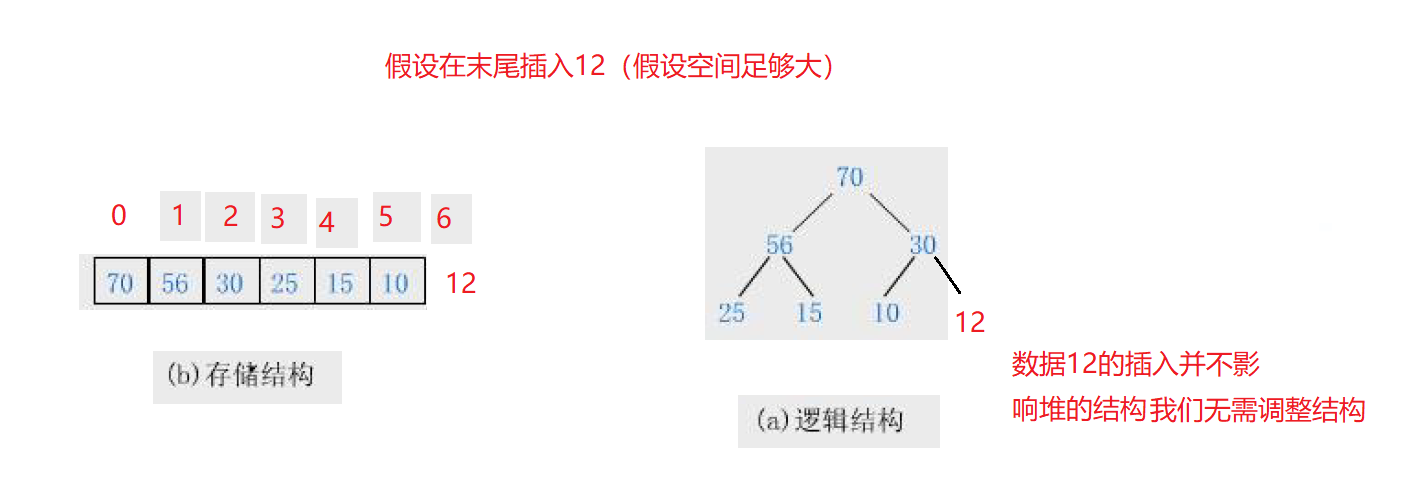
堆的插入就有一些复杂了,我们的插入数据以后要保证插入数据后的堆,还是一个大堆,不然就破坏了堆的结构。
我们先来考虑第一种情况:
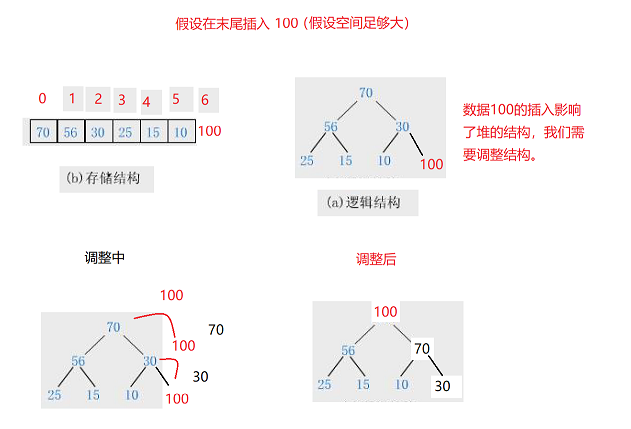
我们再来考虑第二种情况:
我们总结一下这两种情况:
①首先在我们插入数据(子节点)之前,原始堆就要满足堆的结构,否则就是前面的代码出现了问题,与我们插入的数据无关!
②然后插入的子节点要与其父节点进行比较,如果小于其父节点则不交换,正常插入。如果其插入的子节点大于父节点就要进行向上调整交换,这个交换次数是不确定的,可能是一次也可能是两次,不过最多就是树的高度h=log2Nh=\log_2Nh=log2N次(NNN为节点个数),这也就是说我们的堆的插入是时间复杂度是O(log2n)O(\log_2n)O(log2n)
接下来就是我们要根据这两种情况写出相应的代码了,这个时候这个孩子和父亲下标关系就很重要了,通过这个关系我们就能由子节点找到父节点,由父节点找到子节点了。
//堆的插入
void HeapPush(HP* php, HPDateType data)
{assert(php);//判断是否需要扩容if (php->capacity == php->size){int new_capacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDateType* tmp = (HPDateType*)realloc(php->a, sizeof(HPDateType)*new_capacity);//realloc对于没有进行动态内存分配过的指针 调用会相当与一次mallocif (NULL == tmp){perror("malloc fail:");exit(-1);}php->a = tmp;php->capacity = new_capacity;}//数据插入php->a[php->size] = data;php->size++;//向上调整AdjustUp(php->a,php->size-1);
}
其中向上调整算法非常重要!!!
//交换函数
void Swap(HPDateType* x, HPDateType* y)
{HPDateType tmp = *x;*x = *y;*y = tmp;
}
//向上调整
void AdjustUp(HPDateType*a,int child)
{assert(a);int parent = (child - 1) / 2; //找到刚插入的节点的父节点while (child>0) //child=0说明子节点已经调整到了堆顶,已经不需要再进行调整了。{if (a[child] > a[parent]) //子节点比父节点大就交换{Swap(&a[child], &a[parent]);child = parent; //更改孩子的下标,方便继续与上面新的父节点比较parent = (child - 1) / 2; //更改父节点的下标,方便继续与下面新的子节点比较}else{break;//比较不满足条件,说明数据经过调整后已经符合大堆了}}
}
6、堆顶元素的获取
对于堆来说,堆顶的数据一定是堆里面最大或最小的数,所以堆顶数据的获取还是很有必要的,它的实现也并不复杂。
//堆顶元素的获取
HPDateType HeapTop(HP*php)
{assert(php);assert(php->size > 0);return php->a[0];
}
7、堆的删除
对于堆的删除,一般是删除堆顶元素,因为除了堆顶元素其他元素删除的意义并不大,但是堆顶的元素删除又会破环堆的结构。

而且如果采用直接删除堆顶元素,其他元素向前挪动之后再进行调整的话,会有很大的浪费,因为数组向前挪动的时间复杂度是O(n)O(n)O(n)。但是数组的尾删效率很高是O(1)O(1)O(1),所以数组尽量进行尾删。
于是便有了一种良好的先交换再向下调整的算法,它的思想是:先让堆顶元素与最后一个元素交换位置,这样原先的堆顶元素就变成了堆底元素,然后删除堆底元素,再对堆顶的元素进行向下调整,其核心算法就在于向下调整。
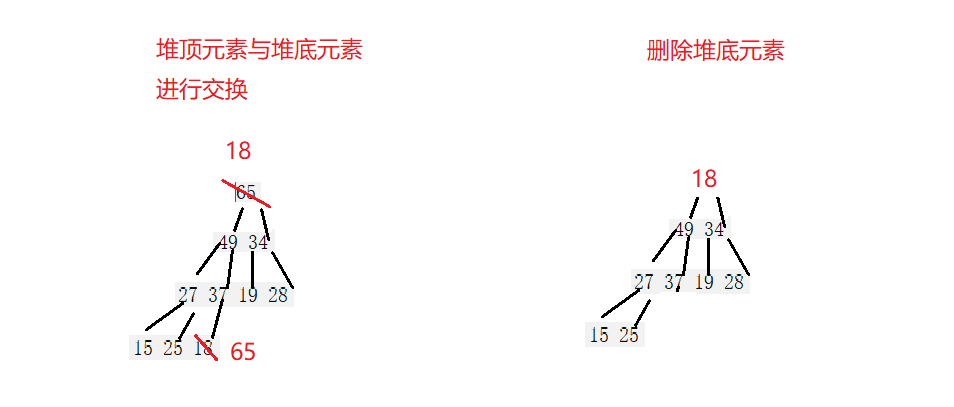
向下调整算法
向下调整算法要求我们:先取堆顶元素的子节点中较大的那个与堆顶元素进行比较,如果子节点大于父节点就进行交换,然后父节点的下标变到原先子节点的下标,再次执行上面的步骤,取父节点下面较大的子节点进行比较换位…
直到子节点不大于父节点或者是超出了数组边界。
//堆的删除
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);//交换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//向下调整AdjustDown(php->a,php->size,0);
}
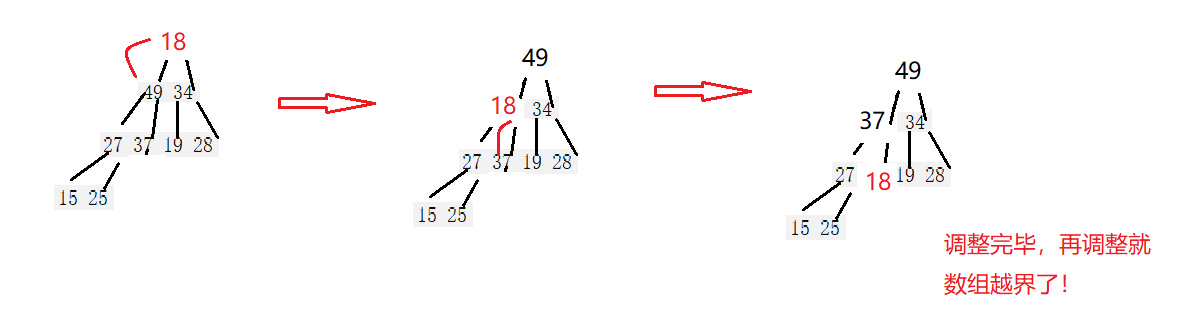
向下调整算法:
//向下调整
void AdjustDown(HPDateType* a, int n, int parent)
{//假设左孩子是最大的int child = parent * 2 + 1;while (child<n){//判断假设是否正确,若不正确进行更改if (a[child + 1] > a[child]){++child;}if (child + 1 < n && a[child] > a[parent]){Swap(&a[child],&a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
向下调整的算法与向上调整类似,这个交换次数是不确定的,可能是一次也可能是两次,不过最多就是树的高度h=log2Nh=\log_2Nh=log2N次(NNN为节点个数),这也就是说我们的堆的删除是时间复杂度也是O(log2n)O(\log_2n)O(log2n)
比较一下向上调整算法与向下调整算法
- 向上调整算法要求,数据插入之前原先的数据已经是一个堆了,才能重新建堆。
- 向下调整算法的要求:左右子树必须是一个堆,才能调整重新建堆。
8、堆元素个数的获取
堆中的元素个数其实就是堆数据结构中的size。
// 堆元素个数的获取
int HeapSize(HP* php)
{assert(php);return php->size;
}
8、堆的判空
//堆的判空
bool HeapEmpty(HP* php)
{assert(php);return (php->size == 0);
}
10、堆简单的应用
学习到了这里,我们其实已经能利用堆处理一些问题了。
- TOP-K问题
堆顶的元素是最大(小)的元素,我们可以取堆顶K次删除K次,拿到一个数据集中最大(小)的前K个。
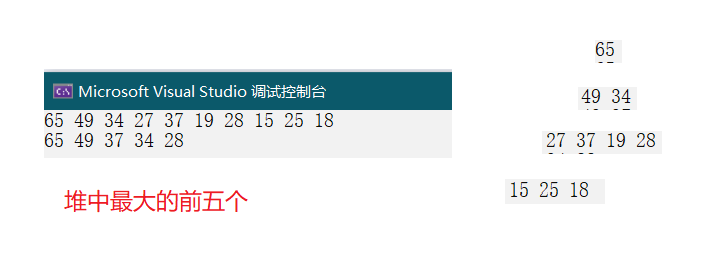
int main()
{HP hp;HeapInit(&hp); //堆的初始化int arr[] = { 27,15,19,18,28,34,65,49,25,37 };for (int i = 0; i < sizeof(arr) / sizeof(int); ++i) //堆的插入,建堆{HeapPush(&hp, arr[i]);}HeapPrint(&hp); //打印堆中的元素printf("\n");//选出最大的前五个int k = 5;for (int i = 0; i < k; i++){printf("%d ", HeapTop(&hp)); //取堆顶的元素HeapPop(&hp); //删除堆顶元素,重新定位新的最大的。}HeapDestroy(&hp); //堆的销毁,防止内存泄漏return 0;
}
- 排序问题
排序问题与TOP-K问题类似,只不过这里的K是所有元素。
int main()
{HP hp;HeapInit(&hp);int arr[] = { 27,15,19,18,28,34,65,49,25,37 };for (int i = 0; i < sizeof(arr) / sizeof(int); ++i){HeapPush(&hp, arr[i]);}HeapPrint(&hp);printf("\n");//排序while(!HeapEmpty(&hp))//只要不为空就一直进行排序。{printf("%d ", HeapTop(&hp));HeapPop(&hp);}HeapDestroy(&hp);return 0;
}
三、堆的创建
在上面的代码中我们看到我们经常会用一个数组去创建堆,因此我们还是很有必要再写一个函数——堆的创建!在上面的代码中我们创建一个堆其实是用的是堆的插入,即将数据插入到数组最后,再进行向上调整。这种方法能帮我们完成堆的创建,但是它的效率并不是很高,我们可以对其做一定优化。
1、向上调整建堆
- 利用堆的插入进行堆的创建
void HeapCreat(HP* php, HPDateType* arr, int n)
{assert(php);HPDateType* tmp = (HPDateType*)malloc(sizeof(HPDateType) * n);if (NULL == tmp){perror("malloc fail:");exit(-1);}php->a = tmp;php->capacity = n;for (int i = 0; i < n; ++i){HeapPush(php, arr[i]);//这里使用了AdjustUp()函数}
}
但是这种建堆算法效率比较低,我们来求一下它的时间复杂度。
按照最坏的情况来算(完全二叉树的最坏情况是满二叉树,且每个节点都要调整):
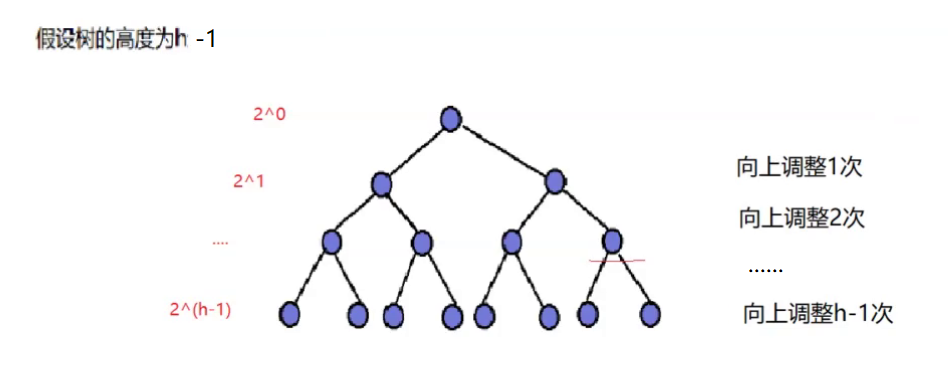
向上调整建堆的第一层是不进行调整的,设FFF是建堆交换调整的总次数,h−1h-1h−1是树的高度,NNN是树的结点个数,则有
F=21∗1+22∗2+23∗3+......+2h−2∗h−2+2h−1∗h−1F=2^1*1+2^2*2+2^3*3+......+2^{h-2}*h-2+2^{h-1}*h-1 F=21∗1+22∗2+23∗3+......+2h−2∗h−2+2h−1∗h−1
利用错位相减法得:
F=(h−2)∗2h+1(1)F=(h-2)*2^h+1 \tag{1} F=(h−2)∗2h+1(1)
又因为二叉树满足:
N=20+21+22+23+......+2h−2+2h−1=2h−1(2)N=2^0+2^1+2^2+2^3+......+2^{h-2}+2^{h-1}=2^h-1\tag{2} N=20+21+22+23+......+2h−2+2h−1=2h−1(2)
将(2)带入(1)中得:
F=(N+1)∗(log2(N+1)−2)+1(3)F=(N+1)*(\log_2{(N+1)}-2)+1\tag{3} F=(N+1)∗(log2(N+1)−2)+1(3)
因此向上调整建堆的时间复杂度是O(nlog2n)O(n\log_2n)O(nlog2n)
2、向下调整建堆
向下调整算法是有的要求的:左右子树必须是一个堆,才能调整重新建堆,但给我们的数组本身就是乱序的,那我们应该怎样才能保证左右子树是一个堆呢?
答案是:我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
在这里第一个非叶子节点的子树是28,我们可以通过子节点与父节点的关系找到28的下标,然后向下调整,让①区域变成堆,然后下标减一到18的位置,然后向下调整,让②区域变成堆,然后下标减一到19的位置,然后向下调整,让③区域变成堆…直到下标为零时再调整一次这样就把堆给建立起来了。
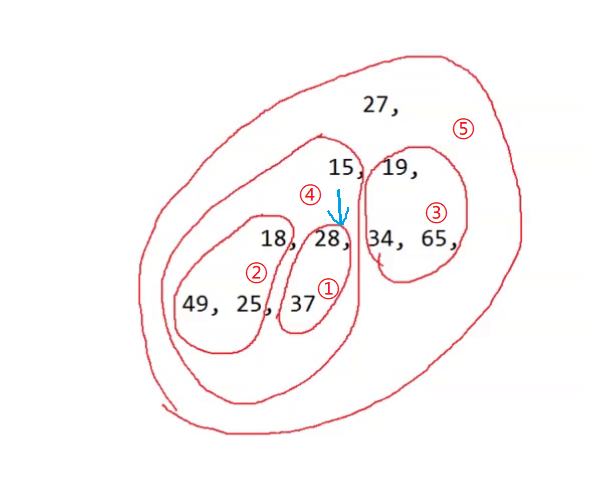
代码实现:
//堆的创建
void HeapCreat(HP* php, HPDateType* arr, int n)
{assert(php);HPDateType* tmp = (HPDateType*)malloc(sizeof(HPDateType) * n);if (NULL == tmp){perror("malloc fail:");exit(-1);}php->a = tmp;php->size=php->capacity = n;memcpy(php->a, arr, sizeof(HPDateType)*n);//内存拷贝函数for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i); //利用向下调整算法}}
这种建堆算法效率是比较高的,我们来求一下它的时间复杂度。
按照最坏的情况来算(完全二叉树的最坏情况是满二叉树,且每个节点都要调整):
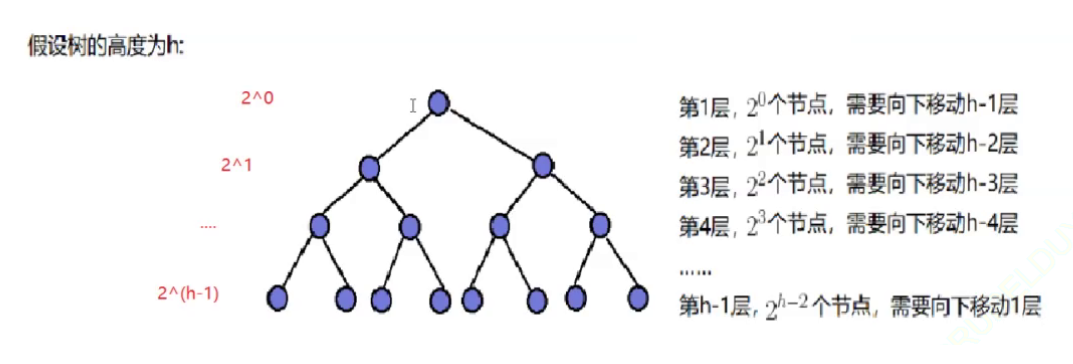
由于向下调整建堆是从倒数第二层开始调整的,所以我们假设树的高度为hhh,FFF是建堆交换调整的总次数,NNN是树的结点个数。
F=2h−2∗1+2h−3∗2+2h−4∗3+......+21∗h−2+20∗h−1(1)F=2^{h-2}*1+2^{h-3}*2+2^{h-4}*3+......+2^1*h-2+2^0*h-1\tag{1} F=2h−2∗1+2h−3∗2+2h−4∗3+......+21∗h−2+20∗h−1(1)
利用错位相减法得:
F=2h−(h+1)(2)F=2^h-(h+1) \tag{2} F=2h−(h+1)(2)
又因为二叉树满足:
N=20+21+22+23+......+2h−2+2h−1=2h−1(2)N=2^0+2^1+2^2+2^3+......+2^{h-2}+2^{h-1}=2^{h}-1\tag{2} N=20+21+22+23+......+2h−2+2h−1=2h−1(2)
将(2)带入(1)中得:
F=N−(log2(N+1)+1)(3)F=N-(\log_2{(N+1)}+1)\tag{3} F=N−(log2(N+1)+1)(3)
因此向下调整建堆的时间复杂度是O(n)O(n)O(n)
综上所述:向下调整建堆是更好的算法。
对比我们也可以发现,向上调整算法是那一层节点越多,向上调整越多,而向下调整算法是那一层节点越少,向下调整越多。因此向下调整算法更加优秀!
四、堆的应用
在前面我们已经简单说过了堆的应用:TOP-K与排序。
1、堆排序
但是上面的应用我们都是借助了堆这个数据结构(利用了堆的插入与删除)在实际应用时,给你一个数组让你进行排序,难道我们还要费很大的力气去建堆?这样显然太慢了,所以我们需要找到一种不用建立堆的数据结构就能进行排序的算法。
首先经过前面的学习我们都知道了,每个连续存储的数组可以看成一个完全二叉树,因此我们可以利用刚才堆的创建的思路对数组里面的数据进行建堆,然后进行排序。
但是假设我们要建立升序数组,我们应该建立大堆还是小堆呢?
- 我们先来看看小堆怎么样。
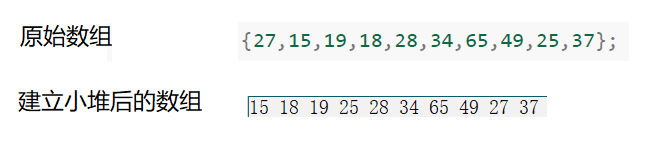
假设我们建立小堆的话,第一个元素就不用进行排序了,我们从第二个进行排序,但是从第二个元素开始重新排序的话我们的堆结构可能就被破坏了,不利于我们后续选数据,要不就是遍历一遍选一个数,这些效率都不太好。因此小堆并不适合建立升序数组。
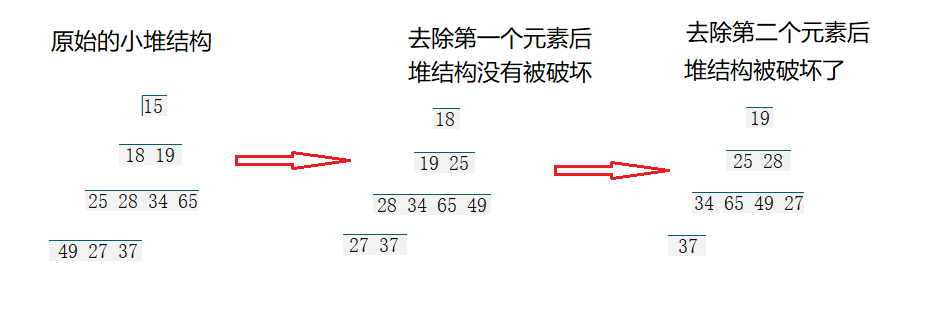
- 我们再来看看大堆
我们可以将堆顶元素与堆底元素进行换位,这样我们最大的元素就到了正确的位置,然后对堆顶元素向下调整一次便可以重新建堆(因为左子树与右子树关系没有改变),再然后把最后一个元素不看成堆里面的元素,再将堆顶元素与堆底元素进行换位,这样我们次大的元素就到了正确的位置,然后对堆顶元素向下调整一次便可以重新建堆,再然后把最后两个元素不看成堆里面的元素如此继续循环往复,等数组里面的数被遍历一遍后,排序也就结束了,另外我们向下调整一次最多交换高度次(log2n)(\log_2n)(log2n),因此堆排序的时间复杂度是O(nlog2n)O(n\log_2n)O(nlog2n)。

//堆排序 升序建立大堆,降序建小堆!
void HeapSort(HPDateType* arr, int n)
{int parent = (n - 1 - 1) / 2;//建堆 --O(n)while(parent>=0){AdjustDown(arr, n, parent);--parent;}//排序 --O(nlogn)int end = n - 1;while (end>0){Swap(&arr[0], &arr[end]);//向下调整重新建堆AdjustDown(arr, end, 0);--end;}
}
int main()
{int arr[] = { 27,15,19,18,28,34,65,49,25,37 };int n = sizeof(arr) / sizeof(int);HeapSort(arr, n);for (int i = 0; i < n; ++i){printf("%d ", arr[i]);}printf("\n");
}

2、TOP-K问题
在前面堆的简单应用中我们也简单的学习了用堆的数据结构进行解决TOP-K问题,我们建立一个大堆,对堆顶元素进行删除拿到第一个数据,再重新向下调整建堆,再对堆顶元素进行删除拿到第二个数据…如此往复,便解决了TOP-K的问题。

但是一般情况下TOP-K问题的数据量都比较大,我们再利用上面的方法可能就不太行了,例如从100亿个数据中选择10个最大的,假设全是整数,那么需要400亿字节,而1G≈10亿字节,我们用数组存储这100亿个数就需要40G的内存,这显然内存不足,于是我们就需要把这么多的数据放进硬盘中了,利用文件读取来读取数据,可是硬盘中的数据并不能建堆,于是我们就要考虑其他的算法了。
我们可以建立一个K(K为要想要选取的数的个数)个数据的小堆,从文件中读取数据与堆顶的元素进行比较,如果大于堆顶元素就替换掉堆顶元素,然后向下调整,重新建立小堆,这样经过遍历所有数后,想要的K个数就在小堆里面!
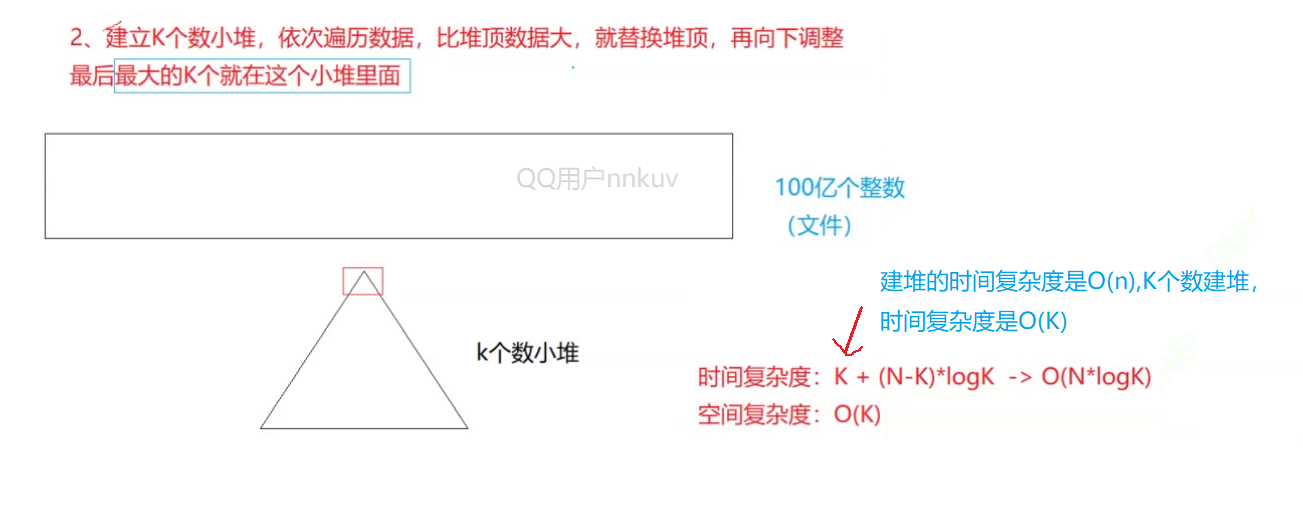
代码示例
int main()
{//选最大的5个数int randK = 5;//打开文件FILE* pfin = fopen("data.txt", "w");if (NULL == pfin){perror("fopen fail:");return;}//设置随机种子srand(time(NULL));int val = 0;for (int i = 0; i < 500; i++){//插入5个明显更大的数据,方便判断TOP-K结果是否正确if (i != 0 && i % 7 == 0 && randK > 0){fprintf(pfin, "%d ", 1000 + i);randK--;continue;}//造500个随机数val = rand() % 1000;fprintf(pfin, "%d ", val);}//关闭文件fclose(pfin);//以读的方式打开文件FILE* pfout = fopen("data.txt", "r");if (NULL == pfout){perror("fopen fail:");return;}//取5个数建立小堆int min_heap[5];for (int i = 0; i < 5; i++){fscanf(pfout, "%d", &min_heap[i]);}for (int i = (5 - 1 - 1) / 2; i >= 0; --i){AdjustDown(min_heap, 5, i);}while (fscanf(pfout, "%d", &val) != EOF){if (val > min_heap[0]){min_heap[0] = val;AdjustDown(min_heap, 5, 0);}}fclose(pfout);//打印堆中的数据for (int i = 0; i < 5; i++){printf("%d ", min_heap[i]);}return 0;
}

相关文章:

【数据结构】堆的详解
本章的知识需要有树等相关的概念,如果你还不了解请先看这篇文章:初识二叉树 堆的详解一、二叉树的顺序结构及实现1、二叉树的顺序结构2、堆的概念及结构二、堆的简单实现 (以大堆为例)1、堆的定义2、堆的初始化3、堆的销毁4、堆的打印5、堆的插入6、堆顶元素的获取7…...

New Bing怼人、说谎、PUA,ChatGPT已经开始胡言乱语了
最近,来自大洋彼岸那头的ChatGPT科技浪潮席卷而来,微软将chatGPT整合搜索引擎Bing开启内测后,数百万用户蜂拥而至,都想试试这个「百事通」。 赶鸭子上架,“翻车”了? 但短短上线十几天,嵌入了…...
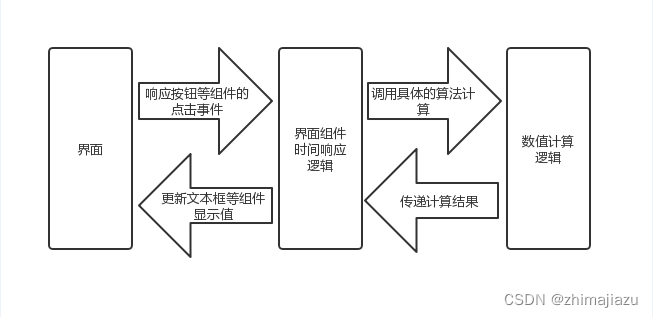
简易计算器-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-2】 简易计算器 【案例介绍】 1.案例描述 本案例要求利用Java Swing 图形组件开发一个可以进行简单的四则运算的图形化计算器。 2.运行结果 运行结果 【案例分析】 要制作一个计算器,首先要知道它由哪些部分组成,如下图所示: 一…...
)
chatGPT使用:询问简历和面试相关话题(持续更新中)
chatGPT使用:询问简历和面试相关话题 写一份Java简历,价值2万元包装上面的Java简历面试自我介绍面试简述稿包装简历的方法技巧如何进行良好的自我介绍如何写一份优秀的面试简述稿如何写一份优秀的简历如何写一份优秀的面试讲述稿如何提高面试录取率如何拿到offer写一份Java简…...

Java的 Stream流
Stream流?结合Lambda表达式,用于简化集合和数组操作的API。Stream流的一个小例子:创建一个集合,存储多个姓名,把集合中所有以"张"开头的长度为3的元素存储到一个新的集合并输出。List<String> namesne…...
FL Studio 21 中文正式版发布支持多种超个性化主题
万众期待的 FL Studio 21 版本正式发布上线,目前在紧锣密鼓的安排上线中,届时所有购买正版 FL Studio 的用户,都可以免费升级到21版! 按照惯例,本次新版也会增加全新插件,来帮助大家更好地创作。今天先给大…...

【微信小程序】-- 全局配置 -- window - 导航栏(十五)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...
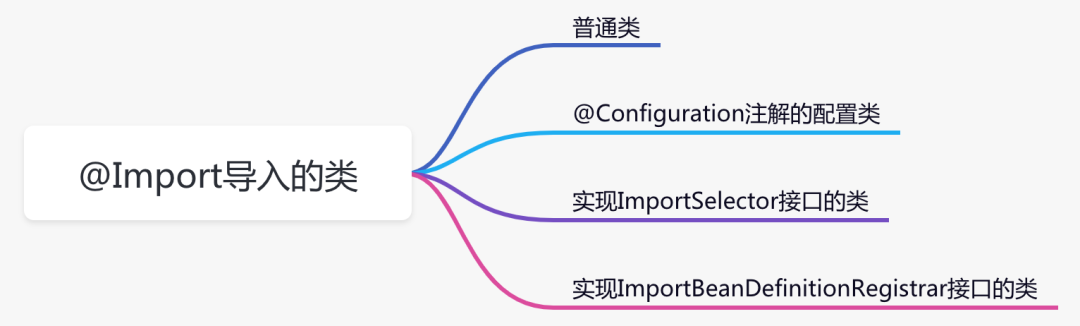
Spring中最常用的11个扩展点
前言我们一说到spring,可能第一个想到的是 IOC(控制反转) 和 AOP(面向切面编程)。没错,它们是spring的基石,得益于它们的优秀设计,使得spring能够从众多优秀框架中脱颖而出。除此之外…...

网络协议丨HTTPS是什么?
我们都知道HTTP协议,那什么是HTTPS? 我们都知道,HTTP有两个缺点——“明文”和“不安全”仅凭 HTTP 自身是无力解决的,需要引入新的 HTTPS 协议。 由于 HTTP 天生“明文”的特点,整个传输过程完全透明,任…...
Anaconda常用命令总结,anaconda、conda、miniconda的关系
Anaconda、conda、miniconda的关系 Anaconda Anaconda 是一个用于数据科学,机器学习和深度学习的开源软件包管理系统,其中包括了许多流行的 Python 包和工具Anaconda主要用于科学计算和数据分析。 conda Conda 是 Anaconda 中的包管理器,…...

【蓝桥杯入门到入土】最基础的数组你真的掌握了吗?
文章目录一:数组理论基础二:数组知识点总结三:数组这种数据结构的优点和缺点是什么?四:实战解题1. 移除元素暴力解法双指针法2.有序数组的平方暴力解法双指针法最后说一句一:数组理论基础 首先要知道数组在…...
)
Java Set系列集合(Collections集合工具类、可变参数)
目录Set系列集系概述HashSet集合元素无序的底层原理:哈希表HashSet集合元素去重复的底层原理LinkedHashSet有序实现原理TreeSetCollection集合总结可变参数Collections集合工具类Set系列集系概述 Set系列集合特点 无序:存取顺序不一致不重复࿱…...

chromium构建原生AS项目-记录1
构建的chromium版本:待补充重要说明:so文件加载的过程文件:base_java.jar包文件路径:org.chromium.base.library_loader.LibraryLoader方法:loadAlreadyLocked(Context context)line166 :Native…...
Mybatis-Plus 开发提速器:mybatis-plus-generator-ui
Mybatis-Plus 开发提速器:mybatis-plus-generator-ui 1.简介 github地址 : https://github.com/davidfantasy/mybatis-plus-generator-ui 提供交互式的Web UI用于生成兼容mybatis-plus框架的相关功能代码,包括Entity,Mapper,Mapper.xml,Se…...

李迟2023年02月工作生活总结
本文为 2023 年 2 月工作生活总结。 研发编码 Linux Go 某工程使用到一些数据的统计,为方便,使用 map 存储数量,由于其是无序的,输出的列表顺序不固定,将其和历史版本对比不方便,所以需要将 key 排序再输…...

【Python百日进阶-Web开发-Vue3】Day542 - Vue3 商城后台 02:Windi CSS 与 Vue Router4
文章目录 一、WindiCSS 初始1.1 WindiCSS 是什么?1.2 为什么选择 Windi CSS?1.3. 基础用法1.4 集成二、简单按钮2.1 设置背景色2.2 设置字体颜色和上下左右padding2.3 设置圆角2.4 鼠标悬浮,颜色加深2.5 鼠标划入动画2.6 设置阴影2.7 @apply 抽离class代码到 style 块中三、…...
Jupyter Lab | “丢下R,一起来快乐地糟蹋服务器!”
写作前面 工具永远只是为了帮助自己提升工作效率 —— 沃兹基硕得 所以说,为什么要使用jupyterlab呢?当然是因为基于服务器来处理数据就可以使劲造了,而且深切地感觉到,“R这玩意儿是人用的吗”。 jupyter-lab | mamba安装以及…...
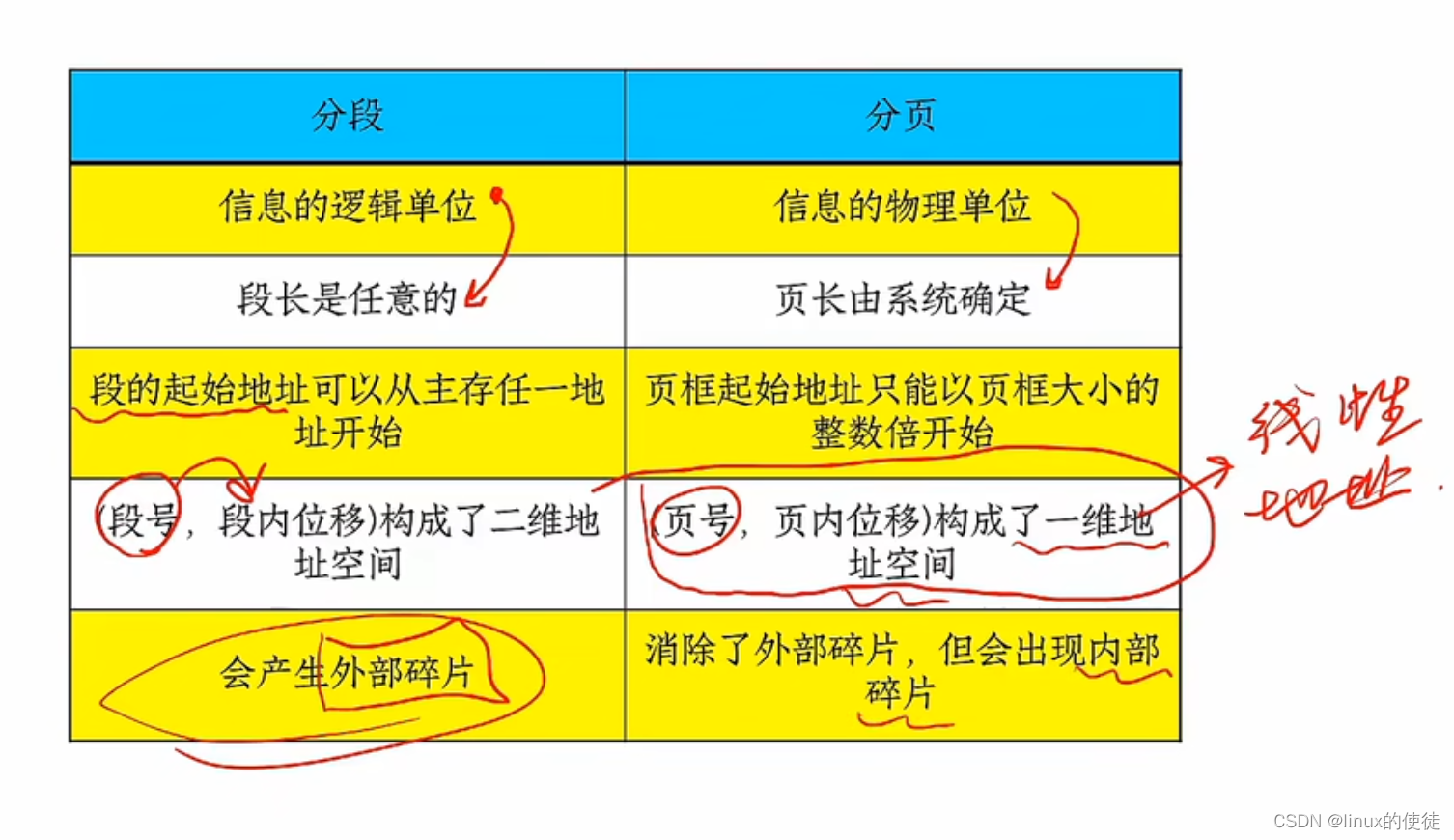
分页与分段
前面我们分析了虚拟地址和物理地址 我们这里进行一个简单的分析 这个是程序运行时的地址映射 那么这些碎片,我们现在的操作系统究竟如何处理呢? 我们再引入一个实际问题 我们如何把右边的进程p塞入左边的内存空间里面 有一种方法将p5kill掉ÿ…...
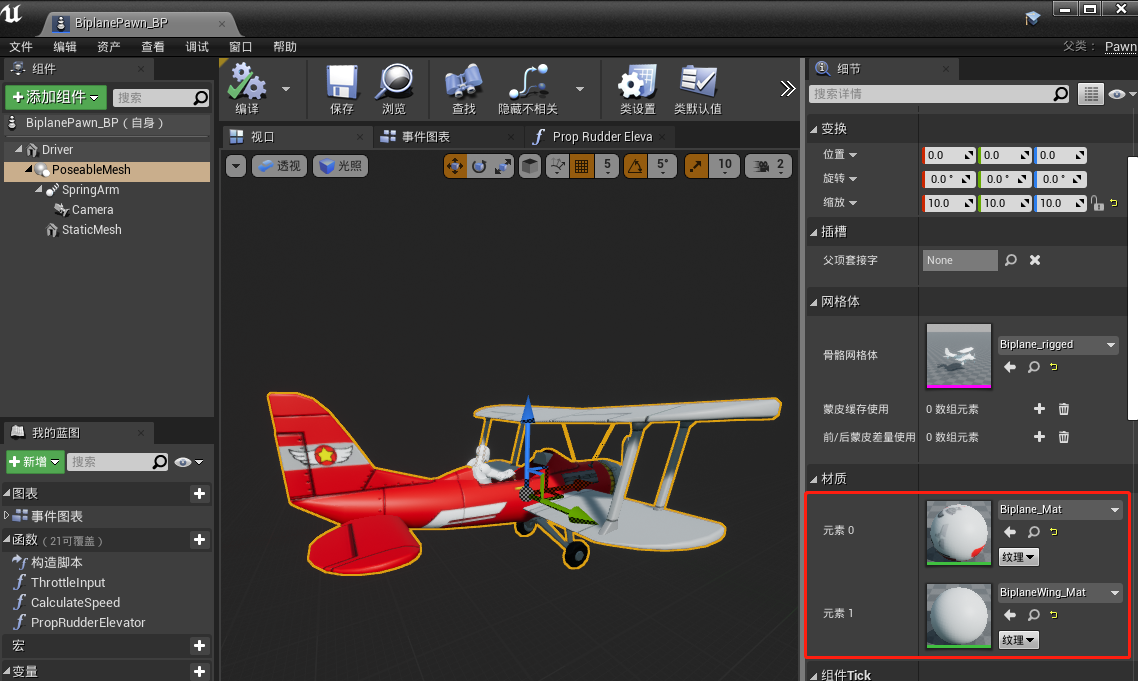
【UE4 】制作螺旋桨飞机
一、素材资源链接:https://pan.baidu.com/s/1xPVYYw05WQ6FABq_ZxFifg提取码:ivv8二、课程视频链接https://www.bilibili.com/video/BV1Bb411h7qw/?spm_id_from333.337.search-card.all.click&vd_source36a3e35639c44bb339f59760641390a8三、最终效果…...

五.家庭:亲情背后有理性
5.1经济学帝国主义【单选题】以下属于经济学研究范围的是( )。A、约束最优化B、稀缺资源配置C、价格竞争与非价格竞争D、以上都对我的答案:D【多选题】为何有学科分类?A、分工B、专业化C、累积创新D、科技进步我的答案:ABCD【判断…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
