js用到的算法
1.对象数组中,对象中有对象,数组根据对象中的对象打平
[{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '固定收益类',rowName2: '交易类',rowName3: '次级'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '固定收益类',rowName2: '交易类',rowName3: '中期'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '权益类',rowName2: '',rowName3: 'A股'},{indexValueMap: { '68443': 0, '68457': 0 },rowName1: '权益类',rowName2: '',rowName3: '港股'}
]
[{ '68443': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '次级' },{ '68457': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '次级' },{ '68443': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '中期' },{ '68457': 0, rowName1: '固定收益类', rowName2: '交易类', rowName3: '中期' },{ '68443': 0, rowName1: '权益类', rowName2: '', rowName3: 'A股' },{ '68457': 0, rowName1: '权益类', rowName2: '', rowName3: 'A股' },{ '68443': 0, rowName1: '权益类', rowName2: '', rowName3: '港股' },{ '68457': 0, rowName1: '权益类', rowName2: '', rowName3: '港股' }
]方法:使用JavaScript的数组方法 .reduce() 来解决这个问题。.reduce() 方法在数组中的每个元素上执行一个reducer函数,并返回一个单一的输出值。
这段代码首先将原始数组array中的每一项curr中的indexValueMap的键值对作为对象推入累积器数组acc中。然后将每一项的其他属性rowName1, rowName2, rowName3添加到这个对象中。最后返回累积器数组,得到的结果就是你希望得到的形式。
let array = [ // ...你的原始数组
]; let result = array.reduce((acc, curr) => { for (let key in curr.indexValueMap) { acc.push({ [key]: curr.indexValueMap[key], rowName1: curr.rowName1, rowName2: curr.rowName2, rowName3: curr.rowName3, }); } return acc;
}, []); console.log(result);function flattenArray(arr: any) {let result: any = [];arr.forEach((obj: any) => {let indexValueMap = obj.indexValueMap;let newObj = { ...obj }delete newObj.indexValueMaplet newArr = []for (let key in indexValueMap) {let tempObj = JSON.parse(JSON.stringify(newObj))tempObj[key] = indexValueMap[key]newArr.push(tempObj)}result.push(newArr)})result = result.flat(1)return result;
}2.树形结构数组,其中层级不一定,获取数组中最大的层级
这个问题的解决需要一个深度优先遍历(DFS)的算法。
getMaxLevel函数会遍历给定的数据数组,并使用深度优先搜索找出最大的层级。它在遍历每个节点时都会检查是否存在children属性,如果存在,则层级加一,并对每个子节点进行同样的处理。在遍历过程中,它会持续更新最大的层级数。最后,它会返回最大的层级数。
需要注意的是,这个函数假设给定的数据数组的结构是一致的,即每个对象都有labelName、children和indexValueMap属性,且children是一个对象数组。如果数据结构可能有所不同,你可能需要添加一些错误处理代码。
function getMaxLevel(data) { let maxLevel = 0; function dfs(node, level) { if (node.children) { level++; for (let child of node.children) { dfs(child, level); } } maxLevel = Math.max(maxLevel, level); } for (let item of data) { dfs(item, 0); } return maxLevel;
} let data = [/* Your data */];
console.log(getMaxLevel(data));3.对象数组中,去除key值包含某个字符串的元素
let flatArr = getFlattenArr(arr, 'indexMap')//根据indexValueMao展开表格前去掉多余数据
function getFlattenArr(arr: any, delKey: any) {arr.map((obj: any) => {const keys = Object.keys(obj);keys.forEach((k) => {if (k.startsWith(delKey)) {delete obj[k]}})return obj});return arr
}4.通过两个栈实现一个队列
栈和队列是两种常见的数据结构。栈遵循 LIFO(后进先出)原则,而队列遵循 FIFO(先进先出)原则。可以通过两个栈来实现一个队列。
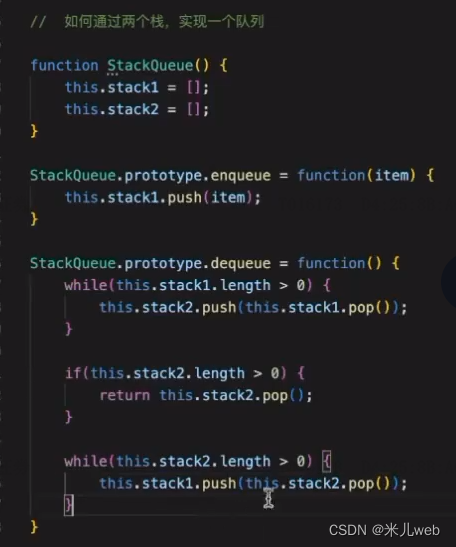
class Queue { constructor() { this.stack1 = []; this.stack2 = []; } enqueue(element) { this.stack1.push(element); } dequeue() { if (this.stack2.length === 0) { while (this.stack1.length > 0) { this.stack2.push(this.stack1.pop()); } } return this.stack2.pop(); }
}while() 是一个函数,而不是一个语句。它用于在满足某个条件的情况下反复执行代码块。
while() 函数的语法如下:
while (condition) { // code to be executed while the condition is true
}在这个语法中,condition 是一个表达式,它会在每次循环迭代之前进行评估。如果 condition 的值为 true,则执行循环体内的代码;否则,循环会终止。
5.二叉树中,有三种常见的遍历方式:前序遍历、中序遍历和后序遍历。
- 前序遍历 (Preorder Traversal)
在前序遍历中,首先访问根节点,然后递归地访问左子树,最后访问右子树。
function preorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; result.push(node.value); // 访问根节点 helper(node.left); // 递归访问左子树 helper(node.right); // 递归访问右子树 } helper(root); return result;
}- 中序遍历 (Inorder Traversal)
在中序遍历中,首先递归地访问左子树,然后访问根节点,最后递归地访问右子树。
function inorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; helper(node.left); // 递归访问左子树 result.push(node.value); // 访问根节点 helper(node.right); // 递归访问右子树 } helper(root); return result;
}- 后序遍历 (Postorder Traversal)
在后序遍历中,首先递归地访问左子树,然后递归地访问右子树,最后访问根节点。
function postorderTraversal(root) { const result = []; function helper(node) { if (node === null) return; helper(node.left); // 递归访问左子树 helper(node.right); // 递归访问右子树 result.push(node.value); // 访问根节点 } helper(root); return result;
}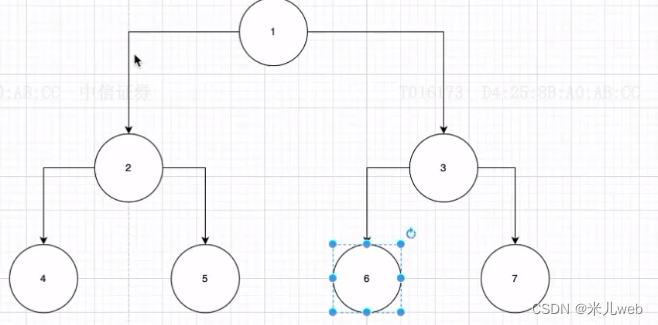
前序:1245367
中序:4251637
后序:4526731
四大算法:分治、回溯、贪心、动规
分治法是一种将问题划分为小规模子问题的算法设计策略。分治法通过将问题划分为更小的部分,然后分别解决这些子问题,最后将这些子问题的解合并以得到原始问题的解。分治法的主要步骤包括:分解、解决、合并。
一个著名的使用分治法设计的算法是快速排序。在快速排序中,我们选择一个基准元素,然后将数组划分为两个子数组:一个包含所有小于基准的元素,另一个包含所有大于或等于基准的元素。然后我们对这两个子数组递归地应用快速排序。
回溯法是一种通过探索所有可能的候选解来找出所有的解的算法。回溯算法会检查每一步决策是否正确,并“回溯”或撤销先前的决策,然后继续探索其他可能的决策。这种算法通常用于解决组合优化问题,如八皇后问题、图的着色问题、旅行商问题等。
一个典型的回溯算法的实现通常包括:一个递归函数,该函数通过调用自身来处理子问题,以及一个“剪枝”函数,该函数用于排除那些不可能是最优解的候选解。
ex1:回溯法-归并排序
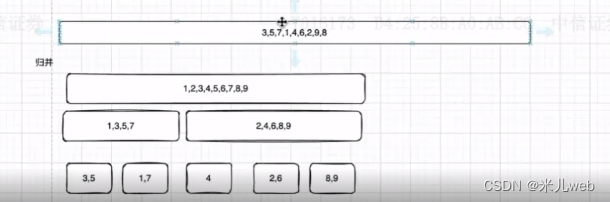
Math.floor() 是JavaScript的一个内置函数,用于返回小于或等于一个给定数字的最大整数。换句话说,它向下取整。
Math.floor(3.7); // 返回 3
Math.floor(3.8); // 返回 3
Math.floor(-3.7); // 返回 -4
Math.floor(-3.8); // 返回 -4
function mergeSort(arr){ if(arr.length === 1) return arrconst midIdx = Math.floor(arr.length /2) return merge(mergeSort(arr.slice(0,midIdx)), mergeSort(arr.slice(midIdx)))}// [1,3,5,7]--[2,4,6,8,9]function merge(leftArr, rightArr) {let temp = []while(leftArr.length>0 && rightArr.length>0){if(leftArr[0]<rightArr[0]){temp.push(leftArr.shift())}else{temp.push(rightArr.shift())}} return temp.concat(leftArr).concat(rightArr) }let arr = [1,8,3,9,5,4,6,2,7]console.log(mergeSort(arr)) //[1,2,3,4,5,6,7,8,9]
function mergeSort(arr) { // 如果数组只有一个元素,直接返回 if (arr.length <= 1) { return arr; } // 将数组分成两部分,分别进行递归排序 const mid = Math.floor(arr.length / 2); const left = arr.slice(0, mid); const right = arr.slice(mid); return merge(mergeSort(left), mergeSort(right));
} function merge(left, right) { // 合并两个有序数组 const result = []; let i = 0; let j = 0; while (i < left.length && j < right.length) { if (left[i] < right[j]) { result.push(left[i]); i++; } else { result.push(right[j]); j++; } } // 将剩余元素添加到结果数组中 while (i < left.length) { result.push(left[i]); i++; } while (j < right.length) { result.push(right[j]); j++; } return result;
}ex2:分治-求平方根
ex3:分治-快排
相关文章:

js用到的算法
1.对象数组中,对象中有对象,数组根据对象中的对象打平 [{indexValueMap: { 68443: 0, 68457: 0 },rowName1: 固定收益类,rowName2: 交易类,rowName3: 次级},{indexValueMap: { 68443: 0, 68457: 0 },rowName1: 固定收益类,rowName2: 交易类,rowName3: 中…...

【科技素养】蓝桥杯STEMA 科技素养组模拟练习试卷9
1、商标也属于知识产权的一种。一个商标在注册之后,将会在()的时间受到保护 A、20 年内 B、50 年内 C、直至注册人去世 D、10 年内 答案:D 2、人类史上第一位进入太空的宇航员是(),他/她是…...

如何使用抖音直播调试入口扫码进行调试
使用抖音直播调试入口扫码进行调试的步骤如下: 确保你已经安装了抖音调试助手。打开调试助手,并在主界面点击“连接”按钮。在连接向导页面,根据提示连接你的抖音直播间。请确保你已经获取了直播间的token和scheme。连接成功后,你…...

AI智能人机对话小程序系统源码 附带完整的搭建教程
移动互联网的普及和快速发展,小程序已经成为了一种非常流行的应用形态。小程序具有即用即走、轻量级的特点,非常适合用于提供各种便捷服务。下面罗峰来给大家分享一款AI智能人机对话小程序系统源码,带有完整的搭建教程。 以下是部分代码示例…...

【腾讯云云上实验室】用向量数据库在金融信数据库分析中的实战运用
一、前言 这篇文章将带领读者探索数据库的多样化解决方案及其演进历程,特别关注向量数据库的重要性和在实际项目中的应用。 通过深入剖析腾讯云向量数据库及其在金融信用数据库分析中的实战运用,为读者提供全面而实用的指南,帮助他们理解、…...

2015年五一杯数学建模A题不确定性条件下的最优路径问题解题全过程文档及程序
2015年五一杯数学建模 A题 不确定性条件下的最优路径问题 原题再现 目前,交通拥挤和事故正越来越严重的困扰着城市交通。随着我国交通运输事业的迅速发展,交通“拥塞”已经成为很多城市的“痼疾”。在复杂的交通环境下,如何寻找一条可靠、快…...
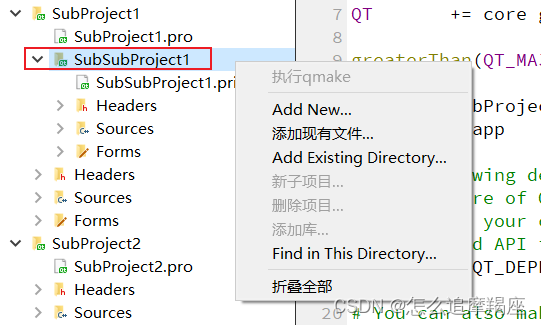
5、Qt:项目中包含多个子项目(.pro)/子模块(.pri)
一、说明: 在进行项目开发过程中,会涉及子项目/子模块的问题 Qt中使用TEMPLATE subdirs添加多个子项目;子项目可以单独编译生成可执行文件(exe)或者动态链接库(dll)等,供其他模块…...

Facebook的特点优势
Facebook作为全球最大的社交媒体平台之一,同时也是最受欢迎的社交网站之一,Facebook具有许多独特的特点和优势。本文小编将说一些关于Facebook的特点及优势。 1、全球化 Facebook拥有数十亿的全球用户,覆盖了几乎所有国家和地区。这使得人们…...
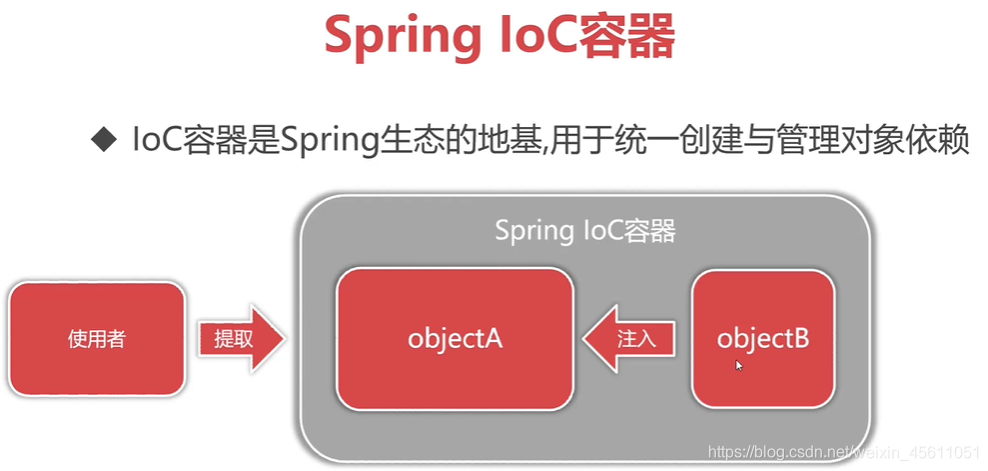
Spring框架体系及Spring IOC思想
目录 Spring简介Spring体系结构SpringIOC控制反转思想自定义对象容器Spring实现IOCSpring容器类型容器接口容器实现类对象的创建方式使用构造方法使用工厂类的方法使用工厂类的静态方法对象的创建策略对象的销毁时机生命周期方法获取Bean对象的方式通过id/name获取通过类型获取…...

WT588F02B-8S语音芯片:16位DSP技术引领个性化功能产品新时代
随着科技的快速发展,语音芯片作为人机交互的核心组件,在各个领域的应用越来越广泛。唯创知音推出的WT588F02B-8S语音芯片,以其强大的16位DSP技术和丰富的内置资源,正成为行业内的翘楚。 首先,唯创知音WT588F02B-8S是一…...
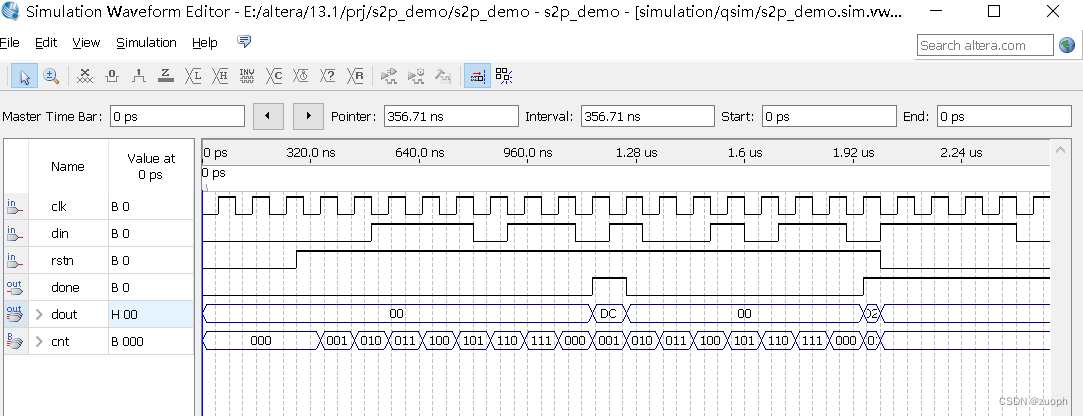
数字逻辑电路基础-时序逻辑电路之移位寄存器
文章目录 一、移位寄存器定义二、verilog源码三、仿真结果 一、移位寄存器定义 移位寄存器定义 A shift register is a type of digital circuit using a cascade of flip flops where the output of one flip-flop is connected to the input of the next. 移位寄存器是一种将…...
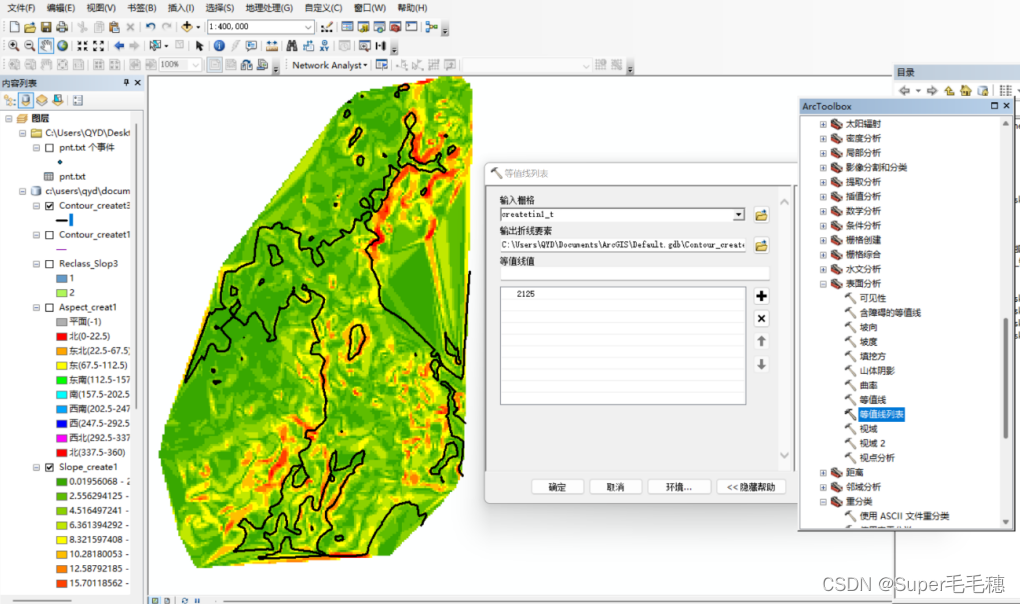
DEM分析
一、实验名称: DEM分析 二、实验目的: 通过本实验练习,掌握DEM的建立与应用基本方法。 三、实验内容和要求: 实验内容: 利用ARCGIS软件相关分析工具及实验数据,创建DEM,并计算相应坡度的区…...

全面探讨HTTP协议从0.9到3.0版本的发展和特点
前言: 最近的几场面试都问到了http的相关知识点,博主在此结合书籍和网上资料做下总结。本篇文章讲收录到秋招专题,该专栏比较适合刚入坑Java的小白以及准备秋招的大佬阅读。 如果文章有什么需要改进的地方欢迎大佬提出,对大佬有帮…...
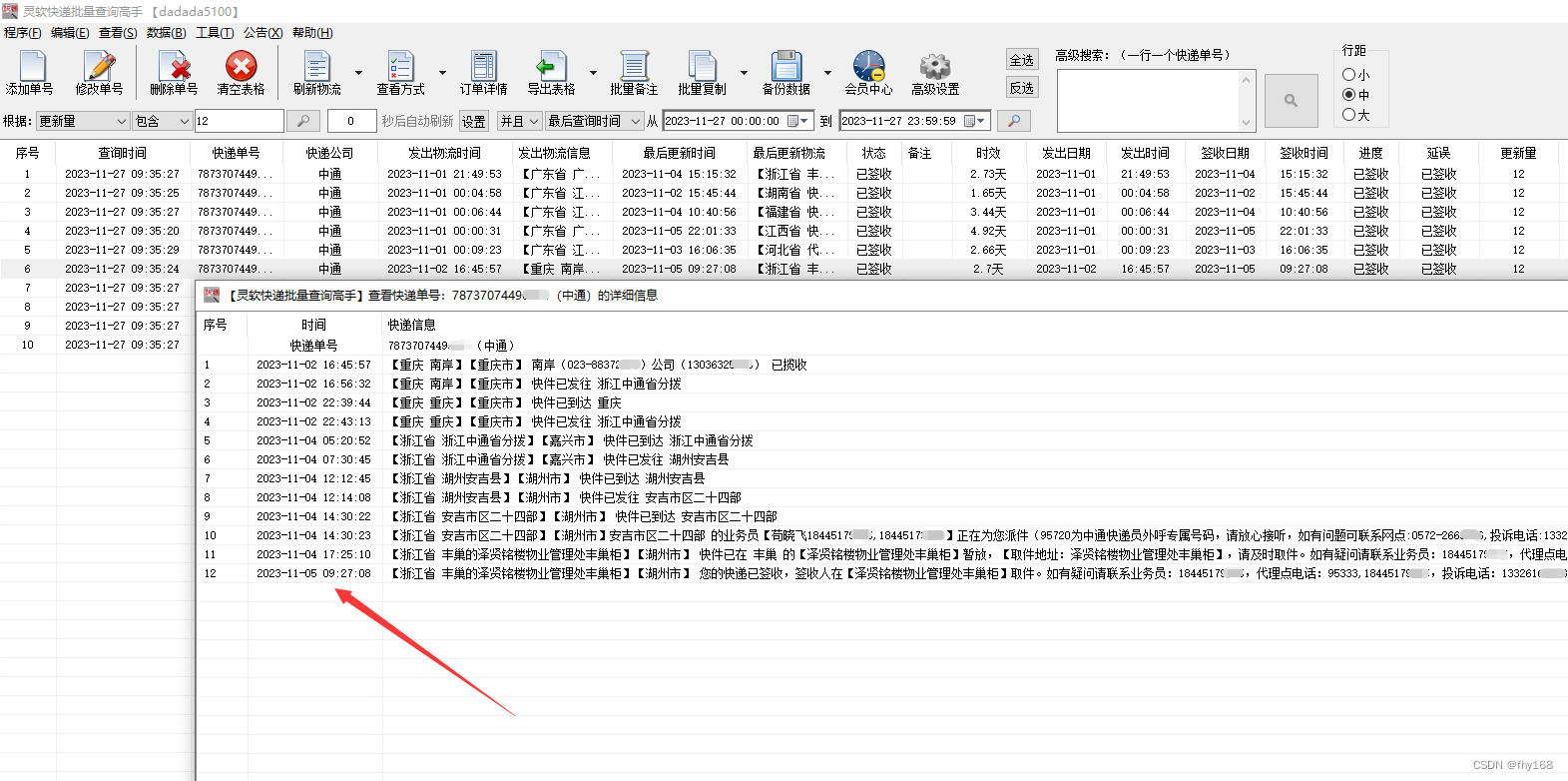
中通快递查询入口,根据物流更新量筛选出需要的单号记录
批量中通快递单号的物流信息,根据物流更新量将需要的单号记录筛选出来。 所需工具: 一个【快递批量查询高手】软件 中通快递单号若干 操作步骤: 步骤1:运行【快递批量查询高手】软件,并登录 步骤2:点击主…...
Arraylist案例
Arraylist是使用最频繁的一个集合,它与数组类似,不同之处在于它可以动态改变长度,不够了可以扩容。 案例: 我的思考: 首先多个菜品信息可以用Arraylist 来存储,那我们需要再创建一个菜品类Food࿰…...

『heqingchun-Ubuntu系统+x86架构+配置编译安装使用yolov5-6.0+带有TensorRT硬件加速+C++部署』
Ubuntu系统x86架构配置编译安装使用yolov5-6.0带有TensorRT硬件加速C部署 一、准备文件 1.yolov5-6.0.zip 官网下载 网址: https://github.com/ultralytics/yolov5/tree/v6.0操作: 点击"Code"下的"Download ZIP" 下载得到yolov5…...

优秀的员工成为公司的管理者之后,为何表现平庸?因为他们缺乏这些思维
在企业的实践中,我们发现平时能力最强的员工,在被提拔到管理层之后就慢慢变得平庸了,再也不是以前那个无所不能的“企业能人”了,甚至在一些事情的处理上还会有些笨拙。面对这种情况,我们一定会感觉很疑惑,…...

MySQL简单介绍
简单了解MySQL MySQL语句分类 SQL语句分类 DDL:数据定义语句 create表,库.….] DML:数据操作语句 [增加insert,修改 update,删除delete] DQL:数据查询语句 [select] DCL:数据控制语句 …...

【开源】基于JAVA的天然气工程业务管理系统
项目编号: S 021 ,文末获取源码。 \color{red}{项目编号:S021,文末获取源码。} 项目编号:S021,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块三、使用角色3.1 施工人员3.2 管理员 四…...
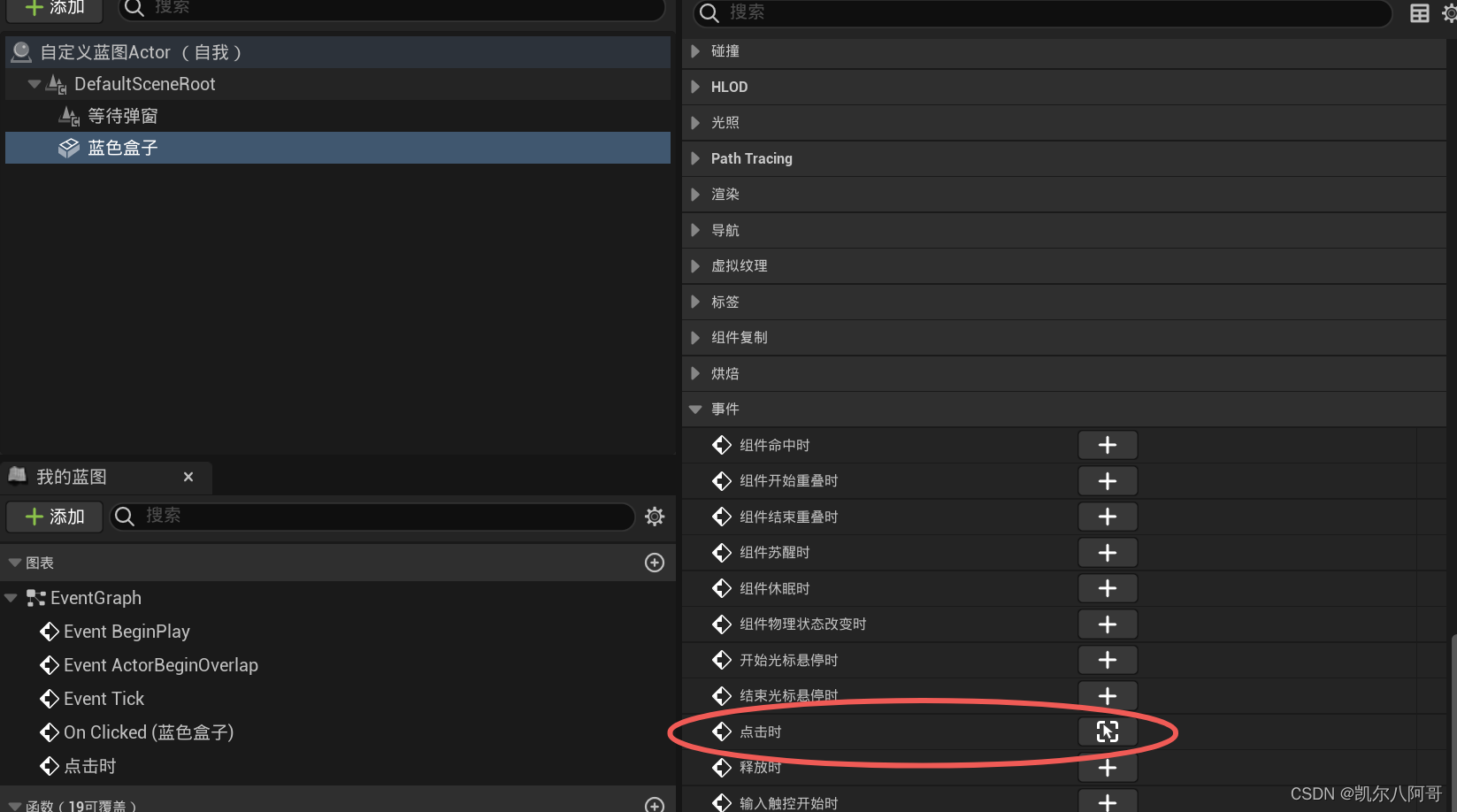
虚幻学习笔记—点击场景3D物体的两种处理方式
一、前言 本文使用的虚幻引擎为5.3.2,两种方式分别为:点击根物体和精准点击目标物体。 二、实现 2.1、玩家控制器中勾选鼠标点击事件:这一步很重要,如图2.1.1所示:在自定义玩家控制器中勾 图2.1.1 选该项,…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

[10-1]I2C通信协议 江协科技学习笔记(17个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17...
