【二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)二叉排序树的操作----插入生成删除】
文章目录
- 二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)
- 二叉树的查找分析
- 二叉排序树的操作----插入
- 二叉排序树的操作----生成
- 二叉排序树的操作----删除
二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)
【算法思想】
(1)若二叉排序树为空,则查找失败,返回空指针。
(2)若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
①若key等于T->data.key,则查找成功,返回根结点地址;
②若key小于T->data.key,则进一步查找左子树。
③若key大于T->data.key,则进一步查找右子树。
二叉排序树的定义:
typedef struct {KeyType key;//关键字项
};typedef struct BSTNode {ElemType data;struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;
二叉排序树的递归查找:
BSTree SearchBST(BSTree T, KeyType key) {//在根指针T所指向的二叉排序树中递归的查找关键字key的数据元素。//若查找成功,则返回指向该元素的指针,否则返回空指针。if ((!T) || key == T->data) {return T;}else if(key<T->data){ return SearchBST(T->lchild,key);}else {return SearchBST(T->rchild, key);}
}
二叉树的查找分析
二叉排序树上查找某关键字等于给定值的结点的过程,其实就是走了一条从根到该结点的路径。
比较的关键次数=该结点的层次数=最多的比较次数=树的深度
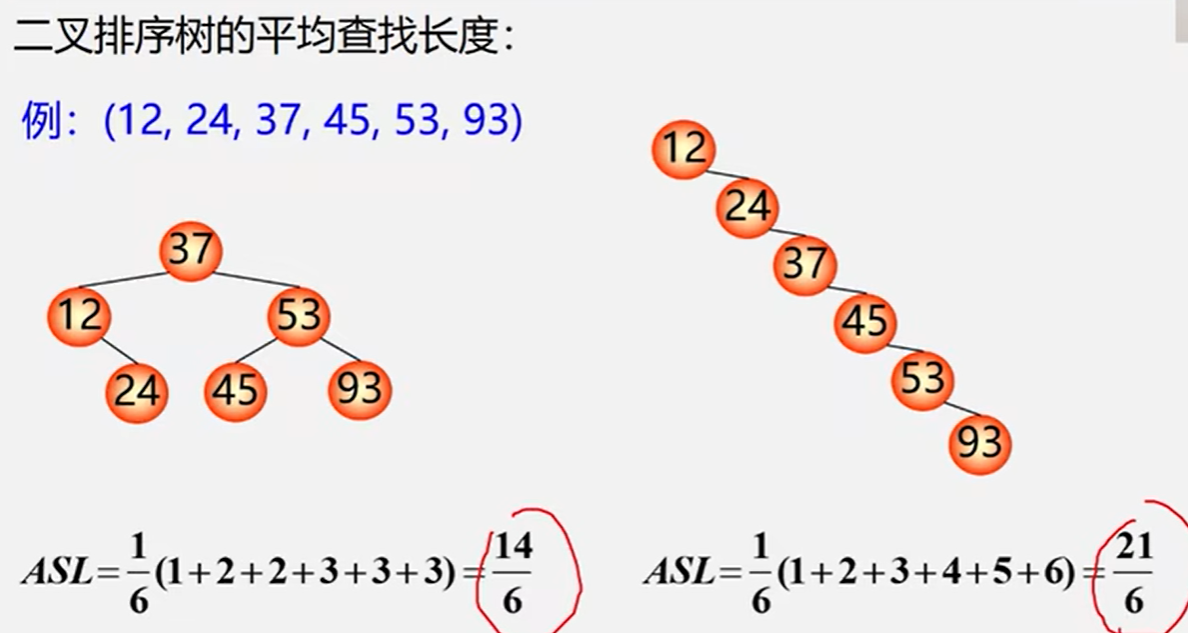
含有n个结点的二叉排序树的平均查找长度和树的形态有关。
如何提高形态不均衡的二叉排序树的查找效率?
做“平衡化”处理,即尽量的让二叉树的形态均衡。----->平衡二叉树。
二叉排序树的操作----插入
- 若二叉排序树为空,则插入结点作为根结点到空树中。
- 否则,继续在其左,右子树上查找。
- 树中已有,不再插入。
- 树中没有
- 查找直至某个叶子结点的左子树或右子树为空,则插入结点应为叶子结点的左孩子或右孩子。
void InsertBST(BSTree& T, ElemType e) {if (!T) {BSTree S;S = new BSTNode;S->data = e;S->lchild = S->rchild = NULL;//新结点*S作为叶子结点T = S;}else if (T->data > e) {InsertBST(T->lchild, e);//将*S插入左子树}else if(T->data < e){InsertBST(T->rchild, e);//将*S插入右子树}
}
【算法分析】
二叉排序树的基本过程是查找,所以时间复杂度同查找一样,是O(log2n),2是底数。
二叉排序树的操作----生成
从空树出发,经过一系列的查找,插入操作之后,可生成某一棵二叉排序树。

一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
插入的结点均为叶子结点,故无需移动其他结点。
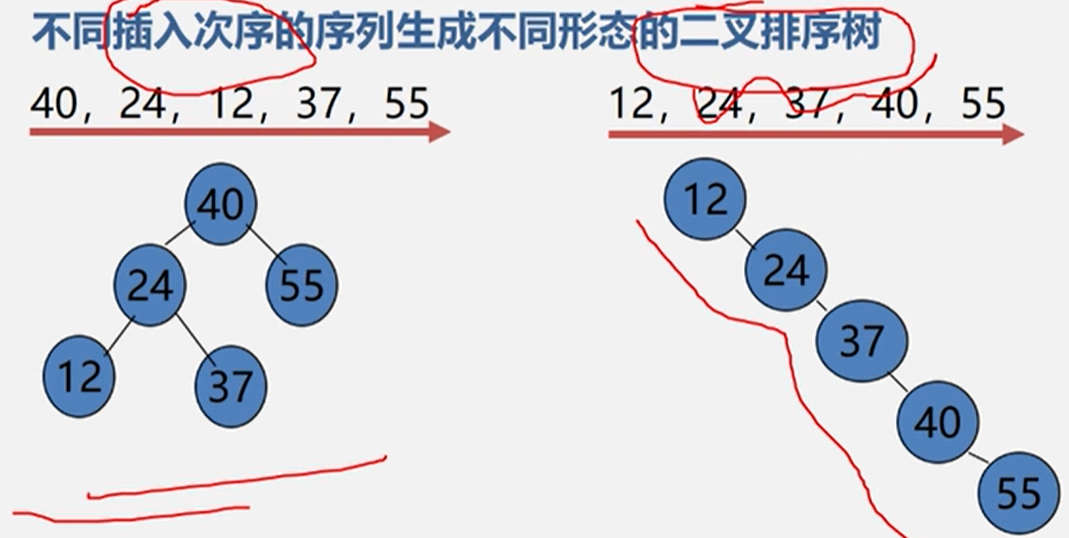
关键字的顺序不同,建立的不同二叉排序树。
void CreateBST(BSTree& T) {//一次读入关键字为key的结点,将相应的节点插入到二叉排序树T中T = NULL;int e;cin >> e;int ENDFLAG = 0;while (T->data != ENDFLAG) {InsertBST(T, e);//将此结点插入到二叉排序树中去cin >> e;}
}
【算法分析】
假设有n个结点,则需要n次插入操作,而插入一个结点的算法的时间复杂度O(nlog2n),2为底数。
二叉排序树的操作----删除
(1)被删除的结点是叶子结点:直接删去该结点。
其双亲结点中相应的指针域的值改为“空”。
(2)被删除的结点只有左子树或者右子树,用其左子树或右子树替换它。(结点替换)。
其双亲结点相应的指针域的值改为“指向被删除结点的左子树或者右子树”。
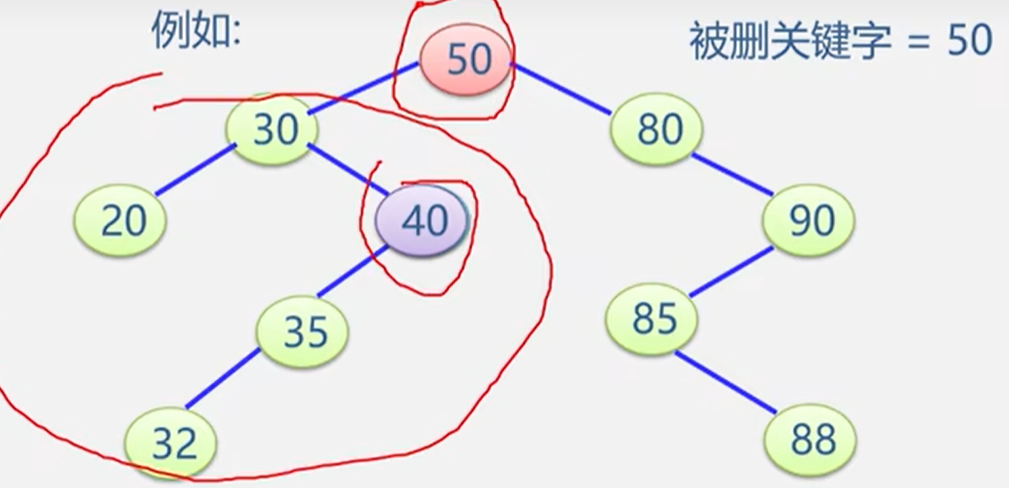
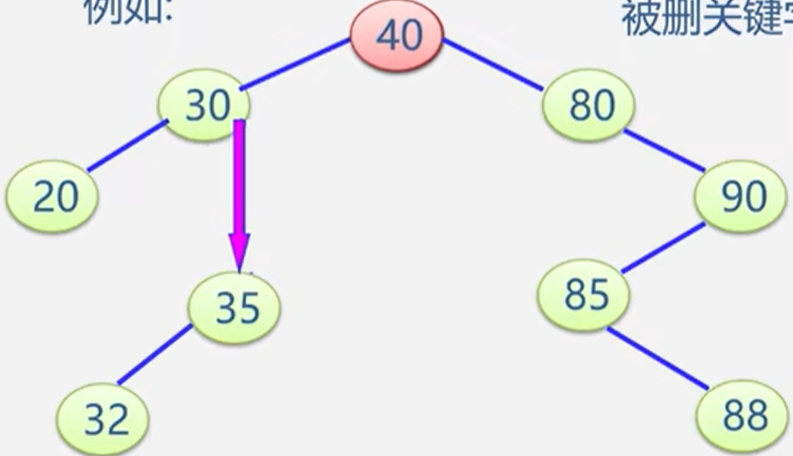
(3)被删除的结点既有左子树,又有左子树。
- 以其中序前驱值替换之(值替换),然后再删除该前驱结点。前驱是左子树中最大的结点。
void DeleteBST(BSTree& T, KeyType key) {//从二叉排序树中删除关键字等于key的结点BSTree p = T;BSTree q,s;BSTree f = NULL;//初始化//下面的while循环是从根结点开始找key的遍历过程while (p) {if (p->data == key) {break;}else if (p->data > key) {p = p->lchild;}else {p = p->rchild;}}if (!p) {return;}q = p;if ((p->lchild) && (p->rchild)){//若被删的结点的左子树,右子树都不为空s = p->lchild;//在*p的左子树继续查找其前驱结点,即最右下结点while (s->rchild){q = s; s = s->rchild;//向右到尽头}p->data = s->data;//s指向被删结点的前驱if (q != p) {q->rchild = s->rchild;//重接*q的右子树}else {q->lchild = s->lchild;//重接*q的左子树}delete s;return;}else if (!p->rchild) {p = p->lchild;//被删结点*p无右子树,只需接起左子树}else if (!p->lchild) {p = p->rchild;//被删结点*p无左子树,只需接起右子树}if (!f) {T = p;//被删结点的为根结点}else if (q == f->lchild) {f->lchild = p;//挂接到*f的左子树位置}else {f->rchild = p;//挂接到*f的右子树位置}delete q;
}
总代码
#include<iostream>
using namespace std;#define KeyType int
#define ElemType inttypedef struct {KeyType key;//关键字项
};typedef struct BSTNode {ElemType data;struct BSTNode* lchild, * rchild;//左右孩子指针
}BSTNode,*BSTree;BSTree SearchBST(BSTree T, KeyType key) {//在根指针T所指向的二叉排序树中递归的查找关键字key的数据元素。//若查找成功,则返回指向该元素的指针,否则返回空指针。if ((!T) || key == T->data) {return T;}else if(key<T->data){ return SearchBST(T->lchild,key);}else {return SearchBST(T->rchild, key);}
}void InsertBST(BSTree& T, ElemType e) {if (!T) {BSTree S;S = new BSTNode;S->data = e;S->lchild = S->rchild = NULL;//新结点*S作为叶子结点T = S;}else if (T->data > e) {InsertBST(T->lchild, e);//将*S插入左子树}else if(T->data < e){InsertBST(T->rchild, e);//将*S插入右子树}
}void CreateBST(BSTree& T) {//一次读入关键字为key的结点,将相应的节点插入到二叉排序树T中T = NULL;int e;cin >> e;int ENDFLAG = 0;while (T->data != ENDFLAG) {InsertBST(T, e);//将此结点插入到二叉排序树中去cin >> e;}
}void DeleteBST(BSTree& T, KeyType key) {//从二叉排序树中删除关键字等于key的结点BSTree p = T;BSTree q,s;BSTree f = NULL;//初始化//下面的while循环是从根结点开始找key的遍历过程while (p) {if (p->data == key) {break;}else if (p->data > key) {p = p->lchild;}else {p = p->rchild;}}if (!p) {return;}q = p;if ((p->lchild) && (p->rchild)){//若被删的结点的左子树,右子树都不为空s = p->lchild;//在*p的左子树继续查找其前驱结点,即最右下结点while (s->rchild){q = s; s = s->rchild;//向右到尽头}p->data = s->data;//s指向被删结点的前驱if (q != p) {q->rchild = s->rchild;//重接*q的右子树}else {q->lchild = s->lchild;//重接*q的左子树}delete s;return;}else if (!p->rchild) {p = p->lchild;//被删结点*p无右子树,只需接起左子树}else if (!p->lchild) {p = p->rchild;//被删结点*p无左子树,只需接起右子树}if (!f) {T = p;//被删结点的为根结点}else if (q == f->lchild) {f->lchild = p;//挂接到*f的左子树位置}else {f->rchild = p;//挂接到*f的右子树位置}delete q;
}int main() {return 0;
}```相关文章:

【二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)二叉排序树的操作----插入生成删除】
文章目录 二叉排序树(Binary Sort Tree)又称为二叉搜索树,二叉查找树,)二叉树的查找分析二叉排序树的操作----插入二叉排序树的操作----生成二叉排序树的操作----删除 二叉排序树(Binary Sort Tree…...

Verilog基础:时序调度中的竞争(二)
相关阅读 Verilog基础https://blog.csdn.net/weixin_45791458/category_12263729.html?spm1001.2014.3001.5482 作为一个硬件描述语言,Verilog HDL常常需要使用语句描述并行执行的电路,但其实在仿真器的底层,这些并行执行的语句是有先后顺序…...

云原生周刊:Kubernetes 1.29 中的删除、弃用和主要更改 | 2023.11.27
开源项目推荐 Orphaned ConfigMaps 该版本库包含一个脚本,用于识别 Kubernetes 命名空间中的孤立的配置映射。孤立的配置映射是指那些未被命名空间中的任何活动 Pod 或容器引用的配置映射。 Kubernetes Multi Cooker 该项目包含一个小型 Kubernetes 控制器&…...

深入理解计算机中的程序
目录 程序的存储 程序的编译过程 各位宝宝好,我们这次从计算机底层来讲一下程序是如何存储,编译的 程序的存储 我们拿一个最简单的程序来举个例子: #include<stdio.h> int main() {printf("hello world");return 0; } …...

uniapp视频倍速播放插件,uniapp视频试看插件——sunny-video使用文档
sunny-video视频倍速播放器 组件名:sunny-video 效果图 img1img2img3img4 平台差异说明 目前已应用到APP(安卓、iOS)、微信(小程序、H5)其它平台未测试 安装方式 本组件符合easycom规范,HBuilderX 2.5…...

【微软技术栈】与其他异步模式和类型互操作
本文内容 任务和异步编程模型 (APM)任务和基于事件的异步模式 (EAP)任务和等待句柄 .NET 中异步模式的简短历史记录: .NET Framework 1.0 引进了 IAsyncResult 模式,也称为异步编程模型 (APM) 或 Begin/End 模式。.NET Framework 2.0 增加了基于事件的…...
计算机毕业设计 基于微信小程序的“共享书角”图书借还管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

腾讯云CVM标准型SA5云服务器AMD EPYC Bergamo处理器
腾讯云服务器标准型SA5实例是最新一代的标准型实例,CPU采用AMD EPYC™ Bergamo全新处理器,采用最新DDR5内存,默认网络优化,最高内网收发能力达4500万pps。腾讯云百科txybk.com分享腾讯云标准型SA5云服务器CPU、内存、网络、性能、…...

网站要怎么进行维护和防御攻击
随着数字经济的不断发展,互联网各业都在稳步发展,但是很多站长搭建网站程序后也不知道怎么去维护网站的稳定和是否有漏洞后门等,为此德迅云安全专门为各大站长研发了网站监测产品 知道网站表现:网站监测可以帮助您了解您的网站的…...

代码随想录二刷 | 哈希表 |四数相加II
代码随想录二刷 | 哈希表 |四数相加II 题目描述解题思路 & 代码实现 题目描述 454.四数相加II 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0…...

Flutter | TextField长按时选项菜单复制、粘贴显示为英文问题解决
Flutter | TextField长按时选项菜单复制、粘贴显示为英文问题解决 问题描述: 长按TextField后,显示剪切、复制等选项为英文,如下图所示,这是因为问未设置语言本地化,我们需要进行设置。 首先在pubspec.yaml加入以下依赖…...
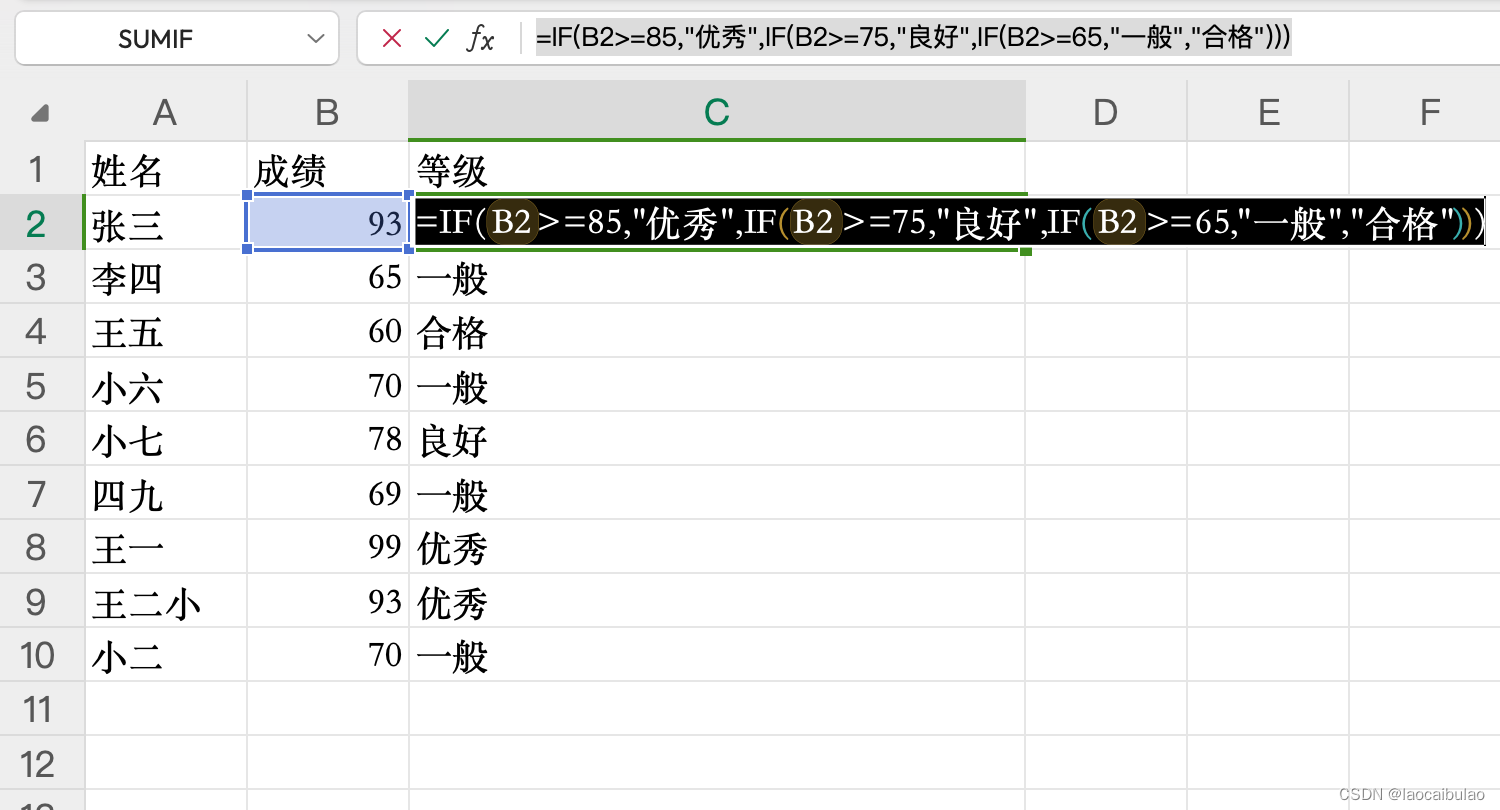
如何找出excel中两列数据中不同的值(IF函数的用法)
第一部分,举例: 例1: 如下图所示,A列和B列是需要比较的数据,C列为对比规则:IF(A2B2,"是","否") 示例图 例2:给B列的成绩评等级 C列的规则: IF(B2>85,&qu…...
C# WPF上位机开发(掌握一点c#基础)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 wpf虽然比较简单,但是最好还是要有一点c#的基础比较好。本身wpf有点类似于web开发,前端和html差不多,后端则和j…...

UIkit-UIAlertContent
简单Demo //注意!!!必须放在viewController的viewDidAppear里面,viewDidLoad里面不行 - (void)viewDidAppear:(BOOL)animated {// 创建 UIAlertControllerUIAlertController *alertController [UIAlertController alertControll…...

C语言-内存函数详解
文章目录 1. memcpy使用和模拟实现2. memmove使用和模拟实现3. memset函数的使用4. memcmp函数的使用 1. memcpy使用和模拟实现 返回类型和参数: void * memcpy ( void * destination, const void * source, size_t num );1.函数memcpy从source的位置开始向后复制…...
超越噪音,让音乐重获新生:iZotope RX 10音频降噪修复软件
在音乐制作或者音频处理的过程中,噪音往往是一个让人头痛的问题。无论是环境噪音,还是设备产生的噪音,都会对音频质量产生重大影响。而现在,我们有了iZotope RX 10,这款专业的音频降噪修复软件,可以将你从噪…...

【兔子王赠书第9期】ChatGPT进阶:提示工程入门
文章目录 写在前面ChatGPT推荐图书关键点编辑推荐内容简介推荐理由 粉丝福利写在后面 写在前面 人类一直在寻找、制造并使用工具,以扩展我们的能力,适应我们的环境,甚至超越我们的生物限制。现在,我们正站在一个历史性的分水岭之…...
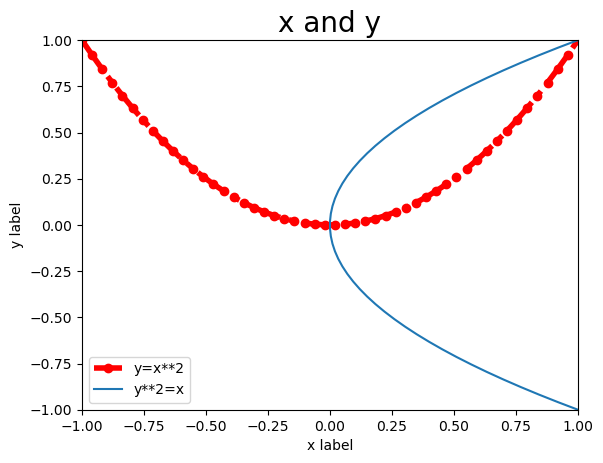
机器学习基础Matplotlib绘图
一、运行环境 学习工具:jupyter-notebookpython版本:311系统:Win11 二、什么是matplotlib? matplotlib是基于python生态开发的一个可视化绘图库,它的出现让python在数据分析及机器学习方面占了重要的一部分&#…...

【高效开发工具系列】PlantUML入门使用
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
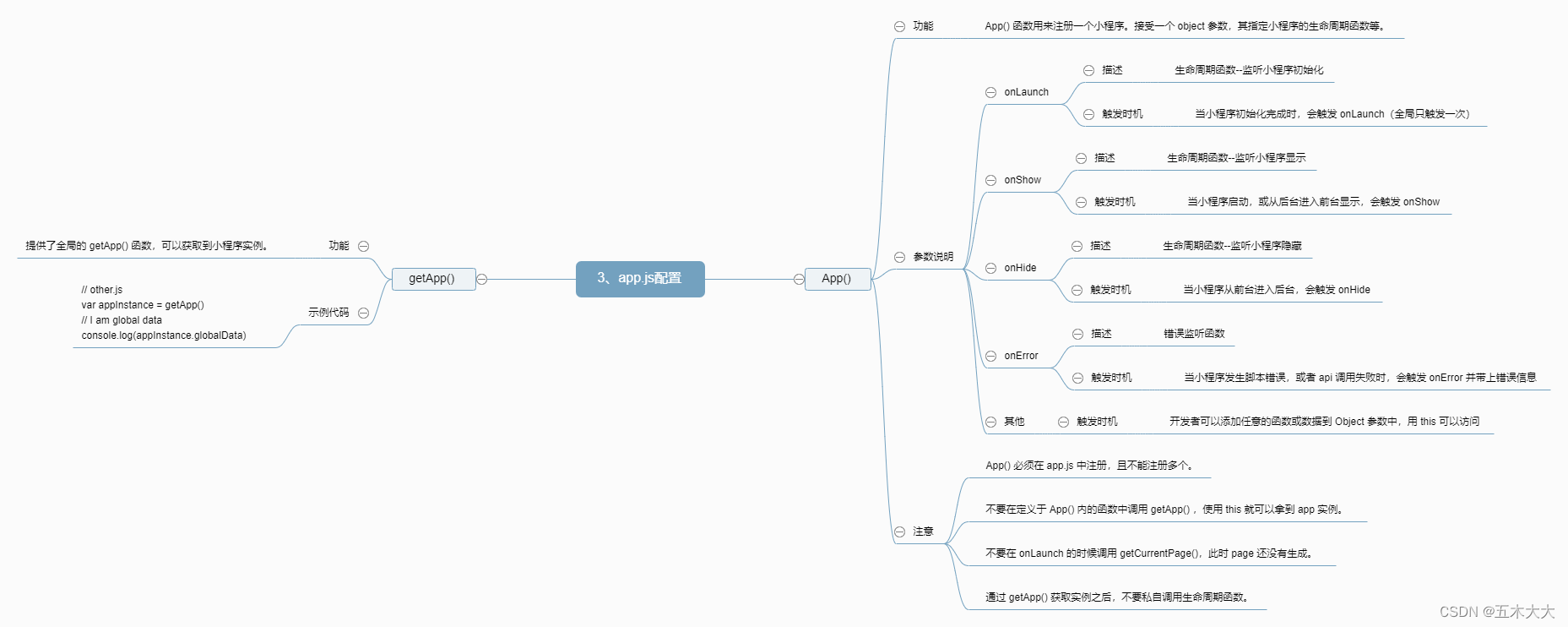
【第三节:微信小程序 3、app.js配置】微信小程序入门,以思维导图的方式展开3
目录 提供了2个函数: app.js配置 【第三节:微信小程序 3、app.js配置】微信小程序入门,以思维导图的方式展开3 提供了2个函数: app() getApp() --------------------------- app.js配置 App() 功能 Ap…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
