13-21-普通数组、矩阵
LeetCode 热题 100
文章目录
- LeetCode 热题 100
- 普通数组
- 13. 中等-最大子数组和
- 14. 中等-合并区间
- 15. 中等-轮转数组
- 16. 中等-除自身以外数组的乘积
- 17. 困难-缺失的第一个正数
- 矩阵
- 18. 中等-矩阵置零
- 19. 中等-螺旋矩阵
- 20. 中等-旋转图像
- 21. 中等-搜索二维矩阵II
本文存储我刷题的笔记。
普通数组
13. 中等-最大子数组和

我的思路
思路:从第一个非负数开始,不断向右扩大窗口更新最大值;若当前窗口为负,则继续从下一个正数开始滑动窗口。
时间96ms(50.51%),内存64.89MB(56.76%)。
class Solution {
public:int maxSubArray(std::vector<int>& nums) {int len = nums.size();// 寻找到第一个非负数int left{ -1 };int max_tmp{ nums[0] };while (left < len - 1 && nums[++left] < 0) {max_tmp = std::max(max_tmp, nums[left]);}// 向右扩大窗口,不断记录最大值,直到和为负或遍历完成int sum{ 0 };for (int i = left; i < len; i++) {sum += nums[i];max_tmp = std::max(max_tmp, sum);// 若当前和为负则重新找下一个正数if (sum < 0) {while (i < len - 1 && nums[++i] < 0) {}if (i == len - 1) {return std::max(max_tmp, nums[i]);}--i;sum = 0;}}return max_tmp;}
};
官方思路一:动态规划
- 思路:类似于滚动数组的思想。若使用 p r e ( i ) pre(i) pre(i) 表示以下标 i i i 为结尾的“连续子数组最大和”,显然我们只需要滚动遍历寻找 max 0 ≤ i ≤ n − 1 { p r e ( i ) } \max_{0 \le i \le n-1}\{ pre(i)\} max0≤i≤n−1{pre(i)} 即可。那每一步如何计算 p r e ( i ) pre(i) pre(i) 呢?可以使用递推的思想,也就是: p r e ( i ) = max { p r e ( i − 1 ) + nums [ i ] , nums [ i ] } 且 p r e ( 0 ) = nums [ 0 ] pre(i) = \max \{ pre(i-1) + \textit{nums}[i], \textit{nums}[i] \} \; 且 \; pre(0) = \textit{nums}[0] pre(i)=max{pre(i−1)+nums[i],nums[i]}且pre(0)=nums[0]。
- 时间复杂度: O ( n ) O(n) O(n),其中 n n n 为 nums \textit{nums} nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
- 空间复杂度: O ( 1 ) O(1) O(1)。我们只需要常数空间存放若干变量。
- 时间80ms(92.74%),内存64.91MB(55.59%)。
class Solution {
public:int maxSubArray(vector<int>& nums) {int pre = 0, maxAns = nums[0];for (const auto &x: nums) {pre = max(pre + x, x); // 求解本步骤的pre(i)maxAns = max(maxAns, pre); // 求解最大值}return maxAns;}
};
官方思路二:分治
- 思路:我们想通过定义一个递归函数
get(nums,l,r)表示查询nums序列[l,r]区间 的最大子段和,于是get(nums,0,nums.size()-1)就可以直接完成题目。每次查询时,都将区间拆成左右两个子区间 [ l , m ] [l,m] [l,m]、 [ m + 1 , r ] [m+1,r] [m+1,r]( m = ⌊ l + r 2 ⌋ m = \lfloor \frac{l + r}{2} \rfloor m=⌊2l+r⌋),直到子区间长度为1,然后再逐级根据两个子区间的信息返回当前子区间的信息。每个区间的“信息”包括四个:
- lSum \textit{lSum} lSum 表示 [ l , r ] [l,r] [l,r] 内以 l l l 为左端点的最大子段和
- rSum \textit{rSum} rSum 表示 [ l , r ] [l,r] [l,r] 内以 r r r 为右端点的最大子段和
- mSum \textit{mSum} mSum 表示 [ l , r ] [l,r] [l,r] 内的最大子段和
- iSum \textit{iSum} iSum 表示 [ l , r ] [l,r] [l,r] 的区间和
显然区间长度为1时,四个量都等于序列值。区间长度大于1时:
- 首先最好维护的是 iSum \textit{iSum} iSum,区间 [ l , r ] [l,r] [l,r] 的 iSum \textit{iSum} iSum 就等于「左子区间」的 iSum \textit{iSum} iSum 加上「右子区间」的 iSum \textit{iSum} iSum。
- 对于 [ l , r ] [l,r] [l,r] 的 lSum \textit{lSum} lSum,存在两种可能,它要么等于「左子区间」的 lSum \textit{lSum} lSum,要么等于「左子区间」的 iSum \textit{iSum} iSum 加上「右子区间」的 lSum \textit{lSum} lSum,二者取大。
- 对于 [ l , r ] [l,r] [l,r] 的 rSum \textit{rSum} rSum,同理,它要么等于「右子区间」的 rSum \textit{rSum} rSum,要么等于「右子区间」的 iSum \textit{iSum} iSum 加上「左子区间」的 rSum \textit{rSum} rSum,二者取大。
- 当计算好上面的三个量之后,就很好计算 [ l , r ] [l,r] [l,r] 的 mSum \textit{mSum} mSum 了。我们可以考虑 [ l , r ] [l,r] [l,r] 的 mSum \textit{mSum} mSum 对应的区间是否跨越 m m m——它可能不跨越 m m m,也就是说 [ l , r ] [l,r] [l,r] 的 mSum \textit{mSum} mSum 可能是「左子区间」的 mSum \textit{mSum} mSum 和 「右子区间」的 mSum \textit{mSum} mSum 中的一个;它也可能跨越 m m m,可能是「左子区间」的 rSum \textit{rSum} rSum 和 「右子区间」的 lSum \textit{lSum} lSum 求和。三者取大。
- 时间92ms(63.50%),内存64.87MB(59.37%)。
力扣官方 注:这个分治方法类似于「线段树求解最长公共上升子序列问题」的
pushUp操作。 也许读者还没有接触过线段树,没有关系,方法二的内容假设你没有任何线段树的基础。当然,如果读者有兴趣的话,推荐阅读线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」,还是非常有趣的。
class Solution {
public:// 每个区间[l,r]都定义了四种量struct Status {int lSum, // 区间[l,r]内,以 l 为左端点的最大子段和rSum, // 区间[l,r]内,以 r 为右端点的最大子段和mSum, // 区间[l,r]内的最大子段和iSum; // 区间[l,r]的区间和};// 根据左右子区间的信息,计算当前区间的信息Status pushUp(Status l, Status r) {int iSum = l.iSum + r.iSum;int lSum = std::max(l.lSum, l.iSum + r.lSum);int rSum = std::max(r.rSum, r.iSum + l.rSum);int mSum = std::max(std::max(l.mSum, r.mSum), l.rSum + r.lSum);return Status { lSum, rSum, mSum, iSum };};// 分治法:采用递归思想Status get(std::vector<int>& a, int l, int r) {// 长度为1,直接返回if (l == r) {return Status { a[l], a[l], a[l], a[l] };}// 将区间对半分,递归寻找每个子区间的信息int m = (l + r) >> 1; // 区间的中点Status lSub = get(a, l, m); // 左子区间Status rSub = get(a, m + 1, r); // 右子区间return pushUp(lSub, rSub); // 根据左右子区间信息,计算当前区间最大字段和}// 主函数int maxSubArray(std::vector<int>& nums) {return get(nums, 0, nums.size() - 1).mSum;}
};
14. 中等-合并区间
15. 中等-轮转数组
16. 中等-除自身以外数组的乘积
17. 困难-缺失的第一个正数
矩阵
18. 中等-矩阵置零
19. 中等-螺旋矩阵
20. 中等-旋转图像
21. 中等-搜索二维矩阵II
我的思路
思路:
时间??ms(??%),内存??MB(??%)。
官方思路:
思路:
时间??ms(??%),内存??MB(??%)。
相关文章:

13-21-普通数组、矩阵
LeetCode 热题 100 文章目录 LeetCode 热题 100普通数组13. 中等-最大子数组和14. 中等-合并区间15. 中等-轮转数组16. 中等-除自身以外数组的乘积17. 困难-缺失的第一个正数 矩阵18. 中等-矩阵置零19. 中等-螺旋矩阵20. 中等-旋转图像21. 中等-搜索二维矩阵II 本文存储我刷题的…...
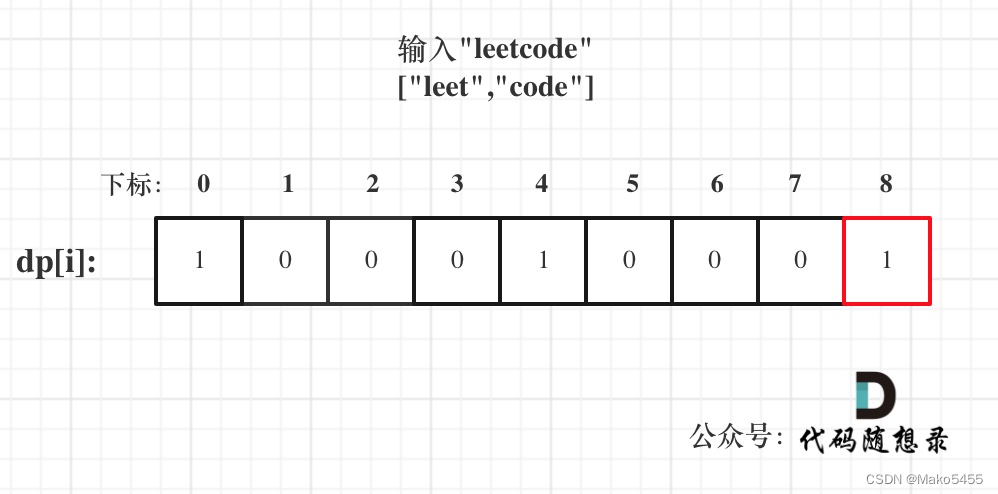
代码随想录算法训练营第四十六天【动态规划part08】 | 139.单词拆分、背包总结
139.单词拆分 题目链接: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 求解思路: 单词是物品,字符串s是背包,单词能否组成字符串s,就是问物品能不能把背包装满。 动规五部曲 确定dp数…...

go语言基础 break和contine区别
背景 break和continue是编程语言的标准语法,几乎在所有的语言都有类似的用法。 go语言及所有其他编程语言for循环或者其他循环 区别 for i : 0; i < 10; i {if i 5 {continue}fmt.Println(i)for j : 0; j < 3; j {fmt.Println(strconv.Itoa(j) "a&q…...
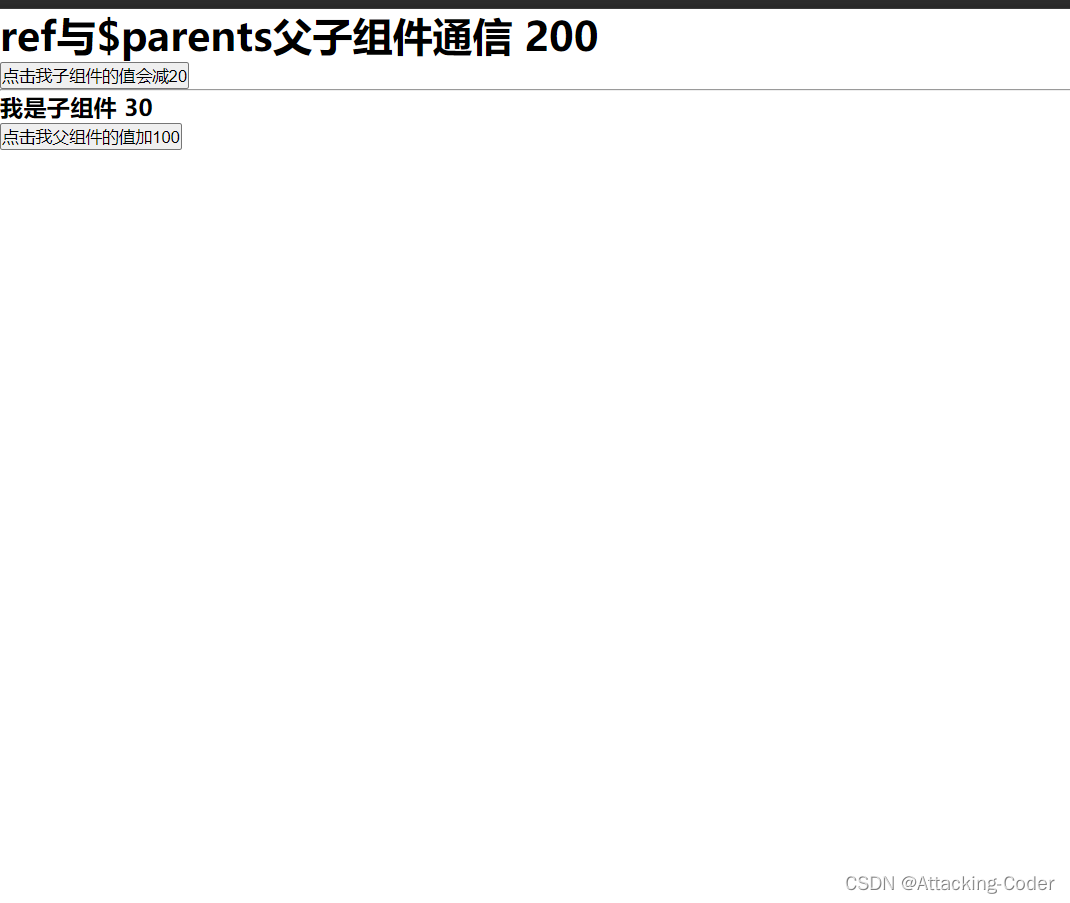
vue3父子组件通过$parent与ref通信
父组件 <template><div><h1>ref与$parents父子组件通信 {{ parentMoney }}</h1><button click"handler">点击我子组件的值会减20</button><hr><child ref"children"></child></div> </te…...

PHP中的常见的超全局变量
PHP是一种广泛使用的服务器端脚本语言,它被用于开发各种Web应用程序。在PHP中,有一些特殊的全局变量,被称为超全局变量。超全局变量在整个脚本中都是可用的,无需使用global关键字来访问它们。在本文中,我们将深入了解P…...
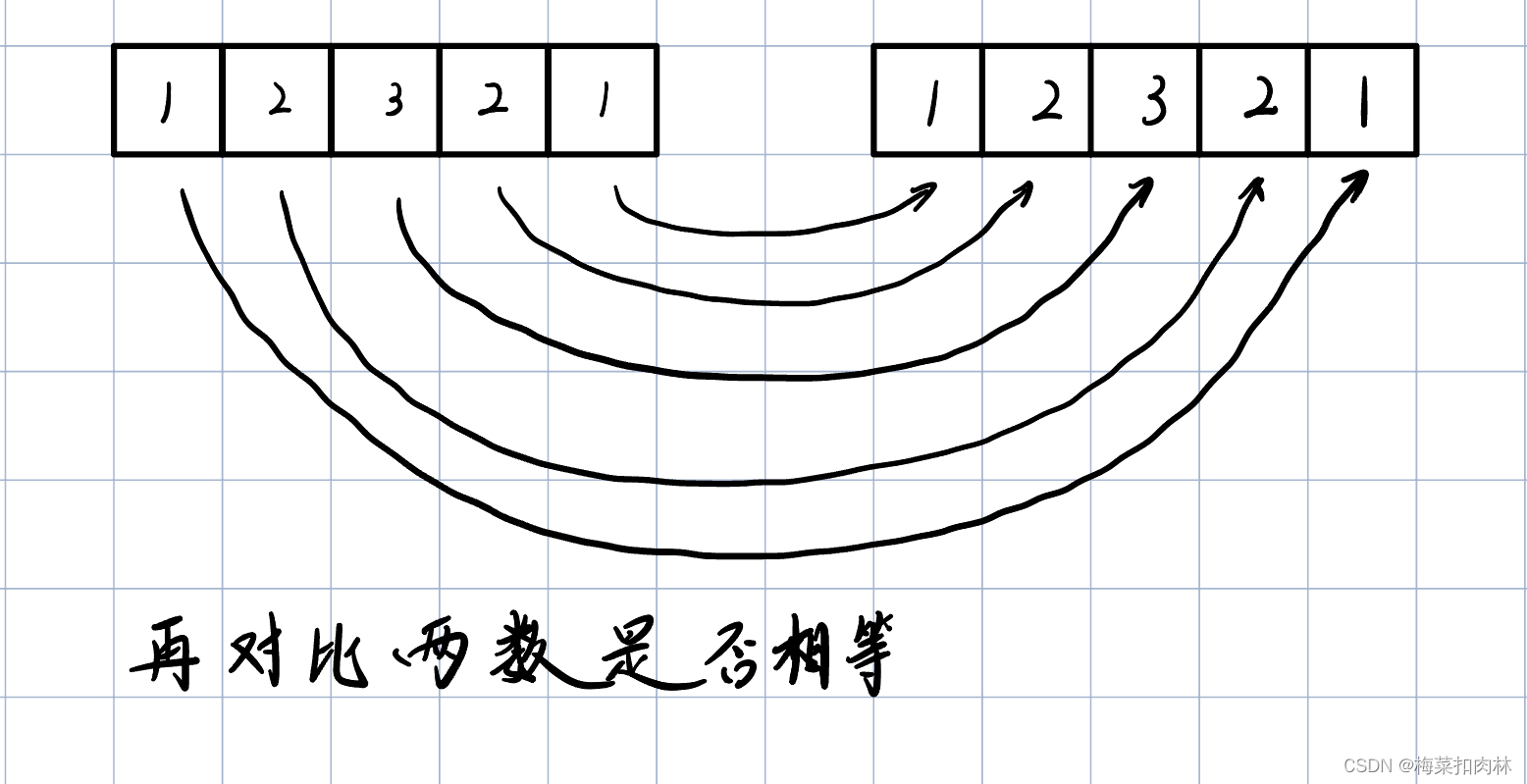
leetcode9.回文数
回文数 0.题目1.WJQ的思路2.实现过程2.0 原始值怎么一个个取出来?2.1 取出来的数如何存到新的数字后面?2.2完整的反转得到新数的过程 3.完整的代码4.可运行的代码5.算法还可以优化的部分 0.题目 给你一个整数 x ,如果 x 是一个回文整数&…...
)
springboot(ssm大学生二手电子产品交易平台 跳蚤市场系统Java(codeLW)
springboot(ssm大学生二手电子产品交易平台 跳蚤市场系统Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或…...
关于微信小程序中如何实现数据可视化-echarts动态渲染
移动端设备中,难免会涉及到数据的可视化展示、数据统计等等,本篇主要讲解原生微信小程序中嵌入echarts并进行动态渲染,实现数据可视化功能。 基础使用 首先在GitHub上下载echarts包 地址:https://github.com/ecomfe/echarts-for…...

在Windows WSL (Linux的Windows子系统)上运行的Ubuntu如何更改主机名
在Windows 安装的Ubuntu,如何修改主机名。有列了两种方法,提供给大家参照。 文章目录 方法一:hostname指令修改方法二:修改配置文件修改hostnanmewsl.conf 文件配置选项推荐阅读 方法一:hostname指令修改 hostname指…...

如何使用内网穿透将Tomcat网页发布到公共互联网上【内网穿透】
文章目录 前言1.本地Tomcat网页搭建1.1 Tomcat安装1.2 配置环境变量1.3 环境配置1.4 Tomcat运行测试1.5 Cpolar安装和注册 2.本地网页发布2.1.Cpolar云端设置2.2 Cpolar本地设置 3.公网访问测试4.结语 前言 Tomcat作为一个轻量级的服务器,不仅名字很有趣࿰…...
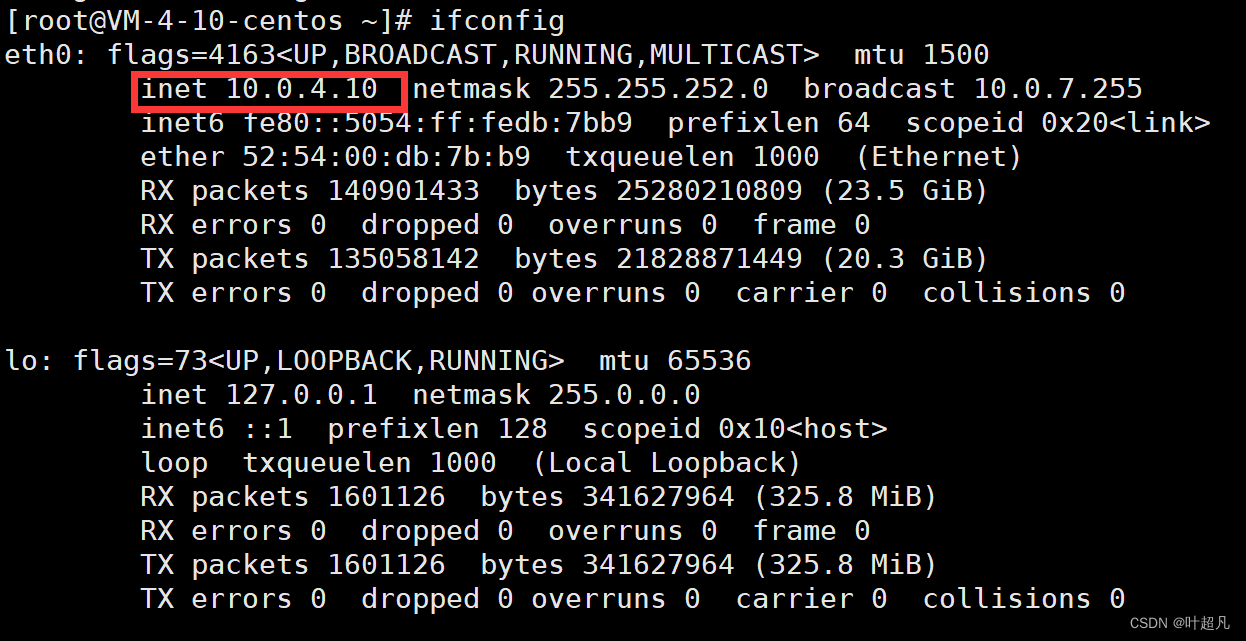
网络入门---网络的大致了解
目录标题 网络发展的简单认识协议作用的理解协议的本质什么是协议分层网络通信所面对的问题OSI七层模型TCP/IP模型协议报头的理解局域网通信局域网通信基本原理报头的问题局域网的特点跨网的网络链接如何查看mac地址 网络发展的简单认识 通过之前的学习我们知道计算机是给人提…...
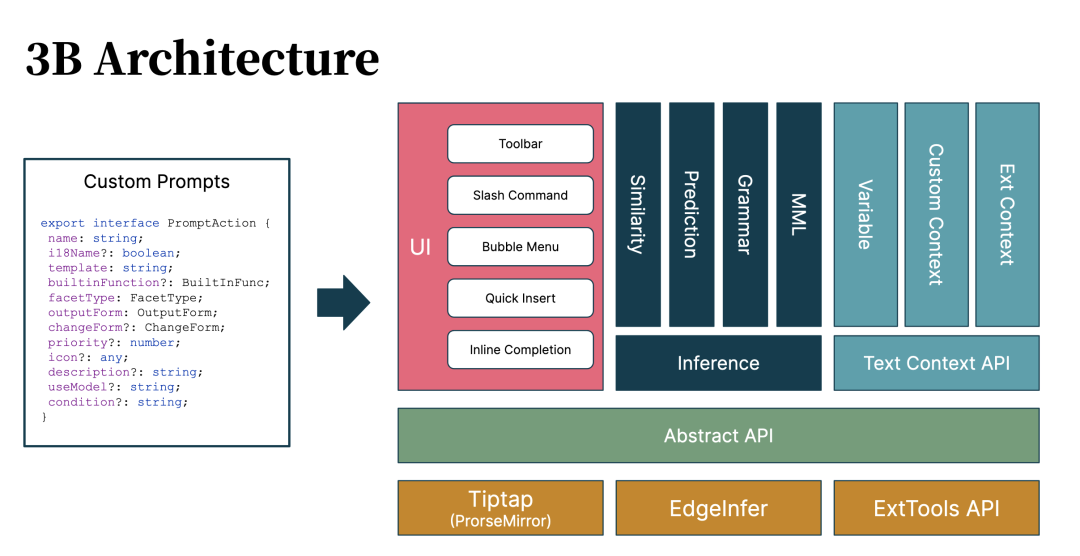
构建沉浸式 AI 文本编辑器:开源 3B 编辑器的设计原则与思路
借助于在 AutoDev 与 IDE 上的 AI 沉浸式体验设计,我们开始构建一个 AI 原生的文本编辑器,以探索沉浸式创作体验。其适用于需求编写、架构文档等等文档场景,以加速软件开发中的多种角色的日常工作。 GitHub:https://github.com/un…...
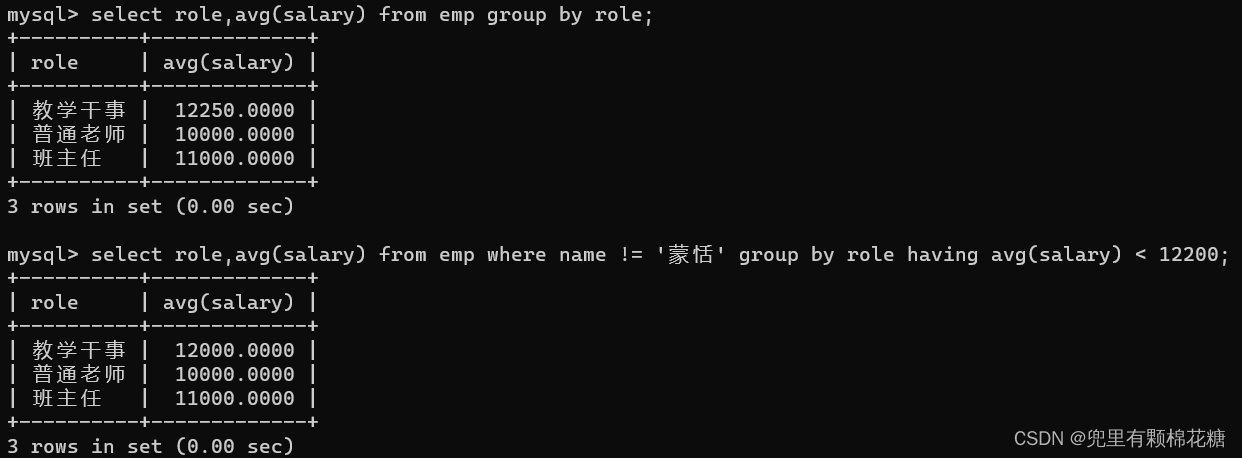
【从删库到跑路 | MySQL总结篇】表的增删查改(进阶上)
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【MySQL学习专栏】🎈 本专栏旨在分享学习MySQL的一点学习心得,欢迎大家在评论区讨论💌 目录 一、数据…...
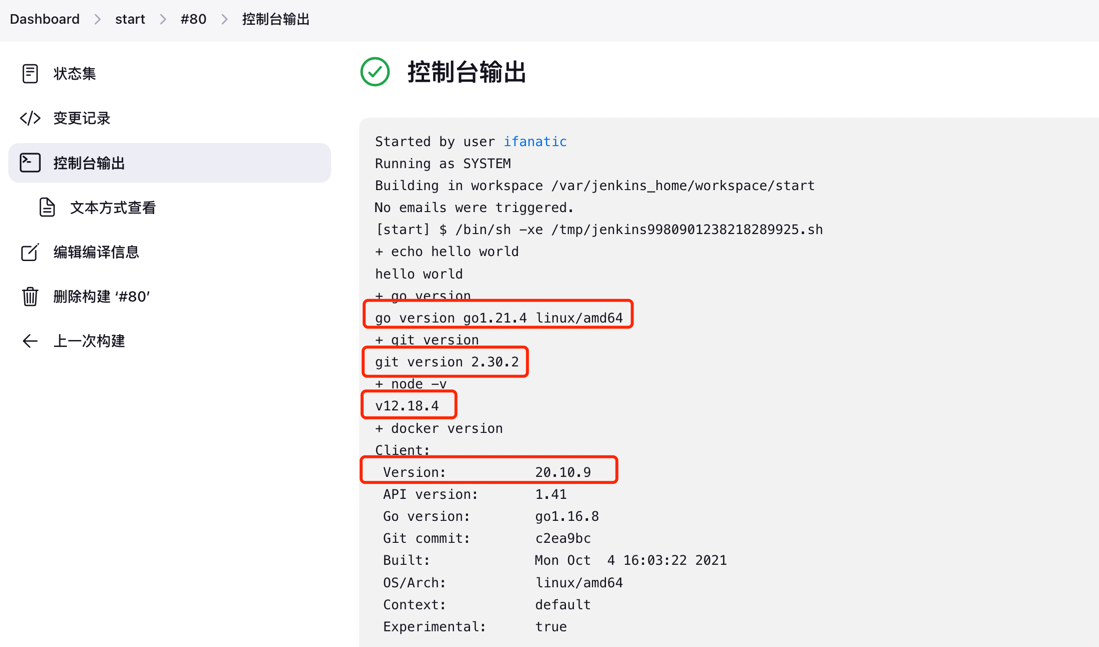
[每周一更]-(第74期):Docker-compose 部署Jenkins容器-英文版及错误纠错
1、前文概要 通过物理机部署Jenkins前文已经讲过(地址:[Jenkins] 物理机 安装 Jenkins),也已经公司内部平稳运行若干年,考虑到容器化的使用场景,部分项目都采用容器运行,开始考虑部署容器化的J…...
MySQL日期函数sysdate()与now()的区别,获取当前时间,日期相关函数
select sleep(2) as datetime union all select sysdate() -- sysdate() 返回的时间是当前的系统时间,而 now() 返回的是当前的会话时间。 union all select now() -- 等价于 localtime,localtime(),localtimestamp,localtimestamp(),current_timestamp,curre…...

邦芒解析:面试怎么谈自身优缺点
在面试时,当被问到你的优缺点时,你可以这样回答: 优点: 我的工作能力强,能够高效地完成任务。我对技术有热情,喜欢学习新的技能和知识。我善于沟通,能够与不同背景的人进行有效沟通。我注重细节…...

【libGDX】加载G3DJ模型
1 前言 libGDX 提供了自己的 3D 格式模型文件,称为 G3D,包含 g3dj(Json 格式)和 g3db(Binary 格式)文件,官方介绍见 → importing-blender-models-in-libgdx。 对于 fbx 文件,libGDX…...

0基础学习VR全景平台篇第123篇:VR视频航拍补天 - PR软件教程
上课!全体起立~ 大家好,欢迎观看蛙色官方系列全景摄影课程! 嗨,大家好,今天我们来介绍【航拍VR视频补天】。之前已经教给了大家如何处理航拍图片的补天,肯定有很多小伙伴也在好奇,航拍的VR视频…...

webpack打包三方库直接在html里面使用
场景:我是小程序中使用wxmp-rsa库进行加密,然后在html里面解密 我就想把wxmp-rsa库打包到一个js里面,然后在html里面直接引入使用。 webpack配置 const path require("path"); const MiniCssExtractPlugin require("mini-…...

Redis使用increment方法返回null的原因以及解决方案
public static void main(String[] args) {redisTemplate.setEnableTransactionSupport(true); //开启事务支持redisTemplate.multi(); //标记事务块的开始redisTemplate.opsForValue().set("name","zs");redisTemplate.opsForValue().set("pass&qu…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
