【数据结构】什么是栈?
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌栈的定义
📌元素进栈出栈的顺序
📌栈的抽象数据类型
📌栈的顺序存储结构
📌栈的链式存储结构
链栈的进栈操作
链栈的出栈操作
📌栈的应用
🎏递归
🎏括号匹配问题
🎏四则运算表达式求值
结语
人生,需要有进栈出栈精神的体现.在哪里跌倒,就应该在哪里爬起来.无论陷入何等困境,只要抬头能仰望蓝天,就有希望,不断进取,你就可以让出头之日重现.困难不会永远存在,强者才能勇往直前. ——封清扬
📌栈的定义
栈和队列是两种重要的线性结构.从数据结构角度看,栈和队列也是线性表,其特殊性在于栈和队列的基本操作是线性表操作的子集,它们是操作受限的线性表,因此,可称为限定性的数据结构.但从数据类型角度看,它们是和线性表大不相同的两类重要的抽象数据类型.
栈(stack)是限定仅在表尾进行插入和删除操作的线性表.
我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈.栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构.
要理解栈这个概念,我们需要注意,首先栈是一个线性表,也就是说,栈具有线性关系,即前驱后继关系.只不过它是一种特殊的线性表而已.定义中说栈在线性表的尾部进行插入和删除操作,这里的表尾指的是栈顶,而不是栈底.
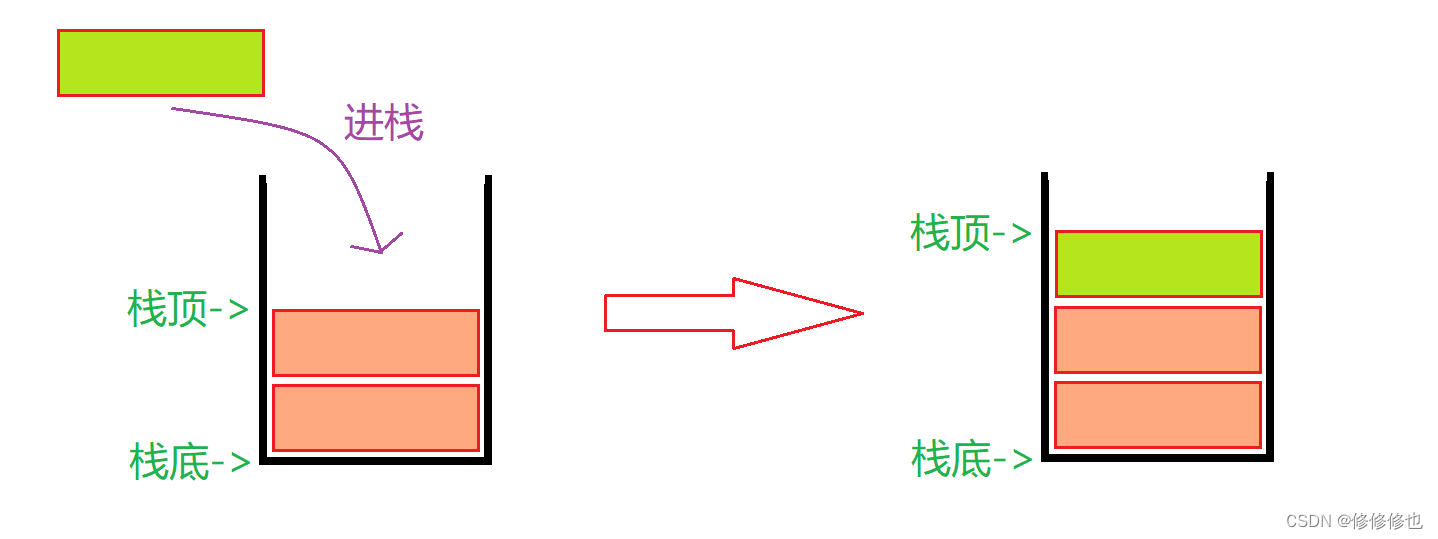
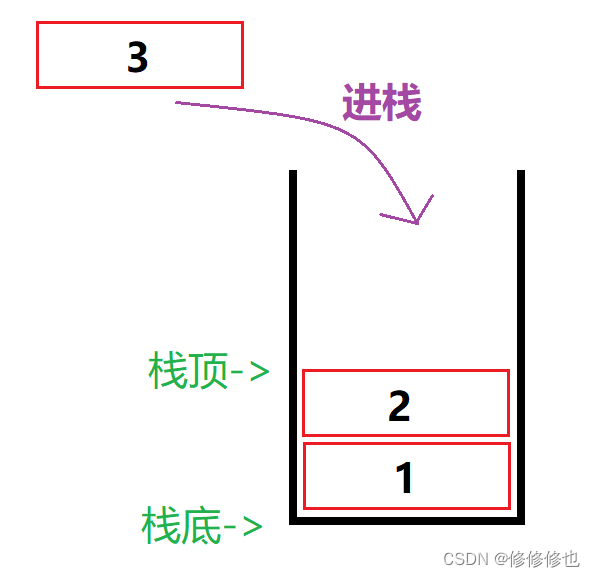
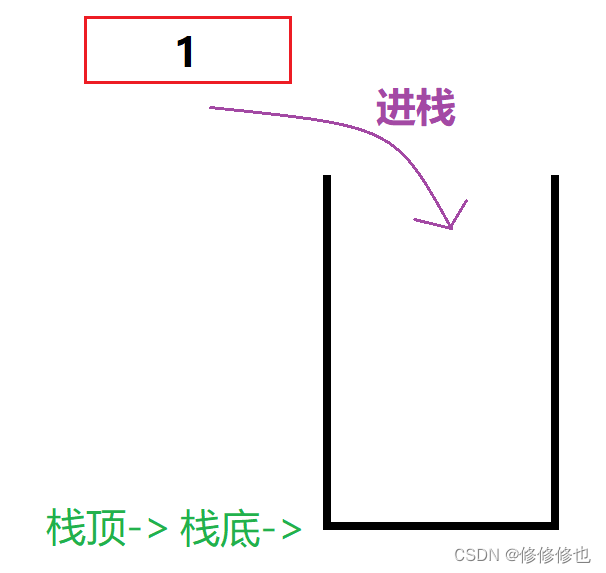
栈的插入操作,叫做进栈,也称压栈,入栈.类似于子弹入弹夹,如下图:
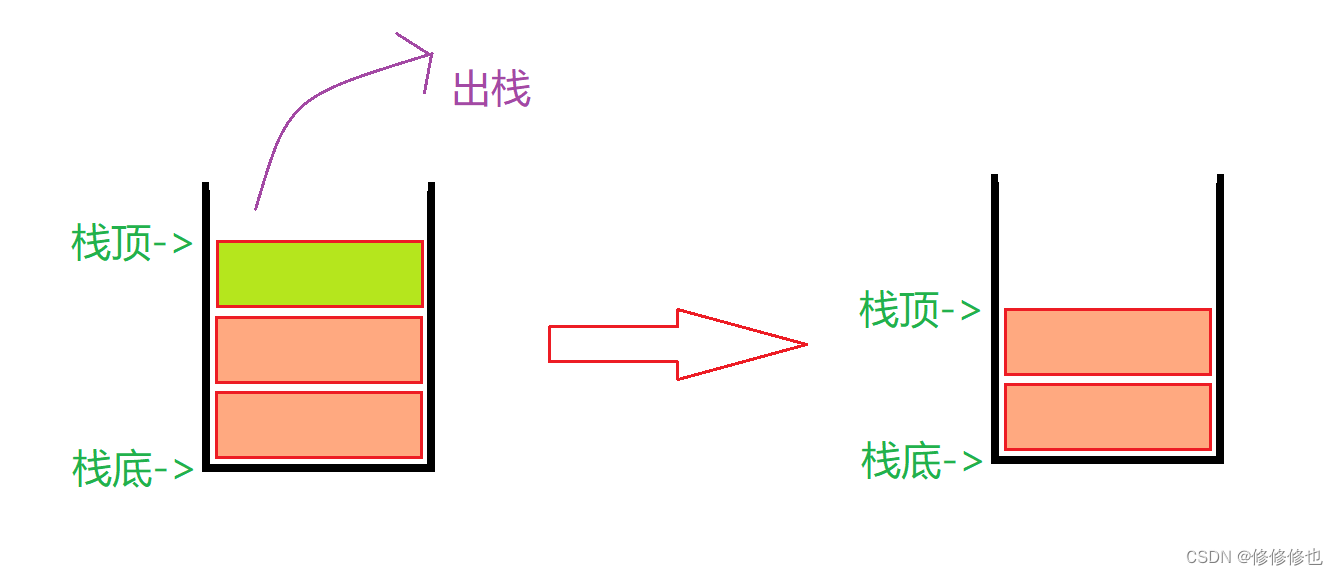
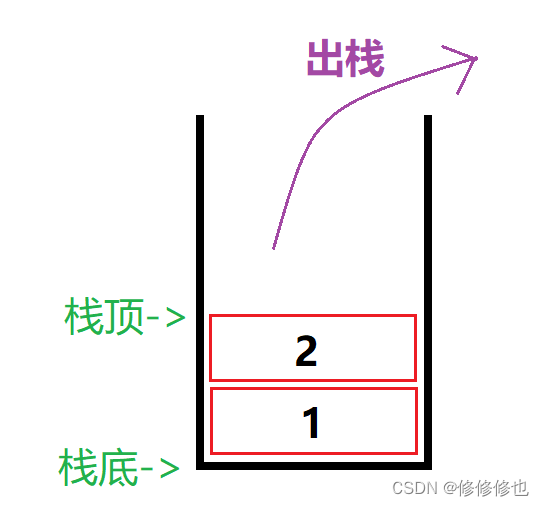
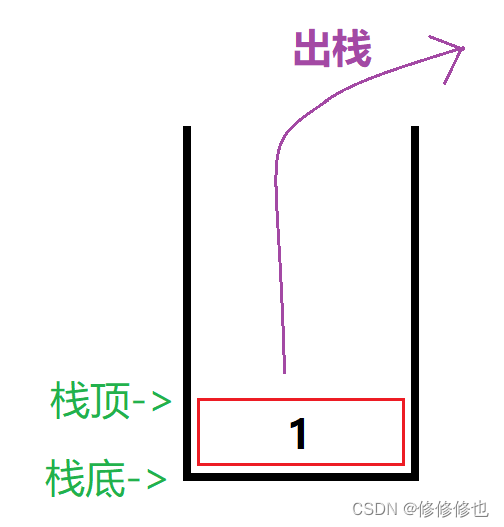
栈的删除操作,叫作出栈,也有的叫作弹栈.如同弹夹中的子弹出弹夹,如下图:
生活中类似于栈"先进后出"概念的东西很多,如我们平常用的抽纸,装羽毛球的球筒,装子弹的弹夹等.
📌元素进栈出栈的顺序
虽然栈的定义中规定了栈中元素必须符合先进后出的规则,但并没有对元素进出栈的时间做限制,因此最先进栈的元素,不一定就最后出栈,例如:
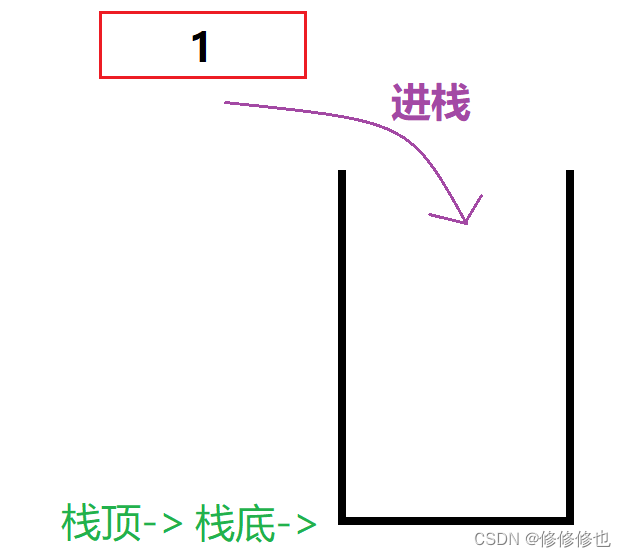
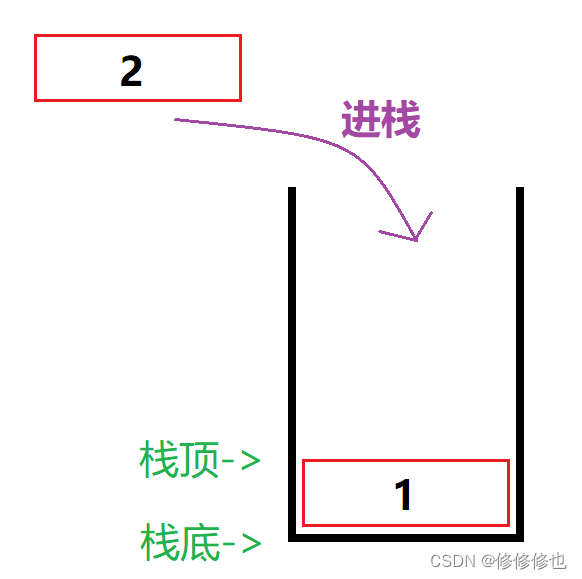
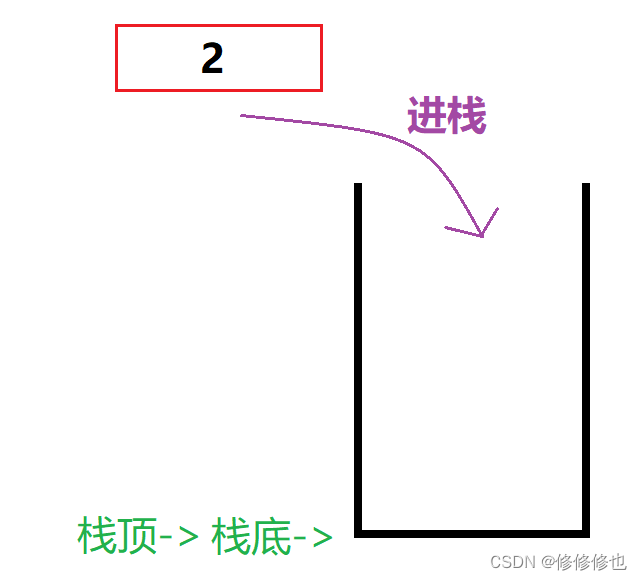
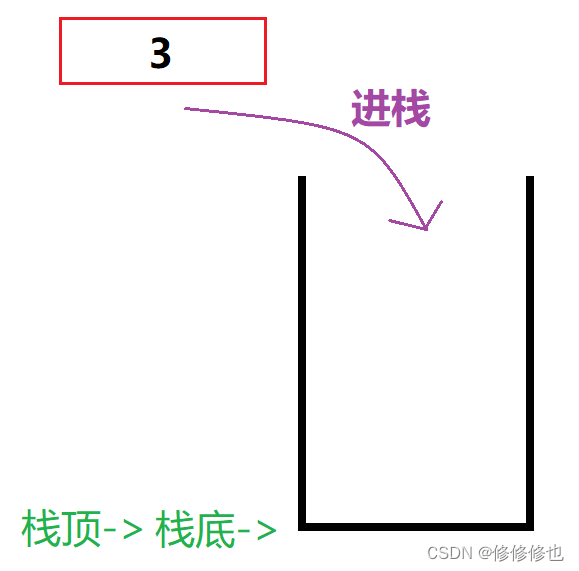
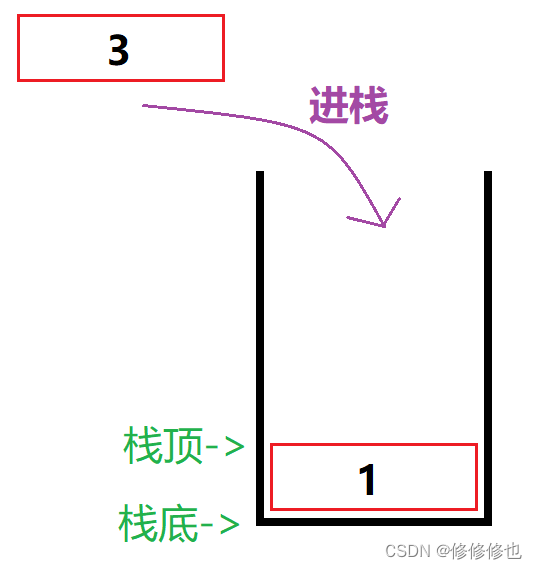
现在有三个整型元素1,2,3依次进栈,会有以下5种不同的出栈顺序:
第一种:1进,2进,3进.3出,2出,1出.
出栈顺序:321.
第二种:1进,1出,2进,2出,3进,3出.
出栈顺序:123
第三种:1进,2进,2出,1出,3进,3出.
出栈顺序:213
第四种:1进,1出,2进,3进,3出,2出.
出栈顺序:132
第五种:1进,2进,2出,3进,3出,1出,
出栈顺序:231
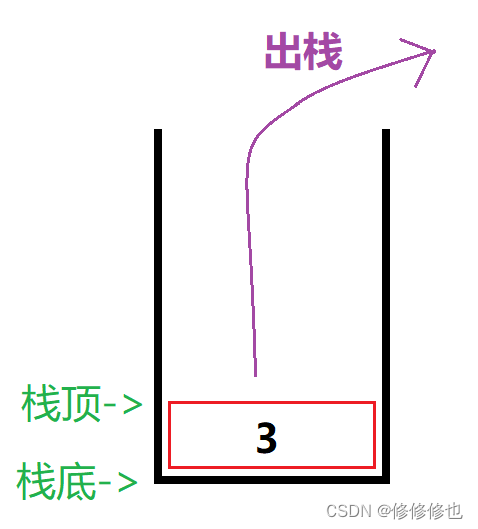
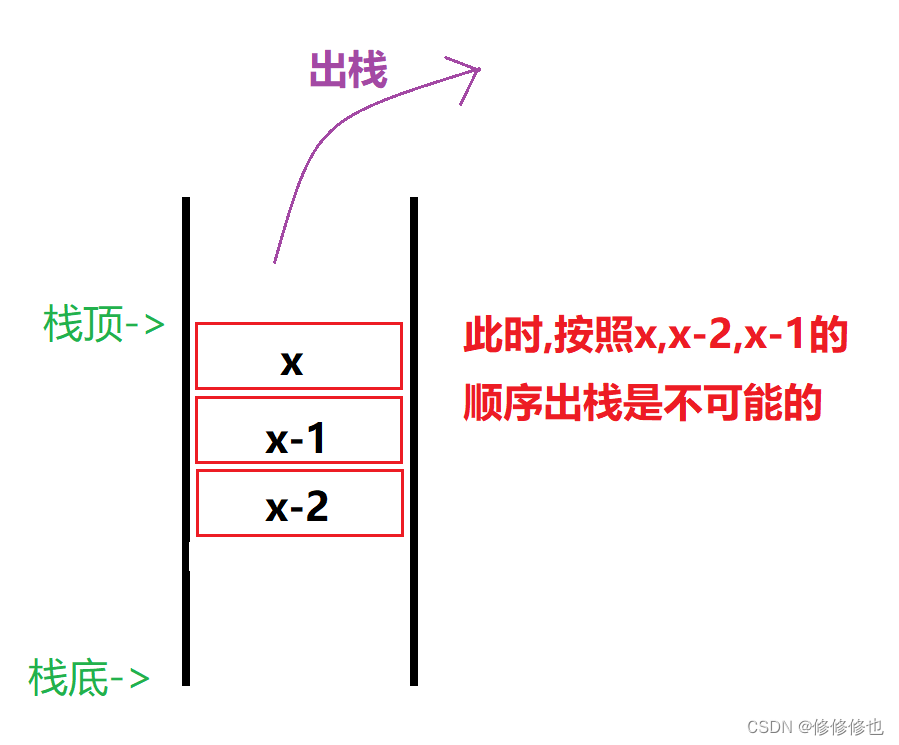
你可能会好奇,按照排列组合应该还有一个312的出栈顺序啊,为什么没写呢?别急,这是我们要重点分析的一种情况,我们把它拉出来单独分析:
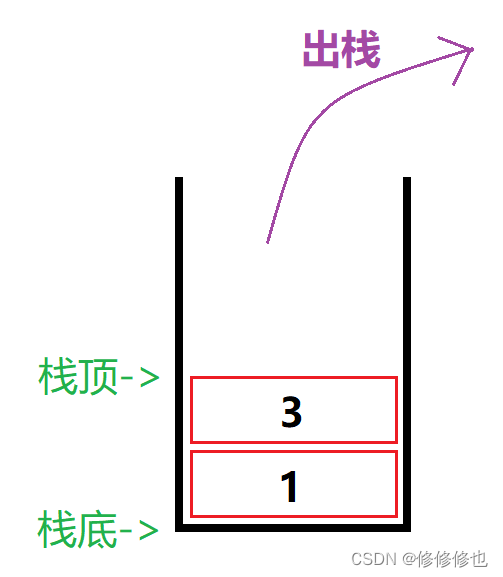
首先,要出3的话,那么3肯定进栈了.按照1,2,3的进栈顺序,3进栈了,那么1,2肯定已经进栈了,所以3出栈时栈内的情况应该是这样的:
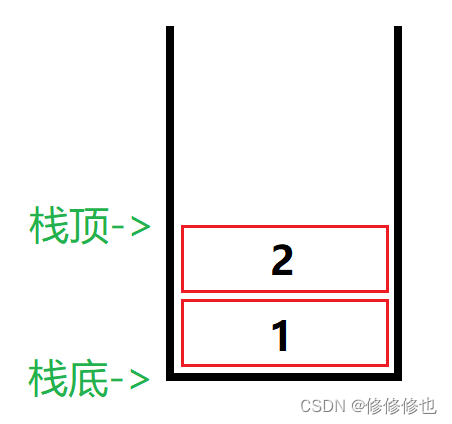
3出栈后,栈内元素情况是这样的:
可以看到,当前栈中栈顶元素为2,但我们想要出栈的元素是1,这是不可能做到的,因为按照栈的先进后出原则,我们此时只能先出2,再出1.
因此312的出栈顺序是不可能的.
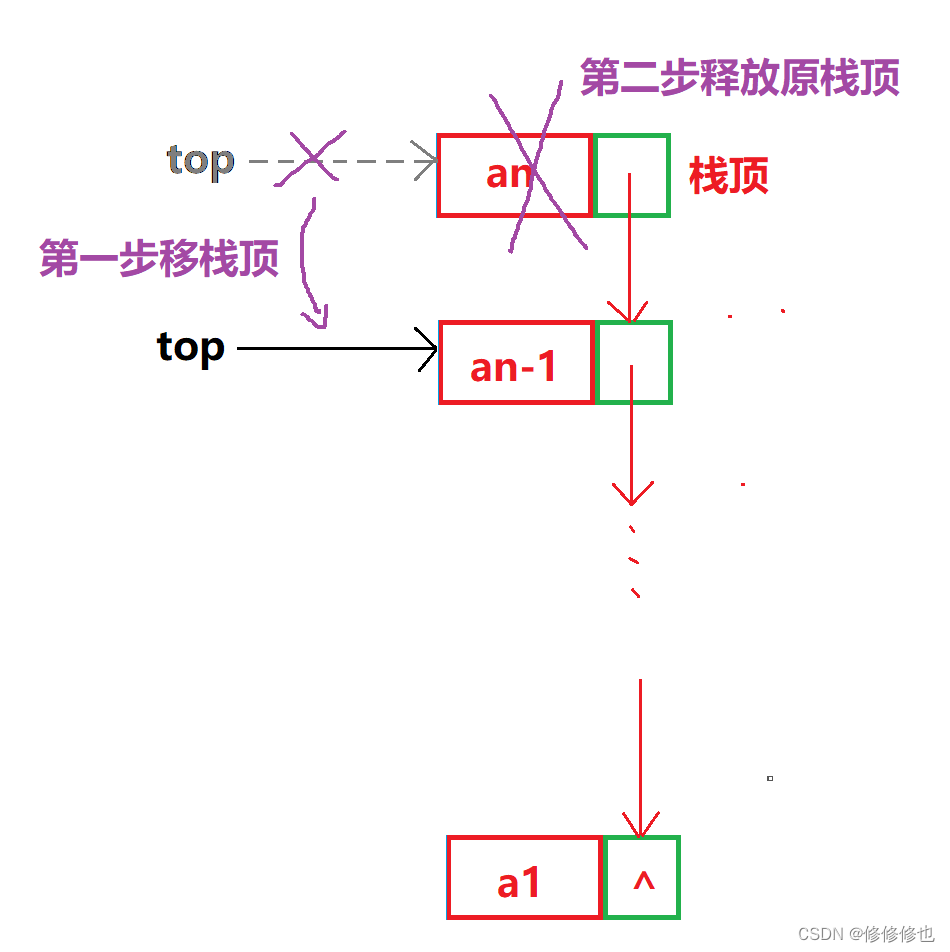
根据上述对312出栈顺序的分析,我们可以得出一个结论:
即当按照由1~x的元素顺序入栈时,假设当前栈顶元素为x,则该栈不可能实现按照x,x-2,x-1的顺序出栈.如下图:
📌栈的抽象数据类型
对于栈来讲,因为它的特殊性,因此在操作上相对于线性表有些变化,特别是插入和删除操作,只需要保留进栈和出栈两部分.
栈的抽象数据类型如下:
ADT 栈(stack)
Data栈的数据对象集合为 {a1, a2, ..., an},每个元素的类型均为STDataType.其中, 除第一个元素a1外, 每一个元素有且只有一个直接前驱元素.除了最后一个元素an外, 每一个元素有且只有一个直接后继元素.数据元素之间的关系是一对一的关系.
OperationInitStack(*s); 初始化操作, 建立一个空的栈s.DestroyStack(*s) 若栈存在,则销毁它.StackEmpty(s); 若栈为空,返回true,否则返回false.ClearStack(*s); 将栈清空.GetTop(s, *e); 若栈存在且非空,用e返回s的栈顶元素.Push(*s,e); 若栈s存在,插入新元素e到栈s中并成为栈顶元素.Pop(*s,*e); 删除栈s中栈顶元素,并用e返回其值.StackLength(s); 返回栈s的元素个数.
endADT📌栈的顺序存储结构
顺序栈和顺序表一样,都是使用数组来实现的,对于栈这种只能一头插入和删除的线性表来说,使用下标为0的一端做为栈底比较好.因为顺序表尾插和尾删的时间复杂度都是O(1),而头插和头删因为要挪动元素,所以时间复杂度为O(n).对比来看,显然是用下标为0的一端做头,然后在数组尾部进栈出栈是较优的选择.
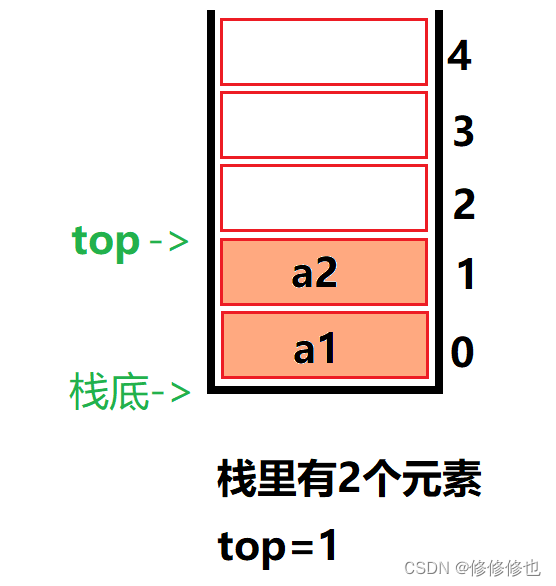
在顺序栈中需要包含三个要素:存储数据的数组arr,顺序栈的当前存储容量capacity,顺序栈栈顶元素的位置top.
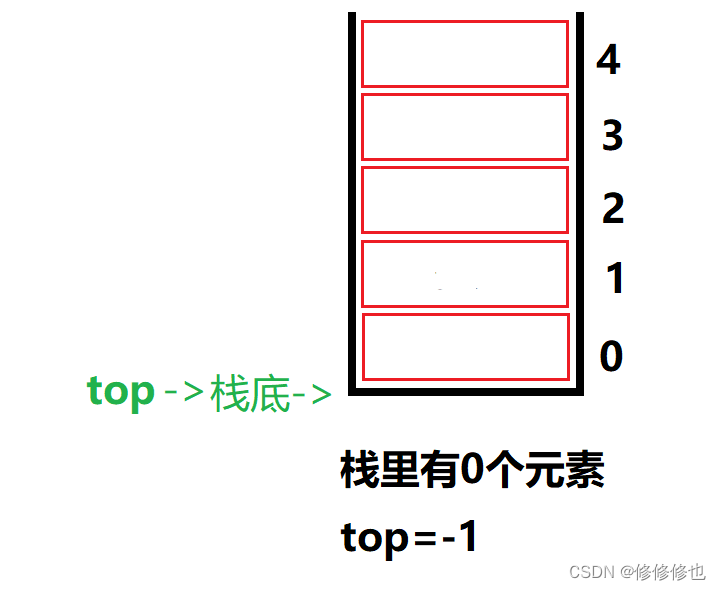
随着数据的进栈和出栈,top的位置是在变化的,但无论如何top也不能够比数组容量capacity还要大.因此top必须小于capacity.当栈中存在一个元素时,top=0,因此同常把空栈的判定条件设为top=-1.
若现在有一个顺序栈,capacity是5,则栈普通情况,空栈和满栈的情况示意图如下:
在顺序栈中,进栈和出栈的逻辑完全和顺序表的尾插尾删逻辑一样,后续我们会一起实现一个顺序栈的程序,因此在这里就不多赘述了.
📌栈的链式存储结构
栈的链式存储结构,简称为链栈.
因为栈只在栈顶插入或删除的特性,我们在设计链栈时应当把栈顶放在单链表的头部,并且对链表来说,头指针是必须的,而对链栈来说,栈顶指针同样是必须的,因此我们不如将他们合二为一.
链栈示意图:

对于链栈来说,基本不存在栈满的情况.而对空栈来说,链栈的判断条件应该是top=NULL.
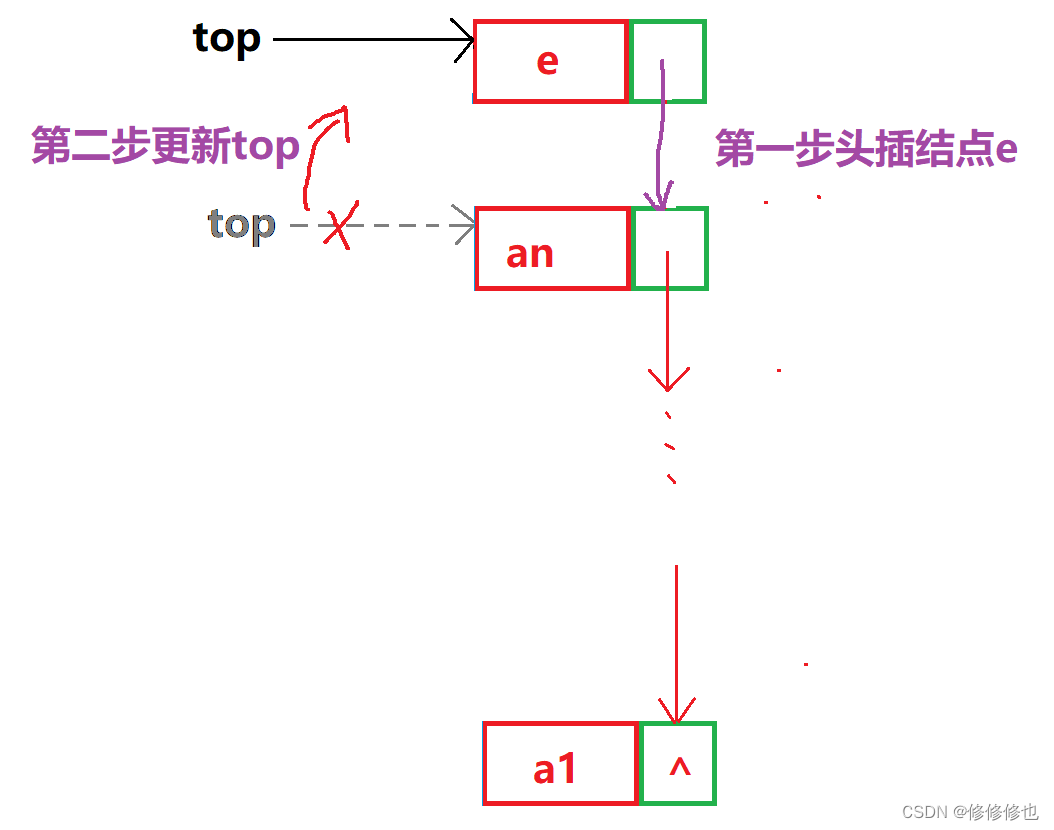
链栈的进栈操作
对于链栈的进栈push操作,假设元素新结点是e,top为栈顶指针,则进栈示意图如下:
链栈的出栈操作
对于链栈的出栈pop操作,假设top为栈顶指针,则出栈示意图如下:
📌栈的应用(待补)
🎏递归
🎏括号匹配问题
🎏四则运算表达式求值
结语
当我们了解了栈的定义后,接下来我们将一起实现一个顺序栈程序,由于篇幅有限,我会在下篇博客中为大家详细介绍一下顺序栈的实现,感兴趣的话可以点击下面链接查看:
【数据结构】用C语言实现顺序栈(附完整运行代码)![]() http://t.csdnimg.cn/ksbBH
http://t.csdnimg.cn/ksbBH
希望这篇有关数据结构栈的介绍文章能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是线性表?
【数据结构】线性表的链式存储结构
【数据结构】C语言实现顺序表万字详解(附完整运行代码)
【数据结构】C语言实现单链表万字详解(附完整运行代码)
【数据结构】C语言实现带头双向循环链表万字详解(附完整运行代码)

数据结构栈和队列篇思维导图
相关文章:

【数据结构】什么是栈?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌栈的定义 📌元素进栈出栈的顺序 📌栈的抽象数据类型 📌栈的顺序存储结构 📌栈的链式存储结构 链栈的进…...
基于C#实现鸡尾酒排序(双向冒泡排序)
通俗易懂点的话,就叫“双向冒泡排序”。 冒泡是一个单向的从小到大或者从大到小的交换排序,而鸡尾酒排序是双向的,从一端进行从小到大排序,从另一端进行从大到小排序。 从图中可以看到,第一次正向比较,我们…...
CentOS添加开机启动
1.编写项目启动脚本(run.sh) #!/bin/bash-切换到程序所在路径 cd /home/cavs_install/app/cavs-admin/target/ # 等待其他组件启动完毕后再启动本项目(如果不需要等待,本步骤可省略) sleep 300 # 实际启动命令 nohup …...
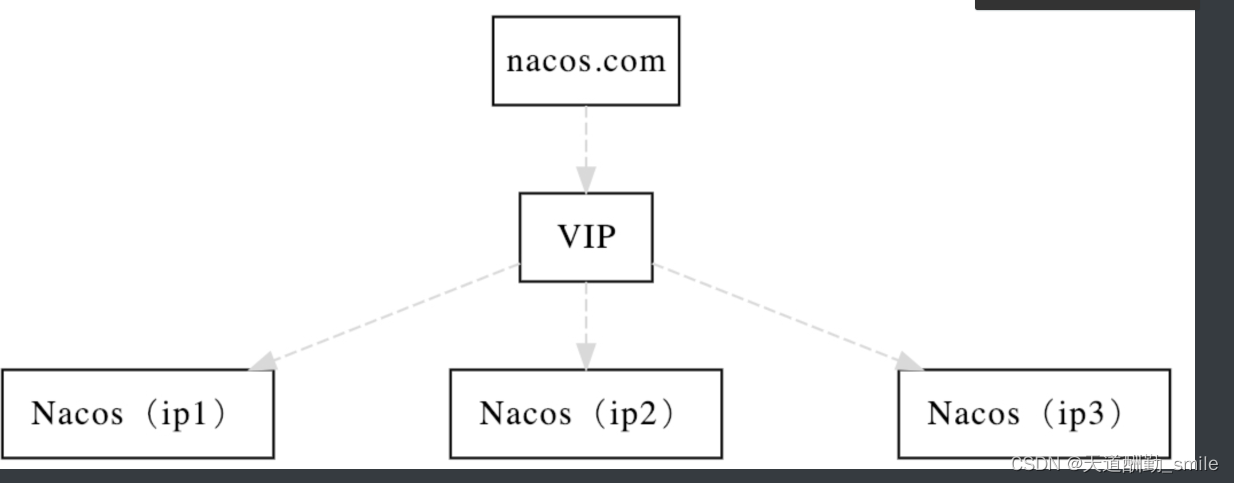
SpringCloudAlibaba之Nacos的持久化和高可用——详细讲解
目录 一、Nacos持久化 1.持久化说明 2.安装mysql数据库5.6.5以上版本(略) 3.修改配置文件 二、nacos高可用 1.集群说明 2.nacos集群架构图 2.集群搭建注意事项 3.集群规划 4.搭建nacos集群 5.安装Nginx 6.配置nginx conf配置文件 7.启动nginx进行测试即可 一、Nacos持久…...
vue3安装eslint和prettier,最简单的步骤
第1步: 安装eslint yarn add eslint -D 第2步: 在根文件夹中,创建.eslintrc.js文件 第3步: 在package.json文件中新增命令 "lint": "eslint --fix --ext .ts,.tsx,.vue src --quiet","prettier"…...

Day32| Leetcode 122. 买卖股票的最佳时机 II Leetcode 55. 跳跃游戏 Leetcode 45. 跳跃游戏 II
Leetcode 122. 买卖股票的最佳时机 II 题目链接 122 买卖股票的最佳时机 II 本题目设计的还是比较巧妙的,把最终的利润分为每天的利润就解决了(贪心),每天的利润就是前一天买进,后一天卖出,转化到代码上就…...
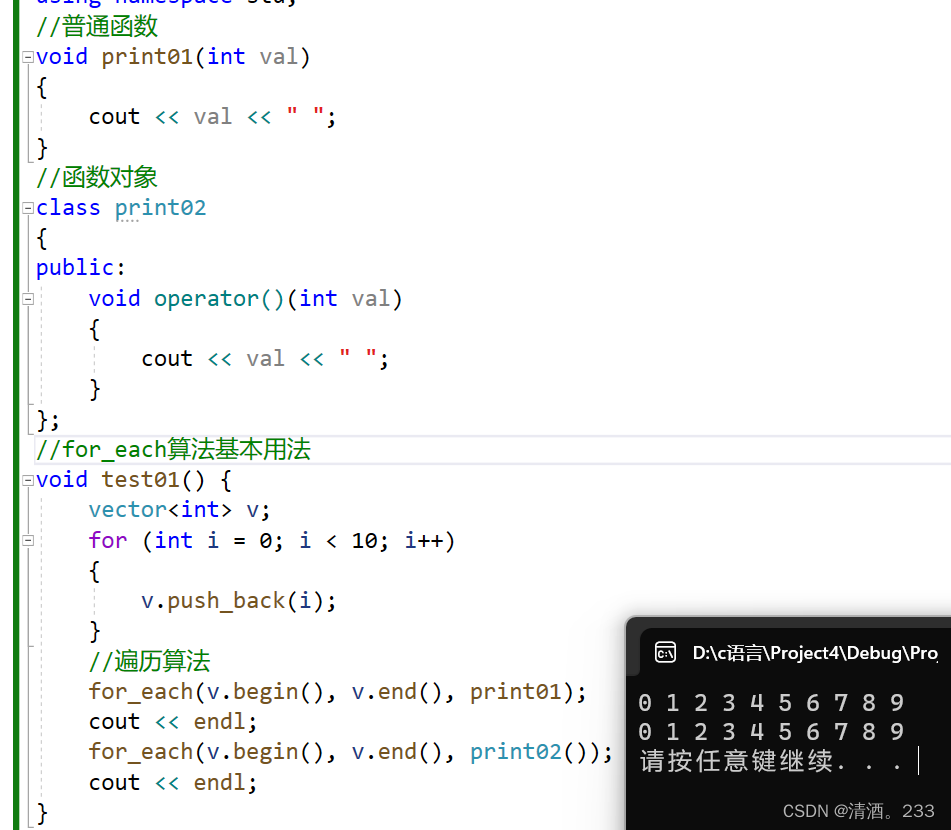
95.STL-遍历算法 for_each
算法概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。 <algorithm> 是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric> 体积很小,只包括几个在序列上面…...

Python基础语法之学习type()函数
Python基础语法之学习type函数 一、代码二、效果 查看数据类型或者说查看变量存储的数据类型 一、代码 print(type("文本")) print(type(666)) print(type(3.14))二、效果 梦想是生活的指南针,坚持追逐梦想,终将抵达成功的彼岸。不要害怕失败…...

filebeat报错dropping too large message of size
filebeat报错: dropping too large message of size 1714620. 原因: kafka对每一条消息的大小进行了限制。 解决 kafka端 修改config/server.properties,添加以下配置 max_message_bytes10000000 replica.fetch.max.bytes10000000修改…...
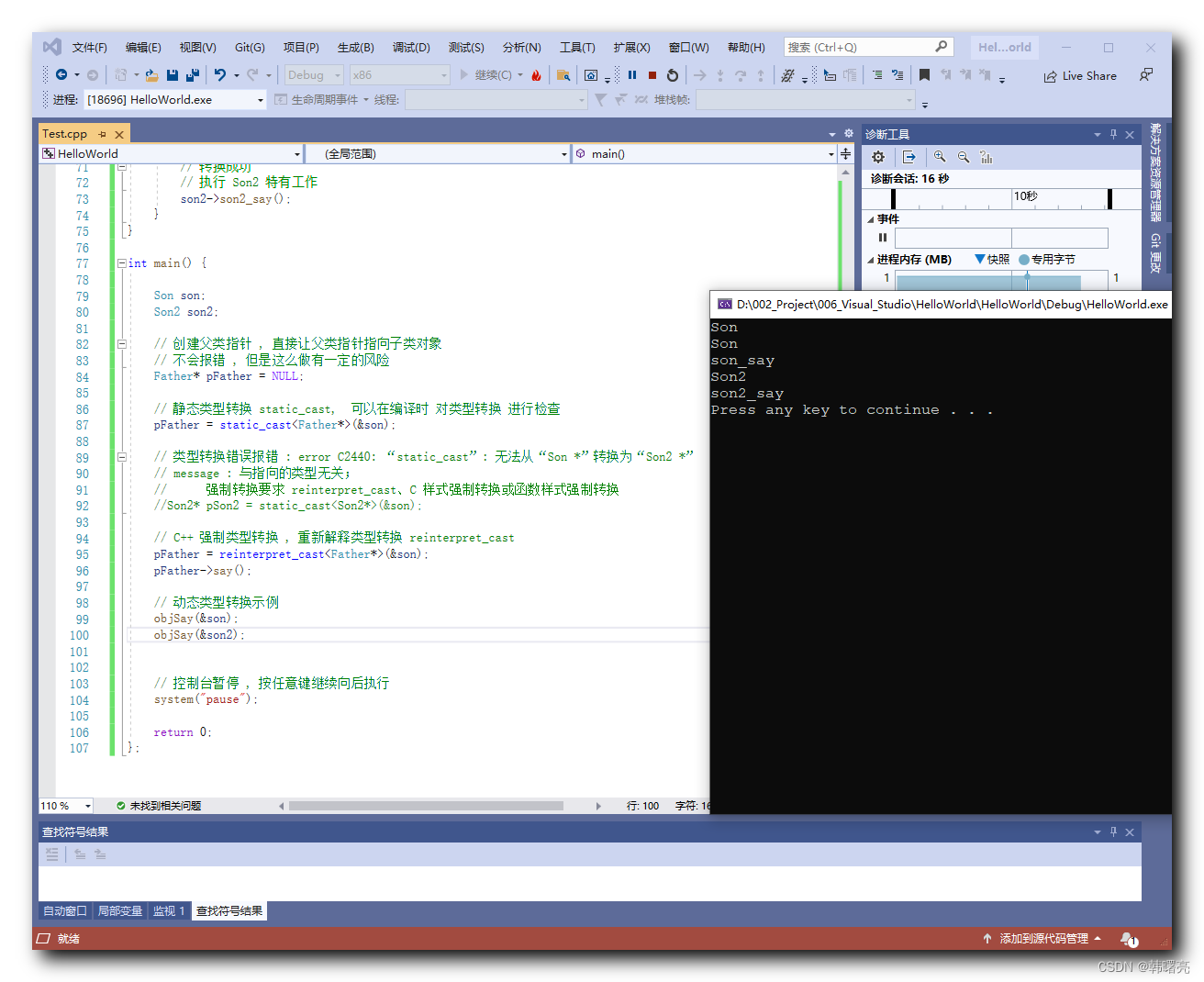
【C++】类型转换 ④ ( 子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast )
文章目录 一、子类 和 父类 之间的类型转换 - 动态类型转换 dynamic_cast1、构造父类和子类2、子类 和 父类 之间的类型转换 - 隐式类型转换3、子类 和 父类 之间的类型转换 - 静态类型转换 static_cast4、子类 和 父类 之间的类型转换 - 重新解释类型转换 reinterpret_cast5、…...

在CentOS 7.9上搭建高性能的FastDFS+Nginx文件服务器集群并实现外部远程访问
文章目录 引言第一部分:FastDFS介绍与安装1.1 FastDFS简介1.2 FastDFS安装1.2.1 安装Tracker Server1.2.2 安装Storage Server 1.3 FastDFS配置1.3.1 配置Tracker Server1.3.2 配置Storage Server1.3.3 启动FastDFS服务 第二部分:Nginx配置2.1 Nginx安装…...
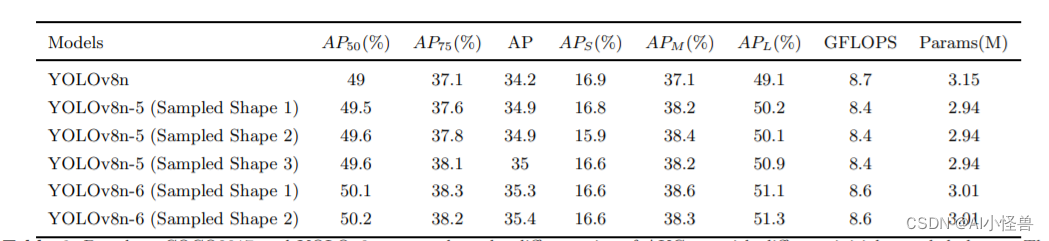
YOLOv8独家原创改进: AKConv(可改变核卷积),即插即用的卷积,效果秒杀DSConv | 2023年11月最新发表
💡💡💡本文全网首发独家改进:可改变核卷积(AKConv),赋予卷积核任意数量的参数和任意采样形状,为网络开销和性能之间的权衡提供更丰富的选择,解决具有固定样本形状和正方形的卷积核不能很好地适应不断变化的目标的问题点,效果秒殺DSConv 1)AKConv替代标准卷积进行…...

Docker pause/unpause命令
docker pause :暂停容器中所有的进程。 docker unpause :恢复容器中所有的进程。 语法 docker pause CONTAINER [CONTAINER...]docker unpause CONTAINER [CONTAINER...]实例 暂停数据库容器db01提供服务。 docker pause db01恢复数据库容器db01提供…...

PostgreSQL create or replace view和重建视图 有什么区别?
一、 replace vs 重建 遇到开发提了个问题,create or replace view和重建视图(dropcreate)有什么区别,查询资料整理了一下。 1. create or replace 当存在同名视图时,尝试将其替换新视图语句必须与现有视图查询具有相…...
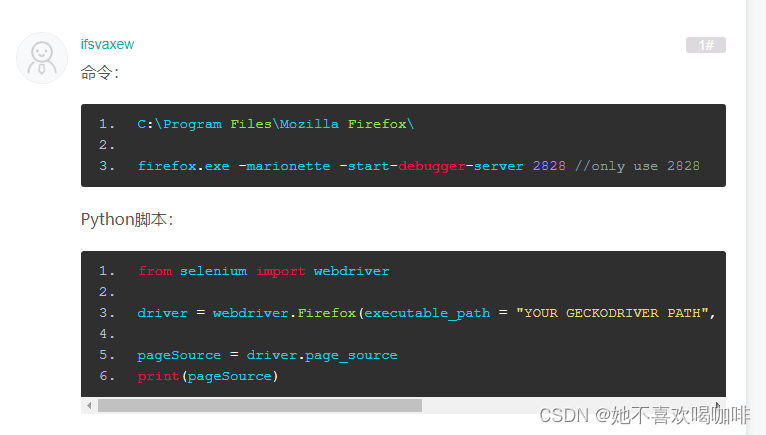
Selenium 连接到现有的 Firefox 示例
当前环境: python 3.7 selenium 3.14.1 urllib3 1.26.8 Frefox 115.1.0esr(32位) geckodriver.exe 0.33.0 1 下载 Firefox 浏览器,根据自己的需要选择。 下载 Firefox 浏览器,这里有简体中文及其他 90 多种语言版本…...
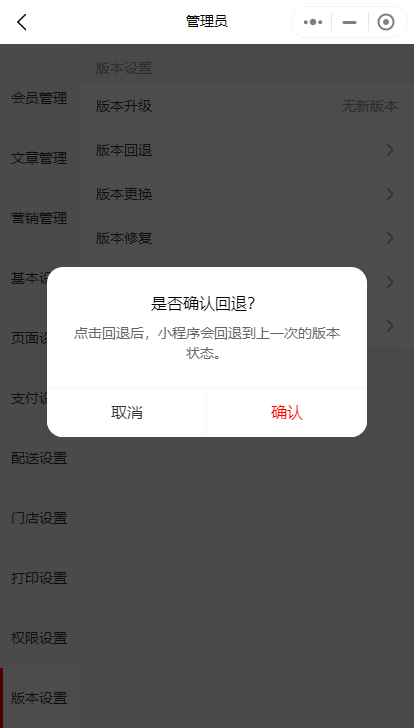
小程序如何进行版本回退
当商家决定回退小程序版本时,可能是因为新版本出现了一些问题或者不符合预期,需要恢复到之前的稳定版本。下面具体介绍怎么回退小程序的版本。 在小程序管理员后台->版本设置处,点击版本回退。确认后,小程序会回退到上一次的版…...

15:00面试,15:06就出来了,问的问题有点变态。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到8月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40%…...
)
大数据-之LibrA数据库系统告警处理(ALM-37008 MPPDB服务不可用)
告警解释 告警模块每30秒周期性检测MPPDB服务健康状态,当检测到MPPDB健康状态为“故障”时产生告警。 当检测到MPPDB健康状态为“良好”时告警恢复。 告警属性 告警ID 告警级别 可自动清除 37008 致命 是 告警参数 参数名称 参数含义 ServiceName 产生…...

Pytorch-gpu环境篇
最最最头疼的就是配环境了 包之间的版本匹配问题 INSTALLING PREVIOUS VERSIONS OF PYTORCH 要考虑到pytorch和torchvision之间的匹配关系 显卡版本匹配问题...
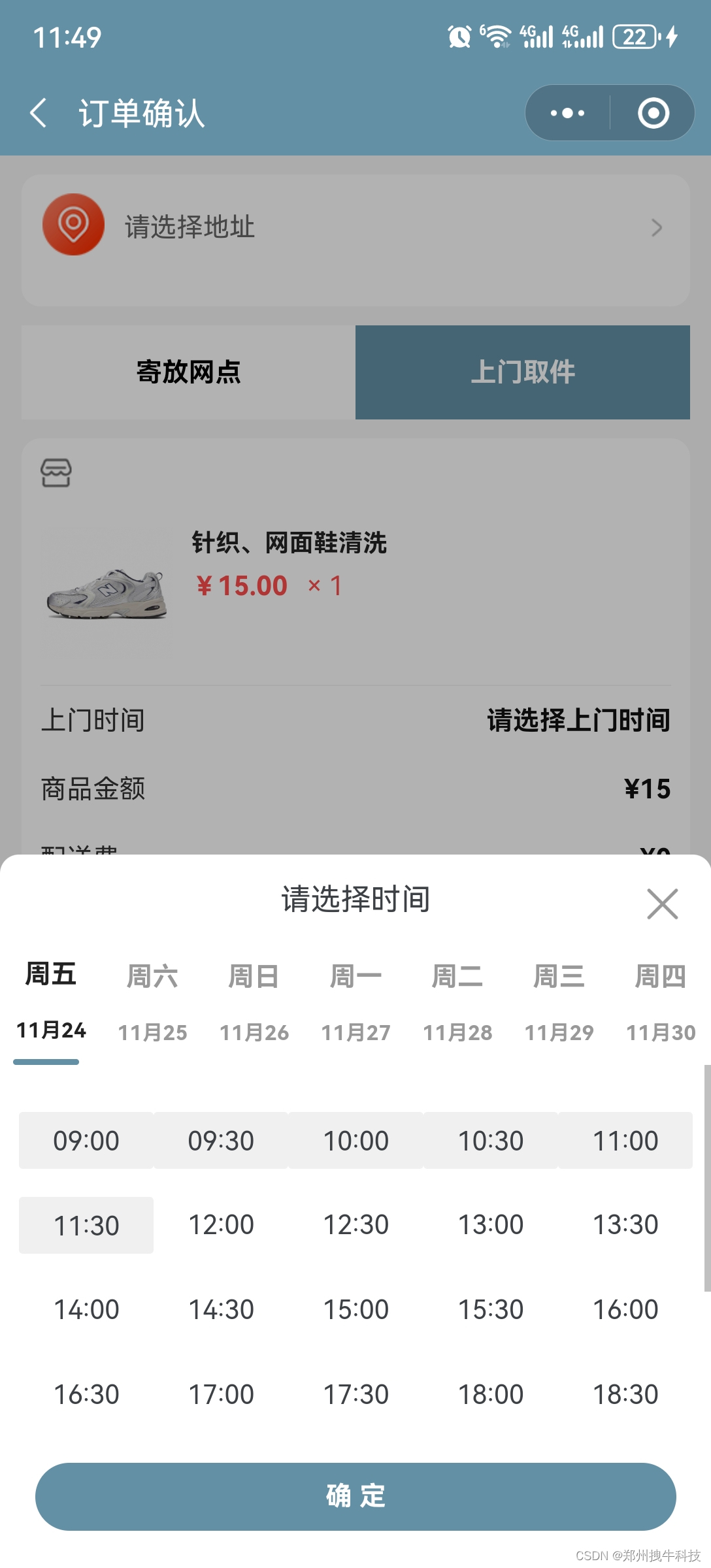
互联网上门洗鞋店小程序
上门洗鞋店小程序门店版是基于原平台版进行增强的,结合洗鞋行业的线下实际运营经验和需求,专为洗鞋人和洗鞋店打造的高效、实用、有价值的管理软件系统。 它能够帮助洗鞋人建立自己的私域流量,实现会员用户管理,实现用户与商家的点…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...