【栈和队列(1)(逆波兰表达式)】
文章目录
- 前言
- 什么是栈(Stack)
- 栈方法
- 栈的模拟实现
- 链表也可以实现栈
- 逆波兰表达式
- 逆波兰表达式在栈中怎么使用
前言
什么是栈(Stack)
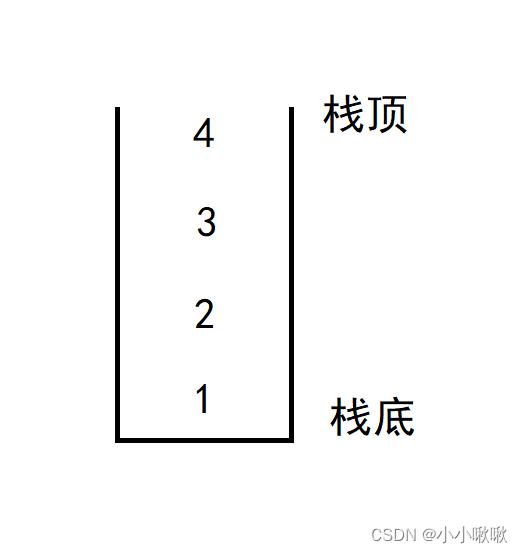
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。遵循先进后出的原则。
类似于:一串羊肉串,后串进去的肉最先被吃到。
底层是数组
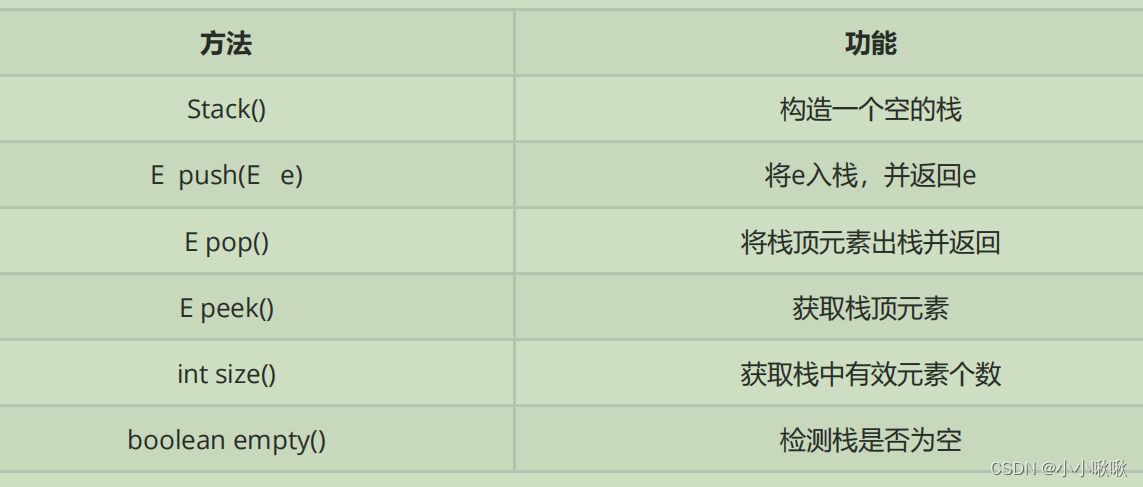
栈方法
栈的模拟实现
//接口
public interface IStack {//放元素void push(int x);//取元素int pop();//查看元素int peek();//栈大小int size();//判断满没满boolean empty();//判断空没空boolean full();
}package stackdemo;
import java.util.Arrays;
//类实现接口
public class MyStack implements IStack{private int[] elem;//栈的底层是一个数组private int usedSize;//有效数据的个数private static final int DEFAULT_CAPACITY = 10;//自定义数组长度//构造方法public MyStack(){elem = new int[DEFAULT_CAPACITY];}//放栈顶元素@Overridepublic void push(int x) {//先检查满没满if (full()){//满了,调用数组拷贝扩容空间elem = Arrays.copyOf(elem,elem.length*2);}//没满就放xelem[usedSize] = x;usedSize++;}//取出栈顶元素@Overridepublic int pop() {if (empty()){//抛异常throw new EmptyException("栈空了!");}int old = elem[usedSize-1];//usedSize往栈底移动一格usedSize--;//相当于删除//如果是引用类型//elem[usedSize] = null;return old;}//查找栈顶的元素,跟pop不一样的是,peek不用删除噢,只是返回栈顶那个元素噢@Overridepublic int peek() {if (empty()){//抛异常throw new EmptyException("栈空了!");}return elem[usedSize-1];//}/算栈的大小@Overridepublic int size() {return usedSize;}//判断栈空没空@Overridepublic boolean empty() {return usedSize == 0;}//判断栈满没满@Overridepublic boolean full() {if (usedSize == elem.length){return true;}return false;}
}
//抛异常
public class EmptyException extends RuntimeException {//构造方法public EmptyException(String msg){super(msg);}
}
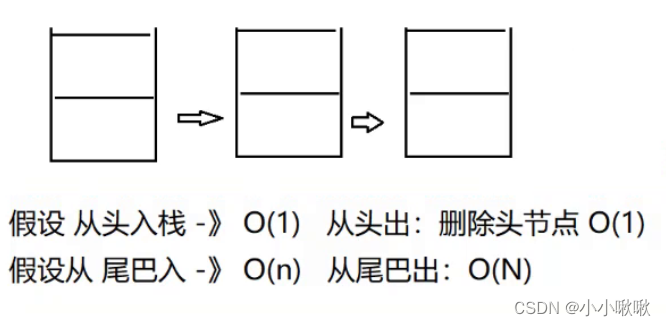
链表也可以实现栈
单链表
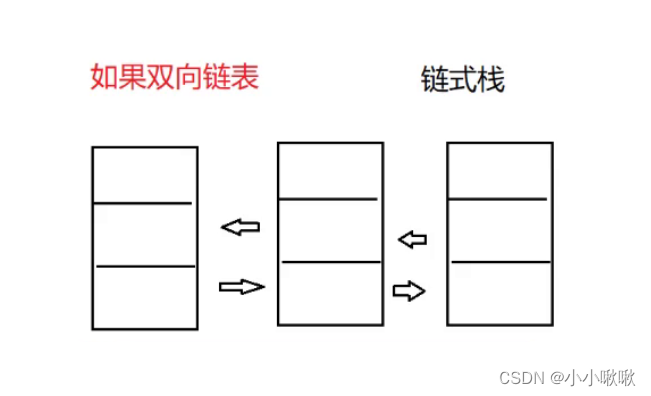
双向链表
从头入 从头出都可以
-
若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是()
A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1
答案:C -
一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺
序是( )。
A: 12345ABCDE B: EDCBA54321 C: ABCDE12345 D: 54321EDCBA
答案:B
逆波兰表达式
下面举的例子是后缀表达式,就是把符号移到括号右边。
怎么转换成逆波兰表达式
逆波兰表达式在栈中怎么使用
1.把式子转换成逆波兰表达式后
2.遇到数字就放栈里面
2.当遇到非数字字符,取出栈里面最顶上的两个元素,第一个元素放在字符右边,第二个放左边。
3.得到的结果又放进栈里面
4.再继续上面步骤
逆波兰表达式演示视频
class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for(String s : tokens) {//不是操作符就是数字if (!isOperation(s)) {stack.push(Integer.parseInt(s));} else {int num2 = stack.pop();int num1 = stack.pop();switch (s) {case "+":stack.push(num1 + num2);break;case "-":stack.push(num1 - num2);break;case "*":stack.push(num1 * num2);break;case "/":stack.push(num1 / num2);break;}}}return stack.pop();}private boolean isOperation(String s) {if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {return true;//是返回true}//不是返回falsereturn false;}
}
相关文章:

【栈和队列(1)(逆波兰表达式)】
文章目录 前言什么是栈(Stack)栈方法栈的模拟实现链表也可以实现栈逆波兰表达式逆波兰表达式在栈中怎么使用 前言 什么是栈(Stack) 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶࿰…...
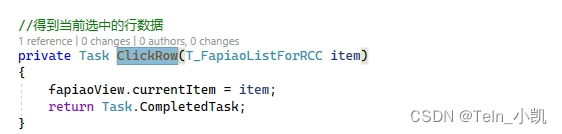
Blazor Table 实现获取当前选中行的功能
这里需要使用到OnClickRowCallBack事件 后台使用案例...
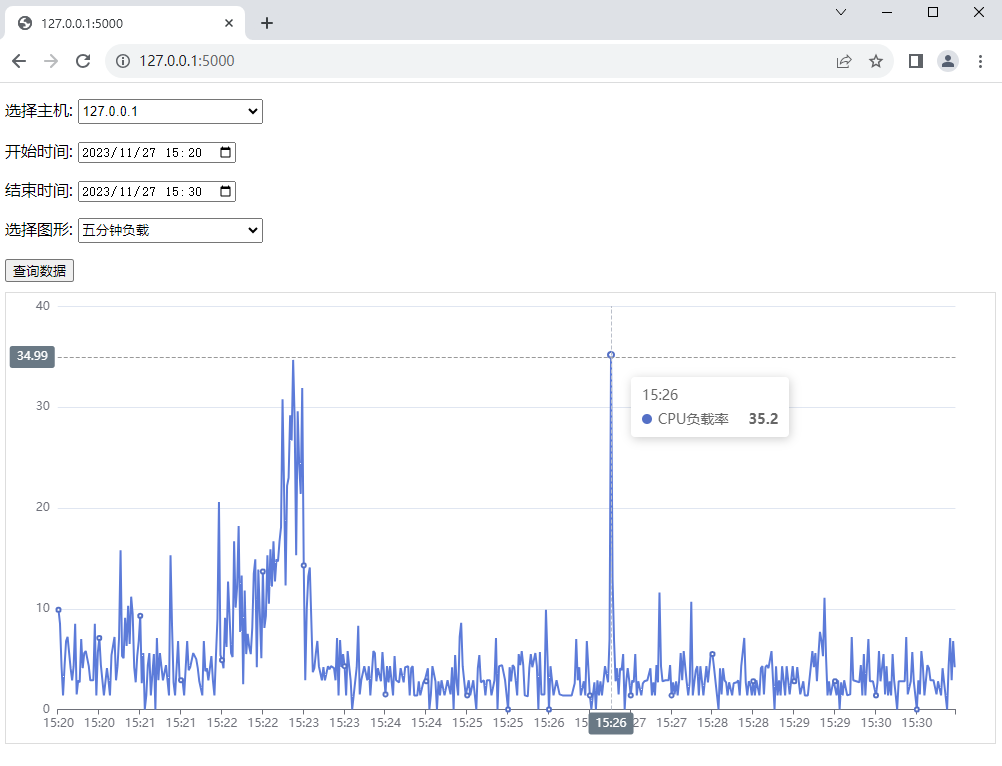
Flask Echarts 实现历史图形查询
Flask前后端数据动态交互涉及用户界面与服务器之间的灵活数据传递。用户界面使用ECharts图形库实时渲染数据。它提供了丰富多彩、交互性强的图表和地图,能够在网页上直观、生动地展示数据。ECharts支持各种常见的图表类型,包括折线图、柱状图、饼图、散点…...

【漫谈】信创
近些年来,自主创新绝对是高频词汇。 以往是供应链、芯片领域,现在终于到了信息领域。 近期,从上至下、从中央到地方、从政府到国企,各层面、各行业、各领域都在提及“信创”。 信创是个大工程,从计算机通用处理器、…...

linux wget --no-check-certificate
如果您希望每次使用wget命令时都跳过SSL证书检查,可以将–no-check-certificate参数添加到wget的默认配置文件中。 请按照以下步骤进行操作: vi ~/.wgetrc# 插入内容 check_certificate off保存并关闭文件。 现在,wget命令将在每次使用时自…...

mysql命令行连接数据库
有时项目连接不上数据库,报错鉴权失败,先用mysql工具连接下,容易发现问题。 直接输入mysql看是否已安装,如果没有就安装下。 # 注:直接mysql就行,不用-cli也不用-client,也不用-server…...

计算机丢失vcomp140.dll是什么意思,如何解决与修复(附教程)
vcomp140.dll缺失的5种解决方法以及vcomp140.dll缺失原因 引言: 在日常使用电脑的过程中,我们可能会遇到一些错误提示,其中之一就是“vcomp140.dll缺失”。这个错误提示通常出现在运行某些程序或游戏时,给使用者带来了困扰。本文…...
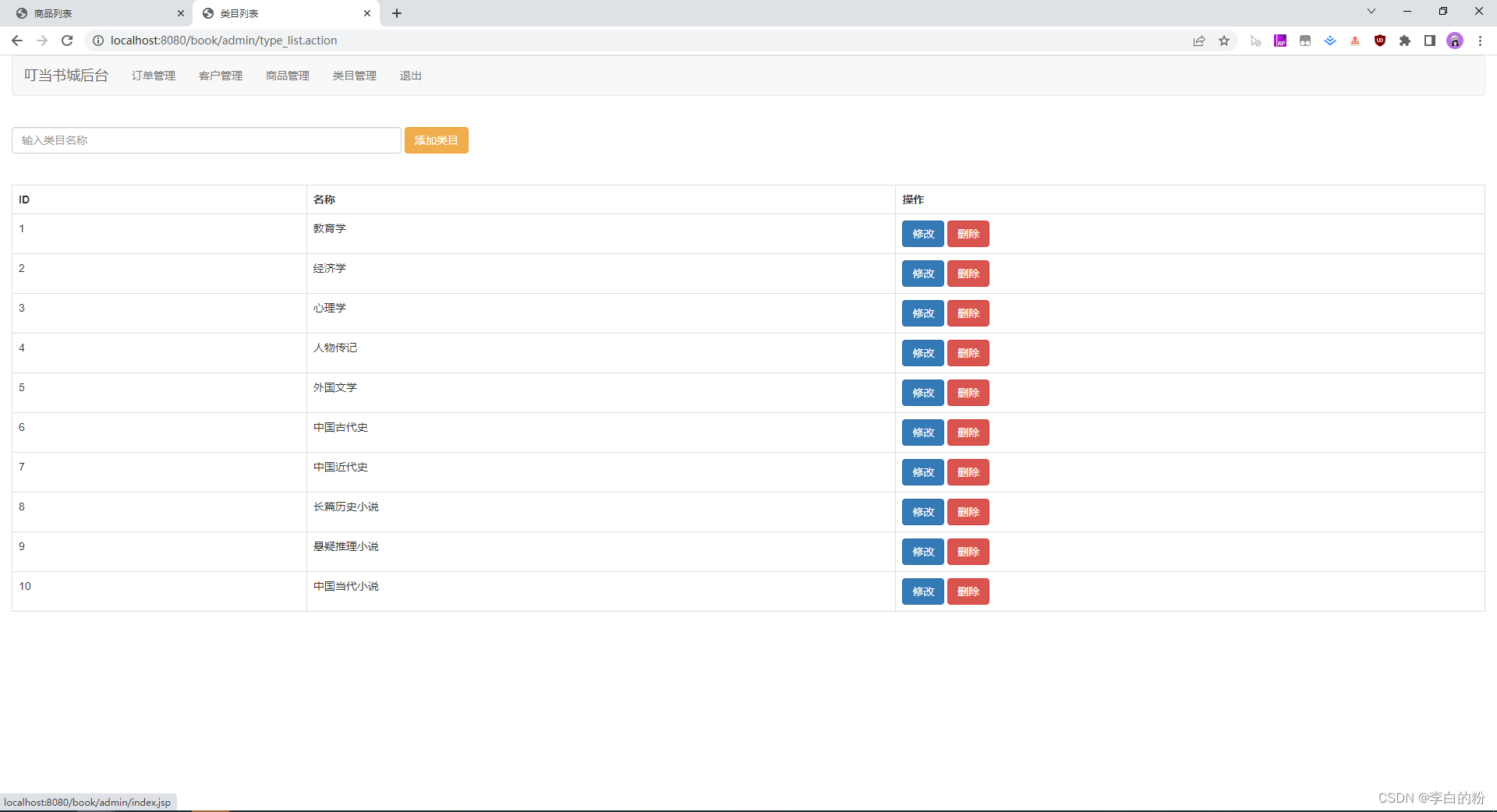
基于SSM实现的叮当书城
一、系统架构 前端:jsp | jquery | layui 后端:spring | springmvc | mybatis 环境:jdk1.7以上 | mysql | maven 二、代码与数据库 三、功能介绍 01. 系统首页 02. 商品分类 03. 热销 04. 新品 05. 注册 06. 登录 07. 购物车 08. 后台-首页 …...

python基础练习题库实验5
文章目录 题目1代码实验结果题目2代码实验结果题目3代码实验结果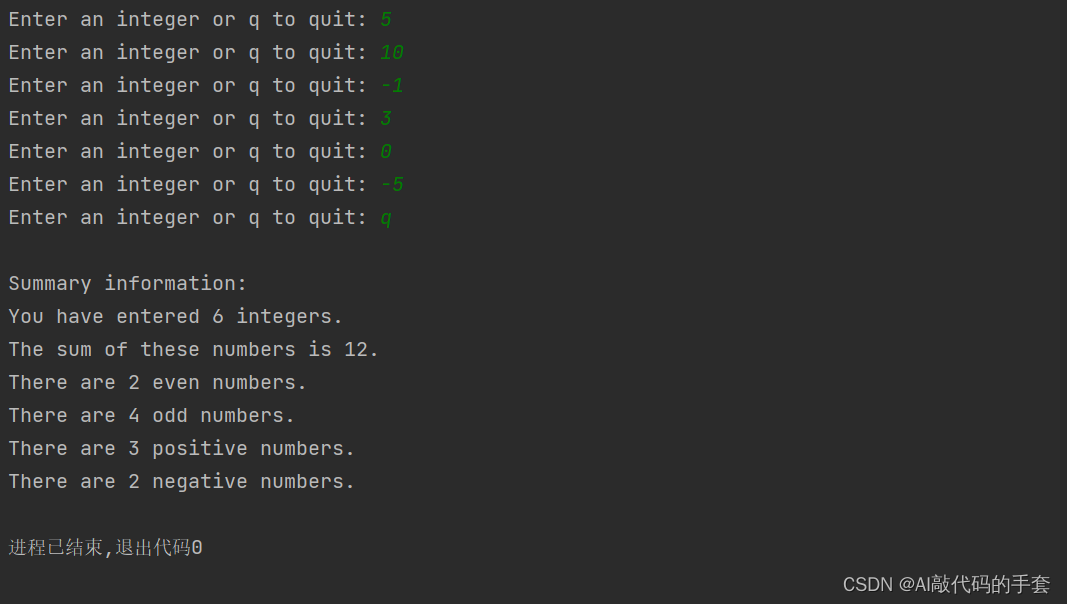题目4代码实验结果题目总结题目1 编写一个程序,使用while循环语句和字符串格式显示以下精确输出。 例如: …...
)
JS手写instanceof(内含源码与详解)
前言 本文主要讲解JavaScript如何手写一个简易的instanceof,从而实现数据类型判断的作用.那么好,本文正式开始. instanceof作用 instanceOf的作用就是用来判断JavaScript中的数据类型是否是开发所输入的那种, 语法格式:obj instanceof objtype 左侧就是要判断的数据,而右侧就…...
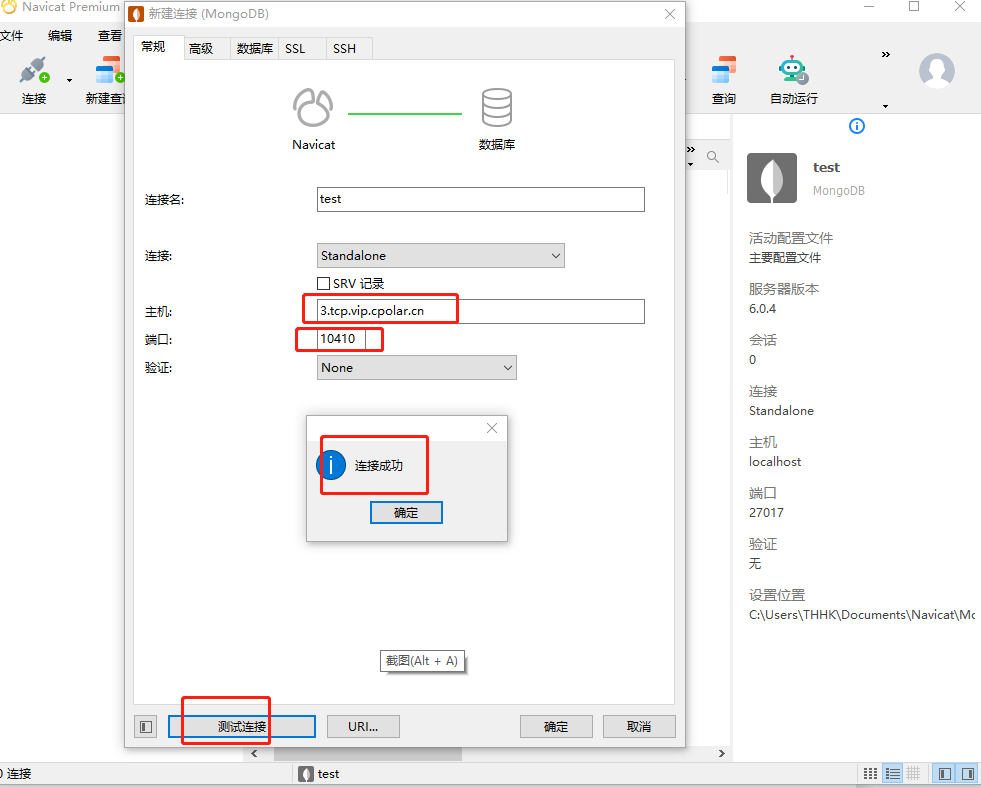
无公网IP下,如何实现公网远程访问MongoDB文件数据库
文章目录 前言1. 安装数据库2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射2.3 测试随机公网地址远程连接 3. 配置固定TCP端口地址3.1 保留一个固定的公网TCP端口地址3.2 配置固定公网TCP端口地址3.3 测试固定地址公网远程访问 前言 MongoDB是一个基于分布式文件存储的数…...

初始化的内容写到析构函数中。。。。。。。
大概是,把应该在构造函数中初始化的堆栈窗体代码写到了析构函数中。。。。 不是因为没掌握构造/析构,而是。。。。 检查了四十多分钟没检查出来。。 被自己蠢哭。 #include "widget.h"Widget::Widget(QWidget *parent): QWidget(parent) { }…...

git 使用过程错误集合
文章目录 1、git-credential-manager-core was renamed to git-credential-manager2、credential-manager-core is not a git command. See git --help. 1、git-credential-manager-core was renamed to git-credential-manager 出现以下提示建议尽快更新您的 Git 配置以使用新…...

Lua判断字符串包含另一个字符串
string.find(“原字符串”,“目标字符串”) 返回这个子串的起始索引和结束索引,否则就会返回nil local index sting.find("ABCD",AB) --结果 1 2 if(index ~ nil)return true endstring.match(“原字符串”,“目标字符串”) local result string.mat…...

二叉树之推排序(升序)
目录 1.思路1.1大堆的建立方法1.2排序的方法 2.代码实现以及测试代码 1.思路 如何将一个堆进行排序,并变成升序?首先,如果要完成升序,那我们可以建立一个大堆,因为大堆可以选出一个最大的值放在堆的最上面,…...
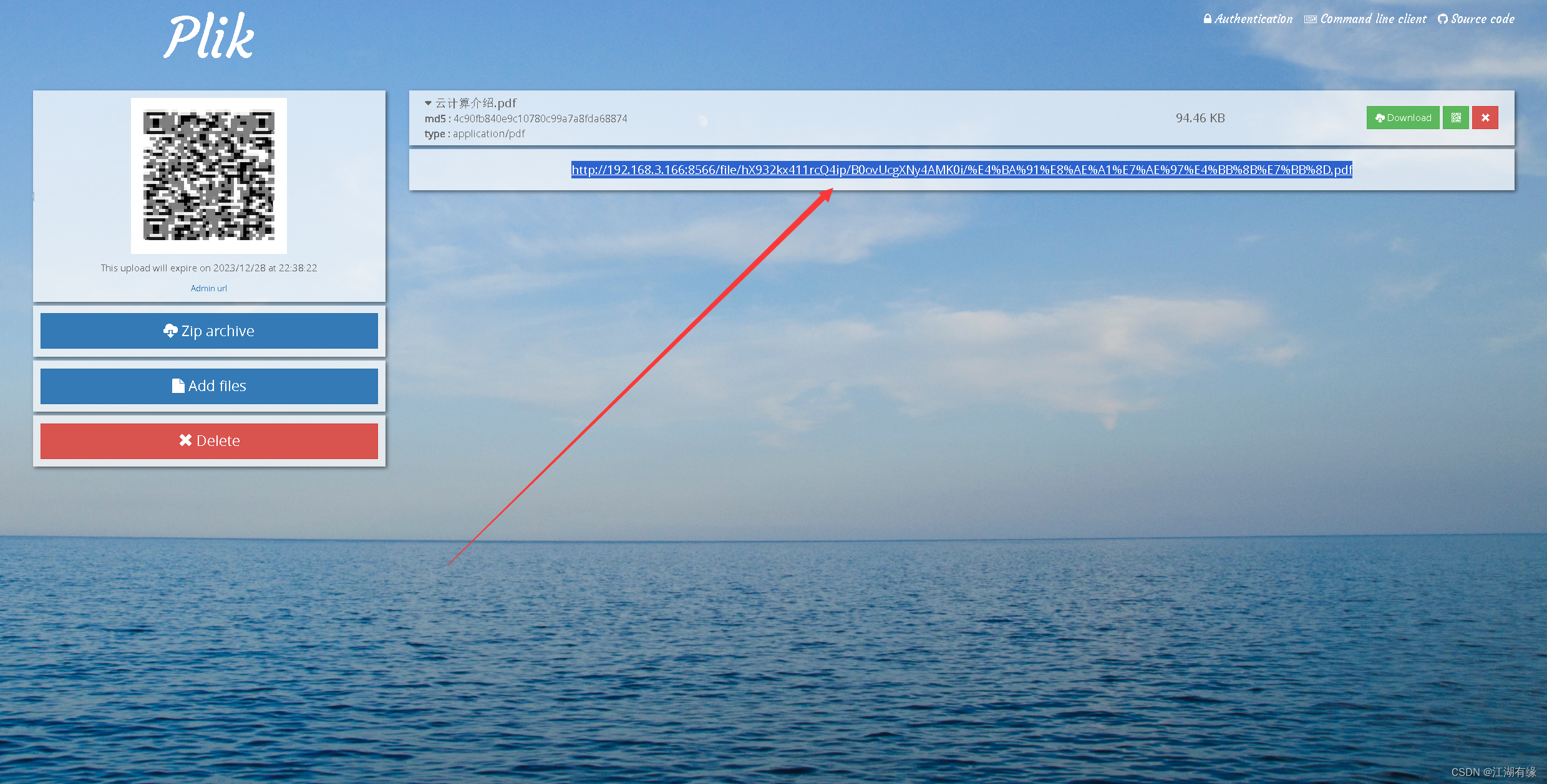
【Docker项目实战】使用Docker部署Plik临时文件上传系统
【Docker实战项目】使用Docker部署Plik 临时文件上传系统 一、Plik介绍1.1 Plik简介1.2 Plik特点 二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载Plik镜像五、部署Plik临时…...

JsonRPC协议详解(协议介绍、请求示例、响应示例)
JsonRPC协议详解 文章目录 JsonRPC协议详解什么是RPC?什么是JsonRPC?JsonRPC详解请求示例响应示例成功和失败响应示例参数的数据类型 结束语 什么是RPC? RPC(远程过程调用)是一种用于实现分布式系统中不同进程或不同计…...
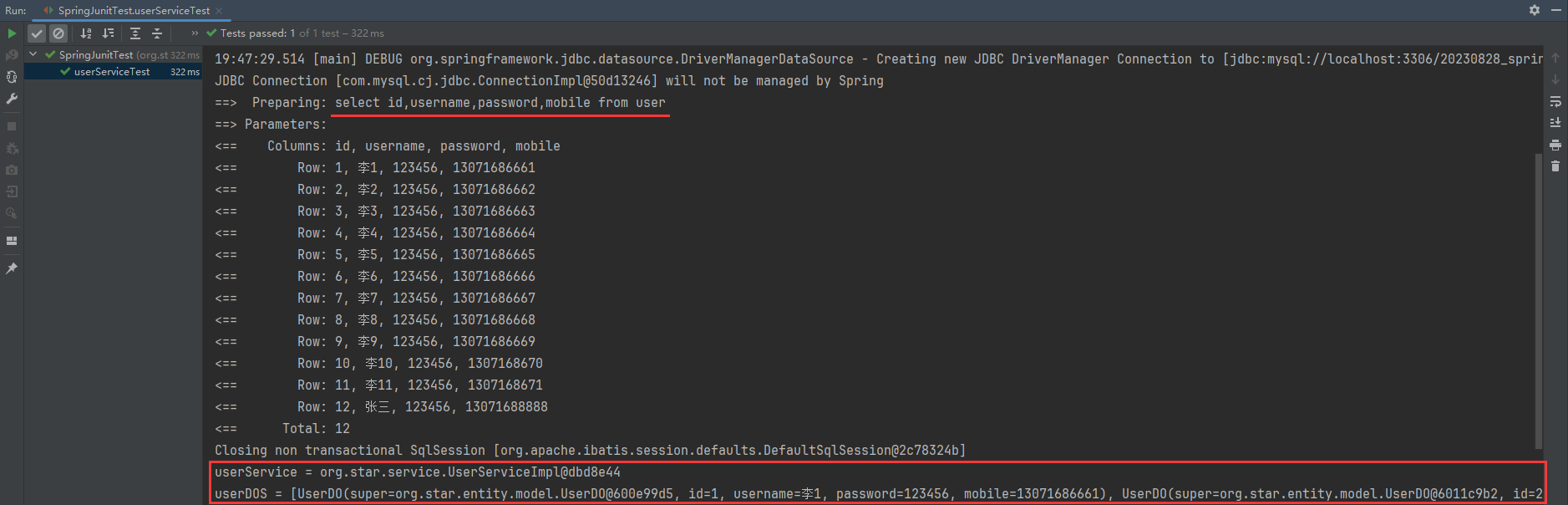
系列六、Spring整合单元测试
一、概述 Spring中获取bean最常见的方式是通过ClassPathXmlApplicationContext 或者 AnnotationConfigApplicationContext的getBean()方式获取bean,那么在Spring中如何像在SpringBoot中直接一个类上添加个SpringBootTest注解,即可在类中注入自己想要测试…...
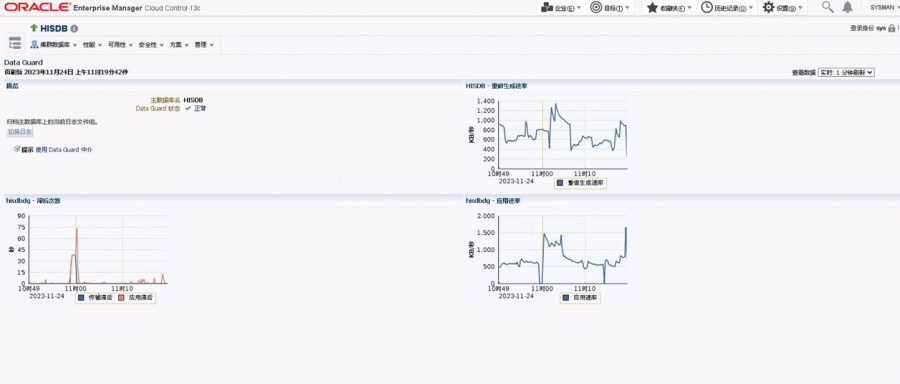
如何把 Oracle 19C RAC+DG加入到ORACLE EM 13C监控
平时见ORACLE 19c rac single dg的部署很多了,ORACLE em 13c 的安装也很多了,但如何把手工部署的oracle 19c rac dg 添加到em 13c 中去,让EM13C 来实现对RACDG的监控,主要是DG的EM13C的监控,还没有看到,大部分都是直接…...

Go 编程语言详解:用途、特性、与 Python 和 C++ 的比较
什么是Go? Go是一个跨平台、开源的编程语言Go可用于创建高性能应用程序Go是一种快速、静态类型、编译型语言,感觉上像动态类型、解释型语言Go由Robert Griesemer、Rob Pike和Ken Thompson于2007年在Google开发Go的语法类似于C Go用于什么? Web开发&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
