高等数学零基础篇复习笔记
预备章 零基础高等数学入门知识
第一节 集合、运算与关系

第二节 三角函数与反三角函数
三角函数的公式
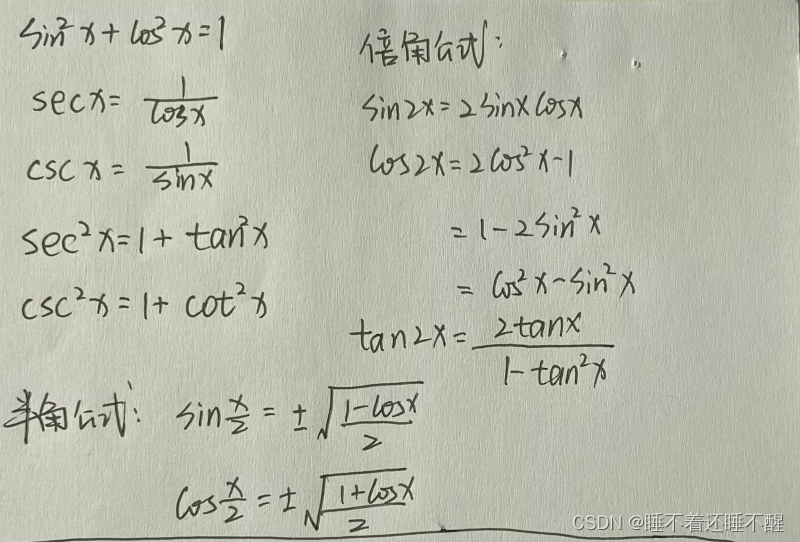
反三角函数
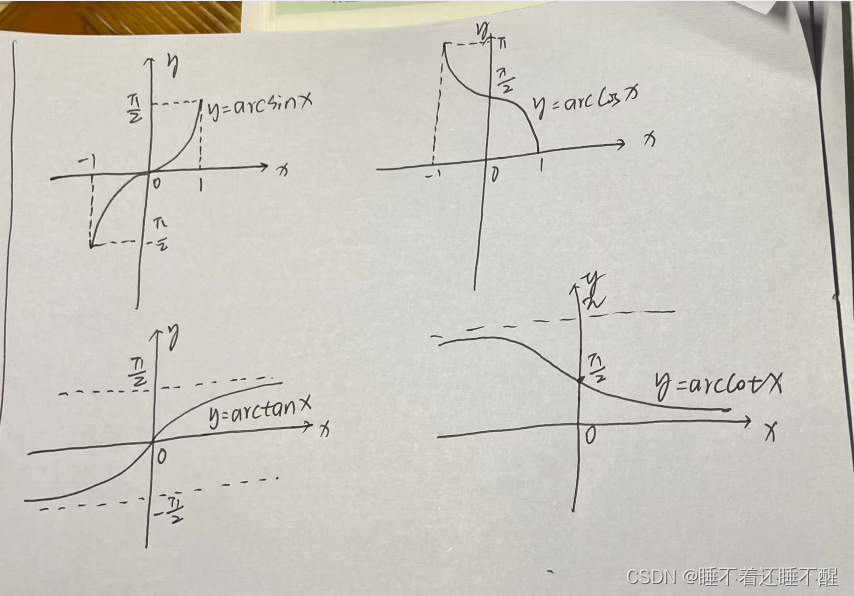
第三节 常见不等式及数列

划重点
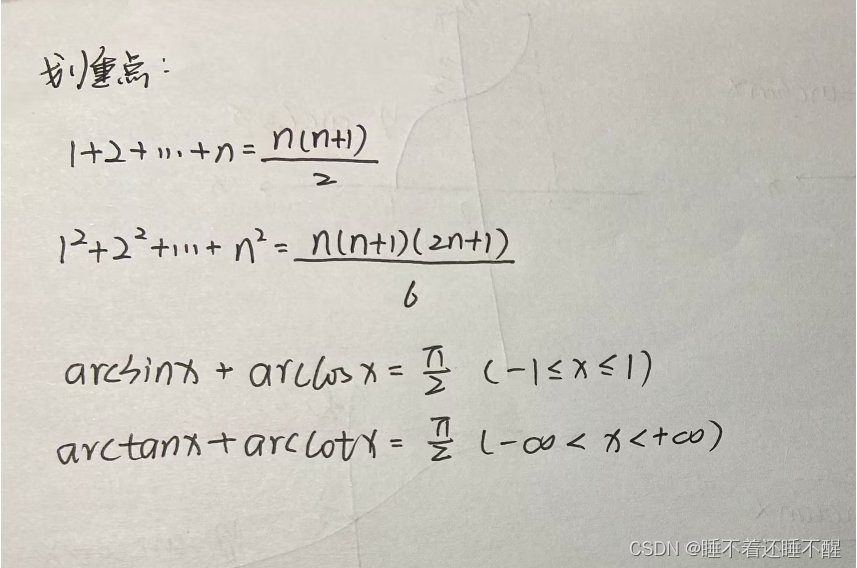
第一章 函数、极限与连续
第一节 函数及函数的初等特性
特殊函数

反函数

函数的初等特性
①有界性
②奇偶性
偶函数图像关于y轴对称,奇函数图像关于原点对称
奇函数与偶函数之积为奇函数,奇函数与奇函数之积为偶函数
③单调性
④周期性
第二节 极限
基本性质
极限存在的充要条件是左右极限存在且相等

极限的基本性质
定理一(唯一性):无论是数列极限还是函数关于自变量各种趋向,若极限存在必唯一

定理二(有界性):极限存在必有界,反之不成立

定理三(保号性):

证明如下:

第三节 无穷小与无穷大
基本概念

无穷小的基本性质
1.有限个无穷小之和或差仍为无穷小
2.有界函数与无穷小之积仍为无穷小
3.常数与无穷小之积仍为无穷小
4.极限与无穷小的关系:
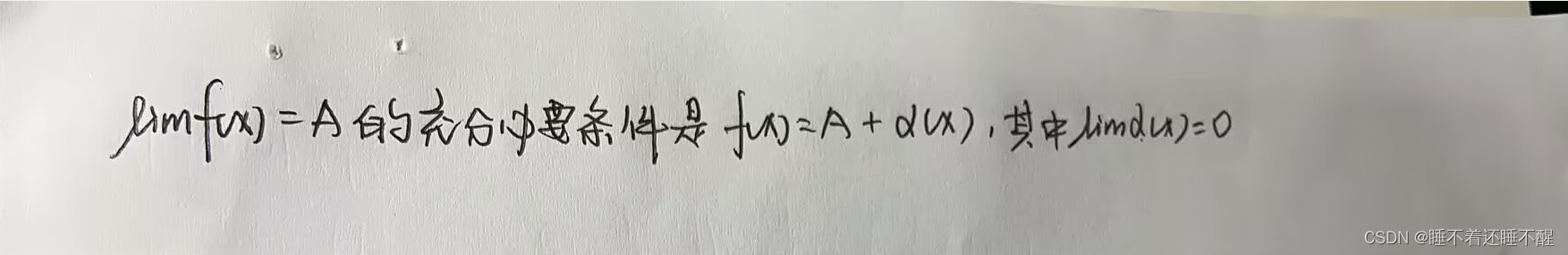
协助证明:

无穷小的等价性质

第四节 极限存在准则与重要极限
极限存在定理
夹逼定理
定理:

证明:

例题:


单调有界定理

例题:


两个重要极限

例题: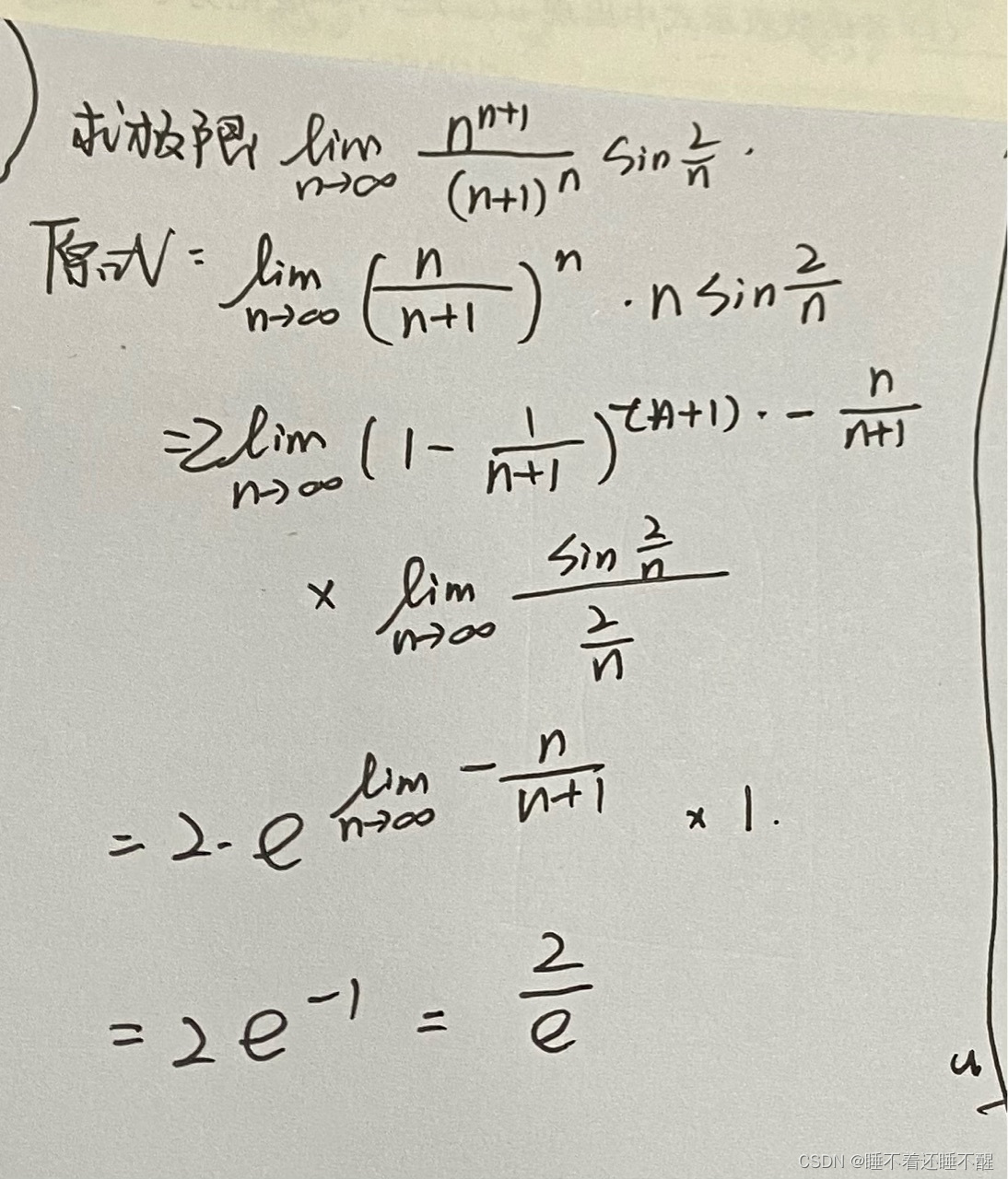
第五节 连续与间断
连续

间断

闭区间上连续函数的性质

章节重点习题
题型一 不定型极限计算

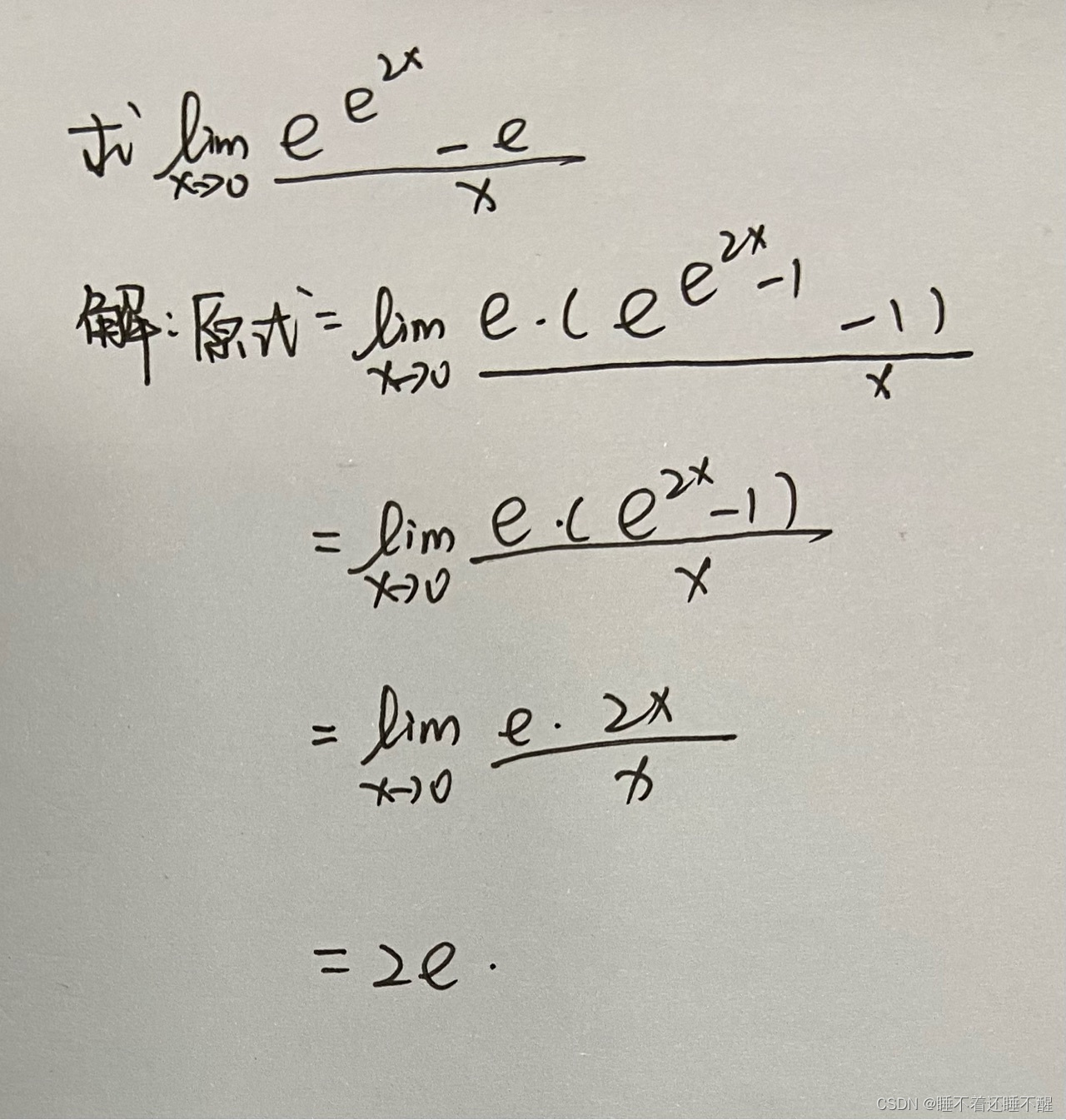
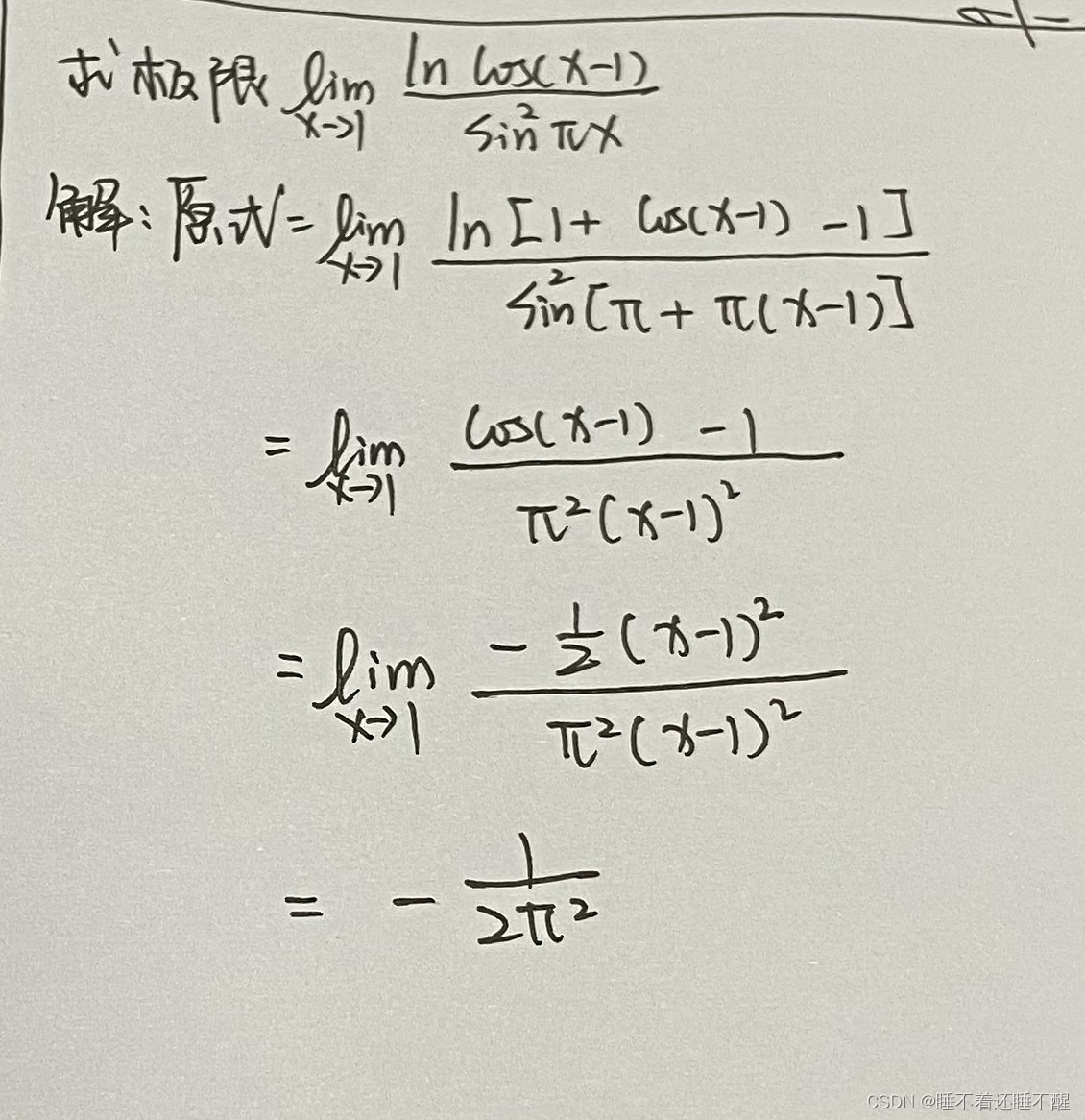




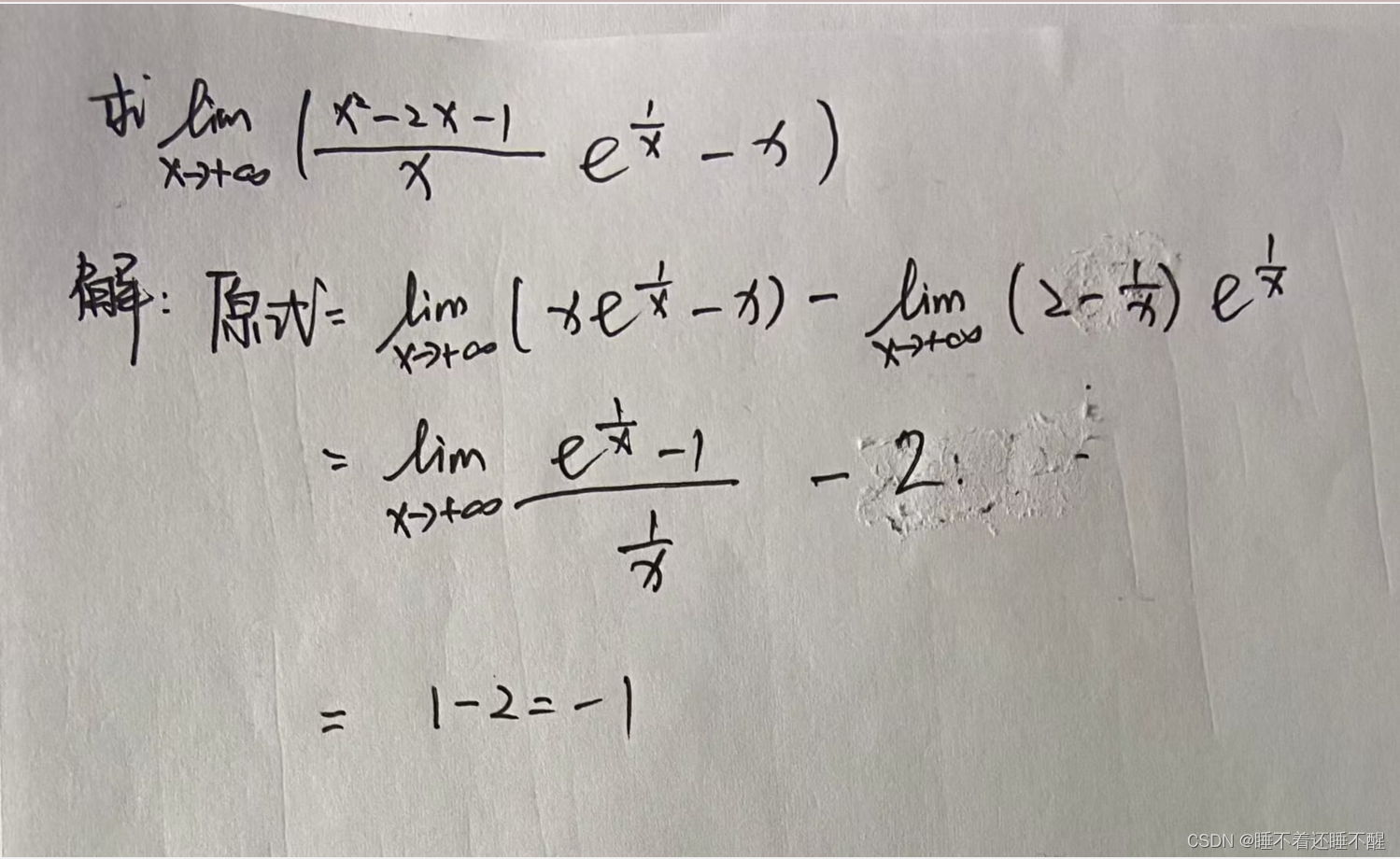
题型二 利用夹逼定理求极限
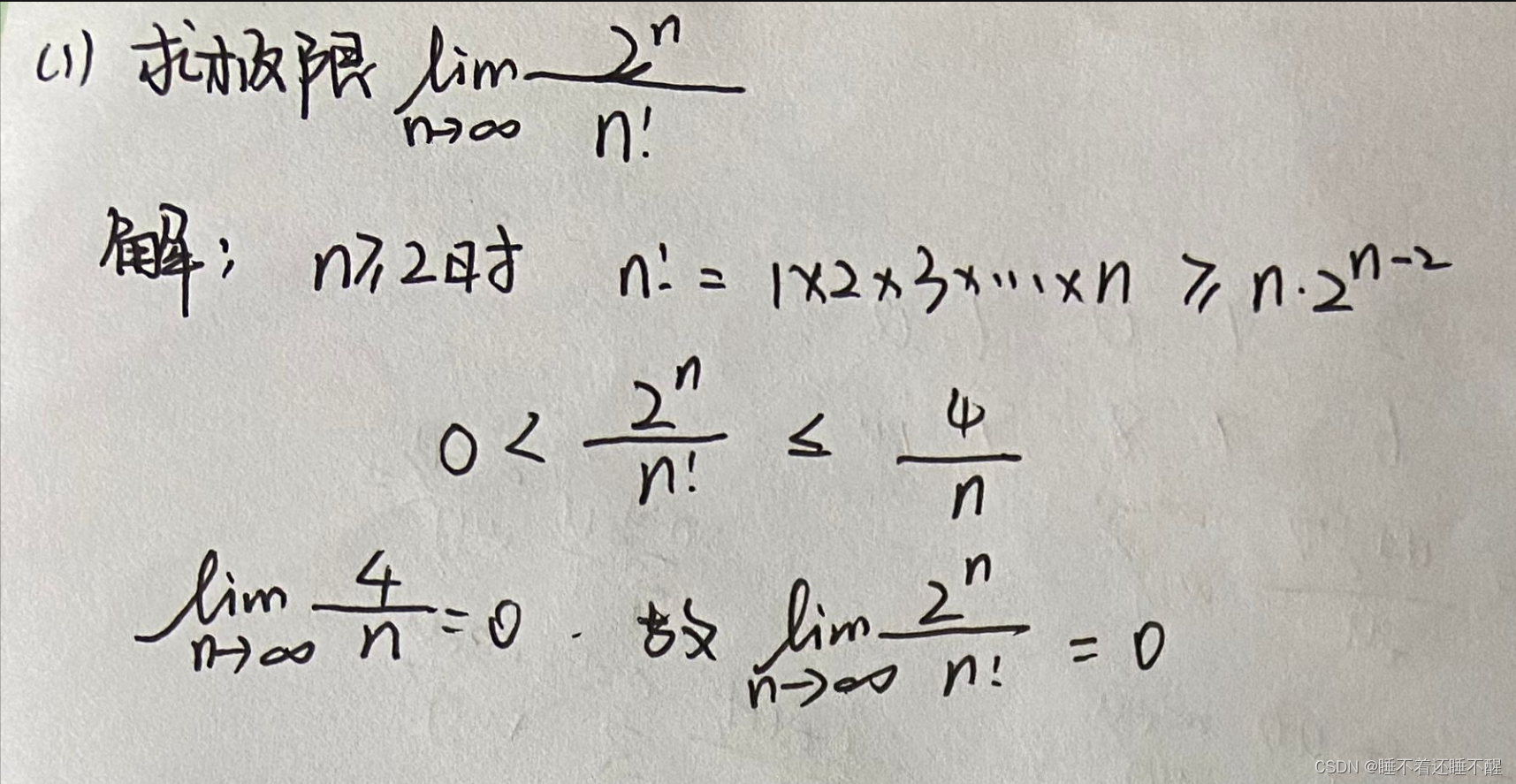
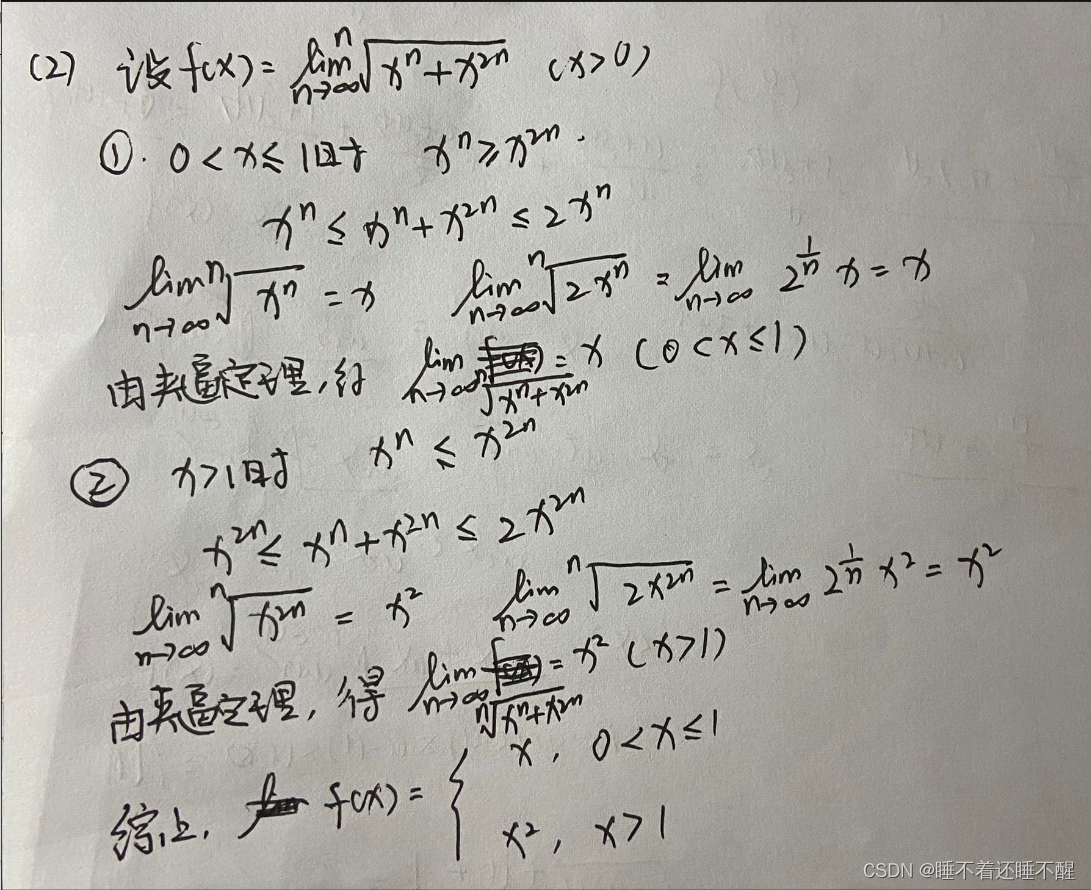
题型三 无穷小的比较


题型四 间断点判断

第二章 导数与微分
第一节 导数与微分的基本概念与性质
基本概念
导数:

微分:
函数f(x)在点x处可导的充要条件为f(x)在点x可微
求导基本工具
求导基本公式:
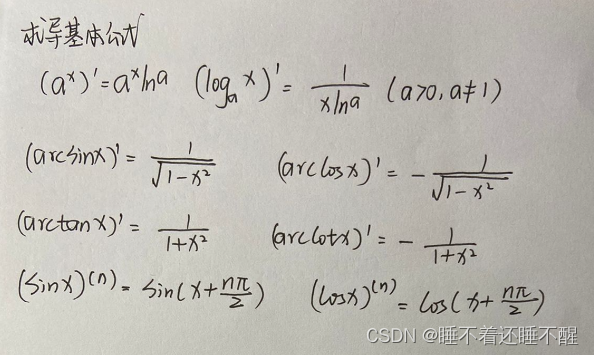
导数的四则运算:

链式法则:

反函数的导数:

第二节 隐函数及参数方程确定的函数的导数
隐函数的导数
F(x,y)=0确定y是x的函数,求y对x的各阶导数,只要将y看成x的表达式即可。
参数方程确定的函数的导数

章节重点习题
题型一 用导数定义求导及判断可导性


第三章 中值定理与导数的应用
第一节 中值定理与洛必达法则
费马定理

罗尔定理

拉格朗日中值定理

柯西中值定理

泰勒定理

常见麦克劳林公式:
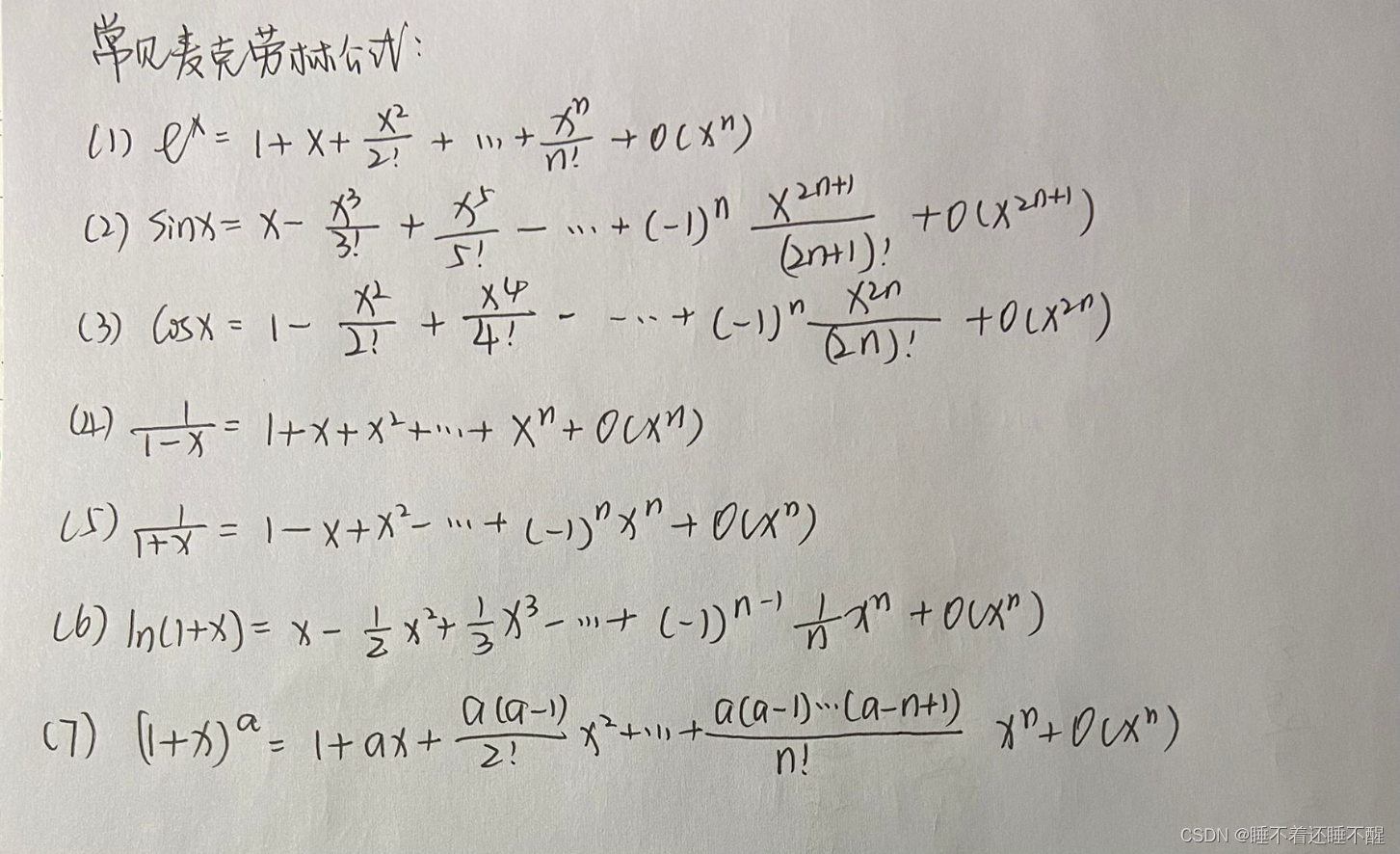
补充例题:构造函数证明等式


洛必达法则
适用情况:零比零型、无穷比无穷型
说明:使用洛必达法则后没有极限,只能说明洛必达法则对该题不适用,不能说明极限不存在
基本原理:分子分母同时求导得到的极限等于原分子比分母的极限
第二节 导数的应用
求函数极值点的步骤
注明:首先要看定义域

极值判定定理第二充分条件

函数图像的凹凸性

凹凸性判别法:

判别法证明:

曲线的渐近线

弧微分与曲率

章节重点习题
题型一 中值定理及应用


题型二 不等式的证明

题型三 曲线的渐近线

第四章 不定积分
第一节 不定积分的基本概念与性质
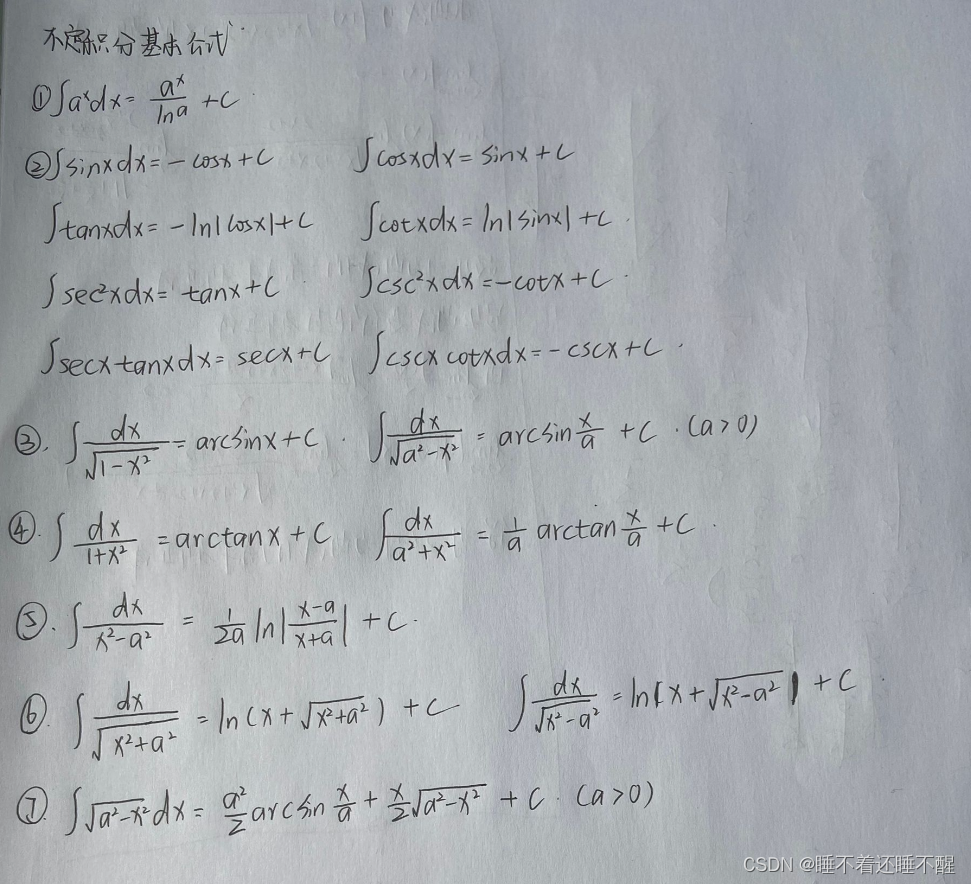
第二节 不定积分的积分法
第一类换元积分
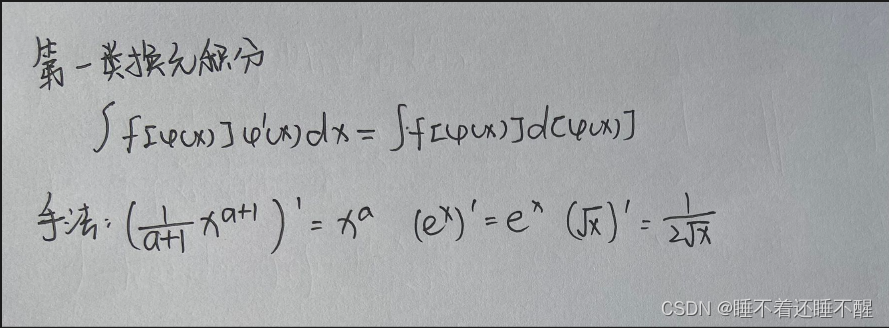
典型例题:

第二类换元积分

典型例题:

分部积分法

第三节 两类特殊函数的不定积分
有理函数的不定积分

多项式的除法:

三角函数有理式的不定积分

典型例题:

章节重点习题
题型一 函数与原函数问题

题型二 第一类换元积分法

题型三 第二类换元积分法

第五章 定积分及应用
第一节 定积分的基本概念与一般性质

积分中值定理的证明:

tips:

第二节 定积分基本定理与定积分的特殊性质
变积分限的函数

定积分的基本定理
定理一:

划重点:

定理二:

定积分的特殊性质
对称区间的定积分性质

三角函数的定积分性质


周期函数的定积分性质

第三节 反常积分
反常积分的定义

区间无限的反常积分




无界函数的反常积分



第四节 定积分的几何应用
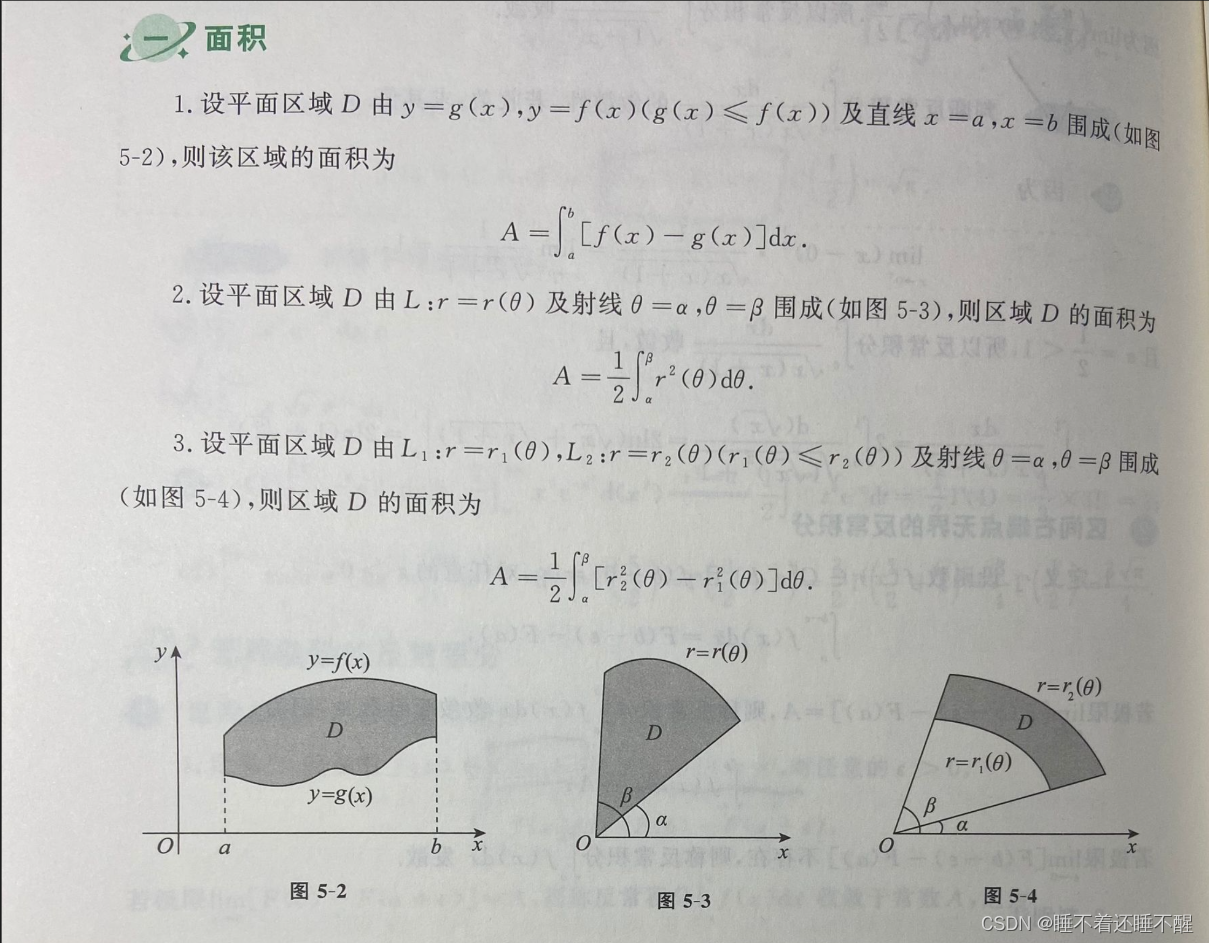

章节重点习题
题型一 定积分的基本性质

题型二 定积分的常规计算
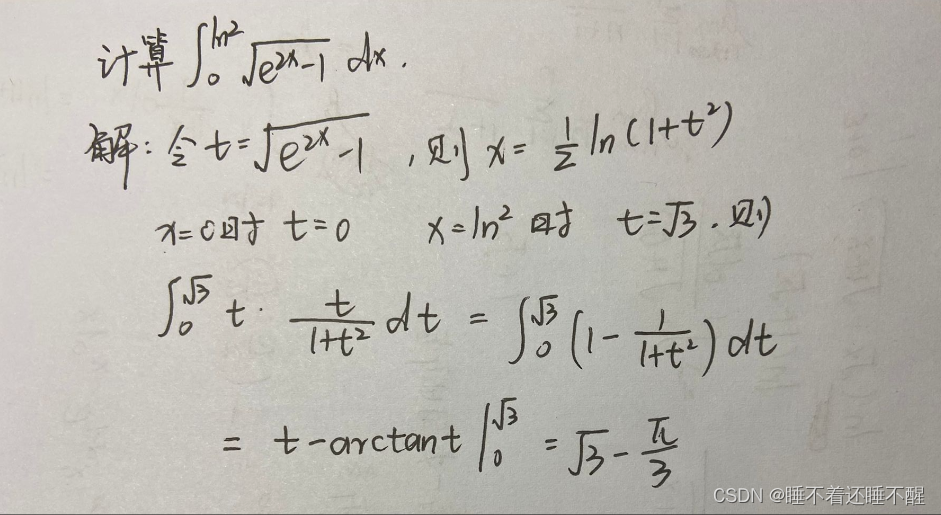
第六章 微分方程
第一节 微分方程的基本概念与一阶微分方程
微分方程的基本概念

划重点:

一阶微分方程的种类及解法
可分离变量的微分方程

齐次微分方程

一阶齐次线性微分方程

一阶非齐次线性微分方程

第二节 可降阶的高阶微分方程
情况一:

情况二:

情况三:

第三节 高阶线性微分方程
基本概念

二阶线性微分方程的解的结构

二阶常系数线性微分方程的解
二阶常系数齐次线性微分方程

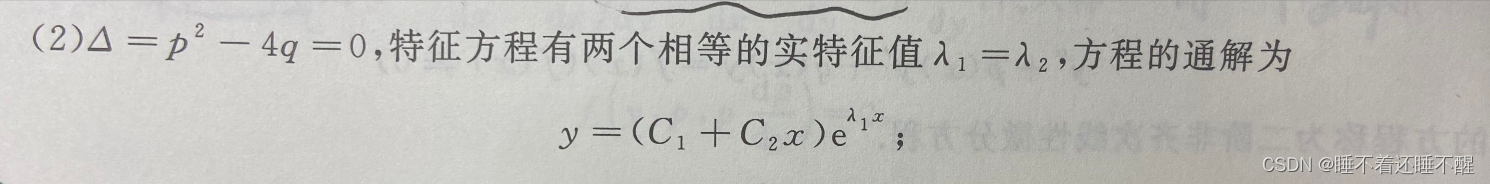

二阶常系数非齐次线性微分方程



第七章 多元函数微分学
第一节 多元函数微分学的基本概念
偏导数

高阶偏导数

有界闭区域上二元连续函数的性质

第二节 全微分
全微分的定义

划重点:

二元函数连续、可偏导、可微之间的关系
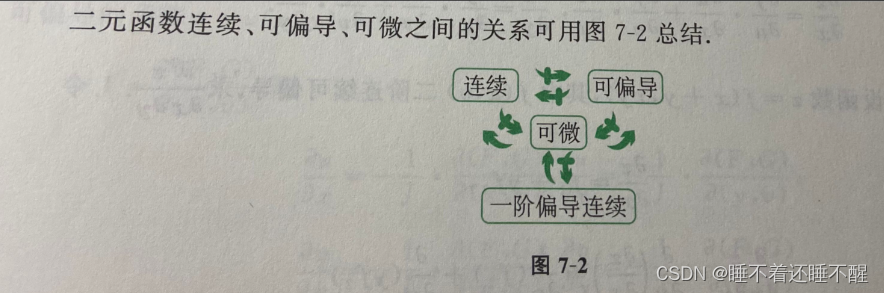
第三节 多元函数求导法则
复合函数求导法则

隐函数(组)确定的函数求导法则


第四节 多元函数的极值
无条件极值

条件极值

章节重点习题
题型一 多元函数的基本概念与性质

题型二 显函数、复合函数及隐函数求偏导

题型三 多元函数的极值


第八章 二重积分
第一节 二重积分的概念与性质

二重积分的对称性

章节重点习题

高等数学零基础篇复习到此结束,祝各位友友一战成硕~~
相关文章:

高等数学零基础篇复习笔记
预备章 零基础高等数学入门知识 第一节 集合、运算与关系 第二节 三角函数与反三角函数 三角函数的公式 反三角函数 第三节 常见不等式及数列 划重点 第一章 函数、极限与连续 第一节 函数及函数的初等特性 特殊函数 反函数 函数的初等特性 ①有界性 ②奇偶性 偶函数图像…...

CentOS 系列:CentOS 7文件系统的组成
CentOS 7文件系统的组成 文件系统的组成Linux的一些重要目录文件和目录名主机名文件权限绝对路径和相对路径绝对路径相对路径 文件系统的组成 一切从根开始 文件路径中只有第一个/是根目录,后面的/是分隔符 文件名区分大小写 除斜线(/)以外,其他的字符…...

String转Date,Date转String
源码: Date currentTime new Date();System.out.println("currentTime:"currentTime);SimpleDateFormat formatter new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");String dateString formatter.format(currentTime);System.out.println(&quo…...

大坝安全监测的内容及作用
大坝安全监测是指对大坝水雨情沉降、倾斜、渗压以及大坝形状特征有效地进行监测,及时发现潜在的安全隐患和异常情况,以便大坝管理人员能够做出科学决策,以确保大坝安全稳定运行。 大坝安全监测的主要内容 1.表面位移监测:监测大坝…...

Maven——Maven发展历程
本帖主要介绍以下内容: 什么是Maven为什么需要MavenMaven与极限编程 1、什么是Maven Maven这个词可以翻译为“知识的积累”,也可以翻译为“专家”或“内行”。Maven是跨平台的项目管理工具。作为Apache组织中的一个颇为成功的开源项目,Mav…...

Python与设计模式--迭代器模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...

【NGINX--8】HTTP/2
1、基本配置 想要利用 HTTP/2。 在 NGINX 服务器上启用 HTTP/2: server {listen 443 ssl http2 default_server;ssl_certificate server.crt; ssl_certificate_key server.key;# ... }详解 要启用 HTTP/2,您只需要将 http2 参数添加到 listen 指令即可…...
webpack项目工程初始化
一、初始化项目 默认系统已经安装node //初始化 pnpm init//安装webpack pnpm i -D webpack webpack-cli 新建一个index.html的入口文件 新建一个src文件存放js代码,src里面新建一个index.js package.josn配置打包命令 {"name": "webpack-cs&q…...

08-学成在线项目中统一异常处理的规范
项目中的异常处理 规范异常类型 在Service类的业务方法中有很多的参数合法性校验,当请求参数不合法的时候会抛出异常,但此时异常信息只会在控制台输出,前端界面并不会提示用户 实际开发中前端和后端需要做一些约定: 一般将错误提示信息统一以json格式返回给前端,以HTTP状态码…...

解析生效探测方法
linux dig命令 1.最常用的查询命令 dig baidu.com2 . 根据记录类型进行查询,比如MX,CNAME,NS,PTR等,只需将类型加在命令后面即可。 dig a.shifen.com ns3 . 指定域名DNS服务器测试解析是否生效的命令,以…...

【科技素养】蓝桥杯STEMA 科技素养组模拟练习试卷11
单选题 1、在阅读文章和接受信息时注意区分事实和观点十分重要。事实(或称为命题)不同于观点的一个主要特征是 A、可以被证实或证伪 B、是准确无误的 C、是正式的表达 D、表达了个人看法 答案:A 2、现代意义的知识产权是在多数国家都受…...
视频集中存储/磁盘阵列EasyCVR平台黑名单异常解决步骤是什么?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...

Spring Boot + MyBatis-Plus实现数据库读写分离
文章目录 1. 引言2. MyBatis-Plus简介3. 准备工作4. 配置数据源5. 配置MyBatis-Plus6. 创建实体类和Mapper接口7. 编写Service8. 控制器层9. 测试10. 数据库读写分离的原理11. 拓展11.1. 动态数据源11.2. 多数据源事务管理11.3. 多租户支持 12. 总结 🎉Spring Boot …...
)
数据同步异常处理,数据同步重试机制(Java)
一、应用场景 在数据同步时,偶尔会出现代码异常之外的问题。例如网络异常、服务器断电… 如果在以上异常片段中,原始数据库新增了一批数据,同步数据库则会丢失这部分数据 二、实现思路 为了解决以上问题,保证原始数据库操作的每…...
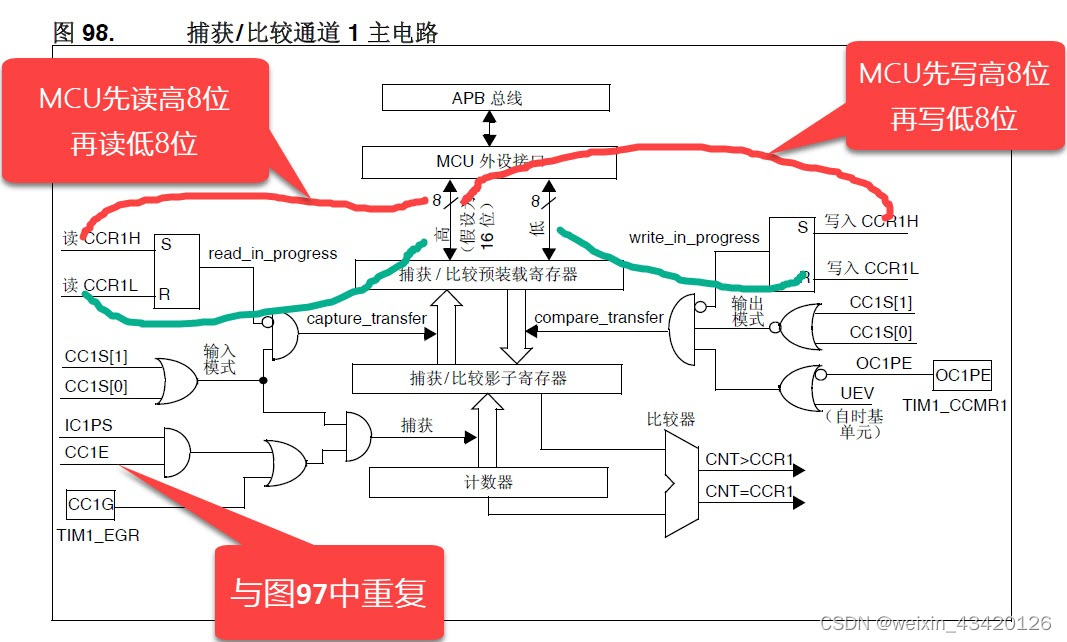
STM32F407-14.3.5-01捕获_比较通道
捕获/比较通道 每一个捕获/比较通道都是围绕着一个捕获/比较寄存器(包含影子寄存器) 包括: 捕获的输入部分(数字滤波、多路复用和预分频器), 输出部分(比较器和输出控制)。 中文参考手册中框图分成了三大模块, 把框图合并成了一个整体,以便更好的理解捕获输…...

【Python 训练营】N_12 打印菱形图案
题目 打印菱形图案 分析 先把图形分成两部分来看待,前四行一个规律,后三行一个规律,利用双重for循环,第一层控制行,第二层控制列。 答案 # 方法一 for i in range(4):block **(2*i1)print({:^7}.format(block))…...

risc-v异常处理
异常与中断的关系 中断和异常都为异常,分为: 同步异常:IO,illegal, page fault,miss_aligh 等来自处理器内部的发生的异常。异步异常(中断):鼠标,键盘,Time…...

SQL注入-数据库基础/SQL语法
目录 一,数据库概述 1.1 数据库 1.2 了解 ACID 理论 1.3 识别数据库 二,SQL 语法基础 三,SQL语句实例 3.1 SQL基础语句 3.2 SQL高级语句 四,基于SQL注入理解语法/函数 4.1 语法 4.2 函数 五,目录数据库info…...
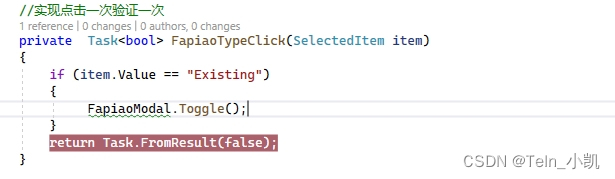
Blazor Select 实现点击一次选项触发一次后台事件
Blazor的官方案例中,Select组件只有两个事件 1、OnSelectedItemChanged 每次选项的时候改变触发,如果你点击同一个选项是不会触发后台的方法的 2、OnBeforeSelectedItemChange 我们可以用这个事件实现每次点击同一个选项都可以触发后台事件 需要注意下最…...
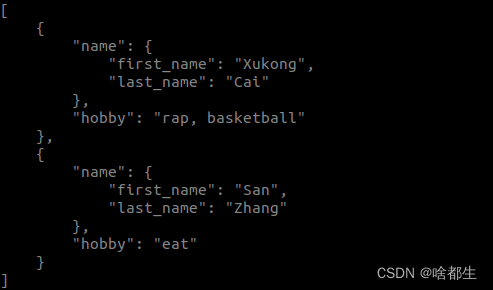
只会在终端使用Python运行代码?这些高级用法了解了解
大部分同学在终端使用Python可能只是简单的执行代码,但其实结合一些Python内置模块或第三方库可以实现更高级且便捷的用法,一起看看吧 插播,更多文字总结指南实用工具科技前沿动态第一时间更新在公粽号【啥都会一点的研究生】 代码Benchmar…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
